第1章 二次函数 单元精选精练(含解析)
文档属性
| 名称 | 第1章 二次函数 单元精选精练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 820.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-09 17:46:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第1章 二次函数 单元精选精练 2023-2024学年浙教版九年级数学上册 (含解析)
一、单选题
1.(2023秋·山东济南·九年级期末)若函数是二次函数,则m的值为( )
A.0或 B.0或1 C. D.1
2.(2023秋·河南·九年级校联考期末)关于抛物线,下列说法错误的是( )
A.对称轴是直线 B.最大值为
C.当时,随的增大而减小 D.与轴只有一个交点
3.(2023秋·安徽滁州·九年级校考期末)已知抛物线(为整数)与轴交于点,与轴交于点,且,则等于( )
A. B. C. D.
4.(2023秋·河北唐山·九年级统考期末)如图,二次函数的图像关于直线对称,与轴交于,两点,若,则下列四个结论:①,②,③,④.正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
5.(2023秋·江苏镇江·九年级统考期末)如图1,一张边长为、的长方形纸片的面积等于,将它通过割、拼,再补一个正方形,拼成一个新的正方形(如图2),可以取得的最小整数是( )
A. B. C. D.3
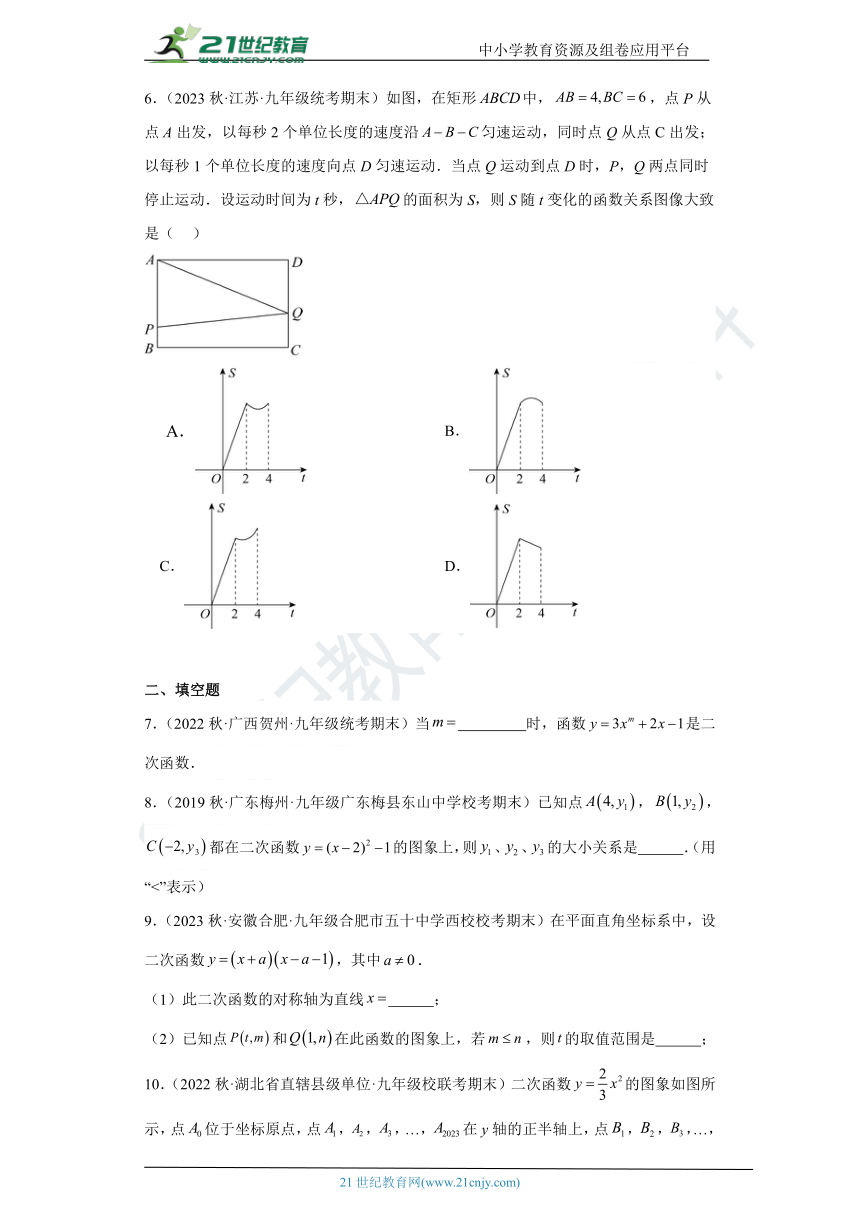
6.(2023秋·江苏·九年级统考期末)如图,在矩形中,,点P从点A出发,以每秒2个单位长度的速度沿匀速运动,同时点Q从点C出发;以每秒1个单位长度的速度向点D匀速运动.当点Q运动到点D时,P,Q两点同时停止运动.设运动时间为t秒,的面积为S,则S随t变化的函数关系图像大致是( )
B.
C. D.
二、填空题
7.(2022秋·广西贺州·九年级统考期末)当 时,函数是二次函数.
8.(2019秋·广东梅州·九年级广东梅县东山中学校考期末)已知点,,都在二次函数的图象上,则、、的大小关系是 .(用“<”表示)
9.(2023秋·安徽合肥·九年级合肥市五十中学西校校考期末)在平面直角坐标系中,设二次函数,其中.
(1)此二次函数的对称轴为直线 ;
(2)已知点和在此函数的图象上,若,则的取值范围是 ;
10.(2022秋·湖北省直辖县级单位·九年级校联考期末)二次函数的图象如图所示,点位于坐标原点,点,,,…,在y轴的正半轴上,点,,,…,在二次函数位于第一象限的图象上,若,,,…,都为等边三角形,则的边长为 .
三、解答题
11.(2023秋·宁夏石嘴山·九年级统考期末)在矩形中,,E是AB边上一动点,以1cm/s的速度从点B出发,到A停止运动;F是BC边上一动点,以2cm/s的速度从点B出发,到点C停止运动.设动点运动的时间为t(s),的面积为S(cm2)
(1)求S关于t的函数表达式,并求自变量t的取值范围.
(2)当△DEF是直角三角形时,求△DEF的面积.
12.(2023秋·安徽滁州·九年级校联考期末)设二次函数,的图像的顶点坐标分别为,.若,,且开口方向相同,则称是的“反倍顶二次函数”.
(1)请写出二次函数的“反倍顶二次函数”;
(2)已知关于的二次函数和二次函数.若函数恰是的“反倍顶二次函数”,求的值.
13.(2023秋·新疆和田·九年级统考期末)抛物线交x轴于点,交y轴于点.
(1)求抛物线的解析式,并直接写出抛物线的对称轴和另一个与x轴交点C的坐标;
(2)直接写出当时,x的取值范围.
(3)如图,点P是线段上方抛物线上一动点,当P点的坐标为_______时,的面积最大.
14.(2023秋·河南驻马店·九年级统考期末)距离寒假还有一个月的时候,严峻的疫情形势不得不让我们进行居家学习.虽然学习场所改变,从“面对面”转换到“屏对屏”,不变的是老师们的责任与爱心.某中学李老师每天从早晨开始准备一天的线上教学,直到晚上孩子熟睡,依然在书房认真批改线上作业,还不停和学生们进行线上答疑.为了方便线上教学,李老师使用一根60厘米长的铁丝制作一个“日”字形矩形框架(如图)当做手机的支架,铁丝恰好用完(接头长度忽略不计).
(1)若所围成的矩形框架的面积为144平方厘米,则的长为多少厘米?
(2)矩形框架面积的最大值为多少平方厘米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】利用二次函数定义可得,且,再解即可.
【详解】解:由题意得:,且,
解得:或且,
故,
故选:C.
【点睛】本题考查了二次函数的定义,一般地,我们把形如(其中a,b,c是常数,)的函数叫做二次函数,其中a称为二次项系数,b为一次项系数,c为常数项.
2.D
【分析】根据二次函数的性质求解判断即可.
【详解】
是直线的对称轴,
故A正确,
最大值为,
故B正确,
抛物线单调递减,
故C正确,
,
函数与轴有两个交点,
故D错误.
故选:D.
【点睛】本题考查二次函数的性质,解题关键是掌握二次函数与系数的关系.
3.D
【分析】当时,可求得为,由可得为或,将的坐标代入,进行计算即可得到答案.
【详解】解:当时,,
抛物线与轴的交点为,
,
抛物线与轴的交点为或,
或,
或,
或或或,
解得:或或,
为整数,
,
故选:D.
【点睛】本题主要考查了二次函数的图象与性质,二次函数与轴、轴的交点坐标,熟练掌握二次函数的图象与性质是解题的关键.
4.C
【分析】根据二次函数的对称性即可判断①;由开口方向和对称轴即可判断②;根据抛物线与x轴的交点有两个即可判断③;根据抛物线的开口方向、对称轴,与y轴的交点即可判断④.
【详解】解:∵对称轴为直线,,
∴,①正确,
∵ = 1,
∴,
∴,
∵,
∴,②正确;
∵抛物线与x轴有两个交点,
∴,③正确;
∵抛物线开口向上,与y轴的交点在x轴下方,
∴,
∴,即④错误.
故选C.
【点睛】本题主要考查图像与二次函数系数之间的关系、二次函数图像的性质等知识点,掌握数形结合思想以及二次函数图像与系数的关系是解答本题的关键.
5.B
【分析】利用长方形的面积公式,可得出关于的函数关系式,再利用二次函数的性质,即可解决最值问题.
【详解】解:根据题意得:,
,
.
,且,
当时,随的增大而增大,
当时,可以取得最小整数,此时.
故选:B.
【点睛】本题考查了二次函数的性质以及二次函数的最值,根据各数量之间的关系,找出k关于a的函数关系式是解题的关键.
6.A
【分析】根据题意当时,当时,分别求得的面积,即可判断函数图象.
【详解】解:依题意,时,,
,图象为直线的一部分,
∵,点运动时间为秒
当时,点在上,如图所示,
∴,,,,
∴
函数图象为开口向上的抛物线的一部分,
故选:A.
【点睛】本题考查了一次函数图象、二次函数图象的性质,根据题意求得解析式是解题的关键.
7.2
【分析】根据二次函数的定义计算即可.
【详解】∵函数是二次函数,
∴m=2,
故答案为:2.
【点睛】本题考查了二次函数的定义即形如,熟练掌握定义是解题的关键.
8.
【分析】先利用顶点式得到抛物线对称轴为直线,再比较点到直线的距离,然后根据二次函数的性质判断函数值的大小.
【详解】解:二次函数的图象的对称轴为直线,
因为点到直线的距离最小,点到直线的距离最大,且抛物线的开口向上,
所以.
故答案为.
【点睛】本题考查了二次函数的图象和性质,对于二次函数(a,b,c为常数,),当时,开口向上,在对称轴的左侧y随x的增大而减小,在对称轴的右侧y随x的增大而增大;当时,开口向下,在对称轴的左侧y随x的增大而增大,在对称轴的右侧y随x的增大而减小.
9. /0.5
【分析】(1)根据二次函数,经过和,是对称点,算出对称轴即可;
(2)根据对称轴为直线,点和在二次函数的图象上,画出函数图象,点关于对称轴的对称点,分析图象,写出的取值范围即可.
【详解】(1)二次函数,
函数经过和,是对称点,
对称轴为直线,
故答案为:
(2)二次函数,
二次项系数为,
函数图象开口向上,
又和在此函数的图象上,对称轴为直线,
画出图象如下图,点关于对称轴的对称点横坐标,
,
点应在线段下方部分的抛物线上(包括点、),
,
故答案为:
【点睛】本题考查了二次函数的图象和性质,画出图象数形结合是解题的关键.
10.2023
【分析】分别过点,,作y轴的垂线,垂足分别为A、B、C,设,,,则,,,再根据正三角形的边长,分别表示,,的纵坐标,逐步代入抛物线中,求a、b、c的值,得出规律.
【详解】分别过点,,作y轴的垂线,垂足分别为A、B、C,
设,,,
由勾股定理则,,,
在中,,
代入中,得,解得,即,
在中,,
代入中,得,解得,即,
在中,,
代入中,得,解得,即,
…,
以此类推由此可得的边长为2023.
故答案为:2023.
【点睛】本题考查了二次函数的综合运用,勾股定理应用,解题关键是根据正三角形的性质用边长表示抛物线上点的坐标,利用抛物线解析式求正三角形的边长.
11.(1)
(2)或
【分析】(1)先求出,再根据解答即可;
(2)先求出,,,再分①当为直角时,②当为直角时,③当为直角时三种情况讨论,应用勾股定理求出t的值,即可得答案.
【详解】(1)解:,
,
,
根据题意得
,
解得:;
(2)由勾股定理可得,
,
,
,
①当为直角时,,
即
解得,
;
②当为直角时,,
即,
解得或,
,
都不符合;
③当为直角时,,
即,
解得(舍)或,
.
【点睛】本题考查了函数关系式,解题的关键是找到.
12.(1)
(2)
【分析】(1)根据“反倍顶二次函数”的定义,求出顶点坐标即可解决问题;
(2)根据“反倍顶二次函数”的定义,列出方程即可解决问题.
【详解】(1)解:,
二次函数的顶点坐标为,
二次函数的一个“反倍顶二次函数”的顶点坐标为,
这个“反倍顶二次函数”的解析式为;
(2),顶点坐标为,
,顶点坐标为,
函数恰好是的“反倍顶二次函数”,
,
解得.
【点睛】本题考查二次函数的应用,解题的关键是理解题意,熟练掌握配方法确定顶点坐标是解题的基础,属于中考常考题型.
13.(1);;对称轴直线
(2)或
(3)
【分析】(1)用待定系数法求函数的解析式即可;
(2)根据函数图象即可得出结论;
(3)过点作轴交于点,设,则,则,再由此求解即可.
【详解】(1)将点,代入,
,
解得,
;
令,得
解得:
∴,
对称轴直线
(2)由(1)得:,
∴当或时,
(3)设直线的解析式为,
,
解得,
,
过点作轴交于点,
设,则,
,
,
当时,的面积有最大值,
此时,.
故答案为:.
【点睛】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,胡不归求最短距离的方法是解题的关键.
14.(1)12厘米或18厘米
(2)150平方厘米
【分析】(1)设的长为x厘米,则的长为厘米,根据面积公式列出一元二次方程,解之即可;
(2)在(1)的基础上,列出二次函数,再利用二次函数的性质可得出结论.
【详解】(1)设的长为x厘米,则的长为厘米,由题意得:
,
解得,,
∴的长为12厘米或18厘米;
(2)设矩形框架的面积为S平方厘米,
由题意得,
即,
∵,
∴要使框架的面积最大,则,此时,最大为150平方厘米.
【点睛】此题考查的是二次函数在实际生活中的运用及求函数最值的方法.解题的关键是用一个未知数表示出长和宽,利用面积公式来列出函数表达式后再求其最值.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
第1章 二次函数 单元精选精练 2023-2024学年浙教版九年级数学上册 (含解析)
一、单选题
1.(2023秋·山东济南·九年级期末)若函数是二次函数,则m的值为( )
A.0或 B.0或1 C. D.1
2.(2023秋·河南·九年级校联考期末)关于抛物线,下列说法错误的是( )
A.对称轴是直线 B.最大值为
C.当时,随的增大而减小 D.与轴只有一个交点
3.(2023秋·安徽滁州·九年级校考期末)已知抛物线(为整数)与轴交于点,与轴交于点,且,则等于( )
A. B. C. D.
4.(2023秋·河北唐山·九年级统考期末)如图,二次函数的图像关于直线对称,与轴交于,两点,若,则下列四个结论:①,②,③,④.正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
5.(2023秋·江苏镇江·九年级统考期末)如图1,一张边长为、的长方形纸片的面积等于,将它通过割、拼,再补一个正方形,拼成一个新的正方形(如图2),可以取得的最小整数是( )
A. B. C. D.3
6.(2023秋·江苏·九年级统考期末)如图,在矩形中,,点P从点A出发,以每秒2个单位长度的速度沿匀速运动,同时点Q从点C出发;以每秒1个单位长度的速度向点D匀速运动.当点Q运动到点D时,P,Q两点同时停止运动.设运动时间为t秒,的面积为S,则S随t变化的函数关系图像大致是( )
B.
C. D.
二、填空题
7.(2022秋·广西贺州·九年级统考期末)当 时,函数是二次函数.
8.(2019秋·广东梅州·九年级广东梅县东山中学校考期末)已知点,,都在二次函数的图象上,则、、的大小关系是 .(用“<”表示)
9.(2023秋·安徽合肥·九年级合肥市五十中学西校校考期末)在平面直角坐标系中,设二次函数,其中.
(1)此二次函数的对称轴为直线 ;
(2)已知点和在此函数的图象上,若,则的取值范围是 ;
10.(2022秋·湖北省直辖县级单位·九年级校联考期末)二次函数的图象如图所示,点位于坐标原点,点,,,…,在y轴的正半轴上,点,,,…,在二次函数位于第一象限的图象上,若,,,…,都为等边三角形,则的边长为 .
三、解答题
11.(2023秋·宁夏石嘴山·九年级统考期末)在矩形中,,E是AB边上一动点,以1cm/s的速度从点B出发,到A停止运动;F是BC边上一动点,以2cm/s的速度从点B出发,到点C停止运动.设动点运动的时间为t(s),的面积为S(cm2)
(1)求S关于t的函数表达式,并求自变量t的取值范围.
(2)当△DEF是直角三角形时,求△DEF的面积.
12.(2023秋·安徽滁州·九年级校联考期末)设二次函数,的图像的顶点坐标分别为,.若,,且开口方向相同,则称是的“反倍顶二次函数”.
(1)请写出二次函数的“反倍顶二次函数”;
(2)已知关于的二次函数和二次函数.若函数恰是的“反倍顶二次函数”,求的值.
13.(2023秋·新疆和田·九年级统考期末)抛物线交x轴于点,交y轴于点.
(1)求抛物线的解析式,并直接写出抛物线的对称轴和另一个与x轴交点C的坐标;
(2)直接写出当时,x的取值范围.
(3)如图,点P是线段上方抛物线上一动点,当P点的坐标为_______时,的面积最大.
14.(2023秋·河南驻马店·九年级统考期末)距离寒假还有一个月的时候,严峻的疫情形势不得不让我们进行居家学习.虽然学习场所改变,从“面对面”转换到“屏对屏”,不变的是老师们的责任与爱心.某中学李老师每天从早晨开始准备一天的线上教学,直到晚上孩子熟睡,依然在书房认真批改线上作业,还不停和学生们进行线上答疑.为了方便线上教学,李老师使用一根60厘米长的铁丝制作一个“日”字形矩形框架(如图)当做手机的支架,铁丝恰好用完(接头长度忽略不计).
(1)若所围成的矩形框架的面积为144平方厘米,则的长为多少厘米?
(2)矩形框架面积的最大值为多少平方厘米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】利用二次函数定义可得,且,再解即可.
【详解】解:由题意得:,且,
解得:或且,
故,
故选:C.
【点睛】本题考查了二次函数的定义,一般地,我们把形如(其中a,b,c是常数,)的函数叫做二次函数,其中a称为二次项系数,b为一次项系数,c为常数项.
2.D
【分析】根据二次函数的性质求解判断即可.
【详解】
是直线的对称轴,
故A正确,
最大值为,
故B正确,
抛物线单调递减,
故C正确,
,
函数与轴有两个交点,
故D错误.
故选:D.
【点睛】本题考查二次函数的性质,解题关键是掌握二次函数与系数的关系.
3.D
【分析】当时,可求得为,由可得为或,将的坐标代入,进行计算即可得到答案.
【详解】解:当时,,
抛物线与轴的交点为,
,
抛物线与轴的交点为或,
或,
或,
或或或,
解得:或或,
为整数,
,
故选:D.
【点睛】本题主要考查了二次函数的图象与性质,二次函数与轴、轴的交点坐标,熟练掌握二次函数的图象与性质是解题的关键.
4.C
【分析】根据二次函数的对称性即可判断①;由开口方向和对称轴即可判断②;根据抛物线与x轴的交点有两个即可判断③;根据抛物线的开口方向、对称轴,与y轴的交点即可判断④.
【详解】解:∵对称轴为直线,,
∴,①正确,
∵ = 1,
∴,
∴,
∵,
∴,②正确;
∵抛物线与x轴有两个交点,
∴,③正确;
∵抛物线开口向上,与y轴的交点在x轴下方,
∴,
∴,即④错误.
故选C.
【点睛】本题主要考查图像与二次函数系数之间的关系、二次函数图像的性质等知识点,掌握数形结合思想以及二次函数图像与系数的关系是解答本题的关键.
5.B
【分析】利用长方形的面积公式,可得出关于的函数关系式,再利用二次函数的性质,即可解决最值问题.
【详解】解:根据题意得:,
,
.
,且,
当时,随的增大而增大,
当时,可以取得最小整数,此时.
故选:B.
【点睛】本题考查了二次函数的性质以及二次函数的最值,根据各数量之间的关系,找出k关于a的函数关系式是解题的关键.
6.A
【分析】根据题意当时,当时,分别求得的面积,即可判断函数图象.
【详解】解:依题意,时,,
,图象为直线的一部分,
∵,点运动时间为秒
当时,点在上,如图所示,
∴,,,,
∴
函数图象为开口向上的抛物线的一部分,
故选:A.
【点睛】本题考查了一次函数图象、二次函数图象的性质,根据题意求得解析式是解题的关键.
7.2
【分析】根据二次函数的定义计算即可.
【详解】∵函数是二次函数,
∴m=2,
故答案为:2.
【点睛】本题考查了二次函数的定义即形如,熟练掌握定义是解题的关键.
8.
【分析】先利用顶点式得到抛物线对称轴为直线,再比较点到直线的距离,然后根据二次函数的性质判断函数值的大小.
【详解】解:二次函数的图象的对称轴为直线,
因为点到直线的距离最小,点到直线的距离最大,且抛物线的开口向上,
所以.
故答案为.
【点睛】本题考查了二次函数的图象和性质,对于二次函数(a,b,c为常数,),当时,开口向上,在对称轴的左侧y随x的增大而减小,在对称轴的右侧y随x的增大而增大;当时,开口向下,在对称轴的左侧y随x的增大而增大,在对称轴的右侧y随x的增大而减小.
9. /0.5
【分析】(1)根据二次函数,经过和,是对称点,算出对称轴即可;
(2)根据对称轴为直线,点和在二次函数的图象上,画出函数图象,点关于对称轴的对称点,分析图象,写出的取值范围即可.
【详解】(1)二次函数,
函数经过和,是对称点,
对称轴为直线,
故答案为:
(2)二次函数,
二次项系数为,
函数图象开口向上,
又和在此函数的图象上,对称轴为直线,
画出图象如下图,点关于对称轴的对称点横坐标,
,
点应在线段下方部分的抛物线上(包括点、),
,
故答案为:
【点睛】本题考查了二次函数的图象和性质,画出图象数形结合是解题的关键.
10.2023
【分析】分别过点,,作y轴的垂线,垂足分别为A、B、C,设,,,则,,,再根据正三角形的边长,分别表示,,的纵坐标,逐步代入抛物线中,求a、b、c的值,得出规律.
【详解】分别过点,,作y轴的垂线,垂足分别为A、B、C,
设,,,
由勾股定理则,,,
在中,,
代入中,得,解得,即,
在中,,
代入中,得,解得,即,
在中,,
代入中,得,解得,即,
…,
以此类推由此可得的边长为2023.
故答案为:2023.
【点睛】本题考查了二次函数的综合运用,勾股定理应用,解题关键是根据正三角形的性质用边长表示抛物线上点的坐标,利用抛物线解析式求正三角形的边长.
11.(1)
(2)或
【分析】(1)先求出,再根据解答即可;
(2)先求出,,,再分①当为直角时,②当为直角时,③当为直角时三种情况讨论,应用勾股定理求出t的值,即可得答案.
【详解】(1)解:,
,
,
根据题意得
,
解得:;
(2)由勾股定理可得,
,
,
,
①当为直角时,,
即
解得,
;
②当为直角时,,
即,
解得或,
,
都不符合;
③当为直角时,,
即,
解得(舍)或,
.
【点睛】本题考查了函数关系式,解题的关键是找到.
12.(1)
(2)
【分析】(1)根据“反倍顶二次函数”的定义,求出顶点坐标即可解决问题;
(2)根据“反倍顶二次函数”的定义,列出方程即可解决问题.
【详解】(1)解:,
二次函数的顶点坐标为,
二次函数的一个“反倍顶二次函数”的顶点坐标为,
这个“反倍顶二次函数”的解析式为;
(2),顶点坐标为,
,顶点坐标为,
函数恰好是的“反倍顶二次函数”,
,
解得.
【点睛】本题考查二次函数的应用,解题的关键是理解题意,熟练掌握配方法确定顶点坐标是解题的基础,属于中考常考题型.
13.(1);;对称轴直线
(2)或
(3)
【分析】(1)用待定系数法求函数的解析式即可;
(2)根据函数图象即可得出结论;
(3)过点作轴交于点,设,则,则,再由此求解即可.
【详解】(1)将点,代入,
,
解得,
;
令,得
解得:
∴,
对称轴直线
(2)由(1)得:,
∴当或时,
(3)设直线的解析式为,
,
解得,
,
过点作轴交于点,
设,则,
,
,
当时,的面积有最大值,
此时,.
故答案为:.
【点睛】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,胡不归求最短距离的方法是解题的关键.
14.(1)12厘米或18厘米
(2)150平方厘米
【分析】(1)设的长为x厘米,则的长为厘米,根据面积公式列出一元二次方程,解之即可;
(2)在(1)的基础上,列出二次函数,再利用二次函数的性质可得出结论.
【详解】(1)设的长为x厘米,则的长为厘米,由题意得:
,
解得,,
∴的长为12厘米或18厘米;
(2)设矩形框架的面积为S平方厘米,
由题意得,
即,
∵,
∴要使框架的面积最大,则,此时,最大为150平方厘米.
【点睛】此题考查的是二次函数在实际生活中的运用及求函数最值的方法.解题的关键是用一个未知数表示出长和宽,利用面积公式来列出函数表达式后再求其最值.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
