第4章 相似三角形单元精选精练(含解析)
文档属性
| 名称 | 第4章 相似三角形单元精选精练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 903.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-09 17:49:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第4章 相似三角形 单元精选精练 2023-2024学年浙教版九年级数学上册 (含解析)
一、单选题
1.(2023秋·陕西咸阳·九年级统考期末)下列给出长度的四条线段中,是成比例线段的是( )
A.,,, B.,,, C.,,, D.,,,
2.(2023秋·河南驻马店·九年级统考期末)如图,已知,,那么的长等于( )
A.4 B.5 C.6 D.7
3.(2020秋·全国·九年级统考期末)如果,、分别对应、,且,那么下列等式一定成立的是( )
A. B.的面积:的面积
C.的度数:的度数 D.的周长:的周长
4.(2023秋·安徽滁州·九年级校考期末)如图,为线段上的一点,与交于点,,与交于点,交于点,则下列结论中错误的是( )
A. B.
C. D.
5.(2023秋·安徽六安·九年级统考期末)如图,已知,则的长是( )
A.2 B. C. D.4
6.(2023秋·山东济宁·九年级统考期末)下列说法不正确的是( )
A.所有的正五边形都相似 B.所有的正方形都相似
C.所有的正三角形都相似 D.所有的等腰三角形都相似
7.(2023秋·河北保定·九年级统考期末)下列关于位似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;
④位似图形上任意两点与位似中心的距离之比等于位似比.
其中正确命题的序号是( )
A.②③ B.①② C.③④ D.②③④
二、填空题
8.(2023秋·安徽合肥·九年级合肥市五十中学西校校考期末)若,则 .
9.(2023秋·山西大同·九年级统考期末)如图,在中,是的中点,是的中点,则的长为 .
10.(2023秋·四川乐山·九年级统考期末)如图,在中,是斜边上的高,于点.除自身外,图中与相似的三角形的个数是 .
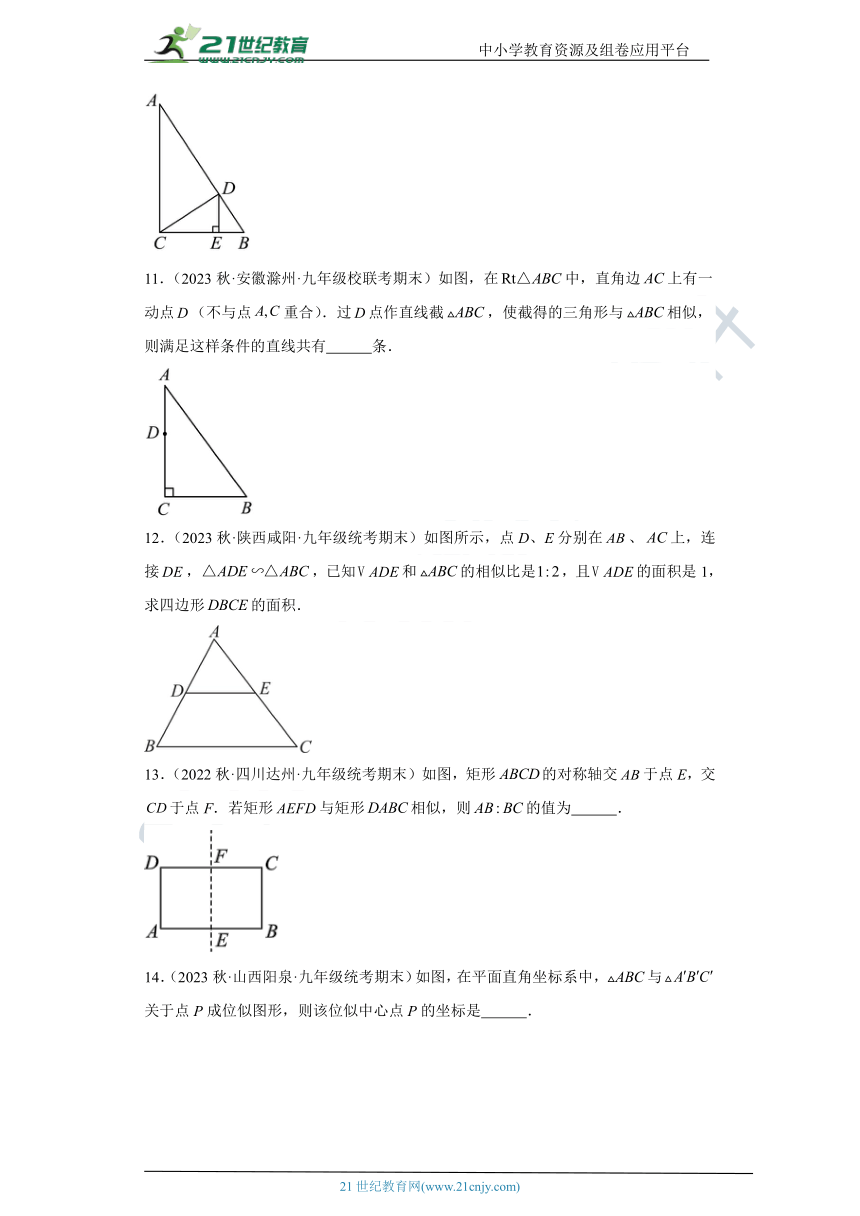
11.(2023秋·安徽滁州·九年级校联考期末)如图,在中,直角边上有一动点(不与点重合).过点作直线截,使截得的三角形与相似,则满足这样条件的直线共有 条.
12.(2023秋·陕西咸阳·九年级统考期末)如图所示,点D、E分别在、上,连接,,已知和的相似比是,且的面积是1,求四边形的面积.
13.(2022秋·四川达州·九年级统考期末)如图,矩形的对称轴交于点E,交于点F.若矩形与矩形相似,则的值为 .
14.(2023秋·山西阳泉·九年级统考期末)如图,在平面直角坐标系中,与关于点P成位似图形,则该位似中心点P的坐标是 .
三、解答题
15.(2022秋·安徽蚌埠·九年级校考期末)已知a,b,c为的三边长,且,.
(1)求线段a,b,c的长;
(2)若线段x是线段a,b的比例中顶(即),求线段x的长.
16.(2022秋·陕西渭南·九年级统考期末)如图,在中,,,若,求的长.
17.(2019秋·广东清远·九年级期末)如图,已知正方形中,平分且交边于点,将绕点顺时针旋转到的位置,并延长交于点.求证:
(1);
(2).
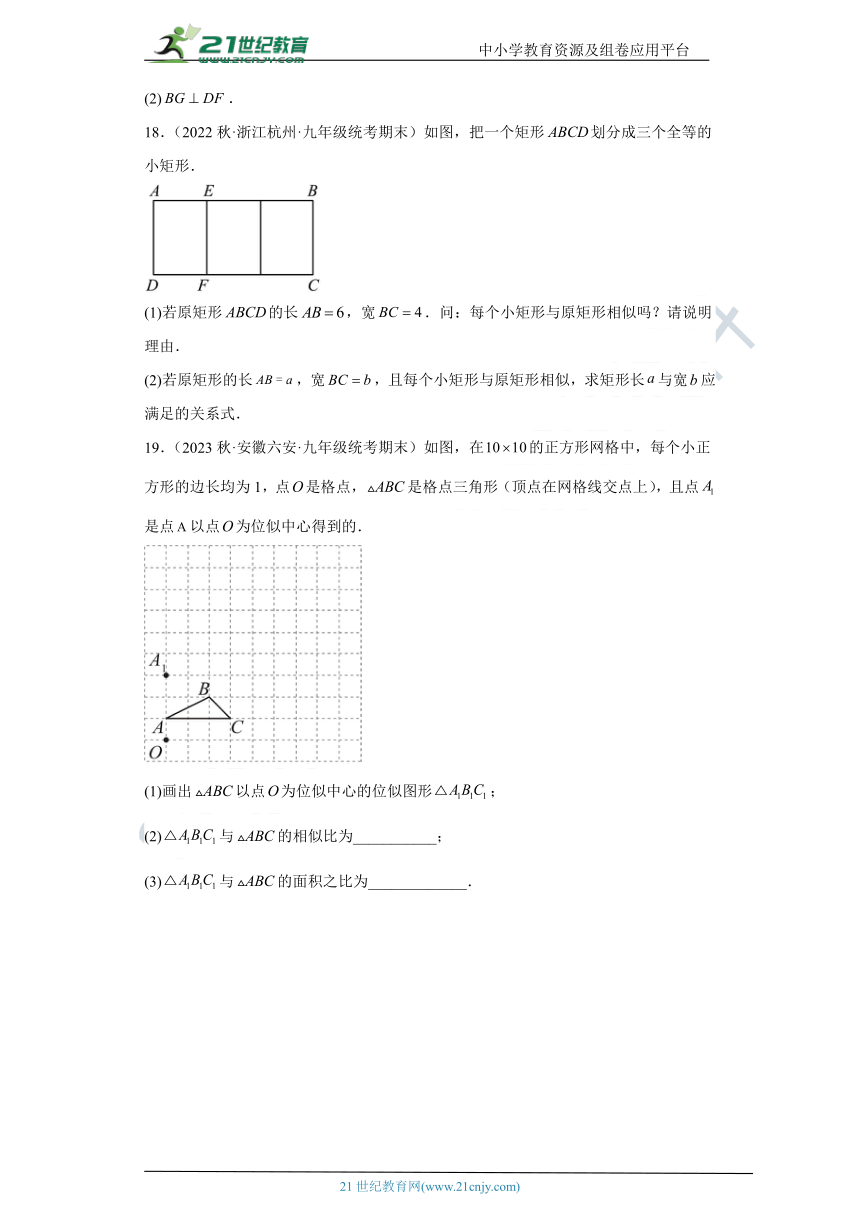
18.(2022秋·浙江杭州·九年级统考期末)如图,把一个矩形划分成三个全等的小矩形.
(1)若原矩形的长,宽.问:每个小矩形与原矩形相似吗?请说明理由.
(2)若原矩形的长,宽,且每个小矩形与原矩形相似,求矩形长与宽应满足的关系式.
19.(2023秋·安徽六安·九年级统考期末)如图,在的正方形网格中,每个小正方形的边长均为1,点是格点,是格点三角形(顶点在网格线交点上),且点是点以点为位似中心得到的.
(1)画出以点为位似中心的位似图形;
(2)与的相似比为___________;
(3)与的面积之比为_____________.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】根据比例线段的定义,分别计算各选项中最小的数与最大的数的积是否等于另外两个数的积可判断四条线段成比例.
【详解】、,此选项不符合题意,排除;
、,此选项不符合题意,排除;
、,此选项符合题意;
、,此选项不符合题意,排除;
故选:.
【点睛】此题考查了比例线段,解题的关键是如何判定四条线段是否成比例,只要把四条线段按大小顺序排列好,判断前两条线段之比与后两条线段之比是否相等即可,求线段之比时,要先统一线段的长度单位,最后的结果与所选取的单位无关系.
2.A
【分析】根据平行线分线段成比例得到,然后利用比例性质计算出,然后利用计算即可.
【详解】解:∵,
∴,即,
∴,
∴.
故选:A.
【点睛】本题考查了平行线分线段成比例,解题关键是熟练掌握三条平行线截两条直线,所得的对应线段成比例.
3.D
【分析】相似三角形对应边的比等于相似比,面积之比等于相似比的平方,对应角相等.
【详解】根据相似三角形性质可得:A:BC和DE不是对应边,故错;B:面积比应该是,故错;C:对应角相等,故错;D:周长比等于相似比,故正确.
故选:D
【点睛】考核知识点:相似三角形性质.理解基本性质是关键.
4.D
【分析】由相似三角形的判定逐一进行判断即可.
【详解】解:,且,
,
,故选项B正确,不符合题意;
,
,故选项A正确,不符合题意;
,
,故选项C正确,不符合题意;
由条件无法证明,故选项D错误,符合题意;
故选:D.
【点睛】本题考查了相似三角形的判定,熟练掌握相似三角形的判定是解题的关键.
5.B
【分析】通过证明,利用相似三角形的性质得出,进而得出答案.
【详解】解:∵,,
∴,
∴=,
∵,,
∴,
∴(负值已舍去).
故选:B.
【点睛】此题主要考查了相似三角形的判定和性质,正确得出对应边成比例的关系是解题关键.
6.D
【分析】相似形就是形状相同的两个图形,即对应边的比相等,对应角相等的两个图形,依据定义即可进行判断.
【详解】解:A.所有的正五边形都相似,正确,故此选项不符合题意;
B.所有的正方形都相似,正确,故此选项不符合题意;
C.所有的正三角形都相似,正确,故此选项不符合题意;
D.所有的等腰三角形对应边的比不一定相等,但对应角不一定相等,所有的等腰三角形不一定相似,故此选项符合题意.
故选:D.
【点睛】本题考查相似多边形的识别.解题的关键是掌握判定两个图形相似的依据:对应边的比相等,对应角相等,两个条件必须同时具备.
7.A
【分析】根据位似图形的性质和定义(识别位似图形,关键是看两个相似多边形的对应顶点所在的直线是否相交于一点,相交于一点的就是位似图形,交点就是位似中心)逐个判断即可得.
【详解】解:①相似图形不一定是位似图形,位似图形一定是相似图形,则原命题错误;
②位似图形一定有位似中心,则原命题正确;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形,则原命题正确;
④位似图形上任意一对对应点与位似中心的距离之比等于位似比,则原命题错误;
综上,正确命题的序号是②③,
故选:A.
【点睛】本题考查了位似图形的性质和概念,熟练掌握位似图形的性质是解题关键.
8.3
【分析】根据比例设,则,然后代入比例式进行计算即可.
【详解】解:,
设,则,,
.
故答案为:3.
【点睛】本题主要考查了比例的性质,掌握比的基本性质是解题的关键.
9.
【分析】如图,取的中点F,连接,由中位线定理得,由平行线分线段成比例定理,得,所以,得出结论.
【详解】解:如图,取的中点F,连接,
∵,
∴是的中位线,
∴,
∴,
∵,
∴,
∴,
∴,
故答案为:.
【点睛】本题考查中位线定理,平行线分线段成比例定理,添加辅助线,构造中位线是解题的关键.
10.
【分析】根据是斜边上的高,于点,得,,再根据相似三角形的判定,即可.
【详解】∵是斜边上的高,于点,
∴,,
在和中,
∵,
∴;
在和中,
∵,
∴;
∵,
∴,
∴;
∵,,
∴,
在和中,
,
∴;
∴图中与相似的三角形有个.
故答案为:.
【点睛】本题考查相似三角形的判定,解题的关键是掌握相似三角形的判定定理.
11.3
【分析】根据平行于三角形一边的直线截另两边或另两边的延长线所得三角形与原三角形相似,可以作,;又由有两个角对应相等的三角形相似,可以过点作于点.即可获得答案.
【详解】解:这样的直线有3条:
①如图1:作,∴;
②如图2:作,∴;
③如图3:过点作于点,
∴,
∵,
∴.
故答案为:3.
【点睛】此题主要考查了三角形相似的判定方法,解题关键是理解并掌握平行于三角形一边的直线截另两边或另两边的延长线所得三角形与原三角形相似,有两个角对应相等的三角形相似.
12.
【分析】利用相似三角形的性质求出的面积,可得结论.
【详解】解∶∵和的相似比是,
又∵的面积是1,
∴
【点睛】本题考查相似三角形的性质,解题关键是掌握相似三角形的性质,属于中考常考题型.
13.
【分析】根据相似多边形的对应边成比例进行计算即可解答.
【详解】解:∵四边形是矩形,
∴,
∵矩形的对称轴分别交于点E,交于点F,
∴,
∵矩形与矩形相似,
,
,
,
,
,
,
故答案为:.
【点睛】本题考查了矩形的性质,相似多边形的性质,轴对称的性质,熟练掌握相似多边形的对应边成比例是解题的关键.
14.
【分析】直接利用位似图形的性质得出位似中心位置即可.
【详解】解:如图所示:
位似中心点P的坐标是.
故答案为:.
【点睛】此题主要考查了位似变换,正确得出位似中心位置是解题关键.
15.(1)
(2)
【分析】(1)设,则,再结合题意可列出关于k的等式,解出k的值,即可求出线段a,b,c的长;
(2)由题意可直接得出,解出x的值(舍去负值)即可.
【详解】(1)由题意可设,则,
∵,
∴,
解得:,
∴;
(2)∵,
∴,
整理,得:,
解得:(舍去负值).
【点睛】本题考查比例的性质,比例中项的概念.利用“设k法”是解题关键.
16.
【分析】根据平行线的性质得出,结合已知条件证明,根据平行线分线段成比例即可求解.
【详解】,
,
,
,
,
,
,
,
解得:.
【点睛】本题考查了平行线的性质与判定,平行线分线段成比例,熟练掌握平行线分线段成比例是解题的关键.
17.(1)见解析
(2)见解析
【分析】(1)先判断出,再利用角平分线判断出,即可得出结论;
(2)由三角形的内角和定理可求,可得结论.
【详解】(1)证明:由旋转可知:,
.
平分,
,
,
,
;
(2)证明:,,
.
.
【点睛】本题考查了相似三角形的判定和性质,正方形的性质,旋转的性质,灵活运用这些性质解决问题是本题的关键.
18.(1)不相似;证明过程见详解
(2)
【分析】(1)根据划分后小矩形的长为,宽为,可得,进而可判断结论;
(2)根据划分后小矩形的长为,宽为,再根据每个小矩形与原矩形相似,可得,从而可得与的关系式.
【详解】(1)解:不相似.理由如下:
∵原矩形的长,宽,
∴划分后小矩形的长为,宽为,
又∵,即原矩形与每个小矩形的边不成比例,
∴每个小矩形与原矩形不相似.
(2)∵原矩形的长,宽,
∴划分后小矩形的长为,宽为,
又∵每个小矩形与原矩形相似,
∴
∴,即.
【点睛】本题考查了相似多边形的性质,本题的关键是根据两矩形相似得到比例式.
19.(1)见解析
(2)
(3)
【分析】(1)直接利用A点对应点位置结合位似中心得出B,C点对应点;
(2)利用所画图形,结合对应点与位似中心的距离得出位似比;
(3)得出三角形面积即可得出答案.
【详解】(1)解:如图所示,即为所求;
(2)解:∵由图可知,,
∴与的位似比为;
(3)解:∵,,
∴与的面积比为.
【点睛】此题主要考查了位似变换以及勾股定理,正确得出对应点位置是解题关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
第4章 相似三角形 单元精选精练 2023-2024学年浙教版九年级数学上册 (含解析)
一、单选题
1.(2023秋·陕西咸阳·九年级统考期末)下列给出长度的四条线段中,是成比例线段的是( )
A.,,, B.,,, C.,,, D.,,,
2.(2023秋·河南驻马店·九年级统考期末)如图,已知,,那么的长等于( )
A.4 B.5 C.6 D.7
3.(2020秋·全国·九年级统考期末)如果,、分别对应、,且,那么下列等式一定成立的是( )
A. B.的面积:的面积
C.的度数:的度数 D.的周长:的周长
4.(2023秋·安徽滁州·九年级校考期末)如图,为线段上的一点,与交于点,,与交于点,交于点,则下列结论中错误的是( )
A. B.
C. D.
5.(2023秋·安徽六安·九年级统考期末)如图,已知,则的长是( )
A.2 B. C. D.4
6.(2023秋·山东济宁·九年级统考期末)下列说法不正确的是( )
A.所有的正五边形都相似 B.所有的正方形都相似
C.所有的正三角形都相似 D.所有的等腰三角形都相似
7.(2023秋·河北保定·九年级统考期末)下列关于位似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;
④位似图形上任意两点与位似中心的距离之比等于位似比.
其中正确命题的序号是( )
A.②③ B.①② C.③④ D.②③④
二、填空题
8.(2023秋·安徽合肥·九年级合肥市五十中学西校校考期末)若,则 .
9.(2023秋·山西大同·九年级统考期末)如图,在中,是的中点,是的中点,则的长为 .
10.(2023秋·四川乐山·九年级统考期末)如图,在中,是斜边上的高,于点.除自身外,图中与相似的三角形的个数是 .
11.(2023秋·安徽滁州·九年级校联考期末)如图,在中,直角边上有一动点(不与点重合).过点作直线截,使截得的三角形与相似,则满足这样条件的直线共有 条.
12.(2023秋·陕西咸阳·九年级统考期末)如图所示,点D、E分别在、上,连接,,已知和的相似比是,且的面积是1,求四边形的面积.
13.(2022秋·四川达州·九年级统考期末)如图,矩形的对称轴交于点E,交于点F.若矩形与矩形相似,则的值为 .
14.(2023秋·山西阳泉·九年级统考期末)如图,在平面直角坐标系中,与关于点P成位似图形,则该位似中心点P的坐标是 .
三、解答题
15.(2022秋·安徽蚌埠·九年级校考期末)已知a,b,c为的三边长,且,.
(1)求线段a,b,c的长;
(2)若线段x是线段a,b的比例中顶(即),求线段x的长.
16.(2022秋·陕西渭南·九年级统考期末)如图,在中,,,若,求的长.
17.(2019秋·广东清远·九年级期末)如图,已知正方形中,平分且交边于点,将绕点顺时针旋转到的位置,并延长交于点.求证:
(1);
(2).
18.(2022秋·浙江杭州·九年级统考期末)如图,把一个矩形划分成三个全等的小矩形.
(1)若原矩形的长,宽.问:每个小矩形与原矩形相似吗?请说明理由.
(2)若原矩形的长,宽,且每个小矩形与原矩形相似,求矩形长与宽应满足的关系式.
19.(2023秋·安徽六安·九年级统考期末)如图,在的正方形网格中,每个小正方形的边长均为1,点是格点,是格点三角形(顶点在网格线交点上),且点是点以点为位似中心得到的.
(1)画出以点为位似中心的位似图形;
(2)与的相似比为___________;
(3)与的面积之比为_____________.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】根据比例线段的定义,分别计算各选项中最小的数与最大的数的积是否等于另外两个数的积可判断四条线段成比例.
【详解】、,此选项不符合题意,排除;
、,此选项不符合题意,排除;
、,此选项符合题意;
、,此选项不符合题意,排除;
故选:.
【点睛】此题考查了比例线段,解题的关键是如何判定四条线段是否成比例,只要把四条线段按大小顺序排列好,判断前两条线段之比与后两条线段之比是否相等即可,求线段之比时,要先统一线段的长度单位,最后的结果与所选取的单位无关系.
2.A
【分析】根据平行线分线段成比例得到,然后利用比例性质计算出,然后利用计算即可.
【详解】解:∵,
∴,即,
∴,
∴.
故选:A.
【点睛】本题考查了平行线分线段成比例,解题关键是熟练掌握三条平行线截两条直线,所得的对应线段成比例.
3.D
【分析】相似三角形对应边的比等于相似比,面积之比等于相似比的平方,对应角相等.
【详解】根据相似三角形性质可得:A:BC和DE不是对应边,故错;B:面积比应该是,故错;C:对应角相等,故错;D:周长比等于相似比,故正确.
故选:D
【点睛】考核知识点:相似三角形性质.理解基本性质是关键.
4.D
【分析】由相似三角形的判定逐一进行判断即可.
【详解】解:,且,
,
,故选项B正确,不符合题意;
,
,故选项A正确,不符合题意;
,
,故选项C正确,不符合题意;
由条件无法证明,故选项D错误,符合题意;
故选:D.
【点睛】本题考查了相似三角形的判定,熟练掌握相似三角形的判定是解题的关键.
5.B
【分析】通过证明,利用相似三角形的性质得出,进而得出答案.
【详解】解:∵,,
∴,
∴=,
∵,,
∴,
∴(负值已舍去).
故选:B.
【点睛】此题主要考查了相似三角形的判定和性质,正确得出对应边成比例的关系是解题关键.
6.D
【分析】相似形就是形状相同的两个图形,即对应边的比相等,对应角相等的两个图形,依据定义即可进行判断.
【详解】解:A.所有的正五边形都相似,正确,故此选项不符合题意;
B.所有的正方形都相似,正确,故此选项不符合题意;
C.所有的正三角形都相似,正确,故此选项不符合题意;
D.所有的等腰三角形对应边的比不一定相等,但对应角不一定相等,所有的等腰三角形不一定相似,故此选项符合题意.
故选:D.
【点睛】本题考查相似多边形的识别.解题的关键是掌握判定两个图形相似的依据:对应边的比相等,对应角相等,两个条件必须同时具备.
7.A
【分析】根据位似图形的性质和定义(识别位似图形,关键是看两个相似多边形的对应顶点所在的直线是否相交于一点,相交于一点的就是位似图形,交点就是位似中心)逐个判断即可得.
【详解】解:①相似图形不一定是位似图形,位似图形一定是相似图形,则原命题错误;
②位似图形一定有位似中心,则原命题正确;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形,则原命题正确;
④位似图形上任意一对对应点与位似中心的距离之比等于位似比,则原命题错误;
综上,正确命题的序号是②③,
故选:A.
【点睛】本题考查了位似图形的性质和概念,熟练掌握位似图形的性质是解题关键.
8.3
【分析】根据比例设,则,然后代入比例式进行计算即可.
【详解】解:,
设,则,,
.
故答案为:3.
【点睛】本题主要考查了比例的性质,掌握比的基本性质是解题的关键.
9.
【分析】如图,取的中点F,连接,由中位线定理得,由平行线分线段成比例定理,得,所以,得出结论.
【详解】解:如图,取的中点F,连接,
∵,
∴是的中位线,
∴,
∴,
∵,
∴,
∴,
∴,
故答案为:.
【点睛】本题考查中位线定理,平行线分线段成比例定理,添加辅助线,构造中位线是解题的关键.
10.
【分析】根据是斜边上的高,于点,得,,再根据相似三角形的判定,即可.
【详解】∵是斜边上的高,于点,
∴,,
在和中,
∵,
∴;
在和中,
∵,
∴;
∵,
∴,
∴;
∵,,
∴,
在和中,
,
∴;
∴图中与相似的三角形有个.
故答案为:.
【点睛】本题考查相似三角形的判定,解题的关键是掌握相似三角形的判定定理.
11.3
【分析】根据平行于三角形一边的直线截另两边或另两边的延长线所得三角形与原三角形相似,可以作,;又由有两个角对应相等的三角形相似,可以过点作于点.即可获得答案.
【详解】解:这样的直线有3条:
①如图1:作,∴;
②如图2:作,∴;
③如图3:过点作于点,
∴,
∵,
∴.
故答案为:3.
【点睛】此题主要考查了三角形相似的判定方法,解题关键是理解并掌握平行于三角形一边的直线截另两边或另两边的延长线所得三角形与原三角形相似,有两个角对应相等的三角形相似.
12.
【分析】利用相似三角形的性质求出的面积,可得结论.
【详解】解∶∵和的相似比是,
又∵的面积是1,
∴
【点睛】本题考查相似三角形的性质,解题关键是掌握相似三角形的性质,属于中考常考题型.
13.
【分析】根据相似多边形的对应边成比例进行计算即可解答.
【详解】解:∵四边形是矩形,
∴,
∵矩形的对称轴分别交于点E,交于点F,
∴,
∵矩形与矩形相似,
,
,
,
,
,
,
故答案为:.
【点睛】本题考查了矩形的性质,相似多边形的性质,轴对称的性质,熟练掌握相似多边形的对应边成比例是解题的关键.
14.
【分析】直接利用位似图形的性质得出位似中心位置即可.
【详解】解:如图所示:
位似中心点P的坐标是.
故答案为:.
【点睛】此题主要考查了位似变换,正确得出位似中心位置是解题关键.
15.(1)
(2)
【分析】(1)设,则,再结合题意可列出关于k的等式,解出k的值,即可求出线段a,b,c的长;
(2)由题意可直接得出,解出x的值(舍去负值)即可.
【详解】(1)由题意可设,则,
∵,
∴,
解得:,
∴;
(2)∵,
∴,
整理,得:,
解得:(舍去负值).
【点睛】本题考查比例的性质,比例中项的概念.利用“设k法”是解题关键.
16.
【分析】根据平行线的性质得出,结合已知条件证明,根据平行线分线段成比例即可求解.
【详解】,
,
,
,
,
,
,
,
解得:.
【点睛】本题考查了平行线的性质与判定,平行线分线段成比例,熟练掌握平行线分线段成比例是解题的关键.
17.(1)见解析
(2)见解析
【分析】(1)先判断出,再利用角平分线判断出,即可得出结论;
(2)由三角形的内角和定理可求,可得结论.
【详解】(1)证明:由旋转可知:,
.
平分,
,
,
,
;
(2)证明:,,
.
.
【点睛】本题考查了相似三角形的判定和性质,正方形的性质,旋转的性质,灵活运用这些性质解决问题是本题的关键.
18.(1)不相似;证明过程见详解
(2)
【分析】(1)根据划分后小矩形的长为,宽为,可得,进而可判断结论;
(2)根据划分后小矩形的长为,宽为,再根据每个小矩形与原矩形相似,可得,从而可得与的关系式.
【详解】(1)解:不相似.理由如下:
∵原矩形的长,宽,
∴划分后小矩形的长为,宽为,
又∵,即原矩形与每个小矩形的边不成比例,
∴每个小矩形与原矩形不相似.
(2)∵原矩形的长,宽,
∴划分后小矩形的长为,宽为,
又∵每个小矩形与原矩形相似,
∴
∴,即.
【点睛】本题考查了相似多边形的性质,本题的关键是根据两矩形相似得到比例式.
19.(1)见解析
(2)
(3)
【分析】(1)直接利用A点对应点位置结合位似中心得出B,C点对应点;
(2)利用所画图形,结合对应点与位似中心的距离得出位似比;
(3)得出三角形面积即可得出答案.
【详解】(1)解:如图所示,即为所求;
(2)解:∵由图可知,,
∴与的位似比为;
(3)解:∵,,
∴与的面积比为.
【点睛】此题主要考查了位似变换以及勾股定理,正确得出对应点位置是解题关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
