浙教版数学八年级上册1.1.2 三角形的角平分线、中线与高线 课件(共32张PPT)
文档属性
| 名称 | 浙教版数学八年级上册1.1.2 三角形的角平分线、中线与高线 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 893.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-10 13:22:20 | ||
图片预览







文档简介
(共32张PPT)
1.1 认识三角形
第2课时 三角形的角平分线、中线与高线
1.了解三角形的高线、中线、角平分线的概念.
2.会利用量角器、刻度尺画三角形高线、中线、角平分线.
3.会利用三角形的高线、中线、角平分线的概念,解决有关角度、面积计算等问题.
学习目标
你还记得“过一点画已知直线的垂线”吗?
情景导入
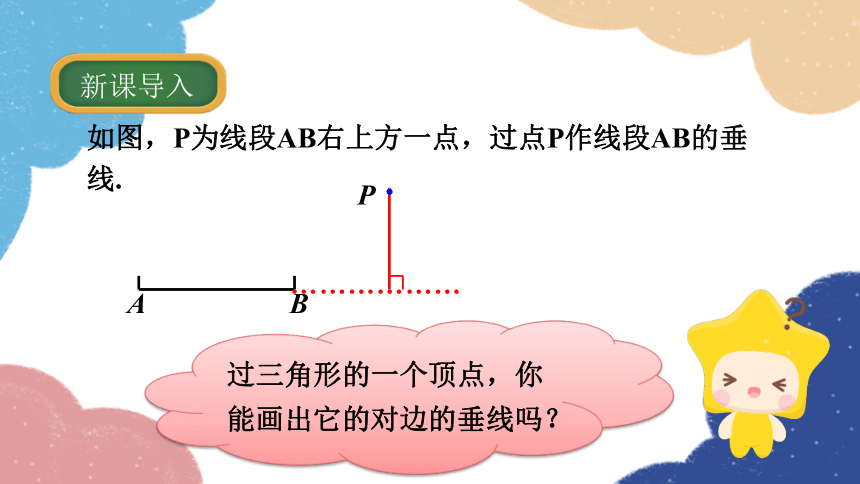
如图,P为线段AB右上方一点,过点P作线段AB的垂线.
A
B
………………
.
P
过三角形的一个顶点,你能画出它的对边的垂线吗?
新课导入
问题1:什么是三角形的高?怎样画三角形的高?
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线.
A
B
C
D
注意:标明垂直的记号和垂足的字母!
新课导入
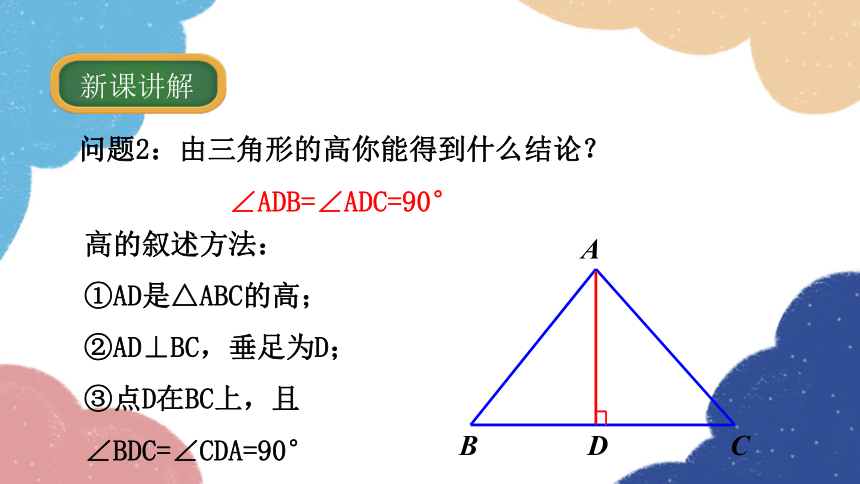
问题2:由三角形的高你能得到什么结论?
∠ADB=∠ADC=90°
高的叙述方法:
①AD是△ABC的高;
②AD⊥BC,垂足为D;
③点D在BC上,且∠BDC=∠CDA=90°
A
B
C
D
新课讲解
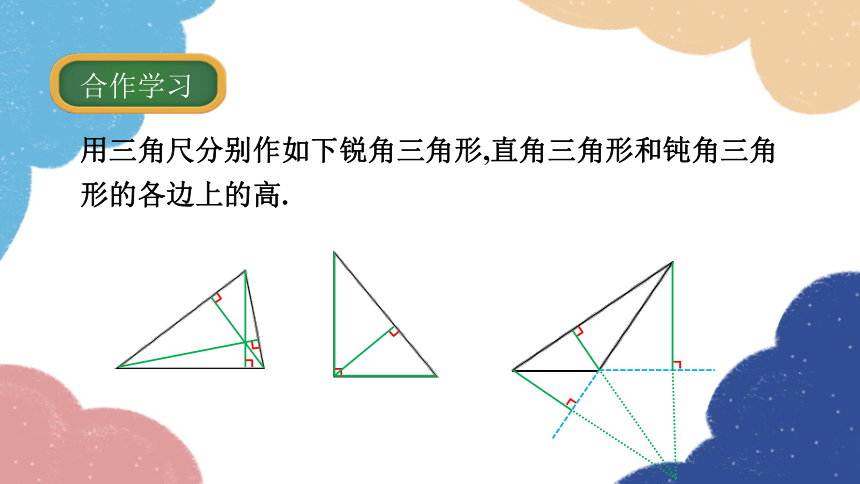
用三角尺分别作如下锐角三角形,直角三角形和钝角三角形的各边上的高.
合作学习
观察你所作的图形,比较三个三角形中三条高的位置,与三角形之间有什么关系
高 锐角三角形 直角三角形 钝角三角形
条数
位置
垂足
交点
3
3
3
都在三角形内部
直角边上的高分别与另一条直角边重合,还有一条高在三角形内部
夹钝角两边上的高在三角形外部,另一条高在内部
在相应顶点的对边上
①是直角的顶点
②在斜边上
①在相应顶点的对边的延长线上
②在钝角的对边上
在三角形内部
在直角顶点
在三角形外部
练一练
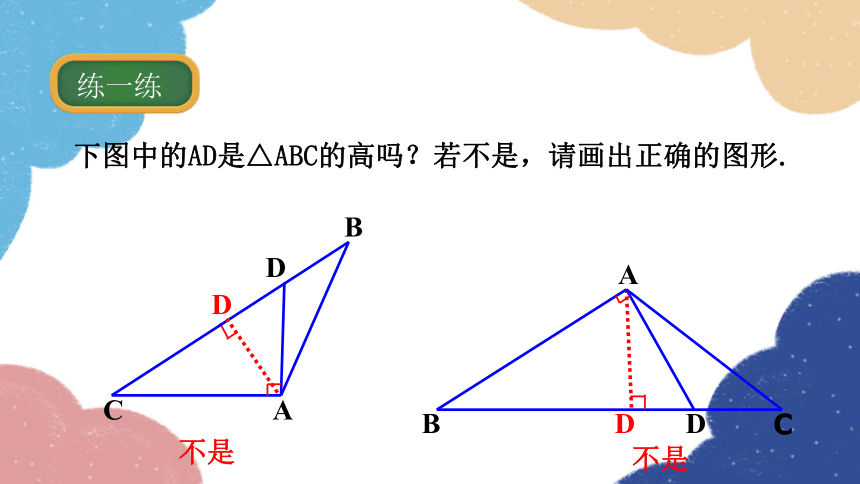
下图中的AD是△ABC的高吗?若不是,请画出正确的图形.
A
B
C
D
A
B
D
C
D
D
不是
不是
巩固练习
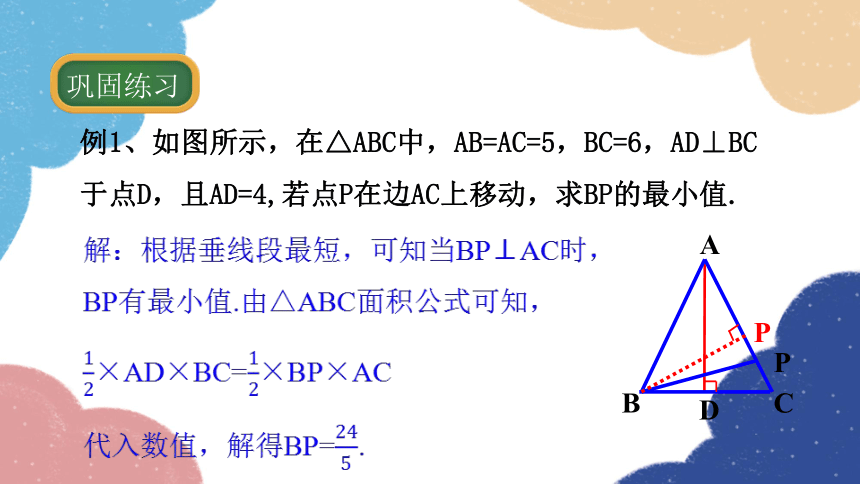
例1、如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,求BP的最小值.
A
C
B
D
P
P
方法总结
面积法的应用
若涉及两条高求长度,一般需结合面积(但不求出面积),利用三角形面积的两种不同表示方法列等式求解.
问题1:如图,如果点C是线段AB的中点,你能得到
什么结论?
A
B
C
新课讲解
问题2:如图,如果点D是线段BC的中点,那么线段AD就称为△ABC的中线.类比三角形的高的概念,试说明什么叫三角形的中线?
A
C
B
D
连结三角形的一个顶点与该顶点的对边中线的线段,叫做三角形的中线.
.
.
新课讲解
画一画
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
O
O
O
观察你所作的图形,思考一下它们中线的交点有什么规律?
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心.
三角形的中线能将三角形的面积平分.
问题3:如图,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?
A
C
B
D
E
答:相等,因为两个三角形等底同高,所以它们面积相等.
新课讲解
如图,点D,E,F 分别是△ABC的三条边的中点.设△ABC的面积为S,求△DEF的面积.
你可以这样考虑:
(1)连结AD. △ADC的面积是多少
(2)由第(1)题,你能求出△DEC的面积吗 △AEF和△FBD的面积呢
探究活动
A
B
C
E
F
D
问题1:如图,若OC是∠AOB的平分线,你能得到什么结论?
O
B
C
A
你能用同样的方法画出任意一个三角形的一个内角的平分线吗?
新课讲解
问题2:画出△ABC中∠A的平分线,试说明什么是三角形的角平分线?
A
C
B
新课讲解
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
想一想
三角形的角平分线与角的角平分线相同吗?
相同点:都是将一个角分成了两个相等的角.
不同点:前者是线段,后者是射线.
画一画
观察锐角三角形、直角三角形、钝角三角形的三条角平分线,你又发现了什么规律?
合作探究
1.锐角三角形
O
2.直角三角形
O
画一画
观察锐角三角形、直角三角形、钝角三角形的三条角平分线,你又发现了什么规律?
合作探究
3.钝角三角形
O
三角形的三条角平分线相交于一点,交点在三角形的内部.
练一练
如图,在ΔABC中,∠A=60°,∠ ABC、∠ ACB的平分线交于点O,则∠B0C的度数为__________ .
120°
巩固练习
例2、如图,在△ABC中,AD是△ABC的高线,AE是△ABC的角平分线.已知∠BAC=80°,∠C=40°.求∠DAE的大小.
A
C
B
D
E
提示:1.已知AE是△ABC的角平分线可以得到什么结论?
2.AD 是三角形的高,又可以得到什么结论
3.∠DAE可以看做哪两个角的差.
拓展创新
1、如下图,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B落在点B的位置,则线段AC( )
A.是边BB上的中线
B.是边BB上的高
C.是∠BAB的角平分线
D.具备以上三种性质
D
拓展创新
2、一个残缺的三角形残片如下图所示,请你作出AB边上的高所在的直线.你是怎样作的?为什么?
A
B
.
D
C
如果不恢复这个缺角呢?
拓展创新
┖
┛
┓
.
A
D
M
B
N
O
课堂小结
通过本节课的学习,你有哪些收获?
1.三角形的角平分线、中线与高线;
2.钝角三角形两短边上的高线的画法;
3.会利用三角形的中线性质,把原三角形的面积平分.
课下练习
数学趣味题:要栽7棵树,请你来帮忙,每行栽3棵,恰好成6行.(提示:排成三角形形状)
感谢观看!
1.1 认识三角形
第2课时 三角形的角平分线、中线与高线
1.了解三角形的高线、中线、角平分线的概念.
2.会利用量角器、刻度尺画三角形高线、中线、角平分线.
3.会利用三角形的高线、中线、角平分线的概念,解决有关角度、面积计算等问题.
学习目标
你还记得“过一点画已知直线的垂线”吗?
情景导入
如图,P为线段AB右上方一点,过点P作线段AB的垂线.
A
B
………………
.
P
过三角形的一个顶点,你能画出它的对边的垂线吗?
新课导入
问题1:什么是三角形的高?怎样画三角形的高?
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线.
A
B
C
D
注意:标明垂直的记号和垂足的字母!
新课导入
问题2:由三角形的高你能得到什么结论?
∠ADB=∠ADC=90°
高的叙述方法:
①AD是△ABC的高;
②AD⊥BC,垂足为D;
③点D在BC上,且∠BDC=∠CDA=90°
A
B
C
D
新课讲解
用三角尺分别作如下锐角三角形,直角三角形和钝角三角形的各边上的高.
合作学习
观察你所作的图形,比较三个三角形中三条高的位置,与三角形之间有什么关系
高 锐角三角形 直角三角形 钝角三角形
条数
位置
垂足
交点
3
3
3
都在三角形内部
直角边上的高分别与另一条直角边重合,还有一条高在三角形内部
夹钝角两边上的高在三角形外部,另一条高在内部
在相应顶点的对边上
①是直角的顶点
②在斜边上
①在相应顶点的对边的延长线上
②在钝角的对边上
在三角形内部
在直角顶点
在三角形外部
练一练
下图中的AD是△ABC的高吗?若不是,请画出正确的图形.
A
B
C
D
A
B
D
C
D
D
不是
不是
巩固练习
例1、如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,求BP的最小值.
A
C
B
D
P
P
方法总结
面积法的应用
若涉及两条高求长度,一般需结合面积(但不求出面积),利用三角形面积的两种不同表示方法列等式求解.
问题1:如图,如果点C是线段AB的中点,你能得到
什么结论?
A
B
C
新课讲解
问题2:如图,如果点D是线段BC的中点,那么线段AD就称为△ABC的中线.类比三角形的高的概念,试说明什么叫三角形的中线?
A
C
B
D
连结三角形的一个顶点与该顶点的对边中线的线段,叫做三角形的中线.
.
.
新课讲解
画一画
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
O
O
O
观察你所作的图形,思考一下它们中线的交点有什么规律?
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心.
三角形的中线能将三角形的面积平分.
问题3:如图,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?
A
C
B
D
E
答:相等,因为两个三角形等底同高,所以它们面积相等.
新课讲解
如图,点D,E,F 分别是△ABC的三条边的中点.设△ABC的面积为S,求△DEF的面积.
你可以这样考虑:
(1)连结AD. △ADC的面积是多少
(2)由第(1)题,你能求出△DEC的面积吗 △AEF和△FBD的面积呢
探究活动
A
B
C
E
F
D
问题1:如图,若OC是∠AOB的平分线,你能得到什么结论?
O
B
C
A
你能用同样的方法画出任意一个三角形的一个内角的平分线吗?
新课讲解
问题2:画出△ABC中∠A的平分线,试说明什么是三角形的角平分线?
A
C
B
新课讲解
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
想一想
三角形的角平分线与角的角平分线相同吗?
相同点:都是将一个角分成了两个相等的角.
不同点:前者是线段,后者是射线.
画一画
观察锐角三角形、直角三角形、钝角三角形的三条角平分线,你又发现了什么规律?
合作探究
1.锐角三角形
O
2.直角三角形
O
画一画
观察锐角三角形、直角三角形、钝角三角形的三条角平分线,你又发现了什么规律?
合作探究
3.钝角三角形
O
三角形的三条角平分线相交于一点,交点在三角形的内部.
练一练
如图,在ΔABC中,∠A=60°,∠ ABC、∠ ACB的平分线交于点O,则∠B0C的度数为__________ .
120°
巩固练习
例2、如图,在△ABC中,AD是△ABC的高线,AE是△ABC的角平分线.已知∠BAC=80°,∠C=40°.求∠DAE的大小.
A
C
B
D
E
提示:1.已知AE是△ABC的角平分线可以得到什么结论?
2.AD 是三角形的高,又可以得到什么结论
3.∠DAE可以看做哪两个角的差.
拓展创新
1、如下图,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B落在点B的位置,则线段AC( )
A.是边BB上的中线
B.是边BB上的高
C.是∠BAB的角平分线
D.具备以上三种性质
D
拓展创新
2、一个残缺的三角形残片如下图所示,请你作出AB边上的高所在的直线.你是怎样作的?为什么?
A
B
.
D
C
如果不恢复这个缺角呢?
拓展创新
┖
┛
┓
.
A
D
M
B
N
O
课堂小结
通过本节课的学习,你有哪些收获?
1.三角形的角平分线、中线与高线;
2.钝角三角形两短边上的高线的画法;
3.会利用三角形的中线性质,把原三角形的面积平分.
课下练习
数学趣味题:要栽7棵树,请你来帮忙,每行栽3棵,恰好成6行.(提示:排成三角形形状)
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
