浙教版数学八年级上册 1.5全等三角形的判定 角角边与角平分线的性质(第4课时)课件 21张PPT
文档属性
| 名称 | 浙教版数学八年级上册 1.5全等三角形的判定 角角边与角平分线的性质(第4课时)课件 21张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 683.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-11 09:47:58 | ||
图片预览






文档简介
(共21张PPT)
第一章 三角形的初步认识
1.5 全等三角形的判定
第4课时 “角角边”与角平分线的性质
学习目标
探索并理解“角角边”判定方法;
会用“角角边”判定方法证明三角形全等;
掌握角平分线的性质定理,能用角平分线的性质定理解决问题.
温故知新
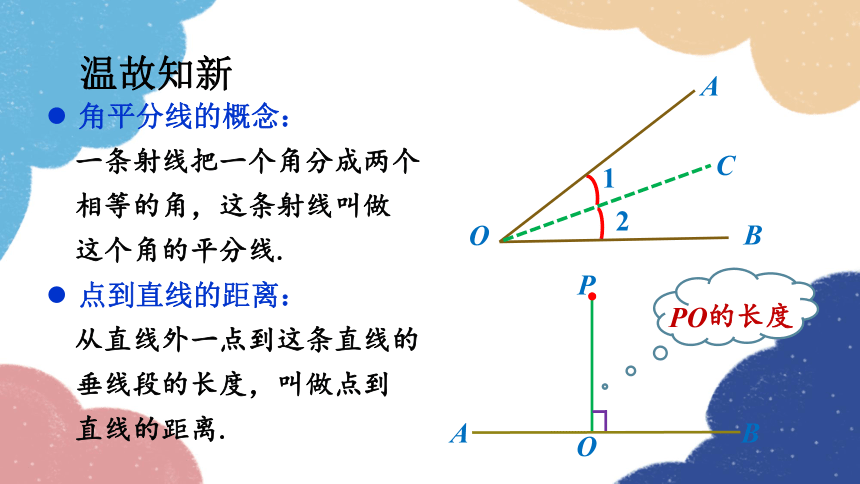
角平分线的概念:
一条射线把一个角分成两个
相等的角,这条射线叫做
这个角的平分线.
点到直线的距离:
从直线外一点到这条直线的
垂线段的长度,叫做点到
直线的距离.
C
O
B
A
1
2
O
P
A
B
PO的长度
温故知新
三角形全等的判定方法:
1.三边对应相等的两个三角形全等,
简写为“边边边”或“SSS”.
2.两边及其夹角对应相等的两个三角形全等,
简写为“边角边”或“SAS”.
3.两角及其夹边对应相等的两个三角形全等,
简写成“角边角”或“ASA”.
温故知新
1.三个角.
2.三条边.
3.两边一角.
4.两角一边
不能
SSS
当两个三角形满足六个条件中的三个时,有四种情况:
SAS
角—边—角
角—角—边
ASA
探究一:
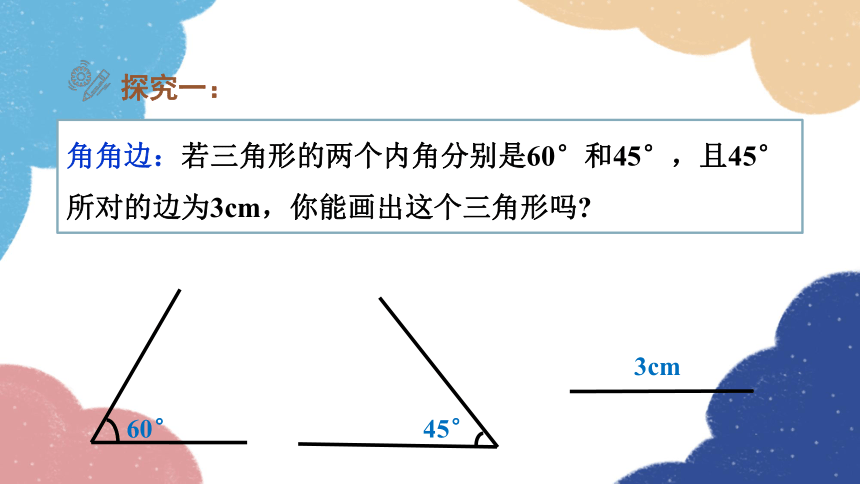
角角边:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
60°
45°
3cm
60°
探究一:
角角边:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
45°
45°
3cm
45°
两角及其中一个角的对边对应相等的两个三角形全等 . 简写成“角角边”或“AAS”.
角角边(AAS)
A
B
C
A′
B′
C′
几何语言:
在△ABC 和△A′B′C′中,
∴△ABC≌△A′B′C′(AAS).
∠A =∠A′,∠B =∠B,AC =A′C′,
典例讲解
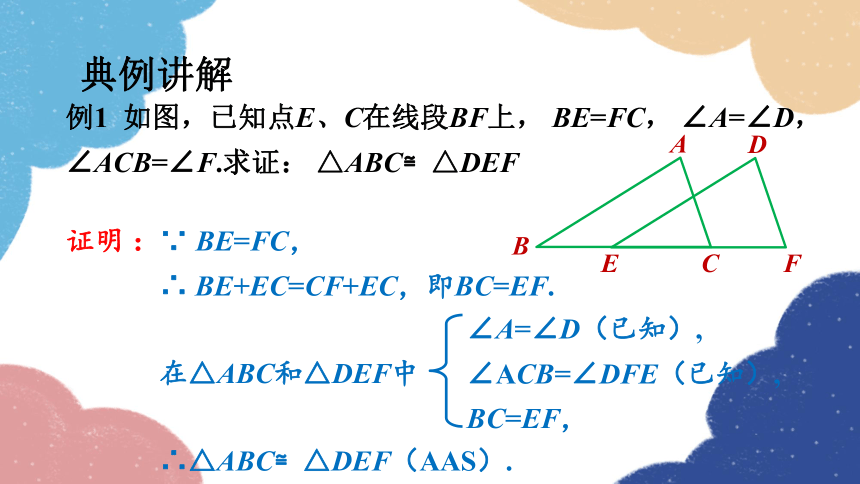
例1 如图,已知点E、C在线段BF上, BE=FC, ∠A=∠D,∠ACB=∠F.求证: △ABC≌△DEF
证明 :∵ BE=FC,
∴ BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中
∴△ABC≌△DEF(AAS).
A
B
C
D
E
F
∠A=∠D(已知),
∠ACB=∠DFE(已知),
BC=EF,
例2 已知:如图,P是∠AOB的平分线上的一点,PD⊥AO于点D,PC⊥BO于点C. 求证:PD=PC.
证明:∵PD⊥AO,PC⊥BO (已知),
∴∠PDO=∠PCO=90° (垂线的定义),
∠PDO=∠PCO,
∠POD=∠POC (角平分线的定义),
OP=OP,
∴PD=PC(全等三角形对应边相等).
在△OPD和△OPC中,
∴△OPD≌△OPC(AAS).
D
P
A
O
B
C
你能总结出角平分线的性质吗?
角平分线上的点到角两边的距离相等.
角平分线的性质定理
几何语言:
∵OC是∠AOB的平分线,
且PD⊥OA,PE⊥OB,
∴PD=PE.
E
D
O
A
B
P
C
典例讲解
例3 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,BD=2CD,点D到AB的距离为5.6cm,求BC的长.
解:过点D作DE⊥AB于点E.
∵∠C=90°,AD平分∠CAB(已知),
∴CD=DE=5.6cm.
(角平分线上的点到角两边的距离相等)
∴BD=2CD=2×5.6=11.2(cm).
∴BC=CD+BD=5.6+11.2=16.8(cm).
E
A
C
D
B
随堂练习
1.已知△ABC的六个元素如图所示,则甲、乙、丙三个三角形中与△ABC全等的图形是( )
A.甲、乙 B.乙、丙 C.只有乙 D.只有丙
解析:
甲图只有两个已知元素,不能确定与△ABC是否全等;
随堂练习
1.已知△ABC的六个元素如图所示,则甲、乙、丙三个三角形中与△ABC全等的图形是( )
A.甲、乙 B.乙、丙 C.只有乙 D.只有丙
解析:
乙图与△ABC满足“SAS”的条件,所以两个图形全等;
随堂练习
1.已知△ABC的六个元素如图所示,则甲、乙、丙三个三角形中与△ABC全等的图形是( )
A.甲、乙 B.乙、丙 C.只有乙 D.只有丙
解析:
丙图与△ABC满足“AAS”的条件,所以两个图形也全等.
B
2. 如图,已知∠1 = ∠2,∠C = ∠D.
求证: △ABC≌△ABD.
证明:在△ABC和△ABD中,
∠1 = ∠2,
∠C = ∠D,
AB = AB(公共边 ),
∴△ABC≌△ABD(AAS ),
∴AC = AD(全等三角形对应边相等)
A
B
D
C
2
1
3.如图,E,F 在线段AC上,AD∥CB,AE =CF.若∠B =
∠D,求证:DF =BE.
证明:∵AD∥CB ,∴∠A =∠C.
∵AE =CF ,∴AE-EF =CF-EF,即AF =CE.
∠A=∠C,
∠D=∠B(已知) ,
AF=CE ,
∴△ADF ≌△CBE(AAS).
∴DF =BE(全等三角形对应边相等).
在△ADF 和△CBE 中,
A
B
C
D
E
F
3. 如图,
已知:△ABC的外角∠CBD和∠BCE的平分线相交于点F.
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M,
∵点F在∠BCE的平分线上,
FG⊥AE, FM⊥BC,
G
H
M
A
B
D
C
E
F
∴FG=FM.
G
H
M
A
B
D
C
E
F
又∵点F在∠CBD平分线上,
FH⊥AD, FM⊥BC.
∴FM=FH.
∴FG=FH,
∴点F在∠DAE的平分线上.
3. 如图,
已知:△ABC的外角∠CBD和∠BCE的平分线相交于点F.
求证:点F在∠DAE的平分线上.
课堂小结
本章我们一共探索出判定三角形全等的四种方法,它们分别是:
1.边边边 (SSS)
3.角边角 (ASA)
4.角角边 (AAS)
2.边角边 (SAS)
角平分线的性质定理是:
角平分线上的点到角两边的距离相等.
感谢观看!
第一章 三角形的初步认识
1.5 全等三角形的判定
第4课时 “角角边”与角平分线的性质
学习目标
探索并理解“角角边”判定方法;
会用“角角边”判定方法证明三角形全等;
掌握角平分线的性质定理,能用角平分线的性质定理解决问题.
温故知新
角平分线的概念:
一条射线把一个角分成两个
相等的角,这条射线叫做
这个角的平分线.
点到直线的距离:
从直线外一点到这条直线的
垂线段的长度,叫做点到
直线的距离.
C
O
B
A
1
2
O
P
A
B
PO的长度
温故知新
三角形全等的判定方法:
1.三边对应相等的两个三角形全等,
简写为“边边边”或“SSS”.
2.两边及其夹角对应相等的两个三角形全等,
简写为“边角边”或“SAS”.
3.两角及其夹边对应相等的两个三角形全等,
简写成“角边角”或“ASA”.
温故知新
1.三个角.
2.三条边.
3.两边一角.
4.两角一边
不能
SSS
当两个三角形满足六个条件中的三个时,有四种情况:
SAS
角—边—角
角—角—边
ASA
探究一:
角角边:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
60°
45°
3cm
60°
探究一:
角角边:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
45°
45°
3cm
45°
两角及其中一个角的对边对应相等的两个三角形全等 . 简写成“角角边”或“AAS”.
角角边(AAS)
A
B
C
A′
B′
C′
几何语言:
在△ABC 和△A′B′C′中,
∴△ABC≌△A′B′C′(AAS).
∠A =∠A′,∠B =∠B,AC =A′C′,
典例讲解
例1 如图,已知点E、C在线段BF上, BE=FC, ∠A=∠D,∠ACB=∠F.求证: △ABC≌△DEF
证明 :∵ BE=FC,
∴ BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中
∴△ABC≌△DEF(AAS).
A
B
C
D
E
F
∠A=∠D(已知),
∠ACB=∠DFE(已知),
BC=EF,
例2 已知:如图,P是∠AOB的平分线上的一点,PD⊥AO于点D,PC⊥BO于点C. 求证:PD=PC.
证明:∵PD⊥AO,PC⊥BO (已知),
∴∠PDO=∠PCO=90° (垂线的定义),
∠PDO=∠PCO,
∠POD=∠POC (角平分线的定义),
OP=OP,
∴PD=PC(全等三角形对应边相等).
在△OPD和△OPC中,
∴△OPD≌△OPC(AAS).
D
P
A
O
B
C
你能总结出角平分线的性质吗?
角平分线上的点到角两边的距离相等.
角平分线的性质定理
几何语言:
∵OC是∠AOB的平分线,
且PD⊥OA,PE⊥OB,
∴PD=PE.
E
D
O
A
B
P
C
典例讲解
例3 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,BD=2CD,点D到AB的距离为5.6cm,求BC的长.
解:过点D作DE⊥AB于点E.
∵∠C=90°,AD平分∠CAB(已知),
∴CD=DE=5.6cm.
(角平分线上的点到角两边的距离相等)
∴BD=2CD=2×5.6=11.2(cm).
∴BC=CD+BD=5.6+11.2=16.8(cm).
E
A
C
D
B
随堂练习
1.已知△ABC的六个元素如图所示,则甲、乙、丙三个三角形中与△ABC全等的图形是( )
A.甲、乙 B.乙、丙 C.只有乙 D.只有丙
解析:
甲图只有两个已知元素,不能确定与△ABC是否全等;
随堂练习
1.已知△ABC的六个元素如图所示,则甲、乙、丙三个三角形中与△ABC全等的图形是( )
A.甲、乙 B.乙、丙 C.只有乙 D.只有丙
解析:
乙图与△ABC满足“SAS”的条件,所以两个图形全等;
随堂练习
1.已知△ABC的六个元素如图所示,则甲、乙、丙三个三角形中与△ABC全等的图形是( )
A.甲、乙 B.乙、丙 C.只有乙 D.只有丙
解析:
丙图与△ABC满足“AAS”的条件,所以两个图形也全等.
B
2. 如图,已知∠1 = ∠2,∠C = ∠D.
求证: △ABC≌△ABD.
证明:在△ABC和△ABD中,
∠1 = ∠2,
∠C = ∠D,
AB = AB(公共边 ),
∴△ABC≌△ABD(AAS ),
∴AC = AD(全等三角形对应边相等)
A
B
D
C
2
1
3.如图,E,F 在线段AC上,AD∥CB,AE =CF.若∠B =
∠D,求证:DF =BE.
证明:∵AD∥CB ,∴∠A =∠C.
∵AE =CF ,∴AE-EF =CF-EF,即AF =CE.
∠A=∠C,
∠D=∠B(已知) ,
AF=CE ,
∴△ADF ≌△CBE(AAS).
∴DF =BE(全等三角形对应边相等).
在△ADF 和△CBE 中,
A
B
C
D
E
F
3. 如图,
已知:△ABC的外角∠CBD和∠BCE的平分线相交于点F.
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M,
∵点F在∠BCE的平分线上,
FG⊥AE, FM⊥BC,
G
H
M
A
B
D
C
E
F
∴FG=FM.
G
H
M
A
B
D
C
E
F
又∵点F在∠CBD平分线上,
FH⊥AD, FM⊥BC.
∴FM=FH.
∴FG=FH,
∴点F在∠DAE的平分线上.
3. 如图,
已知:△ABC的外角∠CBD和∠BCE的平分线相交于点F.
求证:点F在∠DAE的平分线上.
课堂小结
本章我们一共探索出判定三角形全等的四种方法,它们分别是:
1.边边边 (SSS)
3.角边角 (ASA)
4.角角边 (AAS)
2.边角边 (SAS)
角平分线的性质定理是:
角平分线上的点到角两边的距离相等.
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
