相似三角形的性质及其应用1

课件16张PPT。平湖市福臻中学
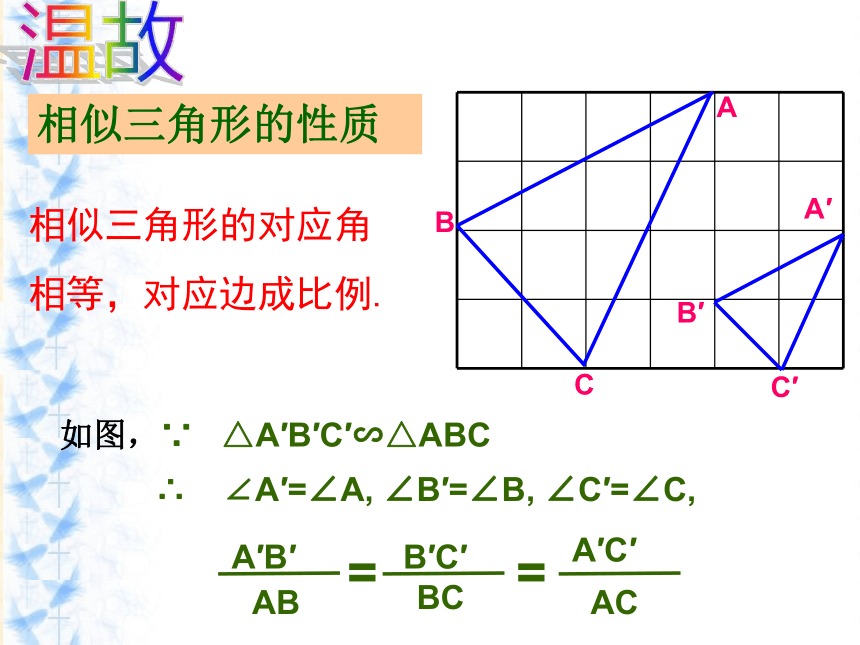
吴 燕4.1比例线段（三）4.5相似三角形性质及其应用（1）温故BAC相似三角形的对应角相等，对应边成比例.如图，∵ △A′B′C′∽△ABC∴ ∠A′=∠A, ∠B′=∠B, ∠C′=∠C,相似三角形的性质1、如图，△ABC∽△AED，
∠ADE=80°，∠A=60°，则∠C= .
(2)AD=1.5,DE=2,BC=4,则AC= .
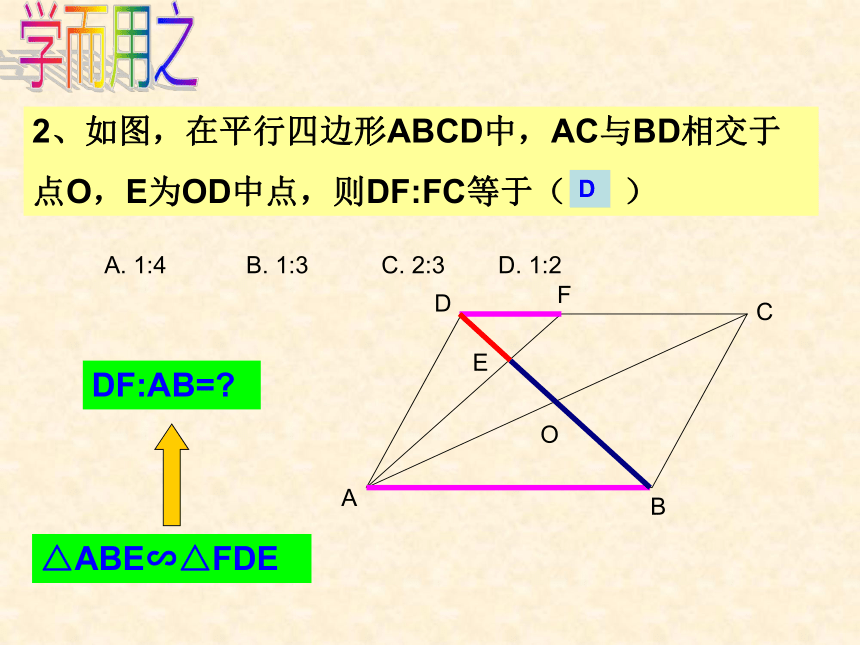
80°3学而用之2、如图，在平行四边形ABCD中，AC与BD相交于
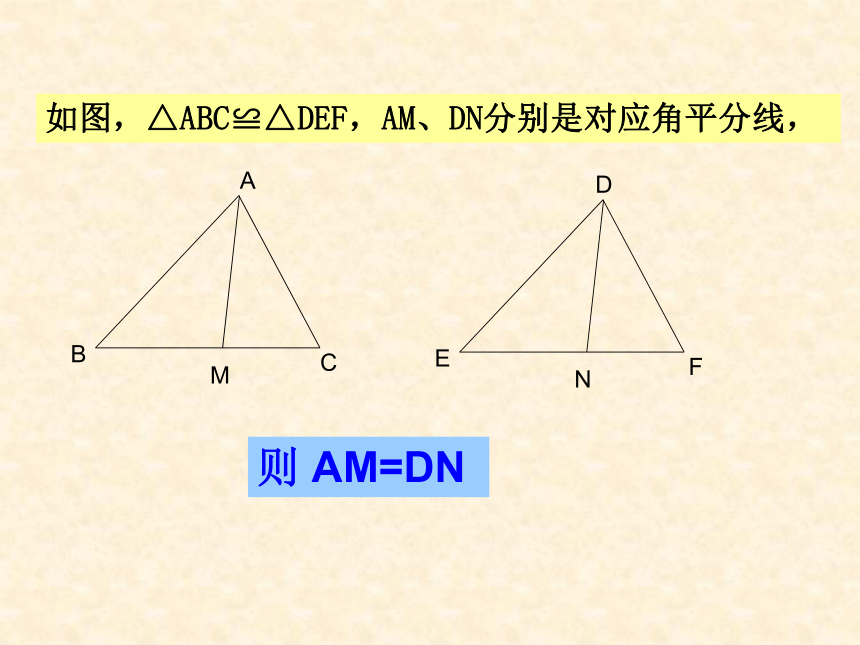
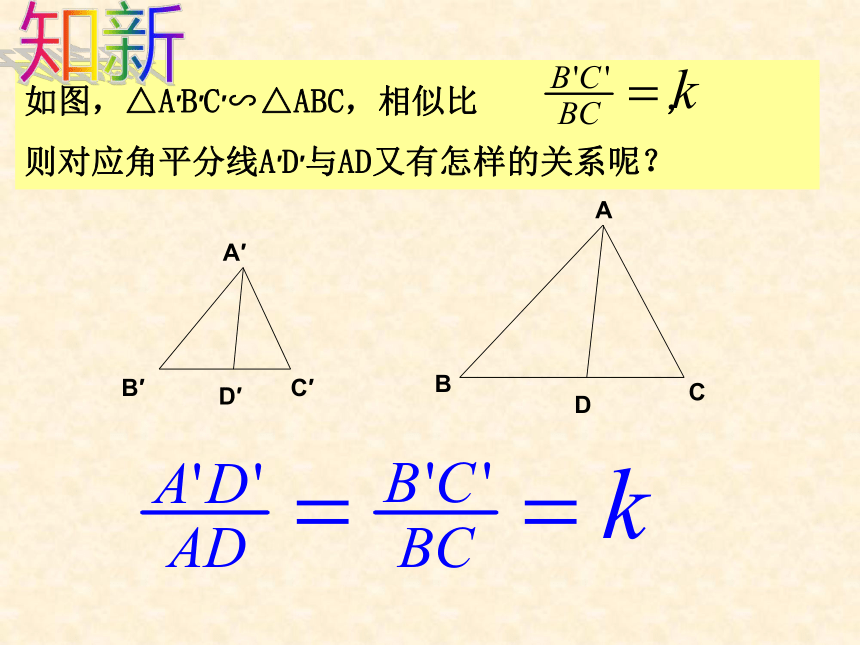
点O，E为OD中点，则DF:FC等于（ ） DA. 1:4 B. 1:3 C. 2:3 D. 1:2学而用之DF:AB=? 则 AM=DN如图，△ABC≌△DEF，AM、DN分别是对应角平分线，知新知新知新高线、中线知新三角形的重心定义三角形三条中线的交点叫做三角形的重心。三角形的重心性质三角形的重心分每一条中线成1:2的两条线段。知新1、如图，在△ABC中，点E、F分别是AC、AB的中点，BE、CF相交于点G，FG=1,则CF的长为（ ）CA. 2 B. 1.5 C. 3 D. 4学而用之学而用之ACBDEF3、如图，等边三角形ABC的边长为3，P为BC上一点，且BP=1，D为AC上一点，若∠APD=60°，则CD长为 . 学而用之24、如图，在△ABC中，中线AD，BE相交于点F，EG∥BC，交AD于点G，求AG与GF的比.学而用之三角形的重心三角形三条中线的交点叫做三角形的重心。性质:三角形的重心分每一条中线成1:2的两条线段。小结相似三角形的对应角相等，对应边成比例.相似三角形的性质:定义5．已知三角形ABC的边BC=8，高AD=16，矩形PQMN的四个顶点在三角形的边上，设QM为x，矩形PQMN的面积为S，求：
（1）S关于的函数关系式及自变量的取值范围
（2）当自变量取何值时，矩形面积最大？最大为多少?学而用之