浙教版数学八年级上册 4.2平面直角坐标系第1课时 平面直角坐标系课件(共22张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 4.2平面直角坐标系第1课时 平面直角坐标系课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-13 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
4.2 平面直角坐标系
第1课时 平面直角坐标系
学习目标
1.认识并能画出平面直角坐标系.
2.在给定的直角坐标系中,会根据坐标描出点的位置,能由点的位置写出它的坐标.
情境引入
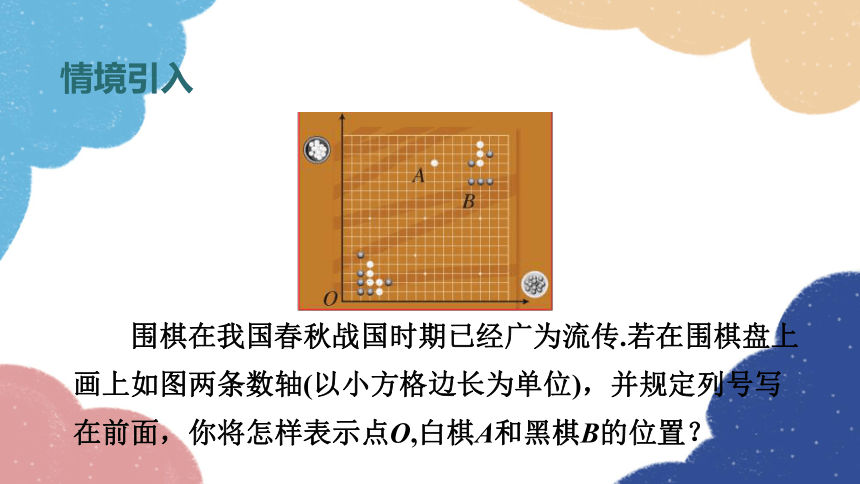
围棋在我国春秋战国时期已经广为流传.若在围棋盘上画上如图两条数轴(以小方格边长为单位),并规定列号写在前面,你将怎样表示点O,白棋A和黑棋B的位置?
合作探究
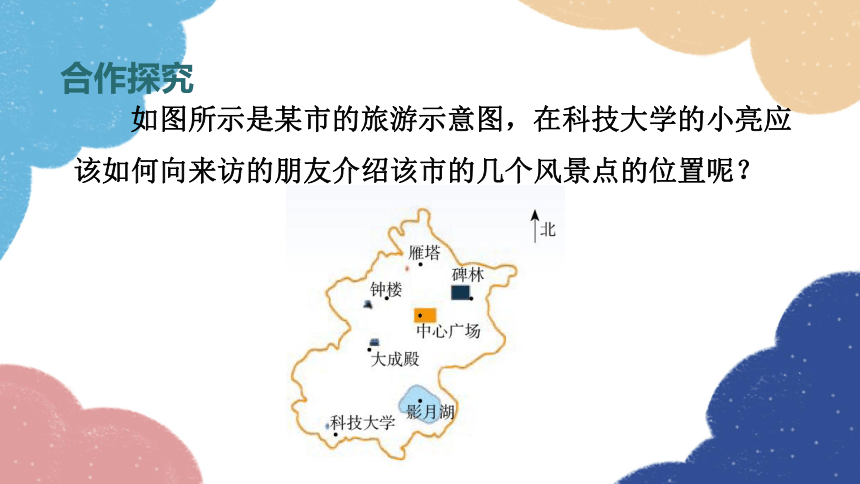
如图所示是某市的旅游示意图,在科技大学的小亮应该如何向来访的朋友介绍该市的几个风景点的位置呢?
探究一、小亮在旅游示意图上画上了方格,标上数字,并用(0,0)表示科技大学的位置,用(5,7)表示中心广场的位置,那么钟楼的位置如何表示?(2,5)表示哪个地点的位置?(5,2)呢?
解:(3,8)表示钟楼的位置;
(2,5)表示大成殿;
(5,2)表示影月湖.
探究二、 如果小亮和他的朋友在中心广场,并以中心广场为“原点”,做如图所示的标记,那么你能表示“碑林” 的位置吗?“大成殿”的位置呢?
解:碑林(3,1),
大成殿(-3,-2).
这种表示位置的方法是借助了平面直角坐标系,预习教材回答:什么是平面直角坐标系?
新知讲解
1.平面直角坐标系的概念
在平面内画两条互相垂直,并且有公共原点O的数轴.
O
其中一条叫做x轴,通常画成水平,另一条叫做y轴,画成与x轴垂直.
x
y
这样,就在平面内建立了平面直角坐标系,坐标系所在的平面叫做坐标平面,公共原点O叫做直角坐标系的原点.
特别提示
(1)两条数轴要互相垂直,且有公共原点.
(2)一般情况下,两条数轴一条水平,一条铅垂.
(3)表示数轴正方向的箭头一定要画,横轴箭头旁标上x,纵轴箭头旁标上y.一般地,x轴取向右的方向为正方向,y轴取向上的方向为正方向.
(4)一般情况下,两条数轴的单位长度是统一的.
2.点的坐标
O
x
y
对于平面内任意一点M,作MM1⊥x轴,MM2⊥y轴.
设垂足M1,M2在各自数轴上所表示的数分别是x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序实数对(x,y)叫做点M的坐标.
M
M1
M2
(x,y)
建立了平面直角坐标系后,对于坐标平面内任何一点,我们可以确定它的坐标.反过来,对于任何一个坐标,我们可以在坐标平面内确定它所表示的一个点.
坐标平面内的点的坐标有什么符号特征呢?
3.点的坐标的符号特征
x轴和y轴把坐标平面分成四个象限,如图所示.
象限以数轴为界,x轴,y轴上的点不属于任何象限.
O
x
y
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
-1
-2
-3
-4
第一象限
第二象限
第三象限
第四象限
小组讨论,总结出各个象限内点的坐标的符号特征.
O
x
y
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
-1
-2
-3
-4
第一象限
第二象限
第三象限
第四象限
象限 x,y的符号
第一象限
第二象限
第三象限
第四象限
点(x,y)
四个象限中点的坐标的符号特征如下表:
(+,+)
(-,+)
(-,-)
(+,-)
(+,+)
(-,+)
(-,-)
(+,-)
例题解答
例 (1)如图,写出平面直角坐标系内点M,N,L,O,P的坐标.
解:(1)所求各点坐标为:
M(2,4),N(-2,2),
L(0,-2.5),O(0,0),P(2,-2.5).
例 (2) 在平面直角坐标系内画出点A(2,4),B(5,2), C(-3.5,0),
D(-3.5,-2).
(2)A,B,C,D各点的位置如图:
A
B
C
D
A
B
C
D
思考:点(2,4)与点(4,2)是不是同一个点?
点(-2,4)与点(2,-4)呢?
解:在图中分别找出各点进行判断.
可以看出,所给点是四个不同的点.
(2,4)
(4,2)
(-2,4)
(2,-4)
表示点的坐标的两个数是有顺序的,当a≠b时,点P(a,b)与点Q(b,a)表示不同的点.
1.下面是平面直角坐标系的为( )
随堂练习
A.
B.
C.
D.
C
2.在平面直角坐标系中,已知点P(2,-3),则点P在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:∵横坐标为正,纵坐标为负,
∴点P(2,-3)在第四象限,∴选D.
D
3.若点P(m,1-2m) 横坐标与纵坐标互为相反数,
则点P一定在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
解析:∵点P(m,1-2m)的横坐标与纵坐标互为相反数,
∴m+1-2m=0, 解得m=1, ∴点P(1,-1),
∴点P一定在第四象限.
4.根据图中各点的位置填表.
点 坐标 所在象限
或坐标轴
A
B
C
D
E
F
G
O
(4,5)
(-5,4)
(-3,-5)
(3,0)
(5,-4)
(2.5,-2.5)
(0,5.5)
(0,0)
一
二
三
x轴
四
四
y轴
x轴,y轴
课堂小结
坐标平面内点的坐标特征
位置 坐标特征 图象
第一象限
第二象限
第三象限
第四象限
x轴 正半轴
负半轴
y轴 正半轴
负半轴
原点
(+,+)
(-,+)
(-,-)
(+,-)
(+,0)
(-,0)
(0,+)
(0,-)
(0,0)
感谢观看!
4.2 平面直角坐标系
第1课时 平面直角坐标系
学习目标
1.认识并能画出平面直角坐标系.
2.在给定的直角坐标系中,会根据坐标描出点的位置,能由点的位置写出它的坐标.
情境引入
围棋在我国春秋战国时期已经广为流传.若在围棋盘上画上如图两条数轴(以小方格边长为单位),并规定列号写在前面,你将怎样表示点O,白棋A和黑棋B的位置?
合作探究
如图所示是某市的旅游示意图,在科技大学的小亮应该如何向来访的朋友介绍该市的几个风景点的位置呢?
探究一、小亮在旅游示意图上画上了方格,标上数字,并用(0,0)表示科技大学的位置,用(5,7)表示中心广场的位置,那么钟楼的位置如何表示?(2,5)表示哪个地点的位置?(5,2)呢?
解:(3,8)表示钟楼的位置;
(2,5)表示大成殿;
(5,2)表示影月湖.
探究二、 如果小亮和他的朋友在中心广场,并以中心广场为“原点”,做如图所示的标记,那么你能表示“碑林” 的位置吗?“大成殿”的位置呢?
解:碑林(3,1),
大成殿(-3,-2).
这种表示位置的方法是借助了平面直角坐标系,预习教材回答:什么是平面直角坐标系?
新知讲解
1.平面直角坐标系的概念
在平面内画两条互相垂直,并且有公共原点O的数轴.
O
其中一条叫做x轴,通常画成水平,另一条叫做y轴,画成与x轴垂直.
x
y
这样,就在平面内建立了平面直角坐标系,坐标系所在的平面叫做坐标平面,公共原点O叫做直角坐标系的原点.
特别提示
(1)两条数轴要互相垂直,且有公共原点.
(2)一般情况下,两条数轴一条水平,一条铅垂.
(3)表示数轴正方向的箭头一定要画,横轴箭头旁标上x,纵轴箭头旁标上y.一般地,x轴取向右的方向为正方向,y轴取向上的方向为正方向.
(4)一般情况下,两条数轴的单位长度是统一的.
2.点的坐标
O
x
y
对于平面内任意一点M,作MM1⊥x轴,MM2⊥y轴.
设垂足M1,M2在各自数轴上所表示的数分别是x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序实数对(x,y)叫做点M的坐标.
M
M1
M2
(x,y)
建立了平面直角坐标系后,对于坐标平面内任何一点,我们可以确定它的坐标.反过来,对于任何一个坐标,我们可以在坐标平面内确定它所表示的一个点.
坐标平面内的点的坐标有什么符号特征呢?
3.点的坐标的符号特征
x轴和y轴把坐标平面分成四个象限,如图所示.
象限以数轴为界,x轴,y轴上的点不属于任何象限.
O
x
y
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
-1
-2
-3
-4
第一象限
第二象限
第三象限
第四象限
小组讨论,总结出各个象限内点的坐标的符号特征.
O
x
y
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
-1
-2
-3
-4
第一象限
第二象限
第三象限
第四象限
象限 x,y的符号
第一象限
第二象限
第三象限
第四象限
点(x,y)
四个象限中点的坐标的符号特征如下表:
(+,+)
(-,+)
(-,-)
(+,-)
(+,+)
(-,+)
(-,-)
(+,-)
例题解答
例 (1)如图,写出平面直角坐标系内点M,N,L,O,P的坐标.
解:(1)所求各点坐标为:
M(2,4),N(-2,2),
L(0,-2.5),O(0,0),P(2,-2.5).
例 (2) 在平面直角坐标系内画出点A(2,4),B(5,2), C(-3.5,0),
D(-3.5,-2).
(2)A,B,C,D各点的位置如图:
A
B
C
D
A
B
C
D
思考:点(2,4)与点(4,2)是不是同一个点?
点(-2,4)与点(2,-4)呢?
解:在图中分别找出各点进行判断.
可以看出,所给点是四个不同的点.
(2,4)
(4,2)
(-2,4)
(2,-4)
表示点的坐标的两个数是有顺序的,当a≠b时,点P(a,b)与点Q(b,a)表示不同的点.
1.下面是平面直角坐标系的为( )
随堂练习
A.
B.
C.
D.
C
2.在平面直角坐标系中,已知点P(2,-3),则点P在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:∵横坐标为正,纵坐标为负,
∴点P(2,-3)在第四象限,∴选D.
D
3.若点P(m,1-2m) 横坐标与纵坐标互为相反数,
则点P一定在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
解析:∵点P(m,1-2m)的横坐标与纵坐标互为相反数,
∴m+1-2m=0, 解得m=1, ∴点P(1,-1),
∴点P一定在第四象限.
4.根据图中各点的位置填表.
点 坐标 所在象限
或坐标轴
A
B
C
D
E
F
G
O
(4,5)
(-5,4)
(-3,-5)
(3,0)
(5,-4)
(2.5,-2.5)
(0,5.5)
(0,0)
一
二
三
x轴
四
四
y轴
x轴,y轴
课堂小结
坐标平面内点的坐标特征
位置 坐标特征 图象
第一象限
第二象限
第三象限
第四象限
x轴 正半轴
负半轴
y轴 正半轴
负半轴
原点
(+,+)
(-,+)
(-,-)
(+,-)
(+,0)
(-,0)
(0,+)
(0,-)
(0,0)
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
