浙教版数学八年级上册 2.5逆命题和逆定理 课件(共26张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 2.5逆命题和逆定理 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 800.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-13 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
第2章 特殊三角形
2.5 逆命题和逆定理
学习目标
了解逆命题、逆定理的概念.
会识别两个命题是不是互逆命题,并能写出简单命题的逆命题.
了解原命题成立,其逆命题不一定成立.
理解线段垂直平分线性质定理的逆定理.
情景导入
考虑两个命题:
“飞机是会飞的交通工具”
“会飞的交通工具是飞机”
这两个命题有什么不同?它们都是真命题吗?
温习旧识
1. 命题的概念:
一般地,判断某一件事情的句子叫做命题.
2.命题一般由_____和_____两部分组成,即它的一般形式是___________________.
3.下列句子是命题的是( )
A. 画∠AOB=45° B. 小于直角的角是锐角吗?
C. 连结CD D. 鸟是动物
条件
结论
“如果…,那么…”
D
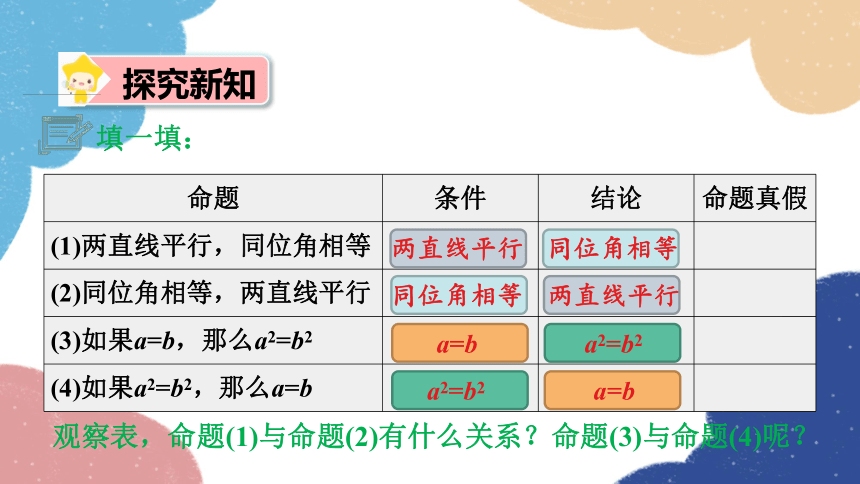
探究新知
命题 条件 结论 命题真假
(1)两直线平行,同位角相等
(2)同位角相等,两直线平行
(3)如果a=b,那么a2=b2
(4)如果a2=b2,那么a=b
观察表,命题(1)与命题(2)有什么关系?命题(3)与命题(4)呢?
填一填:
两直线平行
同位角相等
同位角相等
两直线平行
a=b
a=b
a2=b2
a2=b2
概括
互逆命题
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.
原命题与逆命题
如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题.
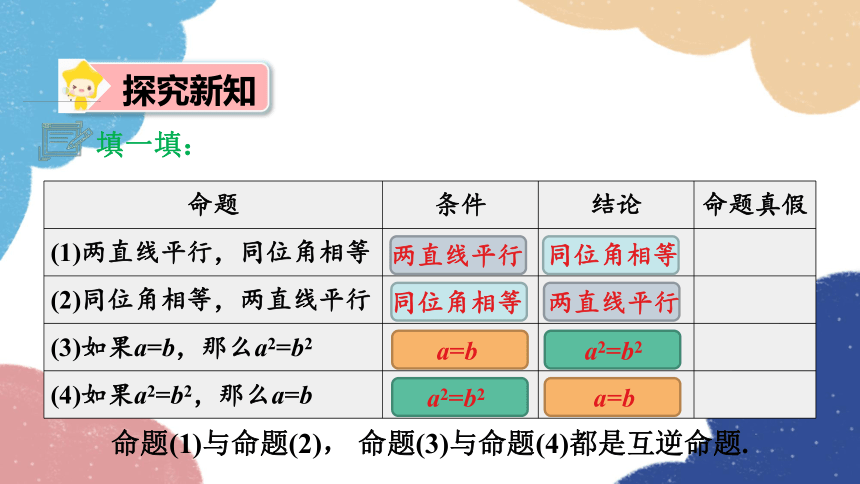
探究新知
命题 条件 结论 命题真假
(1)两直线平行,同位角相等
(2)同位角相等,两直线平行
(3)如果a=b,那么a2=b2
(4)如果a2=b2,那么a=b
命题(1)与命题(2), 命题(3)与命题(4)都是互逆命题.
填一填:
两直线平行
同位角相等
同位角相等
两直线平行
a=b
a=b
a2=b2
a2=b2
探究新知
命题 条件 结论 命题真假
(1)两直线平行,同位角相等
(2)同位角相等,两直线平行
(3)如果a=b,那么a2=b2
(4)如果a2=b2,那么a=b
填一填:
两直线平行
同位角相等
同位角相等
两直线平行
a=b
a=b
a2=b2
a2=b2
真命题
真命题
真命题
假命题
原命题是真命题,它的逆命题不一定是真命题.
做一做:
说出下列命题的逆命题,并判定命题的真假:
(1) 两直线平行,内错角相等.
(3) 磁悬浮列车是一种高速行驶时不接触地面的交通工具.
探究新知
内错角相等,两直线平行.
高速行驶时不接触地面的交通工具是磁悬浮列车.
真命题
真命题
真命题
假命题
归纳总结
每个命题都有它的逆命题,但每个真命题的逆命题不一定是真命题,同样,每个假命题的逆命题也不一定是假命题.
写出一个命题的逆命题的关键是分清它的条件和结论,然后将条件和结论互换.
探究新知
想一想:
你能根据已经学过的定理和逆命题的定义类比出逆定理的定义吗?
(一个命题经证明是真命题,就可称为定理. )
原定理和逆定理
如果一个定理的逆命题能被证明是真命题,那么就叫它是原定理的逆定理,这两个定理叫做互逆定理.
探究新知
做一做:
说出定理“线段垂直平分线上的点到这条线段两个端点的距离相等”的逆命题,并证明这个逆命题是真命题.
解:这个定理的逆命题是: 到线段两端距离相等的点在线段的垂直平分线上.下面给出证明.
已知:如图,AB是一条线段,
P是一点,且PA=PB.
求证:点P在线段AB的垂直平分线上.
A
P
B
探究新知
已知:如图,AB是一条线段,P是一点,且PA=PB.
求证:点P在线段AB的垂直平分线上.
分析:要证明点P在线段AB的垂直平分线上,可以过点P
作AB的垂线,然后证明它恰好平分线段AB.
A
P
B
已知:如图,AB是一条线段,P是一点,且PA=PB.
求证:点P在线段AB的垂直平分线上.
A
P
B
证明:(1)当点P在线段AB上,结论显然成立;
(2)当点P不在线段AB上时,作PO⊥AB于点O.
∵PA=PB,PO⊥AB,
∴OA=OB(等腰三角形三线合一).
∴PO是AB的垂直平分线.
∴点P在线段AB的垂直平分线上.
O
概括
线段垂直平分线性质定理的逆定理
①文字语言:
到线段两端距离相等的点在线段的垂直平分线上.
②几何语言:
∵PA =PB,
∴点P 在AB 的垂直平分线上.
P
A
B
C
典例精讲
例1 说出下列命题的逆命题,并判定是真命题还是假命题:
(1)同位角相等;
(2)长方形有两条对称轴.
解:
(1)的逆命题为:相等的两个角为同位角,是假命题.
(2)的逆命题为:有两条对称轴的图形为长方形,是假命题.
典例精讲
例2 下列定理中哪些有逆定理?如果有逆定理,说出它的逆定理.
(1)同旁内角互补,两直线平行;
(2)对顶角相等;
(3)三角形的两边之和大于第三边.
解: (2) (3)没有逆定理, (1) 有逆定理.
(1)的逆定理为:两直线平行,同旁内角互补.
典例精讲
例3 说出命题“两个全等三角形的面积相等”的逆命题,判断这个命题的真假,并给出证明.
解: 逆命题是 “如果两个三角形的面积相等,那么这两
个三角形全等”.
分析:说明一个命题是真命题需经过证明,而说明一个命
题是假命题只需举一个反例即可.
典例精讲
解: 逆命题是 “如果两个三角形的面积相等,那么这两
个三角形全等”.
如图,在△ABC和△ABE中,
CD、EF分别是△ABC和△ABE的AB边上的高线,
且CD=EF,
则△ABC和△ABE的面积相等,
但显然它们不全等.
所以这个逆命题是假命题.
这个命题是假命题. 举反例如下:
D
A
F
B
C
E
1. 判断下列说法是否正确?如果不正确,请说明理由.
(1) 每个定理都有逆定理;
(2) 每个命题都有逆命题;
(3) 互逆命题同真同假;
(4) 对顶角相等没有逆定理.
每个定理不一定有逆定理,
只有定理的逆命题是真命题时才称它为原定理的逆定理.
随堂练习
每个真命题的逆命题不一定
是真命题,每个假命题的逆命题也不一定是假命题.
2. 写出下列各命题的逆命题,并判断逆命题的真假:
(1) 如果|a|=|b|,那么a=b;
(2) 等边三角形的三个角都是60°;
(3) 互为相反数的两个数的和为0.
随堂练习
逆命题:如果a=b,那么|a|=|b|. 真命题
逆命题:三个角都是60°的三角形是等边三角形.
真命题
逆命题:如果两数和为0,那么这两个数互为相反数.
假命题
3. 判断下面两个定理是否有逆定理,若有,请写出它的逆定理,若没有,说明理由.
(1)在一个三角形中,等角对等边;
(2)四边形的内角和等于360°.
随堂练习
解:
(1)有逆定理,逆定理为:在一个三角形中,等边对等角.
(2)有逆定理,逆定理为:内角和等于360°的多边形是四
边形.
3. 求证:三角形三条边的垂直平分线相交于一点.
随堂练习
已知:在△ABC中,PD,PE分别是AB,AC的垂直平分线,相交于点P.
求证:点P也在BC的垂直平分线上.
P
D
E
A
C
B
P
D
E
A
C
证明:
连结PA,PB,PC.
∵ PD,PE分别是AB,AC的垂直平分线,
∴ PA=PB,PA=PC
(线段垂直平分线 上的点到线段
两端的距离相等) .
∴ PB=PC(等量代换),
∴点P在BC的垂直平分线上
(到线段两端距离相等的点在线段的垂直平分线上).
B
课堂小结
这节课我们学到了什么?
① 逆命题、逆定理的概念;
② 能写出一个命题的逆命题;
③ 在证明假命题时会用举反例说明;
④ 线段垂直平分线性质定理的逆定理.
感谢观看!
第2章 特殊三角形
2.5 逆命题和逆定理
学习目标
了解逆命题、逆定理的概念.
会识别两个命题是不是互逆命题,并能写出简单命题的逆命题.
了解原命题成立,其逆命题不一定成立.
理解线段垂直平分线性质定理的逆定理.
情景导入
考虑两个命题:
“飞机是会飞的交通工具”
“会飞的交通工具是飞机”
这两个命题有什么不同?它们都是真命题吗?
温习旧识
1. 命题的概念:
一般地,判断某一件事情的句子叫做命题.
2.命题一般由_____和_____两部分组成,即它的一般形式是___________________.
3.下列句子是命题的是( )
A. 画∠AOB=45° B. 小于直角的角是锐角吗?
C. 连结CD D. 鸟是动物
条件
结论
“如果…,那么…”
D
探究新知
命题 条件 结论 命题真假
(1)两直线平行,同位角相等
(2)同位角相等,两直线平行
(3)如果a=b,那么a2=b2
(4)如果a2=b2,那么a=b
观察表,命题(1)与命题(2)有什么关系?命题(3)与命题(4)呢?
填一填:
两直线平行
同位角相等
同位角相等
两直线平行
a=b
a=b
a2=b2
a2=b2
概括
互逆命题
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.
原命题与逆命题
如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题.
探究新知
命题 条件 结论 命题真假
(1)两直线平行,同位角相等
(2)同位角相等,两直线平行
(3)如果a=b,那么a2=b2
(4)如果a2=b2,那么a=b
命题(1)与命题(2), 命题(3)与命题(4)都是互逆命题.
填一填:
两直线平行
同位角相等
同位角相等
两直线平行
a=b
a=b
a2=b2
a2=b2
探究新知
命题 条件 结论 命题真假
(1)两直线平行,同位角相等
(2)同位角相等,两直线平行
(3)如果a=b,那么a2=b2
(4)如果a2=b2,那么a=b
填一填:
两直线平行
同位角相等
同位角相等
两直线平行
a=b
a=b
a2=b2
a2=b2
真命题
真命题
真命题
假命题
原命题是真命题,它的逆命题不一定是真命题.
做一做:
说出下列命题的逆命题,并判定命题的真假:
(1) 两直线平行,内错角相等.
(3) 磁悬浮列车是一种高速行驶时不接触地面的交通工具.
探究新知
内错角相等,两直线平行.
高速行驶时不接触地面的交通工具是磁悬浮列车.
真命题
真命题
真命题
假命题
归纳总结
每个命题都有它的逆命题,但每个真命题的逆命题不一定是真命题,同样,每个假命题的逆命题也不一定是假命题.
写出一个命题的逆命题的关键是分清它的条件和结论,然后将条件和结论互换.
探究新知
想一想:
你能根据已经学过的定理和逆命题的定义类比出逆定理的定义吗?
(一个命题经证明是真命题,就可称为定理. )
原定理和逆定理
如果一个定理的逆命题能被证明是真命题,那么就叫它是原定理的逆定理,这两个定理叫做互逆定理.
探究新知
做一做:
说出定理“线段垂直平分线上的点到这条线段两个端点的距离相等”的逆命题,并证明这个逆命题是真命题.
解:这个定理的逆命题是: 到线段两端距离相等的点在线段的垂直平分线上.下面给出证明.
已知:如图,AB是一条线段,
P是一点,且PA=PB.
求证:点P在线段AB的垂直平分线上.
A
P
B
探究新知
已知:如图,AB是一条线段,P是一点,且PA=PB.
求证:点P在线段AB的垂直平分线上.
分析:要证明点P在线段AB的垂直平分线上,可以过点P
作AB的垂线,然后证明它恰好平分线段AB.
A
P
B
已知:如图,AB是一条线段,P是一点,且PA=PB.
求证:点P在线段AB的垂直平分线上.
A
P
B
证明:(1)当点P在线段AB上,结论显然成立;
(2)当点P不在线段AB上时,作PO⊥AB于点O.
∵PA=PB,PO⊥AB,
∴OA=OB(等腰三角形三线合一).
∴PO是AB的垂直平分线.
∴点P在线段AB的垂直平分线上.
O
概括
线段垂直平分线性质定理的逆定理
①文字语言:
到线段两端距离相等的点在线段的垂直平分线上.
②几何语言:
∵PA =PB,
∴点P 在AB 的垂直平分线上.
P
A
B
C
典例精讲
例1 说出下列命题的逆命题,并判定是真命题还是假命题:
(1)同位角相等;
(2)长方形有两条对称轴.
解:
(1)的逆命题为:相等的两个角为同位角,是假命题.
(2)的逆命题为:有两条对称轴的图形为长方形,是假命题.
典例精讲
例2 下列定理中哪些有逆定理?如果有逆定理,说出它的逆定理.
(1)同旁内角互补,两直线平行;
(2)对顶角相等;
(3)三角形的两边之和大于第三边.
解: (2) (3)没有逆定理, (1) 有逆定理.
(1)的逆定理为:两直线平行,同旁内角互补.
典例精讲
例3 说出命题“两个全等三角形的面积相等”的逆命题,判断这个命题的真假,并给出证明.
解: 逆命题是 “如果两个三角形的面积相等,那么这两
个三角形全等”.
分析:说明一个命题是真命题需经过证明,而说明一个命
题是假命题只需举一个反例即可.
典例精讲
解: 逆命题是 “如果两个三角形的面积相等,那么这两
个三角形全等”.
如图,在△ABC和△ABE中,
CD、EF分别是△ABC和△ABE的AB边上的高线,
且CD=EF,
则△ABC和△ABE的面积相等,
但显然它们不全等.
所以这个逆命题是假命题.
这个命题是假命题. 举反例如下:
D
A
F
B
C
E
1. 判断下列说法是否正确?如果不正确,请说明理由.
(1) 每个定理都有逆定理;
(2) 每个命题都有逆命题;
(3) 互逆命题同真同假;
(4) 对顶角相等没有逆定理.
每个定理不一定有逆定理,
只有定理的逆命题是真命题时才称它为原定理的逆定理.
随堂练习
每个真命题的逆命题不一定
是真命题,每个假命题的逆命题也不一定是假命题.
2. 写出下列各命题的逆命题,并判断逆命题的真假:
(1) 如果|a|=|b|,那么a=b;
(2) 等边三角形的三个角都是60°;
(3) 互为相反数的两个数的和为0.
随堂练习
逆命题:如果a=b,那么|a|=|b|. 真命题
逆命题:三个角都是60°的三角形是等边三角形.
真命题
逆命题:如果两数和为0,那么这两个数互为相反数.
假命题
3. 判断下面两个定理是否有逆定理,若有,请写出它的逆定理,若没有,说明理由.
(1)在一个三角形中,等角对等边;
(2)四边形的内角和等于360°.
随堂练习
解:
(1)有逆定理,逆定理为:在一个三角形中,等边对等角.
(2)有逆定理,逆定理为:内角和等于360°的多边形是四
边形.
3. 求证:三角形三条边的垂直平分线相交于一点.
随堂练习
已知:在△ABC中,PD,PE分别是AB,AC的垂直平分线,相交于点P.
求证:点P也在BC的垂直平分线上.
P
D
E
A
C
B
P
D
E
A
C
证明:
连结PA,PB,PC.
∵ PD,PE分别是AB,AC的垂直平分线,
∴ PA=PB,PA=PC
(线段垂直平分线 上的点到线段
两端的距离相等) .
∴ PB=PC(等量代换),
∴点P在BC的垂直平分线上
(到线段两端距离相等的点在线段的垂直平分线上).
B
课堂小结
这节课我们学到了什么?
① 逆命题、逆定理的概念;
② 能写出一个命题的逆命题;
③ 在证明假命题时会用举反例说明;
④ 线段垂直平分线性质定理的逆定理.
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
