浙教版九年级数学上册第一章 二次函数 单元检测(基础篇)(含答案)
文档属性
| 名称 | 浙教版九年级数学上册第一章 二次函数 单元检测(基础篇)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 182.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 11:29:00 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
浙教版九年级数学上册第一章 二次函数 单元检测(基础篇)
一、单选题(共10题;共20分)
1.在圆的面积公式S=πr2中,s与r的关系是( )
A. 一次函数关系 B. 正比例函数关系 C. 二次函数关系 D. 不是函数关系
2.若二次函数的图象经过点P(2,8),则该图象必经过点
A. (2,-8) B. (-2,8) C. (8,-2) D. (-8,2)
3.下列各式中,y是x的二次函数的是( )
A. xy+x2=1 B. x2+y-2=0 C. y2-ax=-2 D. x2-y2+1=0
4.如图,将函数y= (x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
A. B. C. D.
5.二次函数y=x2+4x+3的图象可以由二次函数y=x2的图象平移而得到,下列平移正确的是( )
A. 先向左平移2个单位,再向上平移1个单位 B. 先向左平移2个单位,再向下平移1个单位
C. 先向右平移2个单位,再向上平移1个单位 D. 先向右平移2个单位,再向下平移1个单位
6.当ab>0时,y=ax2与y=ax+b的图象大致是( )
A. B. C. D.
7.设函数 , ,若当 时, ,则( )
A. 当 时, B. 当 时,
C. 当 时, D. 当 时,
8.在﹣3、﹣2、﹣1、0、1、2这六个数中,随机取出一个数,记为m,若数m使关于x的分式方程 ﹣1= 的解是正实数或零,且使得的二次函数y=﹣x2+(2m﹣1)x+1的图象,在x>1时,y随x的增大而减小,则满足条件的所有m之和是( )
A. ﹣2 B. ﹣1 C. 0 D. 2
9.已知抛物线y=x2-x-1与x轴的一个交点为(m,0),则代数式m2-m+2010的值为( )
A. 2008 B. 2009 C. 2010 D. 2011
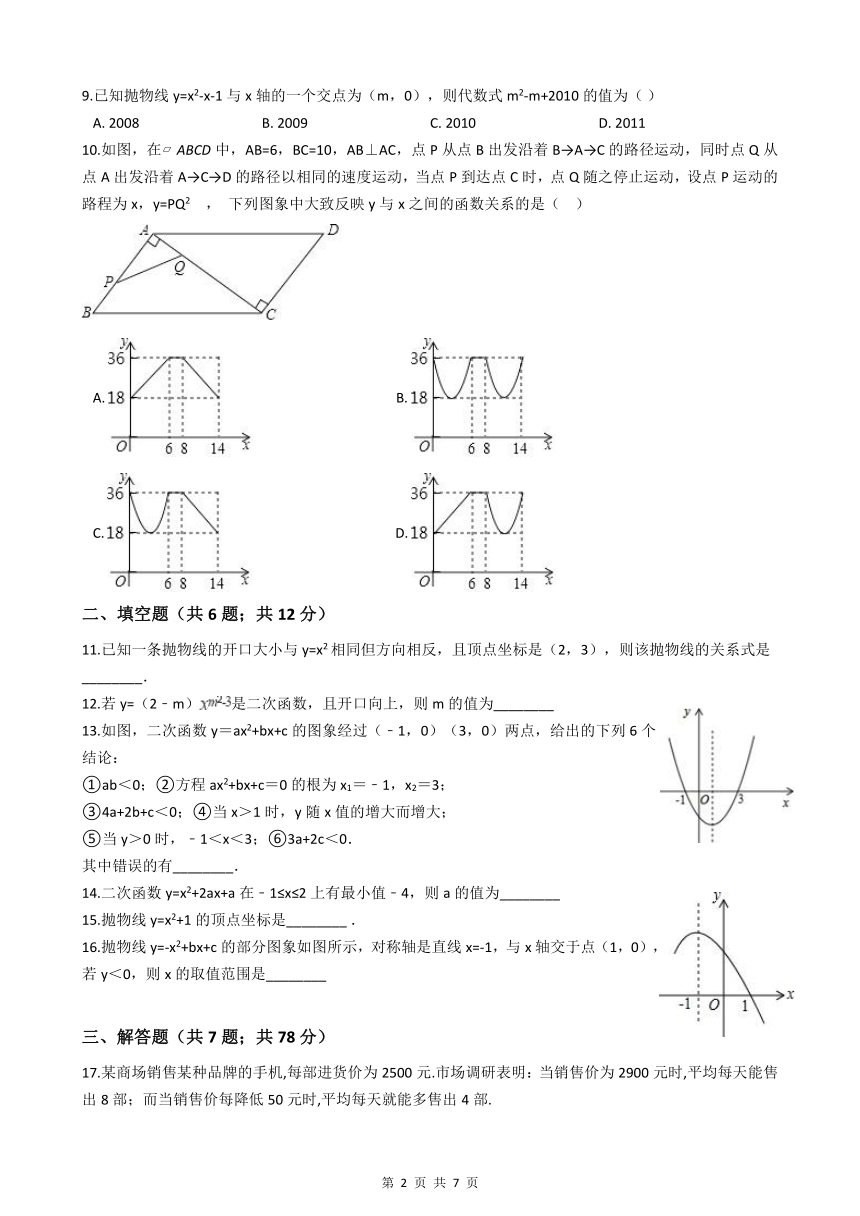
10.如图,在 ABCD中,AB=6,BC=10,AB⊥AC,点P从点B出发沿着B→A→C的路径运动,同时点Q从点A出发沿着A→C→D的路径以相同的速度运动,当点P到达点C时,点Q随之停止运动,设点P运动的路程为x,y=PQ2 , 下列图象中大致反映y与x之间的函数关系的是( )
A. B.
C. D.
二、填空题(共6题;共12分)
11.已知一条抛物线的开口大小与y=x2相同但方向相反,且顶点坐标是(2,3),则该抛物线的关系式是________.
12.若y=(2﹣m)是二次函数,且开口向上,则m的值为________
13.如图,二次函数y=ax2+bx+c的图象经过(﹣1,0)(3,0)两点,给出的下列6个结论:
①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;
③4a+2b+c<0;④当x>1时,y随x值的增大而增大;
⑤当y>0时,﹣1<x<3;⑥3a+2c<0.
其中错误的有________.
14.二次函数y=x2+2ax+a在﹣1≤x≤2上有最小值﹣4,则a的值为________
15.抛物线y=x2+1的顶点坐标是________ .
16.抛物线y=-x2+bx+c的部分图象如图所示,对称轴是直线x=-1,与x轴交于点(1,0),若y<0,则x的取值范围是________
三、解答题(共7题;共78分)
17.某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部.
(1)当售价为2800元时,这种手机平均每天的销售利润达到多少元
(2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.
(3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
18.某农业合作社投资64000元共收获80吨的农产品,目前,该农产品可以以1200元/吨售出,如果储藏起来,每星期会损失2吨,且每星期需支付各种费用1600元,且同时每星期每吨价格将上涨200元.问储藏多少星期出售这批农产品可获利122000元?
19.已知二次函数y=- .
(1)将y=- +x+ 用配方法化为y=a(x-h)2+k的形式;
(2)求该函数图象与两坐标轴交点的坐标;
(3)画出该函数的图象.
20.如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣6,0)、B(2,0)、C(0,6)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足为点E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果点P的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)过点P(﹣3,m)作x轴的垂线,垂足为点F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P ,求出P 的坐标.(直接写出结果)
21.如图,二次函数 的图象与x轴交于A、B两点,与y轴交于点C,点M为抛物线的顶点,已知C(0,3),M(1,4).
(1)求抛物线的解析式;
(2)求△MCB的面积.
22.如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
23.某商家销售某种商品,每件进价为40元.经过市场
调查,一周的销售量y件与销售单价x元/件满足一次函数的关系,部分数据如下表:( ,物价部门规定售价不
得高于80元)
销售单价x(元/件) … 55 60 65 70 75
一周的销售量y(件) … 450 400 350 300 250
(1)直接写出y与x的函数关系式:________
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并求出销售利润的最大值。
(3)该商家要使每周的销售利润不低于5000元,那么销售单价应控制在什么范围内?
答案
一、单选题
1. C 2. B 3. B 4. D 5. B 6. D 7. D 8. B 9. D 10.B
二、填空题
11.y=﹣x2+4x﹣1 12.13. ⑤ 14. 5或15. (0,1) 16. x<-3或x>1.
三、解答题
17. 解:(1)当售价为2800元时,销售价降低100元,平均每天就能售出16部.
所以:这种手机平均每天的销售利润为:16×(2800-2500)=4800(元);
(2)根据题意,得y=(2900-2500-x)(8+4×),
即y=x2+24x+3200;
(3)对于y=x2+24x+3200, 当x==150时,
y最大值=(2900-2500-150)(8+4×)=5000(元)
2900-150=2750(元)
所以,每台手机降价2750元时,商场每天销售这种手机的利润最大,最大利润是5000元.
18. 解:设储藏x星期出售这批农产品可获利122000元,
由题意得(1200+200x)×(80﹣2x)﹣1600x﹣64000=122000,
解得:x=15.
答:储藏15星期出售这批农产品可获利122000元.
19. (1)解:y=- =- (x2-2x+1-1)+ =- (x-1)2+2;
(2)解:当x=0时,y=- = ,则抛物线与y轴的交点坐标为(0, ),
当y=0时,- (x-1)2+2=0,解得x1=3,x2=-1,则抛物线与x轴的交点坐标为(3,0),(-1,0),
(3)解:如图,
20. (1)解:∵抛物线y=ax2+bx+c经过点A(﹣6,0),B(2,0),C(0,6)三点,
∴ ,解得: ,∴抛物线解析式为:y= x2﹣2x+6,
∵ , ,
∴抛物线的顶点D(﹣2,8)
(2)解:∵A(﹣6,0),D(﹣2,8),
∴设AD的解析式y=2x+12,
∵点P在AD上,∴P(x,2x+12),
∴S△APE= PE yP= ×(﹣x) (2x+12)=﹣x2﹣6x,
当x=-3时,S最大=9
(3)解:P′( , ).
点P在AD上,
∴当﹣3时,y=2×(﹣3)+12=6,∴点P(﹣3,6),∴PF=6,PE=3,
过点P′作P′M⊥y轴于点M,
∵△PEF沿EF翻折得△P′EF,
∴∠PFE=∠P′FE,PF=P′F=6,PE=P′E=3,
∵PF∥y轴,∴∠PFE=∠FEN,
∵∠PFE=∠P′FE,∴∠FEN=∠P′FE,
∴EN=FN,
设EN=a,则FN=a,P′N=6﹣a,
在Rt△P′EN中,P′N2+P′E2=EN2 , 即(6﹣a)2+32=a2 , 解得:a= ,
∵S△P′EN= P′N P′E= EN P′M,∴P′M= ,
在Rt△EMP′中,EM= ,
∴OM=EO﹣EM=6﹣ = ,
∴P′( , ).
21. (1)解:由题意可得,
把点C代入得,a=-1
∴
(2)解:令y=0,则B的坐标为 .
过点M作MD⊥y轴交于点D.
22. (1)解:由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),
∴ ,
解得: ,
∴抛物线的解析式为:y=﹣ t2+5t+ ,
∴当t= 时,y最大=4.5;
(2)解:把x=28代入x=10t得t=2.8,
∴当t=2.8时,y=﹣ ×2.82+5×2.8+ =2.25<2.44,
∴他能将球直接射入球门.
23. (1)y=-10x+1000
(2)解:S=(x-40) (-10x+1000)=- 10(x-70)2+9000
∵x=70在范围40≤x≤80之间∴当x=70时,s最大=9000
(3)解:当s=5000时,则- 10(x-70)2+9000=5000,
解之: x1=50,x2=90,
∵40≤x≤80
∴当50≤x≤80时,利润不低于5000元。
(
第
- 1 -
页 共
9
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
浙教版九年级数学上册第一章 二次函数 单元检测(基础篇)
一、单选题(共10题;共20分)
1.在圆的面积公式S=πr2中,s与r的关系是( )
A. 一次函数关系 B. 正比例函数关系 C. 二次函数关系 D. 不是函数关系
2.若二次函数的图象经过点P(2,8),则该图象必经过点
A. (2,-8) B. (-2,8) C. (8,-2) D. (-8,2)
3.下列各式中,y是x的二次函数的是( )
A. xy+x2=1 B. x2+y-2=0 C. y2-ax=-2 D. x2-y2+1=0
4.如图,将函数y= (x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
A. B. C. D.
5.二次函数y=x2+4x+3的图象可以由二次函数y=x2的图象平移而得到,下列平移正确的是( )
A. 先向左平移2个单位,再向上平移1个单位 B. 先向左平移2个单位,再向下平移1个单位
C. 先向右平移2个单位,再向上平移1个单位 D. 先向右平移2个单位,再向下平移1个单位
6.当ab>0时,y=ax2与y=ax+b的图象大致是( )
A. B. C. D.
7.设函数 , ,若当 时, ,则( )
A. 当 时, B. 当 时,
C. 当 时, D. 当 时,
8.在﹣3、﹣2、﹣1、0、1、2这六个数中,随机取出一个数,记为m,若数m使关于x的分式方程 ﹣1= 的解是正实数或零,且使得的二次函数y=﹣x2+(2m﹣1)x+1的图象,在x>1时,y随x的增大而减小,则满足条件的所有m之和是( )
A. ﹣2 B. ﹣1 C. 0 D. 2
9.已知抛物线y=x2-x-1与x轴的一个交点为(m,0),则代数式m2-m+2010的值为( )
A. 2008 B. 2009 C. 2010 D. 2011
10.如图,在 ABCD中,AB=6,BC=10,AB⊥AC,点P从点B出发沿着B→A→C的路径运动,同时点Q从点A出发沿着A→C→D的路径以相同的速度运动,当点P到达点C时,点Q随之停止运动,设点P运动的路程为x,y=PQ2 , 下列图象中大致反映y与x之间的函数关系的是( )
A. B.
C. D.
二、填空题(共6题;共12分)
11.已知一条抛物线的开口大小与y=x2相同但方向相反,且顶点坐标是(2,3),则该抛物线的关系式是________.
12.若y=(2﹣m)是二次函数,且开口向上,则m的值为________
13.如图,二次函数y=ax2+bx+c的图象经过(﹣1,0)(3,0)两点,给出的下列6个结论:
①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;
③4a+2b+c<0;④当x>1时,y随x值的增大而增大;
⑤当y>0时,﹣1<x<3;⑥3a+2c<0.
其中错误的有________.
14.二次函数y=x2+2ax+a在﹣1≤x≤2上有最小值﹣4,则a的值为________
15.抛物线y=x2+1的顶点坐标是________ .
16.抛物线y=-x2+bx+c的部分图象如图所示,对称轴是直线x=-1,与x轴交于点(1,0),若y<0,则x的取值范围是________
三、解答题(共7题;共78分)
17.某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部.
(1)当售价为2800元时,这种手机平均每天的销售利润达到多少元
(2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.
(3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
18.某农业合作社投资64000元共收获80吨的农产品,目前,该农产品可以以1200元/吨售出,如果储藏起来,每星期会损失2吨,且每星期需支付各种费用1600元,且同时每星期每吨价格将上涨200元.问储藏多少星期出售这批农产品可获利122000元?
19.已知二次函数y=- .
(1)将y=- +x+ 用配方法化为y=a(x-h)2+k的形式;
(2)求该函数图象与两坐标轴交点的坐标;
(3)画出该函数的图象.
20.如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣6,0)、B(2,0)、C(0,6)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足为点E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果点P的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)过点P(﹣3,m)作x轴的垂线,垂足为点F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P ,求出P 的坐标.(直接写出结果)
21.如图,二次函数 的图象与x轴交于A、B两点,与y轴交于点C,点M为抛物线的顶点,已知C(0,3),M(1,4).
(1)求抛物线的解析式;
(2)求△MCB的面积.
22.如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
23.某商家销售某种商品,每件进价为40元.经过市场
调查,一周的销售量y件与销售单价x元/件满足一次函数的关系,部分数据如下表:( ,物价部门规定售价不
得高于80元)
销售单价x(元/件) … 55 60 65 70 75
一周的销售量y(件) … 450 400 350 300 250
(1)直接写出y与x的函数关系式:________
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并求出销售利润的最大值。
(3)该商家要使每周的销售利润不低于5000元,那么销售单价应控制在什么范围内?
答案
一、单选题
1. C 2. B 3. B 4. D 5. B 6. D 7. D 8. B 9. D 10.B
二、填空题
11.y=﹣x2+4x﹣1 12.13. ⑤ 14. 5或15. (0,1) 16. x<-3或x>1.
三、解答题
17. 解:(1)当售价为2800元时,销售价降低100元,平均每天就能售出16部.
所以:这种手机平均每天的销售利润为:16×(2800-2500)=4800(元);
(2)根据题意,得y=(2900-2500-x)(8+4×),
即y=x2+24x+3200;
(3)对于y=x2+24x+3200, 当x==150时,
y最大值=(2900-2500-150)(8+4×)=5000(元)
2900-150=2750(元)
所以,每台手机降价2750元时,商场每天销售这种手机的利润最大,最大利润是5000元.
18. 解:设储藏x星期出售这批农产品可获利122000元,
由题意得(1200+200x)×(80﹣2x)﹣1600x﹣64000=122000,
解得:x=15.
答:储藏15星期出售这批农产品可获利122000元.
19. (1)解:y=- =- (x2-2x+1-1)+ =- (x-1)2+2;
(2)解:当x=0时,y=- = ,则抛物线与y轴的交点坐标为(0, ),
当y=0时,- (x-1)2+2=0,解得x1=3,x2=-1,则抛物线与x轴的交点坐标为(3,0),(-1,0),
(3)解:如图,
20. (1)解:∵抛物线y=ax2+bx+c经过点A(﹣6,0),B(2,0),C(0,6)三点,
∴ ,解得: ,∴抛物线解析式为:y= x2﹣2x+6,
∵ , ,
∴抛物线的顶点D(﹣2,8)
(2)解:∵A(﹣6,0),D(﹣2,8),
∴设AD的解析式y=2x+12,
∵点P在AD上,∴P(x,2x+12),
∴S△APE= PE yP= ×(﹣x) (2x+12)=﹣x2﹣6x,
当x=-3时,S最大=9
(3)解:P′( , ).
点P在AD上,
∴当﹣3时,y=2×(﹣3)+12=6,∴点P(﹣3,6),∴PF=6,PE=3,
过点P′作P′M⊥y轴于点M,
∵△PEF沿EF翻折得△P′EF,
∴∠PFE=∠P′FE,PF=P′F=6,PE=P′E=3,
∵PF∥y轴,∴∠PFE=∠FEN,
∵∠PFE=∠P′FE,∴∠FEN=∠P′FE,
∴EN=FN,
设EN=a,则FN=a,P′N=6﹣a,
在Rt△P′EN中,P′N2+P′E2=EN2 , 即(6﹣a)2+32=a2 , 解得:a= ,
∵S△P′EN= P′N P′E= EN P′M,∴P′M= ,
在Rt△EMP′中,EM= ,
∴OM=EO﹣EM=6﹣ = ,
∴P′( , ).
21. (1)解:由题意可得,
把点C代入得,a=-1
∴
(2)解:令y=0,则B的坐标为 .
过点M作MD⊥y轴交于点D.
22. (1)解:由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),
∴ ,
解得: ,
∴抛物线的解析式为:y=﹣ t2+5t+ ,
∴当t= 时,y最大=4.5;
(2)解:把x=28代入x=10t得t=2.8,
∴当t=2.8时,y=﹣ ×2.82+5×2.8+ =2.25<2.44,
∴他能将球直接射入球门.
23. (1)y=-10x+1000
(2)解:S=(x-40) (-10x+1000)=- 10(x-70)2+9000
∵x=70在范围40≤x≤80之间∴当x=70时,s最大=9000
(3)解:当s=5000时,则- 10(x-70)2+9000=5000,
解之: x1=50,x2=90,
∵40≤x≤80
∴当50≤x≤80时,利润不低于5000元。
(
第
- 1 -
页 共
9
页
)
同课章节目录
