浙教版九年级数学上册第一章 二次函数 单元检测(提高篇)(含答案)
文档属性
| 名称 | 浙教版九年级数学上册第一章 二次函数 单元检测(提高篇)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 297.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 11:29:44 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
浙教版九年级数学上册第一章 二次函数 单元检测(提高篇)
一、单选题(共10题;共20分)
1.己知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,设ΔBEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图像是:( )
A. B. C. D.
2.为了备战世界杯,中国足球队在某次集训中,一队员在距离球门12米处的挑射,正好射中了2.4米高的球门横梁.若足球运行的路线是抛物线y=ax2+bx+c(如图),则下列结论:①a<-;②-<a<0; ③a-b+c>0;④0<b<-12a.其中正确的是( )
A. ①③ B. ①④ C. ②③ D. ②④
3.如图,在正方形ABCD中,AB= ,P为对角线AC上的动点,PQ⊥AC交折线A﹣D﹣C于点Q,设AP=x,△APQ的面积为y,则y与x的函数图象正确的是( )
A. B. C. D.
4.已知函数 ,则使y=k成立的x值恰好有三个,则k的值为( )
A. 0 B. 1 C. 2 D. 3
5.一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
A. b=2a+k B. a=b+k C. a>b>0 D. a>k>0
6.已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )
A. ac>0 B. 当x>0时,y随x的增大而减小
C. 2a﹣b=0 D. 方程ax2+bx+c=0的两根是x1=﹣1,x2=3
7.如图,抛物线 与x轴交于点A、B,把抛物线在x轴及其下方的部分记作 ,将 向左平移得到 , 与x轴交于点B、D,若直线 与 、 共有3个不同的交点,则m的取值范围是( )
A. B. C. D.
8.如图在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y= x2﹣2交于A,B两点,且A点在y轴左侧,P点坐标为(0,﹣4),连接PA,PB.以下说法正确的是( )
①PO2=PA PB;②当k>0时,(PA+AO)(PB﹣BO)的值随k的增大而增大;③当k=﹣ 时,BP2=BO BA;④三角形PAB面积的最小值为 .
A. ③④ B. ①② C. ②④ D. ①④
9.如图,平面直角坐标系中,抛物线 交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )
A. B. C. D.
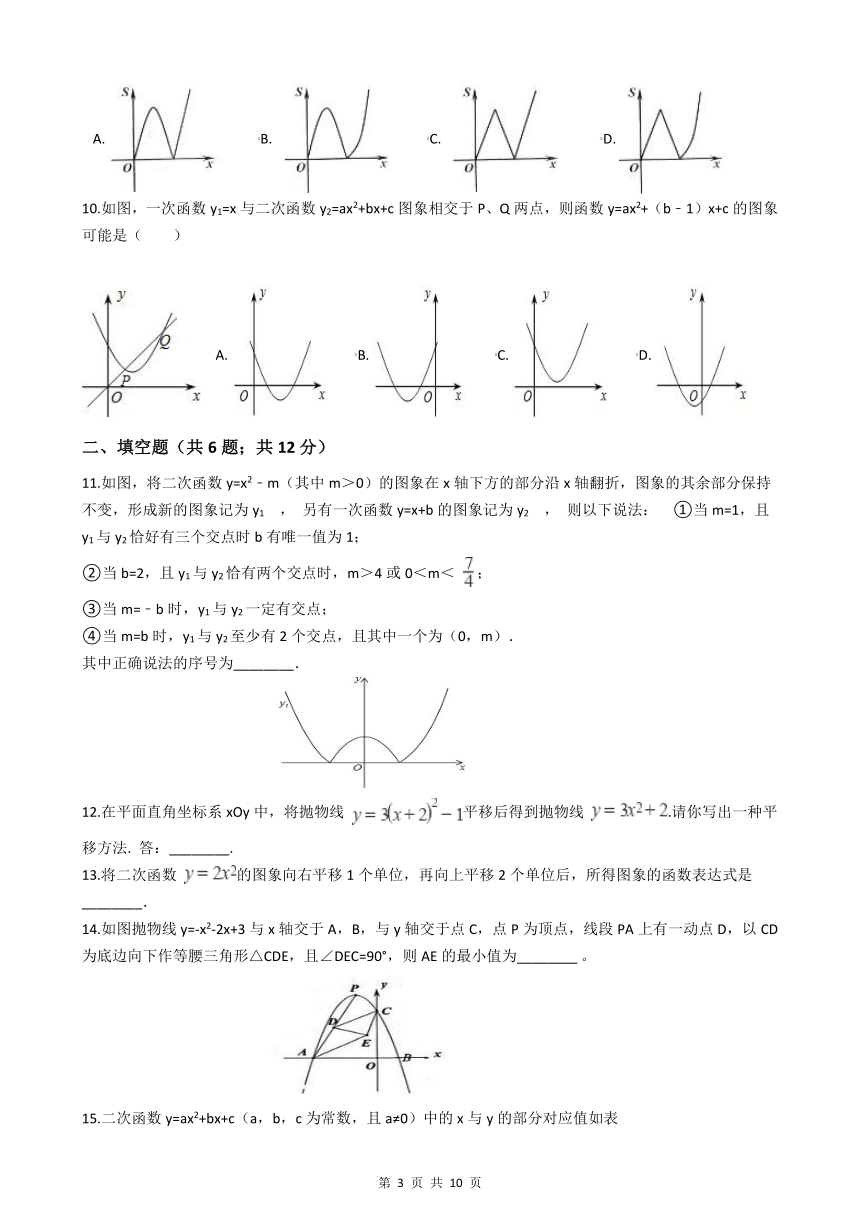
10.如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣1)x+c的图象可能是( )
A. B. C. D.
二、填空题(共6题;共12分)
11.如图,将二次函数y=x2﹣m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1 , 另有一次函数y=x+b的图象记为y2 , 则以下说法: ①当m=1,且y1与y2恰好有三个交点时b有唯一值为1;
②当b=2,且y1与y2恰有两个交点时,m>4或0<m< ;
③当m=﹣b时,y1与y2一定有交点;
④当m=b时,y1与y2至少有2个交点,且其中一个为(0,m).
其中正确说法的序号为________.
12.在平面直角坐标系xOy中,将抛物线 平移后得到抛物线 .请你写出一种平移方法. 答:________.
13.将二次函数 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是________.
14.如图抛物线y=-x2-2x+3与x轴交于A,B,与y轴交于点C,点P为顶点,线段PA上有一动点D,以CD为底边向下作等腰三角形△CDE,且∠DEC=90°,则AE的最小值为________ 。
15.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x ﹣1 0 1 3
y ﹣1 3 5 3
下列结论:
①ac<0; ②当x>1时,y的值随x值的增大而减小;
③当 时, ; ④3是方程ax2+(b﹣1)x+c=0的一个根.
其中正确的结论是________(填正确结论的序号).
16.如图,已知抛物线y=-x2-2x+3与坐标轴分别交于A,B,C三点,在抛物线上找到一点D,使得∠DCB=∠ACO,则D点坐标为________
三、综合题(共6题;共88分)
17.如图,在平面直角坐标系中,已知点A的坐标为(2,4),直线x=2与x轴交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M移动到A点时停止移动.
(1)求线段OA所在直线的函数关系式;
(2)设抛物线顶点M的横坐标为m.
① 用含m的代数式表示点P的坐标; ② 当m为何值时,线段PB最短;
(3)当线段PB最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等,若存在,求出点Q的坐标;若不存在,请说明理由.
18.如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=﹣x2+2x+3经过点A、C、A′三点.
(1)求A、A′、C三点的坐标;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积;
(3)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并写出此时M的坐标.
19.如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F: 与直线x=-2交于点P.
(1)当抛物线F经过点C时,求它的表达式;
(2)抛物线F上有两点M 、N ,若-2≤ , < ,求m的取值范围;
(3)设点P的纵坐标为 ,求 的最小值,此时抛物线F上有两点M 、N ,
若 ≤-2,比较 与 的大小;
(4)当抛物线F与线段AB有公共点时,直接写出m的取值范围。
20.如图,在平面直角坐标系中,在平面直角坐标系中,抛物线y=ax2+3x+c与x轴交于A、B两点,与y轴交于点C(0,8),直线l经过原点O,与抛物线的一个交点为D(6,8).
(1)求抛物线的解析式;
(2)抛物线的对称轴与直线l交于点E,点T为x轴上方的抛物线上的一个动点.
①当∠TEC=∠TEO时,求点T的坐标;
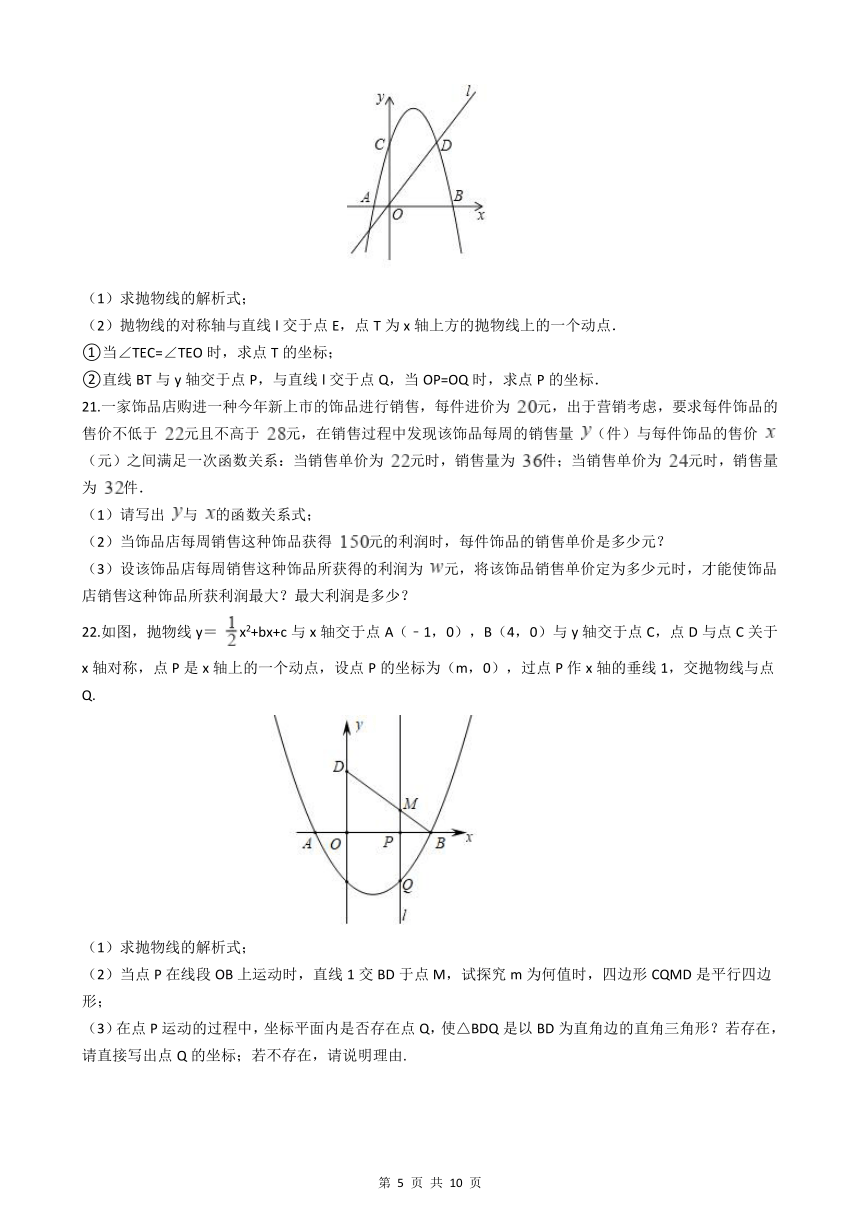
②直线BT与y轴交于点P,与直线l交于点Q,当OP=OQ时,求点P的坐标.
21.一家饰品店购进一种今年新上市的饰品进行销售,每件进价为 元,出于营销考虑,要求每件饰品的售价不低于 元且不高于 元,在销售过程中发现该饰品每周的销售量 (件)与每件饰品的售价 (元)之间满足一次函数关系:当销售单价为 元时,销售量为 件;当销售单价为 元时,销售量为 件.
(1)请写出 与 的函数关系式;
(2)当饰品店每周销售这种饰品获得 元的利润时,每件饰品的销售单价是多少元?
(3)设该饰品店每周销售这种饰品所获得的利润为 元,将该饰品销售单价定为多少元时,才能使饰品店销售这种饰品所获利润最大?最大利润是多少?
22.如图,抛物线y= x2+bx+c与x轴交于点A(﹣1,0),B(4,0)与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线1,交抛物线与点Q.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,直线1交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;
(3)在点P运动的过程中,坐标平面内是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
答 案
一、单选题
1.A 2. B 3. B 4. D 5. D 6.D 7. C 8. A 9.B 10. A
二、填空题
11.②④ 12.先向右平移2个单位长度,再向上平移3个单位
13.14. 15.①③④ 16.或(-4,-5)
三、综合题
17. (1)解:设OA所在直线的函数关系式为y=kx.
∵ A(2,4),
∴ 2k=4,∴ k=2.
∴ OA所在直线的函数关系式为y=2x
(2)解:①∵ 顶点M的横坐标为m,且在线段OA上移动,
∴y=2m (0≤m≤2).
∴ 顶点M的坐标为(m,2m).
∴ 该抛物线的函数关系式为y=(x-m)2+2m.
∴ 当x=2时,y=(2-m)2+2m=m2-2m+4 (0≤m≤2).
∴ 点P的坐标是(2,m2-2m+4).
②∵ PB= m2-2m+4=(m-1) 2+3,
又∵ 0≤m≤2,
∴ 当m=1时,PB最短.
(3)解:当线段PB最短时,点P的坐标为(2,3),
此时抛物线的函数关系式为y=(x-1)2+2. 即y=x2-2x+3.
假设在抛物线上存在点Q,使S△QMA= S△PMA.
设点Q的坐标为(x,x2-2x+3).
(Ⅰ)当点Q落在直线OA的下方时,过点P作直线PC∥AO,交y轴于点C.
∵ PB=3,AB=4,
∴ AP=1, ∴ OC=1,∴ C点的坐标为(0,-1).
∵ 点P的坐标是(2,3).
∴ 直线PC的函数关系式为y=2x-1.
∵ S△QMA= S△PMA ,
∴ 点Q落在直线y=2x-1上,
∴ x2-2x+3=2x-1, 解得,x1=x2=2,
∴ 点Q(2,3). ∴ 点Q与点P重合,
∴ 此时抛物线上不存在点Q,使△QMA与△PMA的面积相等
(Ⅱ)当点Q落在直线OA的上方时,
作点P关于点A的对称点D,过点D作直线DE∥AO,交y轴于点E.
∵ PA=1,
∴ EO=DA=1,
∴ 点E、D的坐标分别为(0,1),(2,5).
∴ 直线DE的函数关系式为y=2x+1.
∵ S△QMA= S△PMA ,
∴ 点Q落在直线y=2x+1上,
∴ x2-2x+3=2x+1.解得,x1=2+ , x2=2- .
代入y=2x+1,得y1=5+2 ,y2=5-2 .
∴ 此时抛物线上存在点
Q1(2+ ,5+2 ),Q2(2- ,5-2 ),使△QMA与△PMA的面积相等.
综上所述,抛物线上存在点Q1(2+ ,5+2 ),Q2(2- ,5-2 )
使△QMA与△PMA的面积相等
18. (1)解:当y=0时,﹣x2+2x+3=0,
解得x1=3,x2=﹣1,
则C(﹣1,0),A′(3,0),
当x=0时,y=3,则A(0,3)
(2)解:∵四边形ABOC为平行四边形,
∴AB OC , AB=OC ,
而C(﹣1,0),A(0,3),
∴B(1,3),
∴OB= = ,S△AOB= ×3×1= ,
又∵平行四边形ABOC旋转90°得平行四边形A′B′OC′,
∴∠ACO=∠OC′D , OC′=OC=1,
又∵∠ACO=∠ABO ,
∴∠ABO=∠OC′D .
又∵∠C′OD=∠AOB ,
∴△C′OD∽△BOA ,
∴ =( )2=( )2= ,
∴S△C′OD= × =
(3)解:设M点的坐标为(m , ﹣m2+2m+3),0<m<3,
作MN y轴交直线AA′于N , 易得直线AA′的解析式为y=﹣x+3,则N(m , ﹣m+3),
∵MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m ,
∴S△AMA′=S△ANM+S△MNA′
= MN 3
= (﹣m2+3m)
=﹣ m2+ m
=﹣ (m﹣ )2+ ,
∴当m= 时,S△AMA'的值最大,最大值为 ,此时M点坐标为( , ).
19. (1)解:∵抛物线F经过点C(-1,-2),∴ .∴m=-1.
∴抛物线F的表达式是
(2)解:抛物线F的对称轴为:直线x=m,当x≥m时,y随x的增大而增大;
点M、N均在直线x=-2的右侧,
∴直线x=-2必须在直线x=m右侧或与之重合
∴m≤-2
(3)解:方法一:当x=-2时, = . ∴当m=-2时, 的最小值=-2. 此时抛物线F的表达式是 .
∴当 时,y随x的增大而减小.
∵ ≤-2,∴ > . 方法二:当直线x=-2与抛物线F的对称轴(直线x=m)重合时,有最小值,此时m=-2
此时抛物线F的表达式是 .
∴当 时,y随x的增大而减小.
∵ ≤-2,∴ > .
(4)或 .
20. (1)解:把C、D两点的坐标代入抛物线解析式可得 ,解得 ,
∴抛物线解析式为y=﹣ x2+3x+8
(2)解:①∵y=﹣ x2+3x+8=﹣ (x﹣3)2+ ,
∴抛物线对称轴为x=3,
设直线l解析式为y=kx,
把D(6,8)代入可得8=6k,解得k= ,
∴直线l的解析式为y= x,
∴E(3,4),
∵O(0,0),C(0,8),∴OE=CE,
∴点E在线段OC的垂直平分线上,
∵∠TEC=∠TEO,
∴TE∥x轴,∴T的纵坐标为4,
在y=﹣ x2+3x+8中,令y=4可得4=﹣ x2+3x+8,解得x=3+ 或x=3﹣ ,
∴T的坐标为(3+ ,4)或(3﹣ ,4);
②在y=﹣ x2+3x+8中,令y=0可得0=﹣ x2+3x+8,解得x=﹣2或x=8,
∴B(8,0),
∵E(3,4),∴OE=5,
如图2,过点E作BP的平行线,交y轴于点F,交x轴于点H,
∴ = ,
∵OP=OQ,∴OF=OE=5,
∴F(0,5),
∴可设直线PB的解析式为y=kx+5,
把E点坐标代入可得4=3k+5,解得k=﹣ ,
∴直线EF的解析式为y=﹣ x+5,
∴可设直线PB的解析式为y=﹣ x+m,
把B点坐标代入可得0=﹣ ×8+m,解得m= ,
∴P点坐标为(0, )
21. (1)解:设y与x的函数关系式y=kx+b,代入题干已知数据求解:
,解得 ,
则解析式为:y=-2x+80(22≤x≤28);
(2)解:销售利润为(x-20)y=(x-20)(-2x+80)=150,
解得x=25或35(不合题意,舍去),
故每件饰品的销售单价是 元;
(3)解:由题意可得:
,…
此时当 时, 最大,但又∵ 时, 随 的增大而增大,
∴当售价不低于 元且不高于 元时,
有 , (元)
答:该饰品销售单价定为 元时,才能使饰品店销售这种饰品所获利润最大,最大利润是 元.
22. (1)解:由题意知,
∵点A(﹣1,0),B(4,0)在抛物线y= x2+bx+c上,
∴ 解得:
∴所求抛物线的解析式为
(2)解:由(1)知抛物线的解析式为 ,令x=0,得y=﹣2
∴点C的坐标为C(0,﹣2)
∵点D与点C关于x轴对称
∴点D的坐标为D(0,2)
设直线BD的解析式为:y=kx+2且B(4,0)
∴0=4k+2,解得:
∴直线BD的解析式为:
∵点P的坐标为(m,0),过点P作x轴的垂线1,交BD于点M,交抛物线与点Q
∴可设点M ,Q
∴MQ=
∵四边形CQMD是平行四边形
∴QM=CD=4,即 =4
解得:m1=2,m2=0(舍去)
∴当m=2时,四边形CQMD为平行四边形
(3)解:由题意,可设点Q 且B(4,0)、D(0,2)
∴BQ2=
DQ2= BD2=20
①当∠BDQ=90°时,则BD2+DQ2=BQ2 ,
∴
解得:m1=8,m2=﹣1,此时Q1(8,18),Q2(﹣1,0)
②当∠DBQ=90°时,则BD2+BQ2=DQ2 ,
∴
解得:m3=3,m4=4,(舍去)此时Q3(3,﹣2)
∴满足条件的点Q的坐标有三个,分别为:Q1(8,18)、Q2(﹣1,0)、Q3(3,﹣2)
(
第
- 1 -
页 共
15
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
浙教版九年级数学上册第一章 二次函数 单元检测(提高篇)
一、单选题(共10题;共20分)
1.己知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,设ΔBEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图像是:( )
A. B. C. D.
2.为了备战世界杯,中国足球队在某次集训中,一队员在距离球门12米处的挑射,正好射中了2.4米高的球门横梁.若足球运行的路线是抛物线y=ax2+bx+c(如图),则下列结论:①a<-;②-<a<0; ③a-b+c>0;④0<b<-12a.其中正确的是( )
A. ①③ B. ①④ C. ②③ D. ②④
3.如图,在正方形ABCD中,AB= ,P为对角线AC上的动点,PQ⊥AC交折线A﹣D﹣C于点Q,设AP=x,△APQ的面积为y,则y与x的函数图象正确的是( )
A. B. C. D.
4.已知函数 ,则使y=k成立的x值恰好有三个,则k的值为( )
A. 0 B. 1 C. 2 D. 3
5.一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
A. b=2a+k B. a=b+k C. a>b>0 D. a>k>0
6.已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )
A. ac>0 B. 当x>0时,y随x的增大而减小
C. 2a﹣b=0 D. 方程ax2+bx+c=0的两根是x1=﹣1,x2=3
7.如图,抛物线 与x轴交于点A、B,把抛物线在x轴及其下方的部分记作 ,将 向左平移得到 , 与x轴交于点B、D,若直线 与 、 共有3个不同的交点,则m的取值范围是( )
A. B. C. D.
8.如图在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y= x2﹣2交于A,B两点,且A点在y轴左侧,P点坐标为(0,﹣4),连接PA,PB.以下说法正确的是( )
①PO2=PA PB;②当k>0时,(PA+AO)(PB﹣BO)的值随k的增大而增大;③当k=﹣ 时,BP2=BO BA;④三角形PAB面积的最小值为 .
A. ③④ B. ①② C. ②④ D. ①④
9.如图,平面直角坐标系中,抛物线 交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )
A. B. C. D.
10.如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣1)x+c的图象可能是( )
A. B. C. D.
二、填空题(共6题;共12分)
11.如图,将二次函数y=x2﹣m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1 , 另有一次函数y=x+b的图象记为y2 , 则以下说法: ①当m=1,且y1与y2恰好有三个交点时b有唯一值为1;
②当b=2,且y1与y2恰有两个交点时,m>4或0<m< ;
③当m=﹣b时,y1与y2一定有交点;
④当m=b时,y1与y2至少有2个交点,且其中一个为(0,m).
其中正确说法的序号为________.
12.在平面直角坐标系xOy中,将抛物线 平移后得到抛物线 .请你写出一种平移方法. 答:________.
13.将二次函数 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是________.
14.如图抛物线y=-x2-2x+3与x轴交于A,B,与y轴交于点C,点P为顶点,线段PA上有一动点D,以CD为底边向下作等腰三角形△CDE,且∠DEC=90°,则AE的最小值为________ 。
15.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x ﹣1 0 1 3
y ﹣1 3 5 3
下列结论:
①ac<0; ②当x>1时,y的值随x值的增大而减小;
③当 时, ; ④3是方程ax2+(b﹣1)x+c=0的一个根.
其中正确的结论是________(填正确结论的序号).
16.如图,已知抛物线y=-x2-2x+3与坐标轴分别交于A,B,C三点,在抛物线上找到一点D,使得∠DCB=∠ACO,则D点坐标为________
三、综合题(共6题;共88分)
17.如图,在平面直角坐标系中,已知点A的坐标为(2,4),直线x=2与x轴交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M移动到A点时停止移动.
(1)求线段OA所在直线的函数关系式;
(2)设抛物线顶点M的横坐标为m.
① 用含m的代数式表示点P的坐标; ② 当m为何值时,线段PB最短;
(3)当线段PB最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等,若存在,求出点Q的坐标;若不存在,请说明理由.
18.如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=﹣x2+2x+3经过点A、C、A′三点.
(1)求A、A′、C三点的坐标;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积;
(3)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并写出此时M的坐标.
19.如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F: 与直线x=-2交于点P.
(1)当抛物线F经过点C时,求它的表达式;
(2)抛物线F上有两点M 、N ,若-2≤ , < ,求m的取值范围;
(3)设点P的纵坐标为 ,求 的最小值,此时抛物线F上有两点M 、N ,
若 ≤-2,比较 与 的大小;
(4)当抛物线F与线段AB有公共点时,直接写出m的取值范围。
20.如图,在平面直角坐标系中,在平面直角坐标系中,抛物线y=ax2+3x+c与x轴交于A、B两点,与y轴交于点C(0,8),直线l经过原点O,与抛物线的一个交点为D(6,8).
(1)求抛物线的解析式;
(2)抛物线的对称轴与直线l交于点E,点T为x轴上方的抛物线上的一个动点.
①当∠TEC=∠TEO时,求点T的坐标;
②直线BT与y轴交于点P,与直线l交于点Q,当OP=OQ时,求点P的坐标.
21.一家饰品店购进一种今年新上市的饰品进行销售,每件进价为 元,出于营销考虑,要求每件饰品的售价不低于 元且不高于 元,在销售过程中发现该饰品每周的销售量 (件)与每件饰品的售价 (元)之间满足一次函数关系:当销售单价为 元时,销售量为 件;当销售单价为 元时,销售量为 件.
(1)请写出 与 的函数关系式;
(2)当饰品店每周销售这种饰品获得 元的利润时,每件饰品的销售单价是多少元?
(3)设该饰品店每周销售这种饰品所获得的利润为 元,将该饰品销售单价定为多少元时,才能使饰品店销售这种饰品所获利润最大?最大利润是多少?
22.如图,抛物线y= x2+bx+c与x轴交于点A(﹣1,0),B(4,0)与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线1,交抛物线与点Q.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,直线1交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;
(3)在点P运动的过程中,坐标平面内是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
答 案
一、单选题
1.A 2. B 3. B 4. D 5. D 6.D 7. C 8. A 9.B 10. A
二、填空题
11.②④ 12.先向右平移2个单位长度,再向上平移3个单位
13.14. 15.①③④ 16.或(-4,-5)
三、综合题
17. (1)解:设OA所在直线的函数关系式为y=kx.
∵ A(2,4),
∴ 2k=4,∴ k=2.
∴ OA所在直线的函数关系式为y=2x
(2)解:①∵ 顶点M的横坐标为m,且在线段OA上移动,
∴y=2m (0≤m≤2).
∴ 顶点M的坐标为(m,2m).
∴ 该抛物线的函数关系式为y=(x-m)2+2m.
∴ 当x=2时,y=(2-m)2+2m=m2-2m+4 (0≤m≤2).
∴ 点P的坐标是(2,m2-2m+4).
②∵ PB= m2-2m+4=(m-1) 2+3,
又∵ 0≤m≤2,
∴ 当m=1时,PB最短.
(3)解:当线段PB最短时,点P的坐标为(2,3),
此时抛物线的函数关系式为y=(x-1)2+2. 即y=x2-2x+3.
假设在抛物线上存在点Q,使S△QMA= S△PMA.
设点Q的坐标为(x,x2-2x+3).
(Ⅰ)当点Q落在直线OA的下方时,过点P作直线PC∥AO,交y轴于点C.
∵ PB=3,AB=4,
∴ AP=1, ∴ OC=1,∴ C点的坐标为(0,-1).
∵ 点P的坐标是(2,3).
∴ 直线PC的函数关系式为y=2x-1.
∵ S△QMA= S△PMA ,
∴ 点Q落在直线y=2x-1上,
∴ x2-2x+3=2x-1, 解得,x1=x2=2,
∴ 点Q(2,3). ∴ 点Q与点P重合,
∴ 此时抛物线上不存在点Q,使△QMA与△PMA的面积相等
(Ⅱ)当点Q落在直线OA的上方时,
作点P关于点A的对称点D,过点D作直线DE∥AO,交y轴于点E.
∵ PA=1,
∴ EO=DA=1,
∴ 点E、D的坐标分别为(0,1),(2,5).
∴ 直线DE的函数关系式为y=2x+1.
∵ S△QMA= S△PMA ,
∴ 点Q落在直线y=2x+1上,
∴ x2-2x+3=2x+1.解得,x1=2+ , x2=2- .
代入y=2x+1,得y1=5+2 ,y2=5-2 .
∴ 此时抛物线上存在点
Q1(2+ ,5+2 ),Q2(2- ,5-2 ),使△QMA与△PMA的面积相等.
综上所述,抛物线上存在点Q1(2+ ,5+2 ),Q2(2- ,5-2 )
使△QMA与△PMA的面积相等
18. (1)解:当y=0时,﹣x2+2x+3=0,
解得x1=3,x2=﹣1,
则C(﹣1,0),A′(3,0),
当x=0时,y=3,则A(0,3)
(2)解:∵四边形ABOC为平行四边形,
∴AB OC , AB=OC ,
而C(﹣1,0),A(0,3),
∴B(1,3),
∴OB= = ,S△AOB= ×3×1= ,
又∵平行四边形ABOC旋转90°得平行四边形A′B′OC′,
∴∠ACO=∠OC′D , OC′=OC=1,
又∵∠ACO=∠ABO ,
∴∠ABO=∠OC′D .
又∵∠C′OD=∠AOB ,
∴△C′OD∽△BOA ,
∴ =( )2=( )2= ,
∴S△C′OD= × =
(3)解:设M点的坐标为(m , ﹣m2+2m+3),0<m<3,
作MN y轴交直线AA′于N , 易得直线AA′的解析式为y=﹣x+3,则N(m , ﹣m+3),
∵MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m ,
∴S△AMA′=S△ANM+S△MNA′
= MN 3
= (﹣m2+3m)
=﹣ m2+ m
=﹣ (m﹣ )2+ ,
∴当m= 时,S△AMA'的值最大,最大值为 ,此时M点坐标为( , ).
19. (1)解:∵抛物线F经过点C(-1,-2),∴ .∴m=-1.
∴抛物线F的表达式是
(2)解:抛物线F的对称轴为:直线x=m,当x≥m时,y随x的增大而增大;
点M、N均在直线x=-2的右侧,
∴直线x=-2必须在直线x=m右侧或与之重合
∴m≤-2
(3)解:方法一:当x=-2时, = . ∴当m=-2时, 的最小值=-2. 此时抛物线F的表达式是 .
∴当 时,y随x的增大而减小.
∵ ≤-2,∴ > . 方法二:当直线x=-2与抛物线F的对称轴(直线x=m)重合时,有最小值,此时m=-2
此时抛物线F的表达式是 .
∴当 时,y随x的增大而减小.
∵ ≤-2,∴ > .
(4)或 .
20. (1)解:把C、D两点的坐标代入抛物线解析式可得 ,解得 ,
∴抛物线解析式为y=﹣ x2+3x+8
(2)解:①∵y=﹣ x2+3x+8=﹣ (x﹣3)2+ ,
∴抛物线对称轴为x=3,
设直线l解析式为y=kx,
把D(6,8)代入可得8=6k,解得k= ,
∴直线l的解析式为y= x,
∴E(3,4),
∵O(0,0),C(0,8),∴OE=CE,
∴点E在线段OC的垂直平分线上,
∵∠TEC=∠TEO,
∴TE∥x轴,∴T的纵坐标为4,
在y=﹣ x2+3x+8中,令y=4可得4=﹣ x2+3x+8,解得x=3+ 或x=3﹣ ,
∴T的坐标为(3+ ,4)或(3﹣ ,4);
②在y=﹣ x2+3x+8中,令y=0可得0=﹣ x2+3x+8,解得x=﹣2或x=8,
∴B(8,0),
∵E(3,4),∴OE=5,
如图2,过点E作BP的平行线,交y轴于点F,交x轴于点H,
∴ = ,
∵OP=OQ,∴OF=OE=5,
∴F(0,5),
∴可设直线PB的解析式为y=kx+5,
把E点坐标代入可得4=3k+5,解得k=﹣ ,
∴直线EF的解析式为y=﹣ x+5,
∴可设直线PB的解析式为y=﹣ x+m,
把B点坐标代入可得0=﹣ ×8+m,解得m= ,
∴P点坐标为(0, )
21. (1)解:设y与x的函数关系式y=kx+b,代入题干已知数据求解:
,解得 ,
则解析式为:y=-2x+80(22≤x≤28);
(2)解:销售利润为(x-20)y=(x-20)(-2x+80)=150,
解得x=25或35(不合题意,舍去),
故每件饰品的销售单价是 元;
(3)解:由题意可得:
,…
此时当 时, 最大,但又∵ 时, 随 的增大而增大,
∴当售价不低于 元且不高于 元时,
有 , (元)
答:该饰品销售单价定为 元时,才能使饰品店销售这种饰品所获利润最大,最大利润是 元.
22. (1)解:由题意知,
∵点A(﹣1,0),B(4,0)在抛物线y= x2+bx+c上,
∴ 解得:
∴所求抛物线的解析式为
(2)解:由(1)知抛物线的解析式为 ,令x=0,得y=﹣2
∴点C的坐标为C(0,﹣2)
∵点D与点C关于x轴对称
∴点D的坐标为D(0,2)
设直线BD的解析式为:y=kx+2且B(4,0)
∴0=4k+2,解得:
∴直线BD的解析式为:
∵点P的坐标为(m,0),过点P作x轴的垂线1,交BD于点M,交抛物线与点Q
∴可设点M ,Q
∴MQ=
∵四边形CQMD是平行四边形
∴QM=CD=4,即 =4
解得:m1=2,m2=0(舍去)
∴当m=2时,四边形CQMD为平行四边形
(3)解:由题意,可设点Q 且B(4,0)、D(0,2)
∴BQ2=
DQ2= BD2=20
①当∠BDQ=90°时,则BD2+DQ2=BQ2 ,
∴
解得:m1=8,m2=﹣1,此时Q1(8,18),Q2(﹣1,0)
②当∠DBQ=90°时,则BD2+BQ2=DQ2 ,
∴
解得:m3=3,m4=4,(舍去)此时Q3(3,﹣2)
∴满足条件的点Q的坐标有三个,分别为:Q1(8,18)、Q2(﹣1,0)、Q3(3,﹣2)
(
第
- 1 -
页 共
15
页
)
同课章节目录
