有理数乘方1(浙江省杭州市富阳市)

课件21张PPT。棋盘上的麦粒
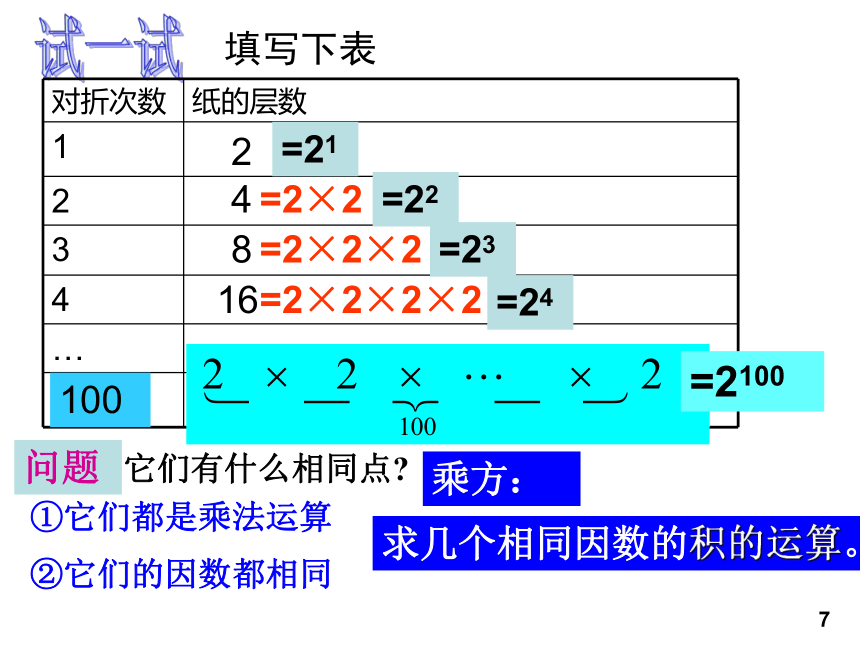
在印度有一个古老的传说：舍罕王打算奖赏国际象棋的发明人—宰相达依尔。国王问他想要什么，他对国王说：“陛下，请您在这张棋盘的第1个小格里，赏给我1粒麦子，在第2个小格里给2粒，第3小格给4粒，以后每一小格都比前一小格加一倍。请您按这样摆满棋盘上所有的64格的麦粒，都赏给您的仆人吧!”国王觉得这要求太容易满足了，就命令给他这些麦粒。当人们把一袋一袋的麦子搬来开始计数时，国王才发现：就是把全印度甚至全世界的麦粒全拿来，也满足不了那位宰相的要求。那么，宰相要求得到的麦粒到底有多少呢?2.5有理数的乘方1试一试填写下表21684101024=2×2=2×2×2=2×2×2×2=2×2×‥‥‥×2×2=22=24=23=210问题它们有什么相同点?①它们都是乘法运算②它们的因数都相同求几个相同因数的积的运算。乘方：=217100=2100记法、读法n个相同的因数a相乘记做________
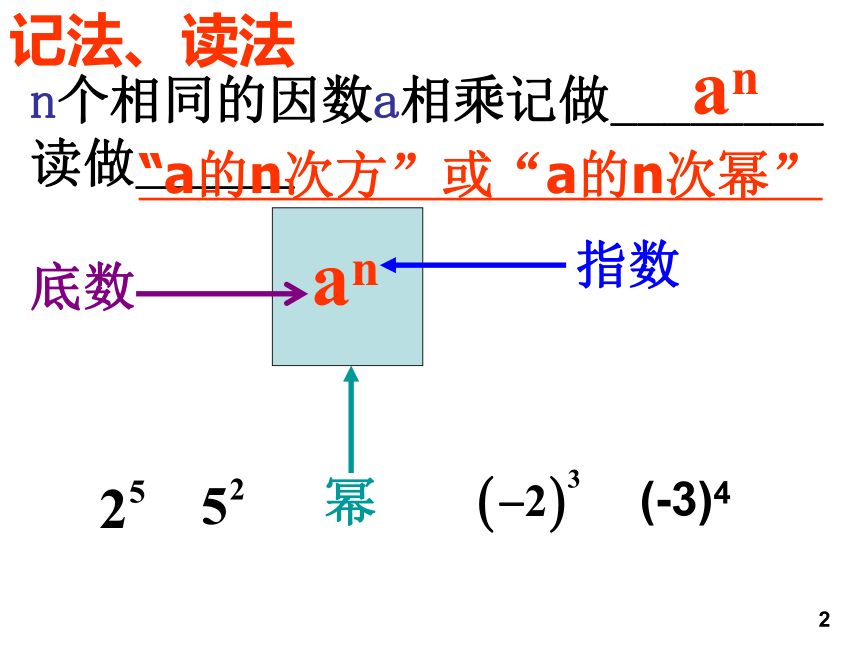
读做______ an2(-3)4 an “a的n次方”或“a的n次幂”1）在 中,12是 数,10是 数,读作
2） 的底数是 ,指数是 ,读作______________；7的7次方底指12的10次方读一读3）在 中,-3是 数,16是 数，读作__________； 4)在 中,底数是 ;指数是 ;读作_________________；底指-3的16次方17-a的17次方判一判（ ）（ ）（ ） √注意: 分数,负数的乘方,在书写时一定要把整个 分数,负数(连同符号), 用小括号括起来. 这也是辨认底数的方法指出下列各式的意义并计算结果：3你能写成乘方的形式吗？当底数为负数或分数时，要用括号括起来。你能写成乘法的形式吗？化一化-634选一选★对于(-2)4与-24，下列说法正确的是（ ）
对于(-2)3与-23，下列说法正确的是（ ）
A：它们的意义相同
B：它们的结果相同
C：它们的意义不同，结果相同
D：它们的意义不同，结果也不同 DC
2483216＋4－2－32＋16－8幂的符号规律：
1．正数的任何次幂都是正数。
2．负数的偶次幂是正数，负数的奇次幂是负数。探索＆发现3巩固＆应用1、用“＞”，“＜”，“=”比较大小(1)23____0(4)-22____0(3)-23____0(5)(-2)2____22(6) 13____ (-1)3(2)(-2)3____011-1(n为偶数)(n为奇数)分类讨论＜＜＜＞＞=(-1)2n ① 34 ② 43 ③

④ ⑤ ⑥算一算问：乘方计算要注意什么？=81=64= - 0.04= 0.043(1) (-3)2 (2)-32

算一算比一比哪个小组最棒！请注意式子所表示的意义！05(3)(5)(4)(6)3练一练计算下列各题(1): 53 (2):
(4): －32例：计算解原式==8注意运算顺序：对于乘除和乘方的混合运算，应先算乘方，再算乘除，如遇括号，先进行括号里的计算。1
① -32÷ (-3)2 ②

③
算一算4理一理3.幂的符号法则
正数的任何次幂都是正数。
负数的奇次幂是负数，负数的偶次幂是正数 。1.乘方是特殊的乘法运算，乘方的结果叫做幂。2.乘方运算的关键是要看清底数及指数的奇偶性。4.本节课的易错点：2课堂检测
1、在 中，底数是 ，指数 ，
2、 读做 ；
3、 的结果是 数（填“正”“负”）；
4、计算： = ；

5、计算： = ；46－4的7次方或－4的7次幂负－8 某种细胞每1小时由一个分裂成两个，经过2小时这种细胞由1个能分裂成多少个？问题分裂方式如下所示:……3小时？4小时？6小时？n小时？如果下午3时有该种细胞2个，那么经过分裂，到晚上7时有几个细胞？4 变一变 5的平方是 ;-5的平方是_____；平方得25的数是_____.有没有平方得-25的有理数？一个数的平方可能是0吗？你能得出什么结论？巩固＆应用2525±5平方的非负性|a|≥0绝对值的非负性3挑战自我已知|a+3|+(b-3)2=0，求a+b的值。3棋盘上的麦粒
在印度有一个古老的传说：舍罕王打算奖赏国际象棋的发明人—宰相达依尔。国王问他想要什么，他对国王说：“陛下，请您在这张棋盘的第1个小格里，赏给我1粒麦子，在第2个小格里给2粒，第3小格给4粒，以后每一小格都比前一小格加一倍。请您把这样摆满棋盘上所有的64格的麦粒，都赏给您的仆人吧!”国王觉得这要求太容易满足了，就命令给他这些麦粒。当人们把一袋一袋的麦子搬来开始计数时，国王才发现：就是把全印度甚至全世界的麦粒全拿来，也满足不了那位宰相的要求。那么，宰相要求得到的麦粒到底有多少呢?2