2.6.2 探索勾股定理

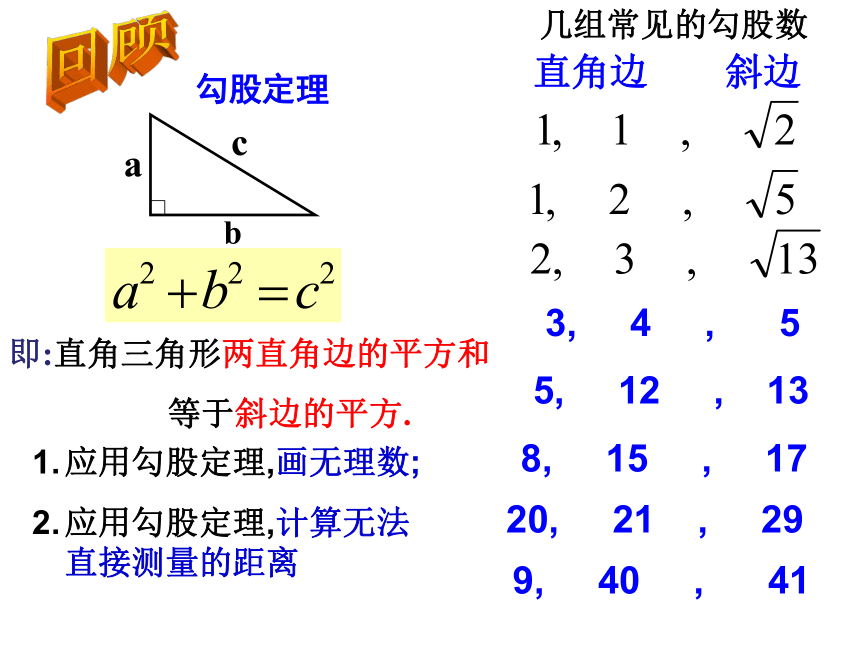
课件13张PPT。 2.6探索勾股定理（2）勾股定理即:直角三角形两直角边的平方和
等于斜边的平方.回顾几组常见的勾股数3, 4 , 5 直角边　　斜边5, 12 , 13 8, 15 , 179, 40 , 4120, 21 , 29应用勾股定理,画无理数;
应用勾股定理,计算无法直接测量的距离合作学习：(1)、画一个三角形,使其三边长分别为:（1）3cm, 4cm, 5cm；（2）5cm, 12cm,13cm；
（3）6cm, 8cm, 10cm；(2)、算一算较短两条边的平方和与最长一条边的平方是否相等?2525169169289289(3)、再用量角器量一量最大的角，判断它们是否是直角三角形？25 25169169289289由此你得到怎样的结论? 如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形. 即如果三角形的三边长a，b，c有关系 那么这个三角形是直角三角形.结论：例1 :根据下列条件，分别判断以a, b, c为边的三角形是不是直角三角形
（1）a＝7，b＝24，c＝25
解：（1）∵72+242＝252，∴以7, 24, 25为边三角形是直角三角形小结:比较较短两条边的平方和与最长一条边的平方想一想:上述哪条边所对的角是直角?1、根据下列条件，判断下面以a、b、
　c 为边的三角形是不是直角三角形?
(1)　a=5，b=7，c=8
(2)　
(3) a=3n，b=4n，c=5n (n是正整数)
(4) a: b: c=5:12:13显身手2、如图在△ABC中AB=4,BC=2,BD=1,CD=
判断下列结论是否正确，并说明理由
(1) CD ⊥AB;
解(1)∵BC2=BD2 +CD2=4(2)∵AC2=AD2+CD2=12∴∠CDB=90°∴CD⊥ABAC2+BC2=16=AB2∴∠ACB=90°∴AC⊥BC(2) AC⊥BC例2 已知△ABC三条边长分别为a, b, c,且a＝m2－n2，b＝2mn，c＝m2＋n2(m>n，m, n是正整数)。△ABC是直角三角形吗？请说明理由.解：∵ a=m2－n2，b=2mn，c＝m2＋n2∴a2+b2=(m2－n2)2+(2mn)2＝m4－2m2n2＋n4＋4m2n2＝(m2＋n2)2＝m4＋2m2n2＋n4＝c2∴△ABC是直角三角形当 m=2 n=1时,求直角三角形的三边? 如图，四边形ABCD中，AB＝3，BC=4,CD=12,AD=13, ∠B=90°，求四边形ABCD的面积.┐拓展： 三边a,b,c为边向外作正方形，正三角形，为直径
作半圆，若S1+S2=S3成立，则BABCabcS1S2S3ABCS1S2S3
如下图中分别以是直角三角形吗？ 探究：B2. 如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.1. 直角三角形的判定方法之一：归纳小结