2.4 概率的简单应用 课件(18张PPT)
文档属性
| 名称 | 2.4 概率的简单应用 课件(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 09:41:39 | ||
图片预览






文档简介
(共18张PPT)
2.4 概率的简单应用
第2章 简单事件的概率
温故知新
1.什么叫概率?
事件发生的可能性的大小叫这一事件发生的概率
2.概率的计算公式:
若事件发生的所有可能结果总数为n,事件A发生的可能结果数为m,则P(A)=
3.估计概率
在实际生活中,我们常用频率来估计概率,在大量重复的实验中发现频率接近于哪个数,把这个数作为概率.
讲授新课
1.如果有人买了彩票,一定希望知道中奖的概率有多大.那么怎么样来估计中奖的概率呢?
2.出门旅游的人希望知道乘坐哪一种交通工具发生事故的可能性较小?
概率与人们生活密切相关,在生活,生产和科研等各个领域都有着广泛的应用.
由上面三个问题,你能得到什么?
3.公司年会上的抽奖环节,你有多大的概率得到一等奖?
讲授新课
某商场举办有奖销售活动,每张奖券获奖的可能性相同,以每10000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖100个,问1张奖券中一等奖的概率是多少?中奖的概率是多少?
解:中一等奖的概率是P=
中奖的概率是P=
讲授新课
典例精析
【例1】甲乙两人玩一个游戏,判定这个游戏公平不公平的标准是( )
A.游戏的规则由甲方确定 B.游戏的规则由乙方确定
C.游戏的规则由甲乙双方确定 D.游戏双方获胜的概率相等
【详解】解:游戏的规则由甲方确定,获胜概率不一定不相等,故A不符合题意;
游戏的规则由乙方确定,获胜概率不一定不相等,故B不符合题意;
游戏的规则由甲乙双方确定,获胜概率不一定不相等,故C不符合题意;
游戏双方获胜的概率相等,故D符合题意.
故选:D.
讲授新课
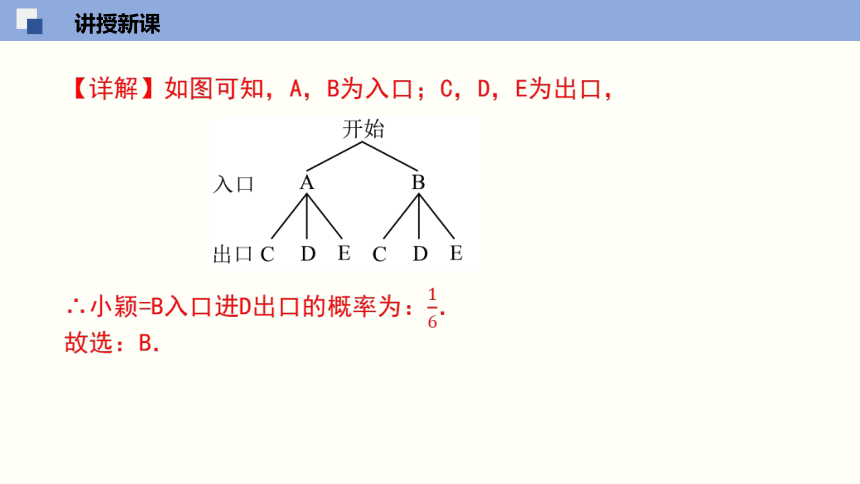
讲授新课
讲授新课
练一练
1.口袋中有10个球(每个球除颜色外都相同),其中白球x个,红球2x个,其余为蓝球.从袋中随机摸出一个球,摸到红球则甲获胜,摸到蓝球则乙获胜.要使游戏对甲、乙双方公平,则x应该等于 .
【详解】解:由题意:要想游戏公平,则双方取胜的概率应相等,
∵是放回试验,
∴红球与蓝球的个数应相等,也为2x个,
列方程可得:x+2x+2x=10,
解得x=2,
故答案为:2.
讲授新课
2.小华和小军做摸球游戏,A袋中装有编号为1,2,3的三个小球,B袋中装有编号为4,5,7的三个小球,两袋中的所有小球除编号外都相同,从两个袋子中分别随机摸出一个小球,若B袋摸出的小球的编号与A袋摸出小球的编号之差为奇数,则小华胜,否则小军胜,这个游戏对双方公平吗?请说明理由.
当堂检测
1.某口袋中有10个球,其中白球x个,绿球2x个,其余为黑球.甲从袋中任意摸出一个球,若为绿球则甲获胜,甲摸出的球放回袋中,乙从袋中摸出一个球,若为黑球则乙获胜,要使游戏对甲、乙双方公平,则x应该是( )
A.3 B.4 C.1 D.2
【详解】解:由题意甲从袋中任意摸出一个球,若为绿球则获胜;甲摸出的球放回袋中,乙从袋中摸出一个球,若为黑球则获胜可知,
绿球与黑球的个数应相等,也为2x个,
列方程可得x+2x+2x=10,
解得x=2,
故选:D.
当堂检测
2.养鱼池养了同一品种的鱼,要大概了解养鱼池中的鱼的数量,池塘的主人想出了如下的办法:“他打捞出80尾鱼,做了标记后又放回了池塘,过了三天,他又捞了一网,发现捞起的90尾鱼中,带标记的有6尾.”你认为池塘主的做法( )
A.有道理,池中大概有1200尾鱼 B.无道理
C.有道理,池中大概有7200尾鱼 D.有道理,池中大概有1280尾鱼
当堂检测
当堂检测
4.小明、小强做游戏,掷两枚均匀的硬币,若出现朝上的两个面都是正面时,小明赢,否则小强赢,该游戏对 有利.
当堂检测
5.小红和小明在操场做游戏,他们先在地上画了半径分别是2m和3m的同心圆,然后每人蒙上眼在一定距离外向圈内掷小石子,掷中阴影部分小红胜,否则小明胜,未掷入圈内不算或掷中两圆的边界线重掷,如果你是裁判,你认为游戏公平吗? .(填“公平”或“不公平”)
当堂检测
6.小兰和小青两人做游戏,有一个质量分布均匀的六面体骰子,骰子的六面分别标有1,2,3,4,5,6,如果掷出的骰子的点数是偶数,则小兰赢;如果掷出的骰子的点数是3的倍数,则小青赢,那么游戏规则对 有利.
当堂检测
7.小明和小凡一起做游戏,在一个装有2个红球和3个白球(每个球除颜色外都相同)的袋子中任意摸出一个球,规定:摸到红球小明胜,摸到白球小凡胜.
(1)你认为这个游戏对双方公平吗?请说明理由.
(2)你若认为不公平,则请你修改游戏规则,使游戏对双方公平.
当堂检测
谢 谢~
2.4 概率的简单应用
第2章 简单事件的概率
温故知新
1.什么叫概率?
事件发生的可能性的大小叫这一事件发生的概率
2.概率的计算公式:
若事件发生的所有可能结果总数为n,事件A发生的可能结果数为m,则P(A)=
3.估计概率
在实际生活中,我们常用频率来估计概率,在大量重复的实验中发现频率接近于哪个数,把这个数作为概率.
讲授新课
1.如果有人买了彩票,一定希望知道中奖的概率有多大.那么怎么样来估计中奖的概率呢?
2.出门旅游的人希望知道乘坐哪一种交通工具发生事故的可能性较小?
概率与人们生活密切相关,在生活,生产和科研等各个领域都有着广泛的应用.
由上面三个问题,你能得到什么?
3.公司年会上的抽奖环节,你有多大的概率得到一等奖?
讲授新课
某商场举办有奖销售活动,每张奖券获奖的可能性相同,以每10000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖100个,问1张奖券中一等奖的概率是多少?中奖的概率是多少?
解:中一等奖的概率是P=
中奖的概率是P=
讲授新课
典例精析
【例1】甲乙两人玩一个游戏,判定这个游戏公平不公平的标准是( )
A.游戏的规则由甲方确定 B.游戏的规则由乙方确定
C.游戏的规则由甲乙双方确定 D.游戏双方获胜的概率相等
【详解】解:游戏的规则由甲方确定,获胜概率不一定不相等,故A不符合题意;
游戏的规则由乙方确定,获胜概率不一定不相等,故B不符合题意;
游戏的规则由甲乙双方确定,获胜概率不一定不相等,故C不符合题意;
游戏双方获胜的概率相等,故D符合题意.
故选:D.
讲授新课
讲授新课
讲授新课
练一练
1.口袋中有10个球(每个球除颜色外都相同),其中白球x个,红球2x个,其余为蓝球.从袋中随机摸出一个球,摸到红球则甲获胜,摸到蓝球则乙获胜.要使游戏对甲、乙双方公平,则x应该等于 .
【详解】解:由题意:要想游戏公平,则双方取胜的概率应相等,
∵是放回试验,
∴红球与蓝球的个数应相等,也为2x个,
列方程可得:x+2x+2x=10,
解得x=2,
故答案为:2.
讲授新课
2.小华和小军做摸球游戏,A袋中装有编号为1,2,3的三个小球,B袋中装有编号为4,5,7的三个小球,两袋中的所有小球除编号外都相同,从两个袋子中分别随机摸出一个小球,若B袋摸出的小球的编号与A袋摸出小球的编号之差为奇数,则小华胜,否则小军胜,这个游戏对双方公平吗?请说明理由.
当堂检测
1.某口袋中有10个球,其中白球x个,绿球2x个,其余为黑球.甲从袋中任意摸出一个球,若为绿球则甲获胜,甲摸出的球放回袋中,乙从袋中摸出一个球,若为黑球则乙获胜,要使游戏对甲、乙双方公平,则x应该是( )
A.3 B.4 C.1 D.2
【详解】解:由题意甲从袋中任意摸出一个球,若为绿球则获胜;甲摸出的球放回袋中,乙从袋中摸出一个球,若为黑球则获胜可知,
绿球与黑球的个数应相等,也为2x个,
列方程可得x+2x+2x=10,
解得x=2,
故选:D.
当堂检测
2.养鱼池养了同一品种的鱼,要大概了解养鱼池中的鱼的数量,池塘的主人想出了如下的办法:“他打捞出80尾鱼,做了标记后又放回了池塘,过了三天,他又捞了一网,发现捞起的90尾鱼中,带标记的有6尾.”你认为池塘主的做法( )
A.有道理,池中大概有1200尾鱼 B.无道理
C.有道理,池中大概有7200尾鱼 D.有道理,池中大概有1280尾鱼
当堂检测
当堂检测
4.小明、小强做游戏,掷两枚均匀的硬币,若出现朝上的两个面都是正面时,小明赢,否则小强赢,该游戏对 有利.
当堂检测
5.小红和小明在操场做游戏,他们先在地上画了半径分别是2m和3m的同心圆,然后每人蒙上眼在一定距离外向圈内掷小石子,掷中阴影部分小红胜,否则小明胜,未掷入圈内不算或掷中两圆的边界线重掷,如果你是裁判,你认为游戏公平吗? .(填“公平”或“不公平”)
当堂检测
6.小兰和小青两人做游戏,有一个质量分布均匀的六面体骰子,骰子的六面分别标有1,2,3,4,5,6,如果掷出的骰子的点数是偶数,则小兰赢;如果掷出的骰子的点数是3的倍数,则小青赢,那么游戏规则对 有利.
当堂检测
7.小明和小凡一起做游戏,在一个装有2个红球和3个白球(每个球除颜色外都相同)的袋子中任意摸出一个球,规定:摸到红球小明胜,摸到白球小凡胜.
(1)你认为这个游戏对双方公平吗?请说明理由.
(2)你若认为不公平,则请你修改游戏规则,使游戏对双方公平.
当堂检测
谢 谢~
同课章节目录
