第2章 简单事件的概率 单元复习课件(36张PPT)
文档属性
| 名称 | 第2章 简单事件的概率 单元复习课件(36张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 09:46:03 | ||
图片预览











文档简介
(共36张PPT)
单元小结
第2章 简单事件的概率
单元小结
事件
确定事件
随机事件
必然事件
不可能事件
1.在一定条件下必然发生的事件,叫做必然事件;
2.在一定条件下不可能发生的事件,叫做不可能事件;
3.在一定条件下可能发生也可能不发生的事件,叫做随机事件.
单元小结
概率: 一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记作P(A).
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能事件
必然事件
概率的值
单元小结
1.①当实验的所有结果不是有限个,或各种可能结果发生的可能性不相等时,我们用大量重复试验中随机事件发生的稳定频率来估计概率.
②频率与概率的关系:两者都能定量地反映随机事件可能性的大小,但频率具有随机性,概率是自身固有的性质,不具有随机性.
单元小结
2.概率的计算公式:
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,那么出现每一种结果的概率都是 .
如果事件A包括其中的m种可能的结果,那么事件A发生的概率
P(A)= + +…+
n
1
n
1
n
1
m个
=
n
m
单元小结
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.
列表法中表格构造特点:
三、列表法
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
说明:如果第一个因素包含2种情况;第二个因素包含3种情况;那么所有情况n=2×3=6.
单元小结
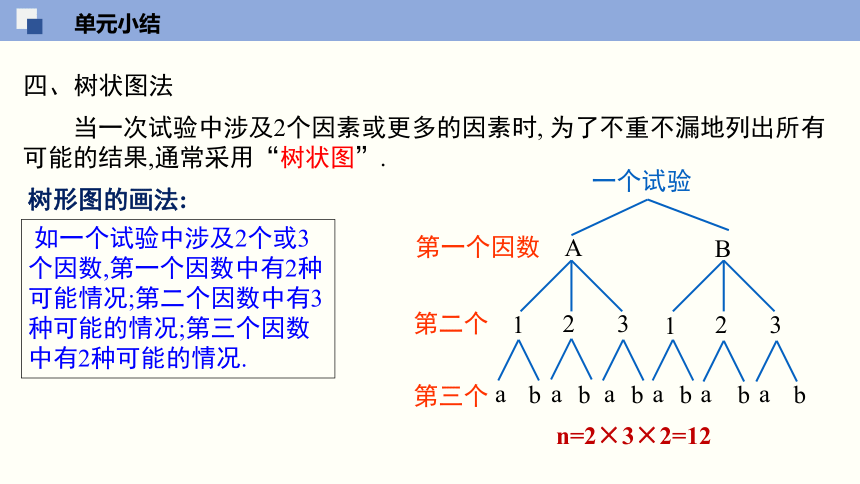
当一次试验中涉及2个因素或更多的因素时, 为了不重不漏地列出所有可能的结果,通常采用“树状图”.
树形图的画法:
一个试验
第一个因数
第二个
第三个
如一个试验中涉及2个或3个因数,第一个因数中有2种可能情况;第二个因数中有3种可能的情况;第三个因数中有2种可能的情况.
A
B
1
2
3
1
2
3
a
b
a
b
a
b
a
b
a
b
a
b
n=2×3×2=12
四、树状图法
单元小结
考点训练一 事件发生的可能性
【例1】下列事件是必然事件的是( )
A.掷一枚质地均匀的骰子,掷出的点数是偶数
B.两条线段可以组成一个三角形
C.400人中至少有两个人的生日在同一天
D.车辆随机到达一个路口,遇到绿灯
【详解】解:A. 掷一枚质地均匀的骰子,掷出的点数是偶数,是随机事件,不合题意;
B. 两条线段可以组成一个三角形,是不可能事件,不合题意;
C. 400人中至少有两个人的生日在同一天,是必然事件,符合题意;
D. 车辆随机到达一个路口,遇到绿灯,是随机事件,不合题意.
故选:C.
单元小结
针对训练
1.从一副扑克牌中任意抽取1张,则下列事件:(1)这张牌是“红色的”;(2)这张牌是“红心”的;(3)这张牌是“大王”;(4)这张牌是“A”;发生可能性最大的是(只填写序号) .
单元小结
2.书箱里只有10本大小相同、厚薄差不多的书,从中随意摸出一本,如果“摸出一本小说”是下列事件,分别确定书箱里小说的数量是多少或在什么范围内:
(1)必然事件;
(2)不可能事件;
(3)随机事件.
【详解】(1)解:如果“摸出一本小说”是必然事件,那么小说的数量是10本.
(2)解:如果“摸出一本小说”是不可能事件,那么小说的数量是0本.
(3)解:如果“摸出一本小说”是随机事件,那么0本<小说的数量<10本.
单元小结
考点训练二 概率的意义理解
【例2】若事件 表示“买一张彩票,中了特等奖”,则下列说法中,不正确的是( )
A.0<P(A)<1
B. P(A)接近0
C.对于不同类型的彩票, P(A)的值可能不一样
D.若小明买了20张彩票后中了特等奖,则可计算得P(A)=5%
单元小结
【详解】解:根据概率的意义,若事件A表示“买一张彩票,中了特等奖”,
A. 0<P(A)<1,故该选项正确,不符合题意;
B. P(A)接近0,故该选项正确,不符合题意;
C. 对于不同类型的彩票, P(A)的值可能不一样,故该选项正确,不符合题意;
D. 根据实际情况P(A)接近0,若小明买了20张彩票后中了特等奖,不能得出得P(A)=5% ,故该选项不正确,符合题意;
故选:D.
单元小结
针对训练
1.一般地,如果一个试验有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为: .必然事件发生的概率为 ,不可能事件发生的概率为 ,随机事件A发生的概率是 .
单元小结
2.一则广告声称本次活动的中奖率为20% ,其中一等奖的中奖率为1%.小明看到这则广告后,想:“我抽5张就会有1张中奖,抽100张就会有1张中一等奖.”你认为小明的想法对吗?
【详解】解:抽5张有可能都不中奖,也有可能都中奖,还有可能中一张或几张,事先不能确定.
一等奖中奖率为1%,是指在总数为100张奖券的情况下100张会有1张中一等奖,但是当总数不确定时,100张奖券中,有可能会有1张或几张中一等奖,也有可能不会中一等奖,事先不能确定.
所以小明的想法不对.
单元小结
考点训练三 根据概率公式计算概率
单元小结
针对训练
1.从1——10这10个整数中随机抽取1个数,抽到3的倍数的概率是 .
单元小结
2.任意掷一枚质地均匀的骰子.
(1)掷出的点数是4的概率是______;
(2)掷出的点数是7的概率是______;
(3)掷出的点数是偶数的概率是多少?
单元小结
考点训练四 列举法计算概率
单元小结
针对训练
1.有红、橙、黄、绿4种颜色的小球和四种对应颜色的盒子各一个,现从4个小球中任取两种颜色的小球随机放入其中的两个盒子,小球的颜色和盒子的颜色一致的概率是 .
单元小结
2.甲、乙两个口袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片所标有的三个数值分别为-2,4,-6,乙袋中的三张卡片所标的数值为-2,3,5.
(1)小明在乙袋中随机抽取一张卡片,他抽出来的卡片上所标的数值是奇数的概率是 .
(2)小红先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出的卡片上的数值,把x,y分别作为点A的横坐标和纵坐标.请用列举法写出点A(x,y)的所有情况,并求点A在第二象限的概率.
单元小结
单元小结
考点训练五 用列表法或树状图法计算概率
单元小结
单元小结
针对训练
1.某校开展“课后延时服务”后,组建了四个艺术社团:书法、合唱、剪纸、舞蹈,学校规定每人只能选择参加一个社团,小宇和小智准备随机选择一个社团报名,则小宇和小智两人刚好选择同一个社团的概率为 .
单元小结
2.小王、小李和小林三人准备打乒乓球,他们约定用“抛硬币”的方式来确定哪两个人先上场,三人手中各持有一枚质地均匀的硬币,同时将手中硬币抛落到水平地面为一个回合.落地后,三枚硬币中,恰有两枚正面向上或反面向上的这两枚硬币持有人先上场;若三枚硬币均为正面向上或反面向上,属于不确定.
(1)请你用画树状图的方式表示“抛硬币”一个回合中所有可能出现的结果;
(2)求一个回合能确定两人先上场的概率.
单元小结
单元小结
考点训练六 利用频率估计概率
【例6】在一个不透明的盒子中装有红球和白球共30个,这些球除颜色外无其它差别,随机从盒子中摸出一个球,记下球的颜色后,放回并摇匀.通过大量的实验后发现摸出白球的频率稳定在0.4,则盒子中白球的个数可能是( )
A.4 B.8 C.12 D.16
【详解】解:由题意可得:
盒子中白球的个数可能是:0.4×30=12,
故选:C.
单元小结
针对训练
1.在一个不透明的盒子中装有5枚黑棋子和若干枚白棋子,它们除颜色外完全相同,小明将盒子里的棋子摇匀,随机摸出一枚棋子,记下它的颜色后再放回盒子里.不断重复这一过程,统计发现,摸到白色棋子的频率稳定在80%,则盒子中白色棋子的数量可能是 .
单元小结
2.在一个不透明的口袋里装有红、白两种颜色的球共5只,它们除颜色外其余都相同.某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近______;(精确到0.1)
(2)试估算口袋中白球有多少只?
(3)从中先摸出一球,不放回,再摸出一球;请利用树状图或列表计算这两只球颜色不同的概率是多少?
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
单元小结
【详解】(1)当n很大时,摸到白球的频率将会接近0.6;
(2)由(1)摸到白球的概率为0.6,
所以可估计口袋中白种颜色的球的个数=5×0.6=3(只);
单元小结
考点训练七 简单概率的应用问题
单元小结
针对训练
1.如图所示,准备了三张大小相同的纸片,其中两张纸片上各画一个半径相等的半圆,另一张纸片上画一个正方形.将这三张纸片放在一个盒子里摇匀,随机地抽取两张纸片,若可以拼成一个圆形(取出的两张纸片都画有半圆形)则甲方赢;若可以拼成一个蘑菇形(取出的一张纸片画有半圆、一张画有正方形)则乙方赢.你认为这个游戏对双方是公平的吗?若不是,有利于谁? .
单元小结
【详解】解:根据游戏规则可知:从三张大小相同的纸片中随机地抽取两张纸片,共3种情况;
可以拼成一个圆形的有1种;可以拼成一个蘑茹形有2种;
故乙取胜的概率大于甲取胜的概率;
故这个游戏不公平,且对乙有利.
故答案为:不公平,乙有利.
单元小结
2.某校举行“传颂中华家风,弘扬中华美德”演讲比赛.每班选拔一人参加.七年级(1)班的小丽和小华表现都很优秀,现在打算从2位同学中任选1人参加学校演讲比赛.为此设计了如下游戏规则:在一个不透明的袋子里装有10个除号码外其余都相同的小球,小球的号码分别是1,2,3,4,5,6,7,8,9,10.将它们充分摇匀,并从中任意摸出一个小球.规定摸出小球的号码能被3整除时,则小丽去;摸出小球的号码能被5整除时,则小华去.这个游戏对双方公平吗?请说明理由.如果不公平,应该如何修改游戏规则才能对双方公平?(游戏对双方公平的原则是双方获胜的概率相等).
单元小结
谢 谢~
单元小结
第2章 简单事件的概率
单元小结
事件
确定事件
随机事件
必然事件
不可能事件
1.在一定条件下必然发生的事件,叫做必然事件;
2.在一定条件下不可能发生的事件,叫做不可能事件;
3.在一定条件下可能发生也可能不发生的事件,叫做随机事件.
单元小结
概率: 一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记作P(A).
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能事件
必然事件
概率的值
单元小结
1.①当实验的所有结果不是有限个,或各种可能结果发生的可能性不相等时,我们用大量重复试验中随机事件发生的稳定频率来估计概率.
②频率与概率的关系:两者都能定量地反映随机事件可能性的大小,但频率具有随机性,概率是自身固有的性质,不具有随机性.
单元小结
2.概率的计算公式:
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,那么出现每一种结果的概率都是 .
如果事件A包括其中的m种可能的结果,那么事件A发生的概率
P(A)= + +…+
n
1
n
1
n
1
m个
=
n
m
单元小结
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.
列表法中表格构造特点:
三、列表法
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
说明:如果第一个因素包含2种情况;第二个因素包含3种情况;那么所有情况n=2×3=6.
单元小结
当一次试验中涉及2个因素或更多的因素时, 为了不重不漏地列出所有可能的结果,通常采用“树状图”.
树形图的画法:
一个试验
第一个因数
第二个
第三个
如一个试验中涉及2个或3个因数,第一个因数中有2种可能情况;第二个因数中有3种可能的情况;第三个因数中有2种可能的情况.
A
B
1
2
3
1
2
3
a
b
a
b
a
b
a
b
a
b
a
b
n=2×3×2=12
四、树状图法
单元小结
考点训练一 事件发生的可能性
【例1】下列事件是必然事件的是( )
A.掷一枚质地均匀的骰子,掷出的点数是偶数
B.两条线段可以组成一个三角形
C.400人中至少有两个人的生日在同一天
D.车辆随机到达一个路口,遇到绿灯
【详解】解:A. 掷一枚质地均匀的骰子,掷出的点数是偶数,是随机事件,不合题意;
B. 两条线段可以组成一个三角形,是不可能事件,不合题意;
C. 400人中至少有两个人的生日在同一天,是必然事件,符合题意;
D. 车辆随机到达一个路口,遇到绿灯,是随机事件,不合题意.
故选:C.
单元小结
针对训练
1.从一副扑克牌中任意抽取1张,则下列事件:(1)这张牌是“红色的”;(2)这张牌是“红心”的;(3)这张牌是“大王”;(4)这张牌是“A”;发生可能性最大的是(只填写序号) .
单元小结
2.书箱里只有10本大小相同、厚薄差不多的书,从中随意摸出一本,如果“摸出一本小说”是下列事件,分别确定书箱里小说的数量是多少或在什么范围内:
(1)必然事件;
(2)不可能事件;
(3)随机事件.
【详解】(1)解:如果“摸出一本小说”是必然事件,那么小说的数量是10本.
(2)解:如果“摸出一本小说”是不可能事件,那么小说的数量是0本.
(3)解:如果“摸出一本小说”是随机事件,那么0本<小说的数量<10本.
单元小结
考点训练二 概率的意义理解
【例2】若事件 表示“买一张彩票,中了特等奖”,则下列说法中,不正确的是( )
A.0<P(A)<1
B. P(A)接近0
C.对于不同类型的彩票, P(A)的值可能不一样
D.若小明买了20张彩票后中了特等奖,则可计算得P(A)=5%
单元小结
【详解】解:根据概率的意义,若事件A表示“买一张彩票,中了特等奖”,
A. 0<P(A)<1,故该选项正确,不符合题意;
B. P(A)接近0,故该选项正确,不符合题意;
C. 对于不同类型的彩票, P(A)的值可能不一样,故该选项正确,不符合题意;
D. 根据实际情况P(A)接近0,若小明买了20张彩票后中了特等奖,不能得出得P(A)=5% ,故该选项不正确,符合题意;
故选:D.
单元小结
针对训练
1.一般地,如果一个试验有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为: .必然事件发生的概率为 ,不可能事件发生的概率为 ,随机事件A发生的概率是 .
单元小结
2.一则广告声称本次活动的中奖率为20% ,其中一等奖的中奖率为1%.小明看到这则广告后,想:“我抽5张就会有1张中奖,抽100张就会有1张中一等奖.”你认为小明的想法对吗?
【详解】解:抽5张有可能都不中奖,也有可能都中奖,还有可能中一张或几张,事先不能确定.
一等奖中奖率为1%,是指在总数为100张奖券的情况下100张会有1张中一等奖,但是当总数不确定时,100张奖券中,有可能会有1张或几张中一等奖,也有可能不会中一等奖,事先不能确定.
所以小明的想法不对.
单元小结
考点训练三 根据概率公式计算概率
单元小结
针对训练
1.从1——10这10个整数中随机抽取1个数,抽到3的倍数的概率是 .
单元小结
2.任意掷一枚质地均匀的骰子.
(1)掷出的点数是4的概率是______;
(2)掷出的点数是7的概率是______;
(3)掷出的点数是偶数的概率是多少?
单元小结
考点训练四 列举法计算概率
单元小结
针对训练
1.有红、橙、黄、绿4种颜色的小球和四种对应颜色的盒子各一个,现从4个小球中任取两种颜色的小球随机放入其中的两个盒子,小球的颜色和盒子的颜色一致的概率是 .
单元小结
2.甲、乙两个口袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片所标有的三个数值分别为-2,4,-6,乙袋中的三张卡片所标的数值为-2,3,5.
(1)小明在乙袋中随机抽取一张卡片,他抽出来的卡片上所标的数值是奇数的概率是 .
(2)小红先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出的卡片上的数值,把x,y分别作为点A的横坐标和纵坐标.请用列举法写出点A(x,y)的所有情况,并求点A在第二象限的概率.
单元小结
单元小结
考点训练五 用列表法或树状图法计算概率
单元小结
单元小结
针对训练
1.某校开展“课后延时服务”后,组建了四个艺术社团:书法、合唱、剪纸、舞蹈,学校规定每人只能选择参加一个社团,小宇和小智准备随机选择一个社团报名,则小宇和小智两人刚好选择同一个社团的概率为 .
单元小结
2.小王、小李和小林三人准备打乒乓球,他们约定用“抛硬币”的方式来确定哪两个人先上场,三人手中各持有一枚质地均匀的硬币,同时将手中硬币抛落到水平地面为一个回合.落地后,三枚硬币中,恰有两枚正面向上或反面向上的这两枚硬币持有人先上场;若三枚硬币均为正面向上或反面向上,属于不确定.
(1)请你用画树状图的方式表示“抛硬币”一个回合中所有可能出现的结果;
(2)求一个回合能确定两人先上场的概率.
单元小结
单元小结
考点训练六 利用频率估计概率
【例6】在一个不透明的盒子中装有红球和白球共30个,这些球除颜色外无其它差别,随机从盒子中摸出一个球,记下球的颜色后,放回并摇匀.通过大量的实验后发现摸出白球的频率稳定在0.4,则盒子中白球的个数可能是( )
A.4 B.8 C.12 D.16
【详解】解:由题意可得:
盒子中白球的个数可能是:0.4×30=12,
故选:C.
单元小结
针对训练
1.在一个不透明的盒子中装有5枚黑棋子和若干枚白棋子,它们除颜色外完全相同,小明将盒子里的棋子摇匀,随机摸出一枚棋子,记下它的颜色后再放回盒子里.不断重复这一过程,统计发现,摸到白色棋子的频率稳定在80%,则盒子中白色棋子的数量可能是 .
单元小结
2.在一个不透明的口袋里装有红、白两种颜色的球共5只,它们除颜色外其余都相同.某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近______;(精确到0.1)
(2)试估算口袋中白球有多少只?
(3)从中先摸出一球,不放回,再摸出一球;请利用树状图或列表计算这两只球颜色不同的概率是多少?
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
单元小结
【详解】(1)当n很大时,摸到白球的频率将会接近0.6;
(2)由(1)摸到白球的概率为0.6,
所以可估计口袋中白种颜色的球的个数=5×0.6=3(只);
单元小结
考点训练七 简单概率的应用问题
单元小结
针对训练
1.如图所示,准备了三张大小相同的纸片,其中两张纸片上各画一个半径相等的半圆,另一张纸片上画一个正方形.将这三张纸片放在一个盒子里摇匀,随机地抽取两张纸片,若可以拼成一个圆形(取出的两张纸片都画有半圆形)则甲方赢;若可以拼成一个蘑菇形(取出的一张纸片画有半圆、一张画有正方形)则乙方赢.你认为这个游戏对双方是公平的吗?若不是,有利于谁? .
单元小结
【详解】解:根据游戏规则可知:从三张大小相同的纸片中随机地抽取两张纸片,共3种情况;
可以拼成一个圆形的有1种;可以拼成一个蘑茹形有2种;
故乙取胜的概率大于甲取胜的概率;
故这个游戏不公平,且对乙有利.
故答案为:不公平,乙有利.
单元小结
2.某校举行“传颂中华家风,弘扬中华美德”演讲比赛.每班选拔一人参加.七年级(1)班的小丽和小华表现都很优秀,现在打算从2位同学中任选1人参加学校演讲比赛.为此设计了如下游戏规则:在一个不透明的袋子里装有10个除号码外其余都相同的小球,小球的号码分别是1,2,3,4,5,6,7,8,9,10.将它们充分摇匀,并从中任意摸出一个小球.规定摸出小球的号码能被3整除时,则小丽去;摸出小球的号码能被5整除时,则小华去.这个游戏对双方公平吗?请说明理由.如果不公平,应该如何修改游戏规则才能对双方公平?(游戏对双方公平的原则是双方获胜的概率相等).
单元小结
谢 谢~
同课章节目录
