2。1等腰三角形（说课）

课件26张PPT。义务教育课程标准实验教科书　
浙江版《数学》八年级上册 温州实验中学 上官光毅教材分析目标分析教法分析过程分析评价分析教材分析目标分析教法分析过程分析评价分析教材分析（一）教材的地位和作用
等腰三角形轴　对　称图形的相似解直角三角形图形的全等延伸应用承上启下教材分析（一）教材的地位和作用
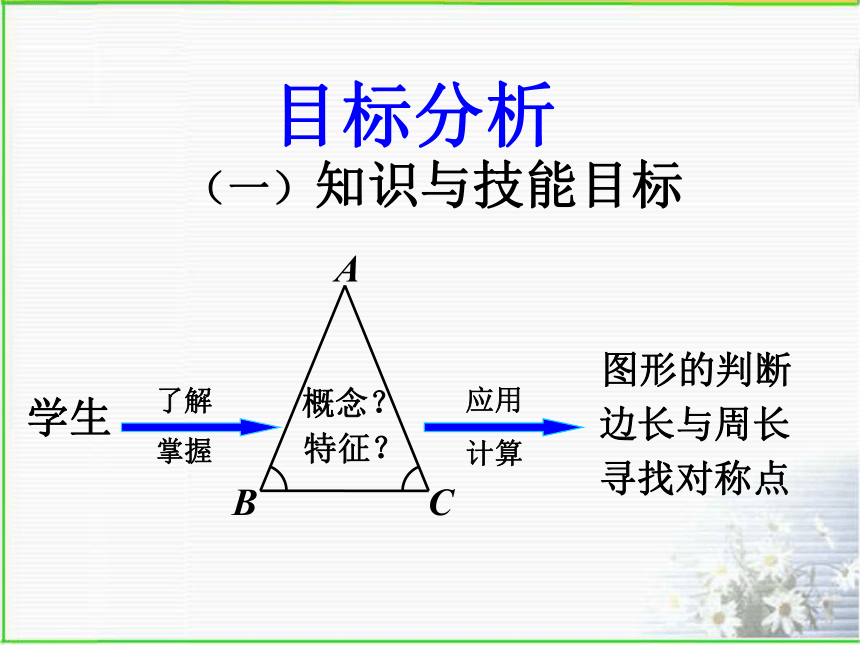
（二）教学的重点和难点重点：等腰三角形的轴对称性． 难点：以等腰三角形的轴对称性为依据来解决点与点,直线与直线的位置关系 . 目标分析（一）知识与技能目标概念？　特征？了解计算应用边长与周长学生掌握寻找对称点图形的判断目标分析（一）知识与技能目标（二）过程与方法目标（三）情感、态度与价值观
培养动手、探索规律及归纳的能力；
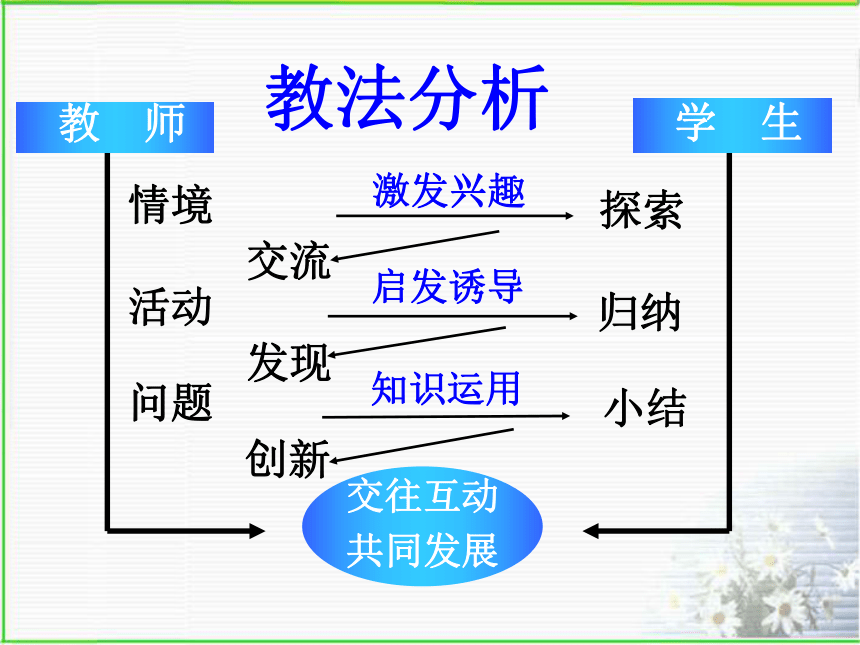
强化分类讨论的思想.　　感受图形中的动态美、和谐美、对称美；　 教　师 学　生情境活动问题探索归纳小结教法分析过程分析折一折,剪一剪材料用具:一张长方形美术纸,一把剪刀⑴先将美术纸对折一次,再剪一刀,请你剪出一个三角形．⑵将剪后的图形展开,同学们所得到三角形有什么特点?设计意图1．借助操作活动感受数学来源与生活的特点，激发兴趣；
２．学生通过观察回顾定义,同时为下面轴对称性的研究埋下伏笔； 定义：两条边相等的三角形叫做等腰三角形.设计意图１．通过生活举例了解等腰三角形在生活中的应用；
２．为下面了解等腰三角形的概念要素作必要的准备．生活举例问题：在我们的生活中，你见到过等腰三角形吗?请举例说明．底边概念介绍　　等腰三角形中，相等的两条边都叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角.设计意图 锻炼学生的表达能力，为等腰三角形的概念应用作好铺垫．设计意图１．在图形中学会根据定义判断等腰三角形；
２．通过改变条件,而不改变图形，达到强化定义本质的目的．概念应用⑴如图,点D在AC上,若AB=AC, AD=BD,你能在图中找出几个等腰三角形?若划线部分的条件改为AD=BD=BC，则结论如何？概念应用设计意图 学会根据腰和底边长作等腰三角形，使学生在动手操作中加深对定义的理解 ．ba⑵已知线段a，b．用直尺和圆规作一个等腰三角形ABC，使AB=AC=b，BC=a．设计意图１．借助实物演示，引导学生通过观察得出结论；
２．回顾轴对称图形的意义，为说明等腰三角形的对称轴作铺垫探索等腰三角形的性质拿出刚开始剪得的等腰三角形，借助实物投影，继续观察：问题1：从剪纸的过程来看，等腰三角形是轴对称图形吗？问题2：轴对称图形的定义是怎么描述的？设计意图 从正逆两个方向来说明顶角平分线所在的直线即为等腰三角形的对称轴，从而得出结论．问题3：你认为等腰三角形的对称轴是什么？问题4：将等腰三角形沿着顶角平分线所在直线对折，直线两侧的部分能重合吗？结论：等腰三角形是
轴对称图形，顶角平
分线所在的直线是它
的对称轴．探索等腰三角形的性质设计意图 给学生充分思考探索的空间，给同学们小组合作的机会，边思考边动手画，从而形成有效的经验与方法．轴对称性质的应用思考1：在AB上取一点D，如何作出点D关于AP的对称点？已知，在△ABC中，AB=AC，AP是△ABC的平分线设计意图 1. 通过直觉猜想与推理验证相结合的方式培养学生思维的严谨性。
2. 进一步小结作垂线的实质是满足了点D、E到顶点A的距离相等．轴对称性质的应用思考1：在AB上取一点D，如何作出点D关于AP的对称点？已知，在△ABC中，AB=AC，AP是△ABC的平分线设计意图 1. 进一步借助轴对称的性质来解决直线与直线的位置关系;

2. 使学生对等腰三角形的轴对称性质有了更具体的认识。
轴对称性质的应用思考2：在AB上再取一点F，作它关于AP的对称点G ，则DE与FG的位置有什么关系 ？已知，在△ABC中，AB=AC，AP是△ABC的平分线它们与底边BC的位置关系又如何呢？设计意图 通过图形的变式及点位置的改变，渗透对称点作法的本质思想。轴对称性质的应用变式：在AC上取点E，BC上取点F，作出它们关于AP的对称点．已知，在△ABC中，AB=AC，AP是△ABC的平分线知识竞赛大比拼（2）等腰三角形的一边长为3，一边长为5，那么它的周长是______（1）等腰三角形的一边长为3，一边长为7，那么它的周长是______11或1317（3）等腰三角形的一边长为4，周长为9，那么它的腰长是________4或2.5设计意图:在等腰三角形的有关边长或周长
的计算中，强化分类讨论思想．我来算一算我来找一找 (1)如图所示的五角星中有___个 等腰三角形． (2) 如图，已知线段AB的一个端点B在直线m上，请你在直线m上找出一点C，使△ABC成为以AB为腰的等腰三角形.C1C2C310 (3) 如图，正方形上给定8个点，以这些点为顶点，能构成多少个等腰三角形.AB4×34×2设计意图:设置不同类型的找等腰三角形的问
题，使学生在探索过程中逐步形成规律，并
体会分类讨论思想的重要性．让我来判断 已知，在下列图形中，AB=AC，AP是△ABC的平分线，请判断图中的D、E是否关于AP对称？PD⊥AB ， PE⊥AC设计意图:考查学生对等腰三角形轴对称性的理解
,还注重了对学生推理能力的要求．作业布置(分层) (1)完成课后作业题． (2)作业本相应内容．⑶思考课本中的探究活动: 通过摆火柴体验三角形三边关系的应用.实践探索感受特征回顾小结整体感知 变式练习拓展提高创设情景激发兴趣回顾概念引出新知布置作业巩固加深教学流程 发生形成发展