浙教版数学八年级上册 2.8直角三角形全等的判定 课件(共22张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 2.8直角三角形全等的判定 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 265.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 13:03:28 | ||
图片预览






文档简介
(共22张PPT)
第2章 特殊三角形
2.8 直角三角形全等的判定
学习目标
一
探索两个直角三角形全等的条件.
掌握两个直角三角形全等的判定定理(HL):斜边和一条直角边对应相等的两个直角三角形全等.
探索并证明角平分线性质定理的逆定理.
①
②
③
情境导入
二
三条道路两两相交,你能找出一点,使它到三条道路的距离都相等吗?
合作探究
三
回顾:要判定两个三角形全等,我们已经有哪些方法?
ASA
AAS
SAS
SSS
活动探究:
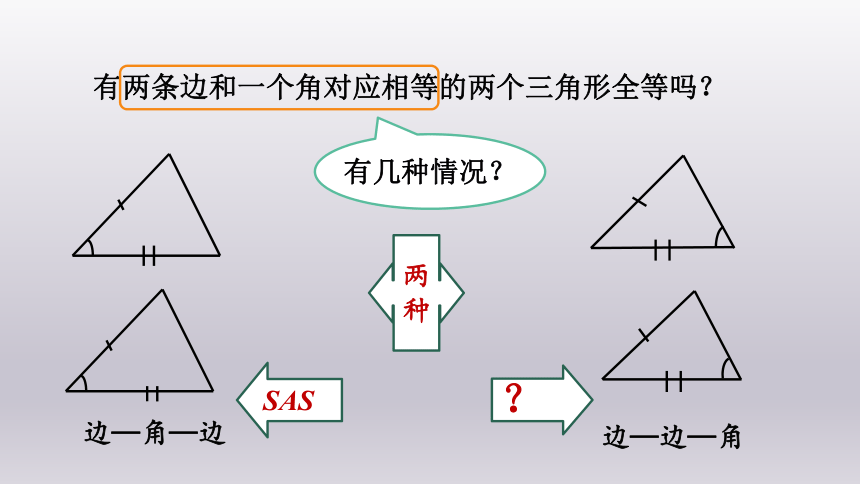
(1)有两条边和一个角对应相等的两个三角形全等吗?
(2)如果这个角是直角呢?
可通过作图、叠合等方法进行探索.
有两条边和一个角对应相等的两个三角形全等吗?
有几种情况?
边—角—边
两种
边—边—角
SAS
?
A
45°
B′
B
C
5cm
4cm
4cm
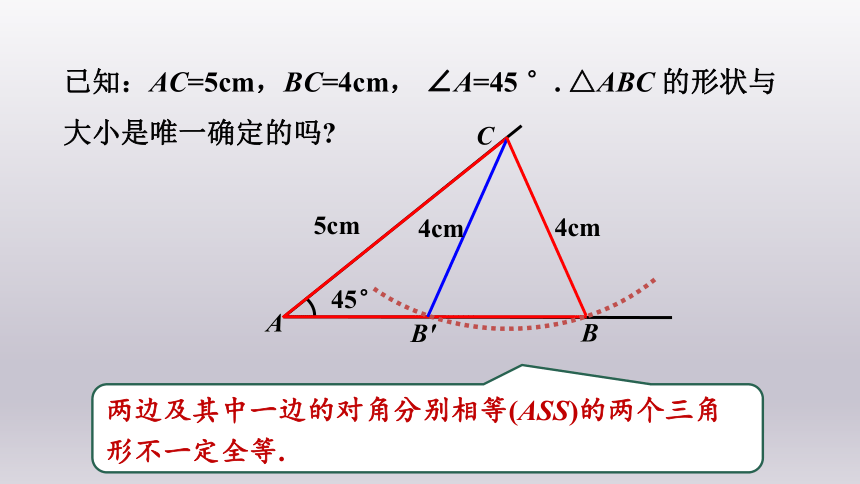
已知:AC=5cm,BC=4cm, ∠A=45 °. △ABC 的形状与大小是唯一确定的吗
两边及其中一边的对角分别相等(ASS)的两个三角形不一定全等.
两边及其中一边的对角分别相等(ASS)的两个三角形不一定全等.
如果这个角是直角呢?
实际上,根据勾股定理,已知直角三角形的两边长即可得出第三边的长.然后根据SSS即可判定全等.
归纳新知
四
斜边和一条直角边分别相等的两个直角三角形全等.
(可以简写成“斜边直角边”或“HL”).
直角三角形全等的判定定理
除了利用勾股定理,你还有其他证明这个定理的方法吗?
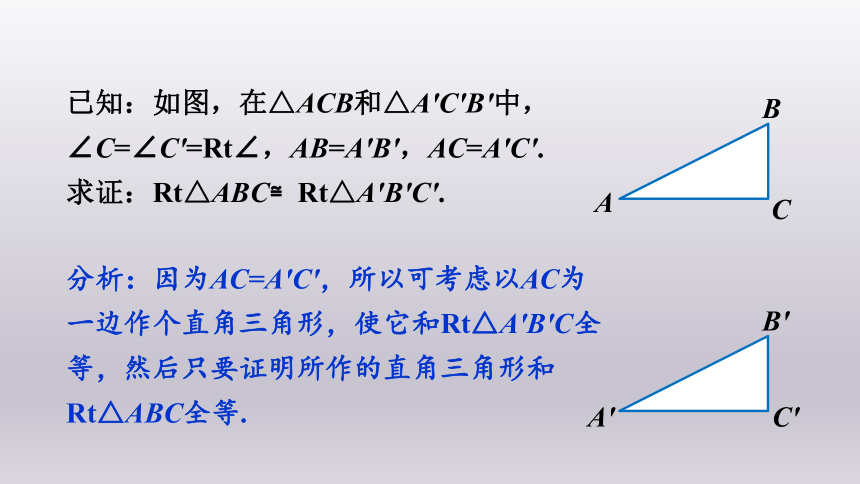
已知:如图,在△ACB和△A′C′B′中,∠C=∠C′=Rt∠,AB=A′B′,AC=A′C′.
求证:Rt△ABC≌Rt△A′B′C′.
分析:因为AC=A′C′,所以可考虑以AC为一边作个直角三角形,使它和Rt△A′B′C全等,然后只要证明所作的直角三角形和Rt△ABC全等.
C
A
B
C′
A′
B′
证明:如图,延长BC至D,使CD=B′C′,连结AD.
∵AC=A′C′ (已知),∠ACD=Rt∠=∠C′,
∴ △ADC≌△A′B′C′ (SAS).
∴AD=A′B′ (全等三角形的对应边相等).
∵ A′B′=AB (已知) ,
又∵AC⊥BD,
∴BC=DC (等腰三角形三线合一).
而AC=AC (公共边) ,
∴△ADC≌△ABC (SSS) ,
C
A
B
C′
A′
B′
D
∴△ABC≌△A′B′C′.
∴ AD=AB.
做一做
五
已知线段a,c(如图),用直尺和圆规作Rt△ABC,使∠C=Rt∠,BC=a,AB=c.
a
c
作法:1.画∠MCN=90°;
2.在射线CM上取BC=a ;
3.以B为圆心,c为半径画弧,交射线CN于点A;
4.连接AB.
则△ ABC就是所求作三角形.
a
c
M
C
N
B
A
经典例题
六
例 已知:如图,P是∠AOB内一点PD⊥OA,PE⊥OB , D,E分别是垂足,且PD=PE.
求证:点P在∠AOB的平分线上.
A
O
B
D
E
P
分析:如图,要证明点P在∠AOB的平分线上,可以转化为证明射线OP平分∠AOB.
证明:如图,作射线OP.
∵PD⊥OA,PE⊥OB (已知),
∴∠PDO=∠PEO=Rt∠.
又∵ OP=OP (公共边),PD=PE (已知) ,
∴Rt△PDO≌Rt△PEO (HL).
∴ ∠AOP=∠BOP ,
即点P在∠AOB的平分线上(角平分线的定义).
A
O
B
D
E
P
你发现了什么规律?
发现总结
七
角的内部,到角两边距离相等的点,在这个角的平分线上.
角平分线性质定理的逆定理
这个定理的逆定理是:_______________________________,
即____________________.
角平分线上的点到角两边距离相等
角平分线的性质定理
情境回顾
八
三条道路两两相交,你能找出一点,使它到三条道路的距离都相等吗?
①分别画出三个角的角平分线;
②根据“角的内部,到角两边距离相等的点,在这个角的平分线上”可知交点P到三条道路的距离都相等.
P
随堂练习
九
1.如图,AC=BC,AC⊥OA,CB⊥OB,则Rt△AOC≌Rt△BOC的理由是( )
A.SSS B.ASA
C.SAS D.HL
D
分析:在Rt△AOC和Rt△BOC中,
AC=BC,OC=OC,
则Rt△AOC≌Rt△BOC(HL).
2.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
C
3.在△ABC中,BD=CD,DE⊥AB于点E ,DF⊥AC于点F ,且DE=DF,求证:△BED≌△CFD.
A
B
C
D
E
F
证明:∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°.
∴△DEB和△DFC是直角三角形.
∴Rt△DEB≌Rt△DFC(HL).
∵ DB=DC,DE=DF,
4.已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.求证:PA平分∠MAN.
证明:作PD⊥BC于点D,
∵BP是△ABC的外角平分线,PM⊥AB,PD⊥BC,
∴PM=PD,
同理,PN=PD,
∴PM=PN,
又∵ PM⊥AB,PN⊥AC,
D
∴PA平分∠MAN.
课堂小结
十
(1)叙述两个直角三角形全等的判定定理.
(2)叙述角平分线性质定理的逆定理.
(3)举例说明角平分线性质定理的逆定理在实际生活中的应用.
感谢观看!
第2章 特殊三角形
2.8 直角三角形全等的判定
学习目标
一
探索两个直角三角形全等的条件.
掌握两个直角三角形全等的判定定理(HL):斜边和一条直角边对应相等的两个直角三角形全等.
探索并证明角平分线性质定理的逆定理.
①
②
③
情境导入
二
三条道路两两相交,你能找出一点,使它到三条道路的距离都相等吗?
合作探究
三
回顾:要判定两个三角形全等,我们已经有哪些方法?
ASA
AAS
SAS
SSS
活动探究:
(1)有两条边和一个角对应相等的两个三角形全等吗?
(2)如果这个角是直角呢?
可通过作图、叠合等方法进行探索.
有两条边和一个角对应相等的两个三角形全等吗?
有几种情况?
边—角—边
两种
边—边—角
SAS
?
A
45°
B′
B
C
5cm
4cm
4cm
已知:AC=5cm,BC=4cm, ∠A=45 °. △ABC 的形状与大小是唯一确定的吗
两边及其中一边的对角分别相等(ASS)的两个三角形不一定全等.
两边及其中一边的对角分别相等(ASS)的两个三角形不一定全等.
如果这个角是直角呢?
实际上,根据勾股定理,已知直角三角形的两边长即可得出第三边的长.然后根据SSS即可判定全等.
归纳新知
四
斜边和一条直角边分别相等的两个直角三角形全等.
(可以简写成“斜边直角边”或“HL”).
直角三角形全等的判定定理
除了利用勾股定理,你还有其他证明这个定理的方法吗?
已知:如图,在△ACB和△A′C′B′中,∠C=∠C′=Rt∠,AB=A′B′,AC=A′C′.
求证:Rt△ABC≌Rt△A′B′C′.
分析:因为AC=A′C′,所以可考虑以AC为一边作个直角三角形,使它和Rt△A′B′C全等,然后只要证明所作的直角三角形和Rt△ABC全等.
C
A
B
C′
A′
B′
证明:如图,延长BC至D,使CD=B′C′,连结AD.
∵AC=A′C′ (已知),∠ACD=Rt∠=∠C′,
∴ △ADC≌△A′B′C′ (SAS).
∴AD=A′B′ (全等三角形的对应边相等).
∵ A′B′=AB (已知) ,
又∵AC⊥BD,
∴BC=DC (等腰三角形三线合一).
而AC=AC (公共边) ,
∴△ADC≌△ABC (SSS) ,
C
A
B
C′
A′
B′
D
∴△ABC≌△A′B′C′.
∴ AD=AB.
做一做
五
已知线段a,c(如图),用直尺和圆规作Rt△ABC,使∠C=Rt∠,BC=a,AB=c.
a
c
作法:1.画∠MCN=90°;
2.在射线CM上取BC=a ;
3.以B为圆心,c为半径画弧,交射线CN于点A;
4.连接AB.
则△ ABC就是所求作三角形.
a
c
M
C
N
B
A
经典例题
六
例 已知:如图,P是∠AOB内一点PD⊥OA,PE⊥OB , D,E分别是垂足,且PD=PE.
求证:点P在∠AOB的平分线上.
A
O
B
D
E
P
分析:如图,要证明点P在∠AOB的平分线上,可以转化为证明射线OP平分∠AOB.
证明:如图,作射线OP.
∵PD⊥OA,PE⊥OB (已知),
∴∠PDO=∠PEO=Rt∠.
又∵ OP=OP (公共边),PD=PE (已知) ,
∴Rt△PDO≌Rt△PEO (HL).
∴ ∠AOP=∠BOP ,
即点P在∠AOB的平分线上(角平分线的定义).
A
O
B
D
E
P
你发现了什么规律?
发现总结
七
角的内部,到角两边距离相等的点,在这个角的平分线上.
角平分线性质定理的逆定理
这个定理的逆定理是:_______________________________,
即____________________.
角平分线上的点到角两边距离相等
角平分线的性质定理
情境回顾
八
三条道路两两相交,你能找出一点,使它到三条道路的距离都相等吗?
①分别画出三个角的角平分线;
②根据“角的内部,到角两边距离相等的点,在这个角的平分线上”可知交点P到三条道路的距离都相等.
P
随堂练习
九
1.如图,AC=BC,AC⊥OA,CB⊥OB,则Rt△AOC≌Rt△BOC的理由是( )
A.SSS B.ASA
C.SAS D.HL
D
分析:在Rt△AOC和Rt△BOC中,
AC=BC,OC=OC,
则Rt△AOC≌Rt△BOC(HL).
2.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
C
3.在△ABC中,BD=CD,DE⊥AB于点E ,DF⊥AC于点F ,且DE=DF,求证:△BED≌△CFD.
A
B
C
D
E
F
证明:∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°.
∴△DEB和△DFC是直角三角形.
∴Rt△DEB≌Rt△DFC(HL).
∵ DB=DC,DE=DF,
4.已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.求证:PA平分∠MAN.
证明:作PD⊥BC于点D,
∵BP是△ABC的外角平分线,PM⊥AB,PD⊥BC,
∴PM=PD,
同理,PN=PD,
∴PM=PN,
又∵ PM⊥AB,PN⊥AC,
D
∴PA平分∠MAN.
课堂小结
十
(1)叙述两个直角三角形全等的判定定理.
(2)叙述角平分线性质定理的逆定理.
(3)举例说明角平分线性质定理的逆定理在实际生活中的应用.
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
