浙教版数学八年级上册 5.5.2 一次函数与二元一次方程组课件(共23张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 5.5.2 一次函数与二元一次方程组课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 778.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 16:15:52 | ||
图片预览




文档简介
(共23张PPT)
5.5 一次函数的简单应用
第2课时 一次函数与二元一次方程组
学习目标
体会一次函数与二元一次方程(组)的关系.
掌握二元一次方程组和对应的两直线之间的关系.
会根据图象求二元一次方程组的近似解.
新知引入
1.把二元一次方程 x+y=3 改写成用含x的式子表示y:_______.
3.以方程 x+y=3 的解为坐标的所有点在一条直线上吗?如果在一条直线上,它们在哪条直线上?
y=-x +3
2.二元一次方程 x+y=3 有______组解,写出其中几组.
无数
x=4
y=-1
x=3
y=0
x=2
y=1
合作探究
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
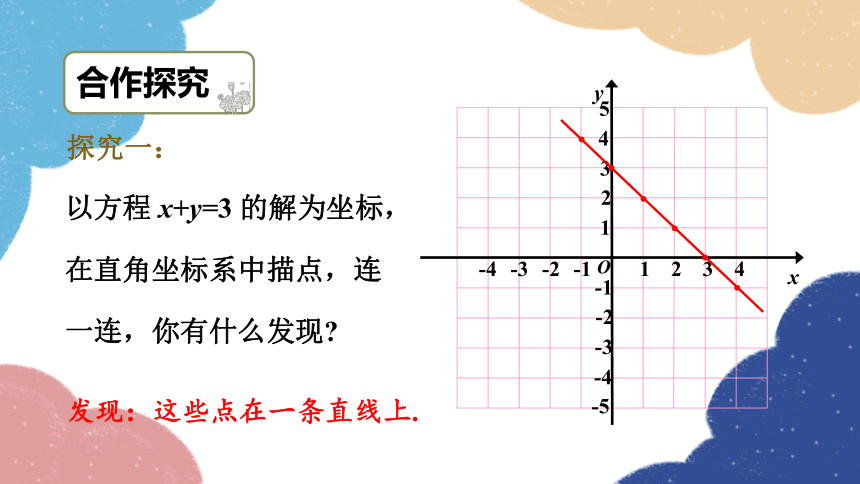
以方程 x+y=3 的解为坐标,在直角坐标系中描点,连一连,你有什么发现
发现:这些点在一条直线上.
探究一:
合作探究
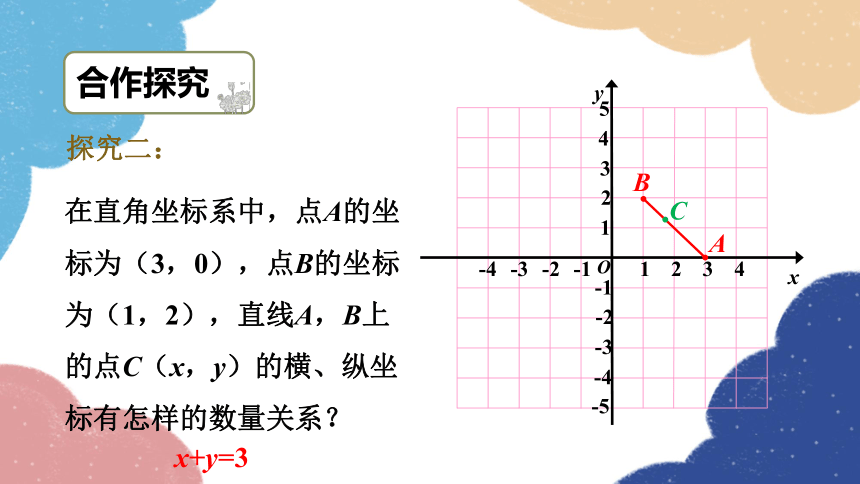
在直角坐标系中,点A的坐标为(3,0),点B的坐标为(1,2),直线A,B上的点C(x,y)的横、纵坐标有怎样的数量关系?
探究二:
x+y=3
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
A
B
C
合作探究
综合探究一、探究二,你得出什么结论
以方程 ax+by=c 的解为坐标的点在一条直线上.
反之,以这个方程的两组解为坐标画出的直线,此直线上的点的坐标组成的一组值是这个二元一次方程的一组解.
因此,以二元一次方程的解为坐标的点在一条直线上.
合作探究
探究三:
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
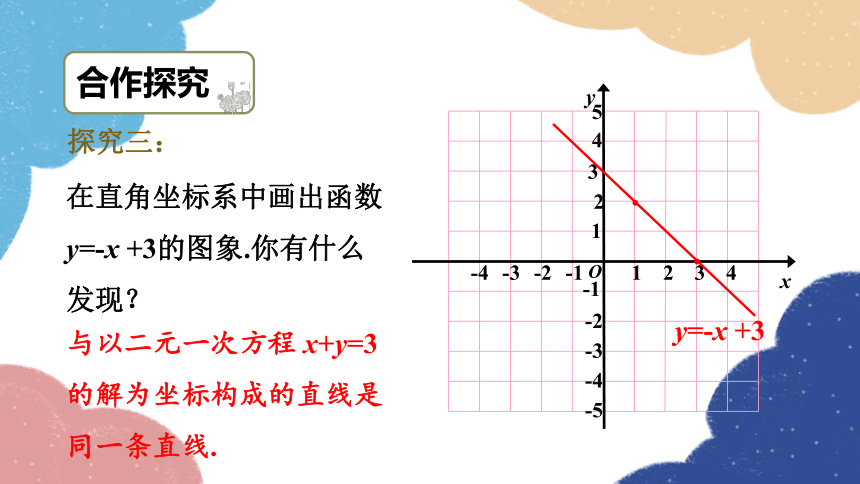
在直角坐标系中画出函数y=-x +3的图象.你有什么发现?
y=-x +3
与以二元一次方程 x+y=3 的解为坐标构成的直线是同一条直线.
合作探究
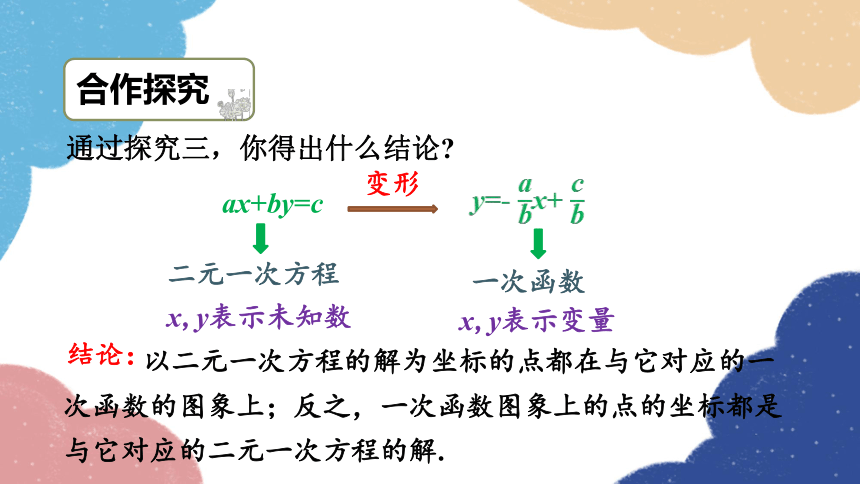
通过探究三,你得出什么结论
ax+by=c
变形
二元一次方程
x,y表示未知数
一次函数
x,y表示变量
结论:
以二元一次方程的解为坐标的点都在与它对应的一次函数的图象上;反之,一次函数图象上的点的坐标都是与它对应的二元一次方程的解.
合作探究
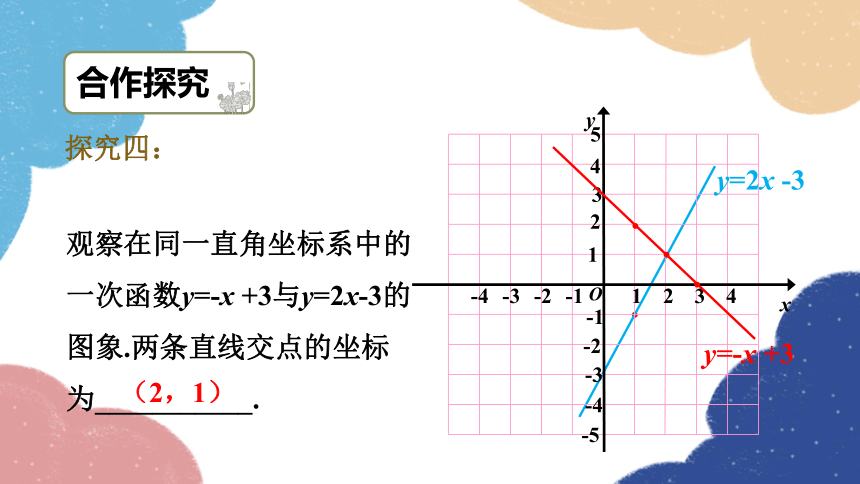
探究四:
观察在同一直角坐标系中的一次函数y=-x +3与y=2x-3的图象.两条直线交点的坐标为___________.
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=-x +3
y=2x -3
(2,1)
合作探究
一次函数y=-x +3与y=2x-3的对应的方程组成的方程组
的解为____________.
以二元一次方程组的解为坐标的点就是与它们对应的两个一次函数的图象上的交点;反过来,两个一次函数图象上的交点的坐标就是与它对应的二元一次方程组的解.
发现:
典例精讲
例1 解方程组 并由此指出在同一直角坐标系
内,一次函数y=2x-2与y=-2x+6图象交点的坐标.
解:
一次函数y=2x-2与y=-2x+6图象交点的坐标为(2,2).
例2 我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶(左图).右图中 l1 ,l2 分别表示两船相对于海岸的距离s(n mile)与追赶时间t(min)之间的关系.根据图象回答下列问题:
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
(1)哪条线表示 B 到海岸距离与追赶时间之间的关系?
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
当t=0时,B距海岸0n mile,
即s=0,
故l1 表示 B 到海岸的距离与追赶时间之间的关系.
(2)A、B 哪个速度快?
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
t从0增加到10时,l2的纵坐标
增加了2,l1的纵坐标增加了5,
即10 min内,A 行驶了 2 n mile,
B 行驶了5 n mile,
所以 B 的速度快.
(3)15min内 B 能否追上 A?
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
12
14
16
延长l1,l2,
可以看出,当t=15时,l1上
对应点在l2上对应点的下方.
这表明,15 min时B尚未追
上A.
(4)如果一直追下去,那么B能否追上 A?
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
12
14
16
P
因此,如果一直追下去,
那么 B 一定能追上 A.
(5)当A逃到离海岸12n mile的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截?
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
12
14
16
10
12
P
从图中可以看出,l1 与 l2 交点
P的纵坐标小于12,
这说明在 A 逃入公海前,我边
防快艇 B能够追上 A.
(6)l1与l2对应的两个一次函数s=k1x+b1与s=k2x+b2中,k1,k2的实际意义各是什么?可疑船只A与快艇B的速度各是多少?
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
12
14
16
k1表示快艇B的速度,
k2表示可疑船只A的速度.
可疑船只A的速度是0.2 n
mile/min,
快艇B的速度是0.5 n mile/min.
随堂练习
2.若二元一次方程组 的解为 ,则函数y=
x+1与y=2x-2的图象的交点坐标为________.
1.已知一次函数 y =3x-1与y=2x图象的交点是(1,2),则方程组 的解为_______.
3x-y=1
2x-y=0
(2,2)
x-2y=-2
2x-y=2
x=2
y=2
x=1
y=2
随堂练习
3.甲、乙两地相距300千米,一辆货车和一辆轿车分别从甲地开往乙地(轿车的平均速度大于货车的平均速度),如图线段OA和折线BCD分别表示两车离甲地的距离y(单位:千米)与时间x(单位:小时)之间的函数关系.则下列说法正确的是( )
A.两车同时到达乙地
B.轿车在行驶过程中进行了提速
C.货车出发3小时后,轿车追上货车
D.两车在前80千米的速度相等
B
O
2.5
5
x/小时
y/千米
80
300
1.2
4.5
A
D
C
B
随堂练习
o
-2
1
-2
1
3
2x+y=4
2x-3y=12
4.用图象法解方程组:
①
②
作出图象:
观察图象,得交点(3,-2)
所以方程组的解为
x=3.
y=-2.
y=-2x+4
解:
由①,得y=-2x+4
课堂小结
对应关系
① 将方程组中各方程化为y=kx+b的形式;
② 画出各个一次函数的图象;
③ 由交点坐标得出方程组的解.
二元一次方程组的解
两个一次函数图象的交点坐标
图象法解方程组的步骤:
感谢观看!
5.5 一次函数的简单应用
第2课时 一次函数与二元一次方程组
学习目标
体会一次函数与二元一次方程(组)的关系.
掌握二元一次方程组和对应的两直线之间的关系.
会根据图象求二元一次方程组的近似解.
新知引入
1.把二元一次方程 x+y=3 改写成用含x的式子表示y:_______.
3.以方程 x+y=3 的解为坐标的所有点在一条直线上吗?如果在一条直线上,它们在哪条直线上?
y=-x +3
2.二元一次方程 x+y=3 有______组解,写出其中几组.
无数
x=4
y=-1
x=3
y=0
x=2
y=1
合作探究
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
以方程 x+y=3 的解为坐标,在直角坐标系中描点,连一连,你有什么发现
发现:这些点在一条直线上.
探究一:
合作探究
在直角坐标系中,点A的坐标为(3,0),点B的坐标为(1,2),直线A,B上的点C(x,y)的横、纵坐标有怎样的数量关系?
探究二:
x+y=3
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
A
B
C
合作探究
综合探究一、探究二,你得出什么结论
以方程 ax+by=c 的解为坐标的点在一条直线上.
反之,以这个方程的两组解为坐标画出的直线,此直线上的点的坐标组成的一组值是这个二元一次方程的一组解.
因此,以二元一次方程的解为坐标的点在一条直线上.
合作探究
探究三:
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
在直角坐标系中画出函数y=-x +3的图象.你有什么发现?
y=-x +3
与以二元一次方程 x+y=3 的解为坐标构成的直线是同一条直线.
合作探究
通过探究三,你得出什么结论
ax+by=c
变形
二元一次方程
x,y表示未知数
一次函数
x,y表示变量
结论:
以二元一次方程的解为坐标的点都在与它对应的一次函数的图象上;反之,一次函数图象上的点的坐标都是与它对应的二元一次方程的解.
合作探究
探究四:
观察在同一直角坐标系中的一次函数y=-x +3与y=2x-3的图象.两条直线交点的坐标为___________.
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=-x +3
y=2x -3
(2,1)
合作探究
一次函数y=-x +3与y=2x-3的对应的方程组成的方程组
的解为____________.
以二元一次方程组的解为坐标的点就是与它们对应的两个一次函数的图象上的交点;反过来,两个一次函数图象上的交点的坐标就是与它对应的二元一次方程组的解.
发现:
典例精讲
例1 解方程组 并由此指出在同一直角坐标系
内,一次函数y=2x-2与y=-2x+6图象交点的坐标.
解:
一次函数y=2x-2与y=-2x+6图象交点的坐标为(2,2).
例2 我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶(左图).右图中 l1 ,l2 分别表示两船相对于海岸的距离s(n mile)与追赶时间t(min)之间的关系.根据图象回答下列问题:
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
(1)哪条线表示 B 到海岸距离与追赶时间之间的关系?
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
当t=0时,B距海岸0n mile,
即s=0,
故l1 表示 B 到海岸的距离与追赶时间之间的关系.
(2)A、B 哪个速度快?
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
t从0增加到10时,l2的纵坐标
增加了2,l1的纵坐标增加了5,
即10 min内,A 行驶了 2 n mile,
B 行驶了5 n mile,
所以 B 的速度快.
(3)15min内 B 能否追上 A?
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
12
14
16
延长l1,l2,
可以看出,当t=15时,l1上
对应点在l2上对应点的下方.
这表明,15 min时B尚未追
上A.
(4)如果一直追下去,那么B能否追上 A?
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
12
14
16
P
因此,如果一直追下去,
那么 B 一定能追上 A.
(5)当A逃到离海岸12n mile的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截?
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
12
14
16
10
12
P
从图中可以看出,l1 与 l2 交点
P的纵坐标小于12,
这说明在 A 逃入公海前,我边
防快艇 B能够追上 A.
(6)l1与l2对应的两个一次函数s=k1x+b1与s=k2x+b2中,k1,k2的实际意义各是什么?可疑船只A与快艇B的速度各是多少?
O
t/min
s/n mile
8
1
4
10
2
2
3
4
5
6
6
l2
l1
7
8
12
14
16
k1表示快艇B的速度,
k2表示可疑船只A的速度.
可疑船只A的速度是0.2 n
mile/min,
快艇B的速度是0.5 n mile/min.
随堂练习
2.若二元一次方程组 的解为 ,则函数y=
x+1与y=2x-2的图象的交点坐标为________.
1.已知一次函数 y =3x-1与y=2x图象的交点是(1,2),则方程组 的解为_______.
3x-y=1
2x-y=0
(2,2)
x-2y=-2
2x-y=2
x=2
y=2
x=1
y=2
随堂练习
3.甲、乙两地相距300千米,一辆货车和一辆轿车分别从甲地开往乙地(轿车的平均速度大于货车的平均速度),如图线段OA和折线BCD分别表示两车离甲地的距离y(单位:千米)与时间x(单位:小时)之间的函数关系.则下列说法正确的是( )
A.两车同时到达乙地
B.轿车在行驶过程中进行了提速
C.货车出发3小时后,轿车追上货车
D.两车在前80千米的速度相等
B
O
2.5
5
x/小时
y/千米
80
300
1.2
4.5
A
D
C
B
随堂练习
o
-2
1
-2
1
3
2x+y=4
2x-3y=12
4.用图象法解方程组:
①
②
作出图象:
观察图象,得交点(3,-2)
所以方程组的解为
x=3.
y=-2.
y=-2x+4
解:
由①,得y=-2x+4
课堂小结
对应关系
① 将方程组中各方程化为y=kx+b的形式;
② 画出各个一次函数的图象;
③ 由交点坐标得出方程组的解.
二元一次方程组的解
两个一次函数图象的交点坐标
图象法解方程组的步骤:
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
