6.5角与角的度量

课件28张PPT。第六章 图形的初步知识§6.5 角与角的度量课前 · 预学区本课目标预习填空基础自测温故知新自主学习　基础落实 1. 能从生活实例中抽象出角．
2. 会用不同的方法表示一个角．
3. 掌握度、分、秒单位及其换算．课前 · 预学区自主学习　基础落实 本课目标预习填空温故知新由两条有公共端点的射线所组成的图形叫做角．
你能举出生活中角的例子吗？略基础自测课前 · 预学区自主学习　基础落实 本课目标预习填空温故知新 ___________是角的基本度量单位．一个直角等于
______°，一个平角等于______°，一个周角等于
______°.
2. 1度______分，1分＝______秒，1度＝_______秒．3600度、分、秒901803606060基础自测课前 · 预学区自主学习　基础落实 本课目标预习填空温故知新1. 角是由两条有公共_______的_______所组成的图形．
2. 角的符号用______表示，请用三种不同方法表示下图
中的角：________________________．端点射线∠∠O、∠AOB、∠1基础自测课前 · 预学区自主学习　基础落实 本课目标预习填空温故知新3. 用“度、分、秒”表示18.5°＝________．
4. 用“度”表示30°18′＝________．
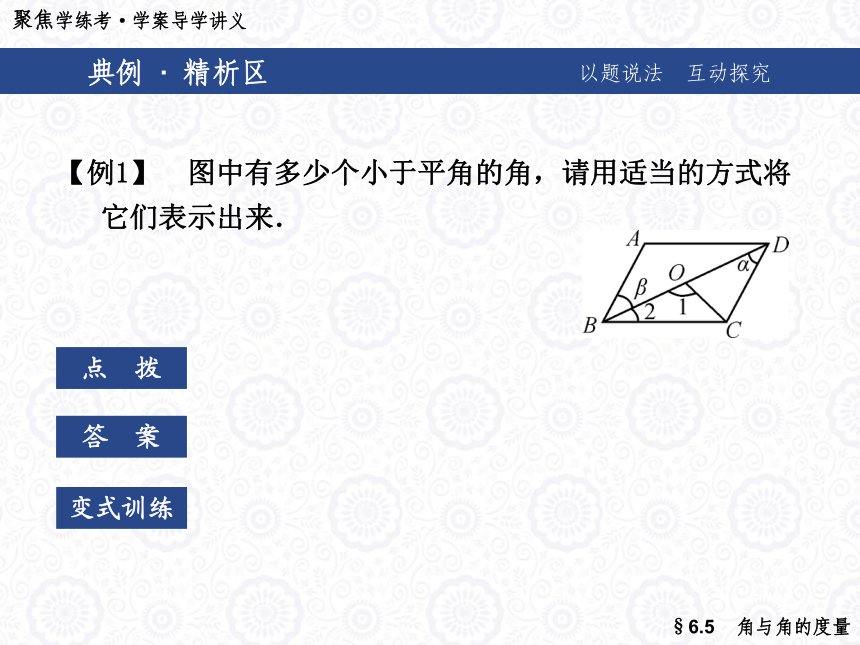
5. 计算：21°25′14″＋17°18′30″＝________．38°43′44″18°30′30.3°基础自测典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例1】　图中有多少个小于平角的角，请用适当的方式将
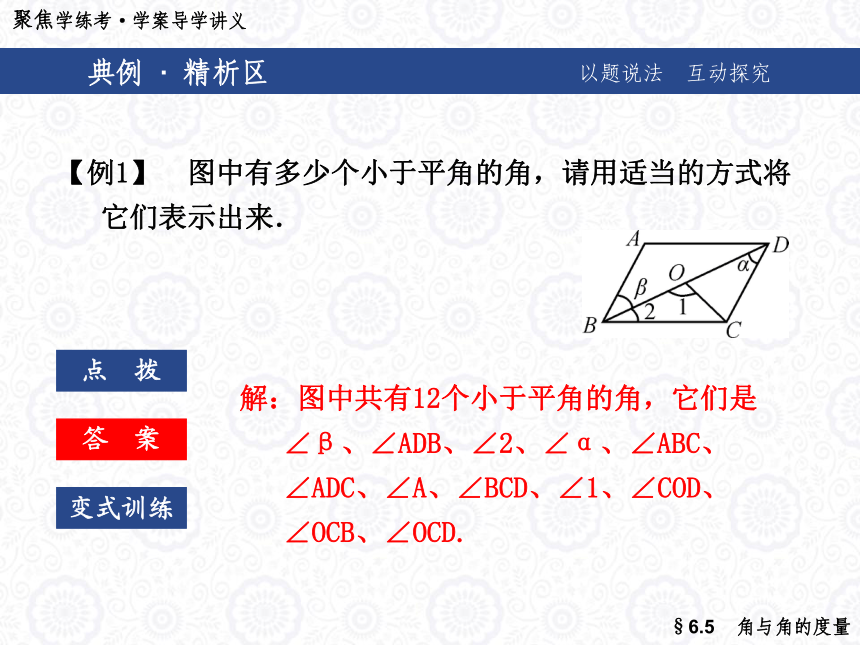
它们表示出来．典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例1】　图中有多少个小于平角的角，请用适当的方式将
它们表示出来．注意角的不同表示方法，当以一点为顶点
的角只有一个的时候，这个角才可以用一
个大写字母表示．典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例1】　图中有多少个小于平角的角，请用适当的方式将
它们表示出来．解：图中共有12个小于平角的角，它们是
∠β、∠ADB、∠2、∠α、∠ABC、
∠ADC、∠A、∠BCD、∠1、∠COD、
∠OCB、∠OCD.典例 · 精析区以题说法　互动探究变式训练1　
如图，其中能用一个大写字母表示的角有________个．2 典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例2】　“角”的单位互换：
(1)50.22°＝______°______′______″.
(2)32°14′24″＝______°.典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例2】　“角”的单位互换：
(1)50.22°＝______°______′______″.
(2)32°14′24″＝______°.将大的单位化为小的单位用乘法，
反之用除法．典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例2】　“角”的单位互换：
(1)50.22°＝______°______′______″.
(2)32°14′24″＝_________°.50131232.24典例 · 精析区以题说法　互动探究【例2】　“角”的单位互换：
(1)50.22°＝______°______′______″.
(2)32°14′24″＝_________°.50131232.242. 某校八年级在下午3∶30开展“阳光
体育”活动，则这一时刻，时钟上分
针与时针所夹的角等于________．　75°点 拨答 案变式训练典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例3】　如图a，当∠AOB内部有一条射线时，图中共有3个
角；如图b，当∠AOB内部有两条射线时，图中共有6个角；
如图c，当∠AOB内部有三条射线时，图中共有多少个角？
如果∠AOB内部有n条射线呢？典例 · 精析区以题说法　互动探究【例3】　如图a，当∠AOB内部有一条射线时，图中共有3个
角；如图b，当∠AOB内部有两条射线时，图中共有6个角；
如图c，当∠AOB内部有三条射线时，图中共有多少个角？
如果∠AOB内部有n条射线呢？本题是一道规律的探索题，当∠AOB内部有一条射
线时，共有角1＋2＝3个；当∠AOB内部有两条射
线时，共有角1＋2＋3＝6个，那么当∠AOB内部有
三条射线时，共有角1＋2＋3＋4＝10个．从中你
发现了什么规律？点 拨答 案变式训练典例 · 精析区以题说法　互动探究【例3】　如图a，当∠AOB内部有一条射线时，图中共有3个
角；如图b，当∠AOB内部有两条射线时，图中共有6个角；
如图c，当∠AOB内部有三条射线时，图中共有多少个角？
如果∠AOB内部有n条射线呢？解：当有1条射线时，角共有：1＋2＝3(个)；
当有2条射线时，角共有：1＋2＋3＝6(个)；
当有3条射线时，角共有：1＋2＋3＋4＝10(个)；
…
当有n条射线时，角共有：点 拨答 案变式训练典例 · 精析区以题说法　互动探究变式训练3　上题图中，若∠AOB内部有n条射线，能否使
得图中共有2013个角？若能，求出n的值；若不能，请
说明理由．则(n＋1)(n＋2)＝4026，找不到两个连续整数的
积为4026，所以不能．归纳总结 角不是射线，它的两个定义是从不同角度去概括的，
但共同之处是：角是一种“图形”．
2. 角的度、分、秒换算与时间的时、分、秒换算是一
样的，都是60进制，不要认为是100进制．
3. 在做角度相加减时，度与度、分与分、秒与秒分别
相加减，当结果中的“秒”或“分”超过60时，分
逐级由秒向分转化，再由分向度转化，当被减数中
的“秒”不够减时，要向“分”借，1′当60″用；
当“分”不够减时，要向“度”借，1°当60′用．随堂 · 检测区即时演练　查漏补缺 A. 基础部分（共8题，每题10分） (一)选择题
下列四个图中，能用∠1，∠AOB，∠O三种方法表示
同一个角的图是 (　　)B随堂 · 检测区即时演练　查漏补缺 2. 下列说法中，正确的是 (　　)
A. 角可以看作是由一条射线绕着它的端点旋转
而成的图形
B. 角的边越长，角越大
C. 两条射线组成的图形叫做角
D. 直线的度数是180°A随堂 · 检测区即时演练　查漏补缺 3. 下列各角中是钝角的是 (　　)A随堂 · 检测区即时演练　查漏补缺 4. 9∶30时，分针与时针的夹角度数是 (　　)
A. 90° B. 105°
C. 135° D. 120°B随堂 · 检测区即时演练　查漏补缺 (二)填空题
5. ∠A＝21.3°，∠B＝21°3′，则∠A与∠B的大小关系
是__________．
6. 如图，∠AOB＝108°，∠BOC＝35°25′，则∠AOC的
度数是__________．
7. 把78.5°化为度、分、秒的形式为__________．78°30′　 ∠A＞∠B72°35′随堂 · 检测区即时演练　查漏补缺 (三)解答题
8. 如图，∠AOB＝42°15′.
(1)作∠COB，使∠COB是直角；
(2)求∠AOC的角度数．解：(1)略　
(2)132°15′或47°45′　 随堂 · 检测区即时演练　查漏补缺 B. 提高部分（共2题，每题10分） 9. 如图，在AB上任取一点D，在BC上任取一点E，得
∠DBE；又在BA、BC的延长线上任取一点F、G，得
到∠FBG.问：∠DBE，∠ABC，∠FBG所表示的是同
一个角吗？这一事实说明了什么？解：∠DBE、∠ABC、∠FBG表示同
一个角．
这一事实说明：角的边是射线． 随堂 · 检测区即时演练　查漏补缺 10. 如图，若∠α∶∠β∶∠γ＝1∶2∶4，∠δ＝73°，
求∠α、∠β的度数．解：∵∠α∶∠β∶∠γ＝1∶2∶4，
∴∠β＝2∠α，∠γ＝4∠α，
∴∠α＋2∠α＋4∠α＋73°＝360°，
解得：∠α＝41°，
∴∠β＝2∠α＝82°.随堂 · 检测区即时演练　查漏补缺 C. 头脑风暴（选做题，20分） 11. (1)现有一个19°的模板，请设计一种办法，只有这个
模板和铅笔在纸上画出1°的角．
(2)现有一个17°的模板和铅笔，你能画出1°的角吗？
(3)如果是21°的模板，能画出1°的
角吗？为什么？解：(1)19个19°为361°，去掉360°的周角，得到1°角．　
(2)53个17°为901°，去掉两个360°和一个180°即可
得1°角．　
(3)当模板为21°时，方程21x－180y＝1无整数解，
∴不能利用21°模板画出1°角．