6.9直线的相交(第1课时)

课件25张PPT。第六章 图形的初步知识§6.9 直线的相交
（第1课时）课前 · 预学区本课目标预习填空基础自测温故知新自主学习　基础落实 1. 了解相交线和对顶角的概念．
2. 理解“对顶角相等”这一重要性质．
3. 会综合这用余角、补角、角平分线和对顶角的
性质进行有关角的计算．课前 · 预学区自主学习　基础落实 本课目标温故知新基础自测预习填空在同一平面内，两条直线有相交和平行两种位置关系．
　请举出生活中两条直线相交的例子：
______________________________.如相互贯穿的街道等课前 · 预学区自主学习　基础落实 本课目标温故知新基础自测预习填空 如果两条直线只有一个公共点，就说这两条直线______，
该公共点叫做这两条直线的______．
2. 对顶角的________相同，角的两边互为___________．
3. 对顶角的性质：对顶角________．
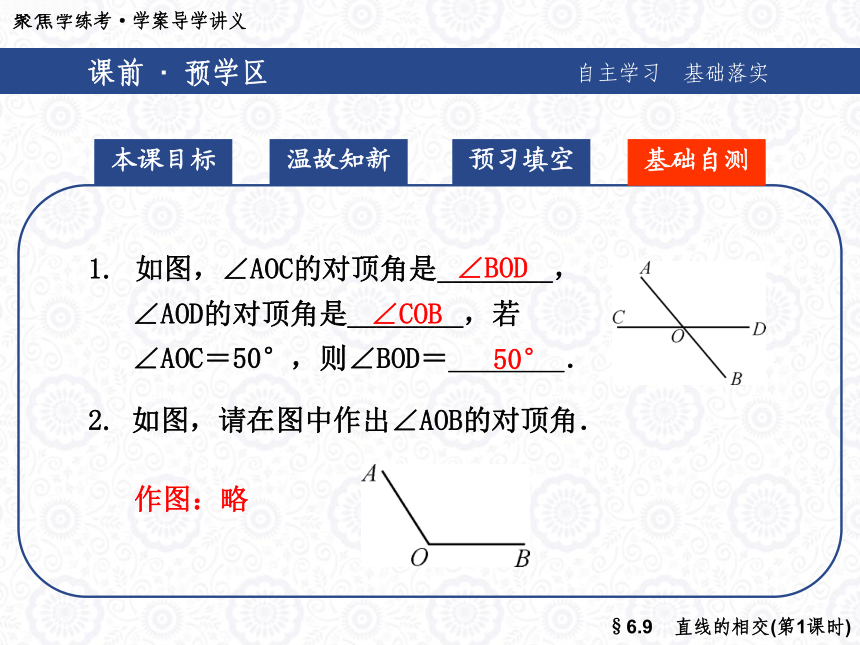
4. 两条直线相交于一点，共有________对对顶角．2相交交点度数反向延长线相等课前 · 预学区自主学习　基础落实 本课目标温故知新基础自测预习填空 如图，∠AOC的对顶角是________，
∠AOD的对顶角是________，若
∠AOC＝50°，则∠BOD＝________．
2. 如图，请在图中作出∠AOB的对顶角．作图：略 ∠BOD∠COB50°课前 · 预学区自主学习　基础落实 本课目标温故知新基础自测预习填空3. 下列说法中：①对顶角相等；②相等的角是对顶角；
③不是对顶角的两个角不相等；④不相等的两个角必
定不是对顶角．其中正确的说法是_______．(填序号)
4. 如图，直线AD与BE相交于点O，∠DOE与
∠COE互余，∠COE＝60°，则∠AOB的度
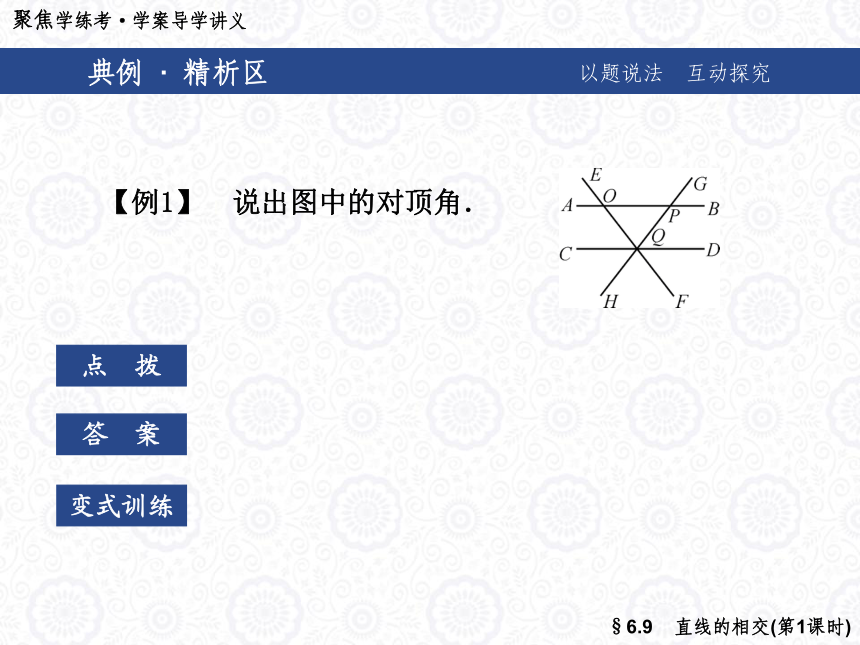
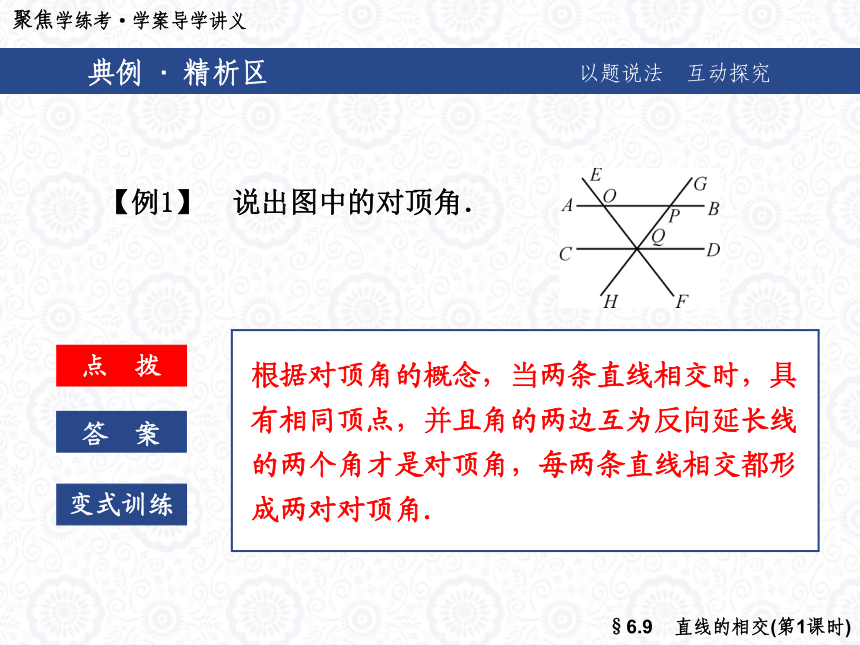
数为________．30° ①④典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例1】　说出图中的对顶角．典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例1】　说出图中的对顶角．根据对顶角的概念，当两条直线相交时，具
有相同顶点，并且角的两边互为反向延长线
的两个角才是对顶角，每两条直线相交都形
成两对对顶角．典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例1】　说出图中的对顶角．解：①以O为顶点：∠AOE与∠BOF，∠EOB与
∠AOF；
②以P为顶点：∠GPB与∠APH，∠APG与
∠QPH；
③以Q为顶点：∠CQH与∠GQD，∠CQF与
∠EQD，∠HQF与∠EQG，∠HQD与∠CQG，
∠FQD与∠CQE，∠FQG与∠HQE.典例 · 精析区以题说法　互动探究变式训练1　如图a，2条直线相交共有2对对顶角；如图b，
3条直线相交于一点，共有6对对顶角；如图c，4条线
相交于一点，共有________对对顶角；请寻找出对顶
角的对数与直线之间关系的规律，则n条直线相交于一
点时，共有________对对顶角．　　n(n－1) 12典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例2】　如图，直线AB和CD相交于点E，∠CEF＝56°，
∠BEF＝∠AEC＋40°，求∠AEC、∠BEF的度数．典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例2】　如图，直线AB和CD相交于点E，∠CEF＝56°，
∠BEF＝∠AEC＋40°，求∠AEC、∠BEF的度数．本题从∠BEF＝∠AEC＋40°入手，可设∠AEC
为x，则∠BEF表示为x＋40，再结合∠CEF与
平角∠AEB可列出方程求解．典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例2】　如图，直线AB和CD相交于点E，∠CEF＝56°，
∠BEF＝∠AEC＋40°，求∠AEC、∠BEF的度数．解：设∠AEC＝x，
则∠BEF＝x＋40，
得：x＋(x＋40)＋56＝180，
解得：x＝42，
∴42＋40＝82°.
答：∠AEC是42°，∠BEF是80°.典例 · 精析区以题说法　互动探究变式训练2　如图，直线AB与CD相交于O点，OE平分∠AOC，
OF平分∠DOB，说明：E、O、F三点在一条直线上．解：∵∠AOC＝∠BOD，
OE平分∠AOC，OF平分∠DOB，
∴∠AOE＝∠BOF，
∵∠AOE＋∠EOB＝180°，
∴∠BOF＋∠EOB＝180°，即∠EOF＝180°，
∴E、O、F三点在一条直线上．归纳总结 判断两个角是否是对顶角，关键在于看这两个角是
否是由两条直线相交所得到的，还要看这两个角是
否有公共顶点，角的两边是否互为反向延长线．
2. 对顶角一定相等，但相等的角未必是对顶角．对顶
角不仅反映了两个角的数量关系，而且也反映了两
个角之间的位置关系．
3. 已知条件中若有互余、互补、角平分线等时，应充
分利用这些已知条件的性质解题．在求角的度数时，
如有需要，可设其中一个角为x度，从而利用列方程
解决．随堂 · 检测区即时演练　查漏补缺 A. 基础部分（共8题，每题10分） (一)选择题
1. 下列图形中，∠1与∠2是对顶角的是 (　　)C随堂 · 检测区即时演练　查漏补缺 2. 如图，直线AB、CD交于点O，OE、OF是过O点的两条射线，
其中构成对顶角的是 (　　)
A. ∠AOF与∠DOE B. ∠EOF与∠BOE
C. ∠BOC与∠AOD D. ∠COF与∠BODC随堂 · 检测区即时演练　查漏补缺 3. 如图，两条直线AB、CD相交于点O，若∠2比∠1大60°，
则∠3的度数为 (　　)
A. 30° B. 60°
C. 120° D. 150°B随堂 · 检测区即时演练　查漏补缺 4. 如图，直线AB、CD相交于点O，射线OE平分∠BOC，已知
∠COE＝55°，则∠AOD的度数为 (　　)
A. 55° B. 125°
C. 110° D. 120°C随堂 · 检测区即时演练　查漏补缺 (二)填空题
5. 图中对顶角有________对．
6. 我们知道，三角形的三个内角的和等于180°，如图，
CE与AD相交于B点，∠C＝90°，∠A＝30°，∠D＝
70°，则∠E＝________．50°　 6随堂 · 检测区即时演练　查漏补缺 7. 如图，射线OB是射线OA的反向延长线，则OB的方向
是____________________． 在O点的南偏东60° 随堂 · 检测区即时演练　查漏补缺 (三)解答题
8. 如图，点O在直线AB上，且∠AOC＝∠BOD，则∠BOD
与∠BOC为互补角，请说明理由．略 随堂 · 检测区即时演练　查漏补缺 B. 提高部分（共2题，每题10分） 9. 如图，直线AB、CD相交于点O，OE平分∠BOD，∠AOD
＝2∠AOC，求∠BOE和∠COE的度数．解：设∠AOC＝x，则∠AOD＝2x，
得：x＋2x＝180°，解得：x＝60°，
∴∠AOC＝60°，∠AOD＝120°，
∵OE平分∠BOD，∠COE＝180°－∠DOE＝180°－30°＝150°.　随堂 · 检测区即时演练　查漏补缺 10. 已知直线AB、CD、EF相交于点O，∠1∶∠3＝3∶1，
∠2＝20°.
(1)图中的对顶角有哪几对？
(2)求∠DOE的度数． 解：(1)图中对顶角有：∠AOE与∠BOF，∠AOC与∠BOD，
∠EOC与∠DOF，∠EOB与∠AOF，∠COB与∠AOD，
∠COF与∠EOD，共6对对顶角．　
(2)设∠3＝x，则∠1＝3x，
得3x＋x＋20＝180，x＝40，即∠3＝40°，
∴∠DOE＝180°－∠3＝180°－40°＝140°.随堂 · 检测区即时演练　查漏补缺 C. 头脑风暴（选做题，20分） 11. 平面上有9条直线，无任何3条交于一点，试问这9条
直线的位置关系如何，才使它们的交点恰是26个？解：