6.4线段的和差

课件27张PPT。第六章 图形的初步知识§6.4 线段的和差课前 · 预学区本课目标预习填空基础自测温故知新自主学习　基础落实 1. 理解两条线段和与差的意义．
2. 会用直尺和圆规作线段的和与差．
3. 了解线段的中点的含义．
4. 会运用线段的和、差、倍、分等数量关系解决简单
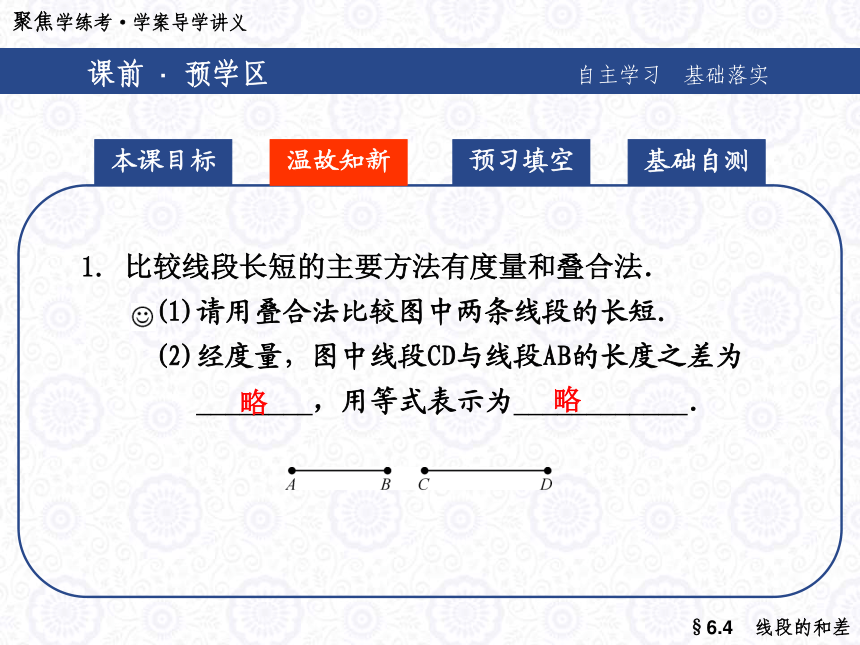
的线段长度问题．课前 · 预学区自主学习　基础落实 本课目标预习填空温故知新基础自测1. 比较线段长短的主要方法有度量和叠合法．
(1)请用叠合法比较图中两条线段的长短．
(2)经度量，图中线段CD与线段AB的长度之差为
________，用等式表示为____________．略略课前 · 预学区自主学习　基础落实 本课目标预习填空温故知新基础自测2. 连接两点线段的长度叫做这两点间的距离．
如图：AB＝4cm，AC＝2.5cm，则B、C间的距离为
________，用算式表示为BC＝________．　AB－AC1.5cm课前 · 预学区自主学习　基础落实 本课目标预习填空温故知新基础自测 一般地，如果一条线段的_______是另两条线段的
_______的和(差)，那么这条线段就叫做另两条线
段的和(差)．
2. 若一个点把一条线段分成相等的两条线段，则这个
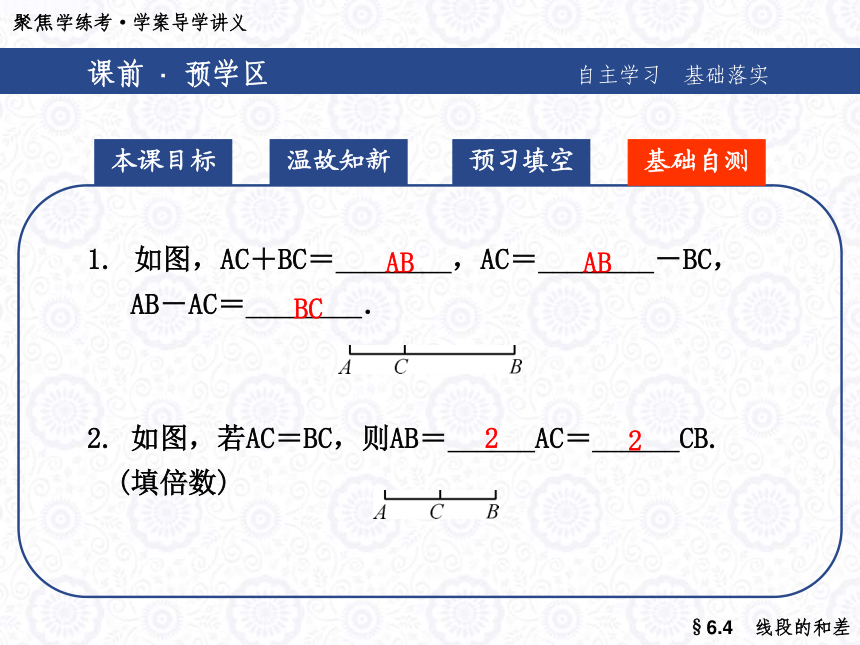
点叫做这条线段的________．中点长度长度课前 · 预学区自主学习　基础落实 本课目标预习填空温故知新基础自测 如图，AC＋BC＝________，AC＝________－BC，
AB－AC＝________．
2. 如图，若AC＝BC，则AB＝______AC＝______CB.
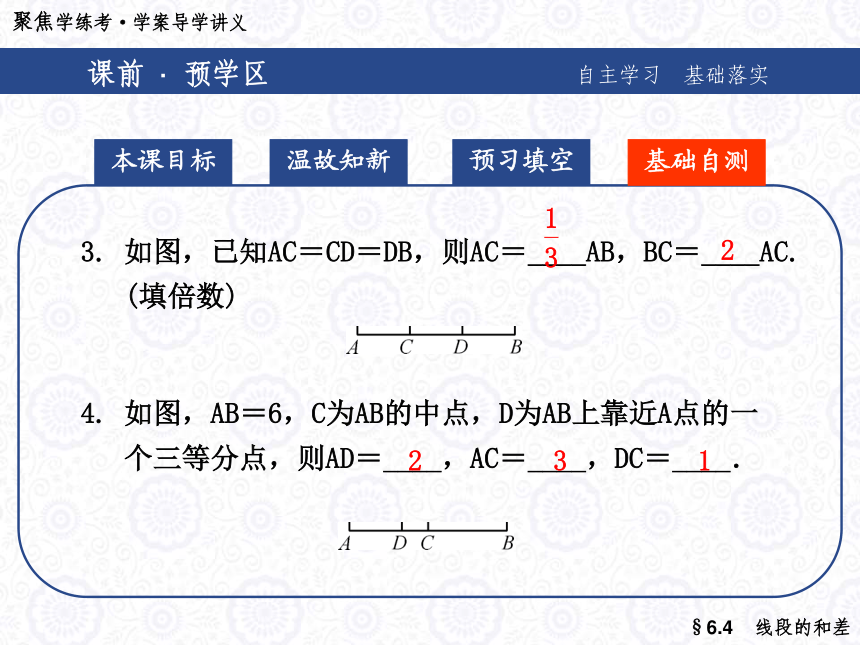
(填倍数)ABABBC22课前 · 预学区自主学习　基础落实 本课目标预习填空温故知新基础自测3. 如图，已知AC＝CD＝DB，则AC＝____AB，BC＝____AC.
(填倍数)
4. 如图，AB＝6，C为AB的中点，D为AB上靠近A点的一
个三等分点，则AD＝____，AC＝____，DC＝____．2231典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例1】　如图，已知线段BC＝2，反向延长BC至A，使AB
＝2BC，若M为AC的中点，求AM和MB的长度．典例 · 精析区以题说法　互动探究点 拨答 案【例1】　如图，已知线段BC＝2，反向延长BC至A，使AB
＝2BC，若M为AC的中点，求AM和MB的长度．抓住M为AC中点这个条件，先求AC，再求AM，
而MB可看成AB－AM或MC－BC，也可看成AC－
AM－BC.变式训练典例 · 精析区以题说法　互动探究点 拨答 案【例1】　如图，已知线段BC＝2，反向延长BC至A，使AB
＝2BC，若M为AC的中点，求AM和MB的长度．解：∵BC＝2，AB＝2BC，
∴AB＝2×2＝4，
∴AC＝BC＋AB＝2＋4＝6，
∵M为AC中点，
∴AM＝MC＝6÷2＝3，
∴MB＝MC－BC＝3－2＝1.变式训练典例 · 精析区以题说法　互动探究【例1】　如图，已知线段BC＝2，反向延长BC至A，使AB
＝2BC，若M为AC的中点，求AM和MB的长度．上题图中，若把条件“BC＝2”改为“MB＝
1”，其余条件不变，请求线段AC的长度．点 拨答 案变式训练典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例2】　如图，点C在线段AB上，AC＝6cm，BC＝8cm，点M、N
分别是AC、BC的中点．
(1)求线段MN的长；
(2)若AB＝14cm，C为线段AB上任一点，其余条件不变，求线
段MN的长．典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例2】　如图，点C在线段AB上，AC＝6cm，BC＝8cm，点M、N
分别是AC、BC的中点．
(1)求线段MN的长；
(2)若AB＝14cm，C为线段AB上任一点，其余条件不变，求线
段MN的长．第(1)题利用中点的意义易求，
第(2)题可先设AC＝xcm，再把BC的长用含
x的代数式表示，再结合中点的性质，求出
MN的长．典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例2】　如图，点C在线段AB上，AC＝6cm，BC＝8cm，点M、N
分别是AC、BC的中点．
(1)求线段MN的长；
(2)若AB＝14cm，C为线段AB上任一点，其余条件不变，求线
段MN的长．解：(1)∵AC＝6，BC＝8，M、N分别是AC、BC中点，∴MN＝MC＋CN＝3＋4＝7(cm)．典例 · 精析区以题说法　互动探究点 拨答 案变式训练【例2】　如图，点C在线段AB上，AC＝6cm，BC＝8cm，点M、N
分别是AC、BC的中点．
(1)求线段MN的长；
(2)若AB＝14cm，C为线段AB上任一点，其余条件不变，求线
段MN的长．(2)设AC＝xcm，则CB＝(14－x)cm，
∵M、N分别是AC、BC中点，典例 · 精析区以题说法　互动探究变式训练2　小明将一根长为20cm的木棒与一根长为10cm的
木棒捆绑，捆绑后全长为23cm，求这两根木棒捆绑部分
的长度．解：20＋10－23＝7cm.
答：两根木棒捆绑部分的长度是7cm.归纳总结 线段的和差实质是线段长度的和差，因此线段间
的数量关系就是长度上的数量关系．
2. 彻底理解中点的意义和寻找线段间的和差倍分关
系是解决线段计算类问题的关键．
3. 巧用代数设元是解决几何问题的一种重要思想．
4. 当点之间的相对位置不明确时，应进行分类讨论．随堂 · 检测区即时演练　查漏补缺 A. 基础部分（共8题，每题10分） (一)选择题
点P是线段AB上的点，下列不能说明点P是AB中点
的是 (　　)
A. AP＋BP＝AB B. AP＝BP
C. AP＝ AB D. AB＝2BPA随堂 · 检测区即时演练　查漏补缺 2. 如图，以下数量关系正确的是 (　　)
A. AC＋BC＝AD＋DB
B. AB－AC＝DB
C. AC＋CD－BD＝BC
D. AC＋BC－CD＝ACA随堂 · 检测区即时演练　查漏补缺 3. 数轴上有三点A、B、C，A点表示的数为－2，C点表示
的数为4，B点到A、C两点的距离相等，则B点表示的
数是 (　　)
A. 3 B. 1 C. －1 D. －3
4. 在射线OM上，从端点O顺次截取OA＝2，AB＝2OA，则线
段OB的长是 (　　)
A. 3 B. 4 C. 6 D. 2BC随堂 · 检测区即时演练　查漏补缺 5. 如图，C为线段AB的中点，AC＝1，则BC＝_____，
AB＝_____．
6. 如图，C为线段AB上一点，AB＝10，AC∶CB＝2∶3，
D为线段AB中点，则线段CD的长为______．121随堂 · 检测区即时演练　查漏补缺 (三)解答题
7. 如图，用尺规作图．
(1)画线段MN, 使MN＝AB＋AC；
(2)画线段PQ，使PQ＝DB－AB；
(3)比较线段MN、PQ、BC的大小，用“＞”把它们
连接起来．作图：略随堂 · 检测区即时演练　查漏补缺 8. 已知AB＝4cm，P为直线AB上一点，且PA＝3cm，
求PB的长．解：PB＝1或7　 随堂 · 检测区即时演练　查漏补缺 B. 提高部分（共2题，每题10分） 9. 如图，已知线段AB的长为a，延长线段AB至点C，
使BC＝ AB.
(1)求线段AC的长；
(2)若D为AC的中点，且DB＝1，求a的值．随堂 · 检测区即时演练　查漏补缺 10. 已知线段AC和BC在一条直线上，若AC＝8，BC＝3，
求线段AC和BC的中点间的距离．解：根据AC与BC在同一直线上，可知，有两种情形：
情形一：如图： 情形二：如图： 随堂 · 检测区即时演练　查漏补缺 C. 头脑风暴（选做题，20分） 11. 位于某大道AB上有四个居民小区A、B、C、D，其中AC＝CD
＝DB，现想要在AB段上建一家超市，要求各居民小区到超
市的路程之和最小，请你确定超市的位置，并说明理由．解：①若超市位于AC段上，如图：
则超市到四个居民区的路程之和＝PA＋PC＋PD＋PB
＝(PA＋PB)＋(PC＋PD)＝AB＋PC＋PC＋CD
＝AB＋CD＋2PC.
②若超市位于DB段上，如图：
则该路程之和＝AB＋CD＋2PD.随堂 · 检测区即时演练　查漏补缺 C. 头脑风暴（选做题，20分） 11. 位于某大道AB上有四个居民小区A、B、C、D，其中AC＝CD
＝DB，现想要在AB段上建一家超市，要求各居民小区到超
市的路程之和最小，请你确定超市的位置，并说明理由．③若超市位于CD段上，如图：
则该路程之和＝PA＋PB＋PC＋PD＝AB＋CD.
综上所述，显然当超市位于CD段上时，四个居民区到超市
的路程之和最小．