浙教版九年级上册 第4章《相似三角形》章末达标测试题(含解析)
文档属性
| 名称 | 浙教版九年级上册 第4章《相似三角形》章末达标测试题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 769.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版九年级上册 第4章《相似三角形》章末达标测试题
满分100分
一.选择题(共10小题,满分30分,每小题3分)
1.下列各组线段的长度成比例的是( )
A.1,2,3,4 B.2,3,4,6 C.3,4,5,6 D.5,10,15,20
2.已知矩形的长与宽分别为4和3,下列矩形与它相似的是( )
A. B.
C. D.
3.两个相似三角形的相似比是4:9,则其面积之比是( )
A.2:3 B.4:9 C.9:4 D.16:81
4.已知=,则的值为( )
A. B. C. D.
5.已知△ABC∽△DEF,且∠A=30°,∠E=30°,则∠C的度数是( )
A.120° B.60° C.90° D.30°
6.如图:AB∥CD∥EF,AD:DF=3:1,BE=12,那么CE的长为( )
A.3 B.4 C.5 D.6
7.如图,若点P为△ABC的边AB上一点(AB>AC),下列条件不能判定△ABC∽△ACP的是( )
A.∠B=∠ACP B.∠ACB=∠APC C. D.
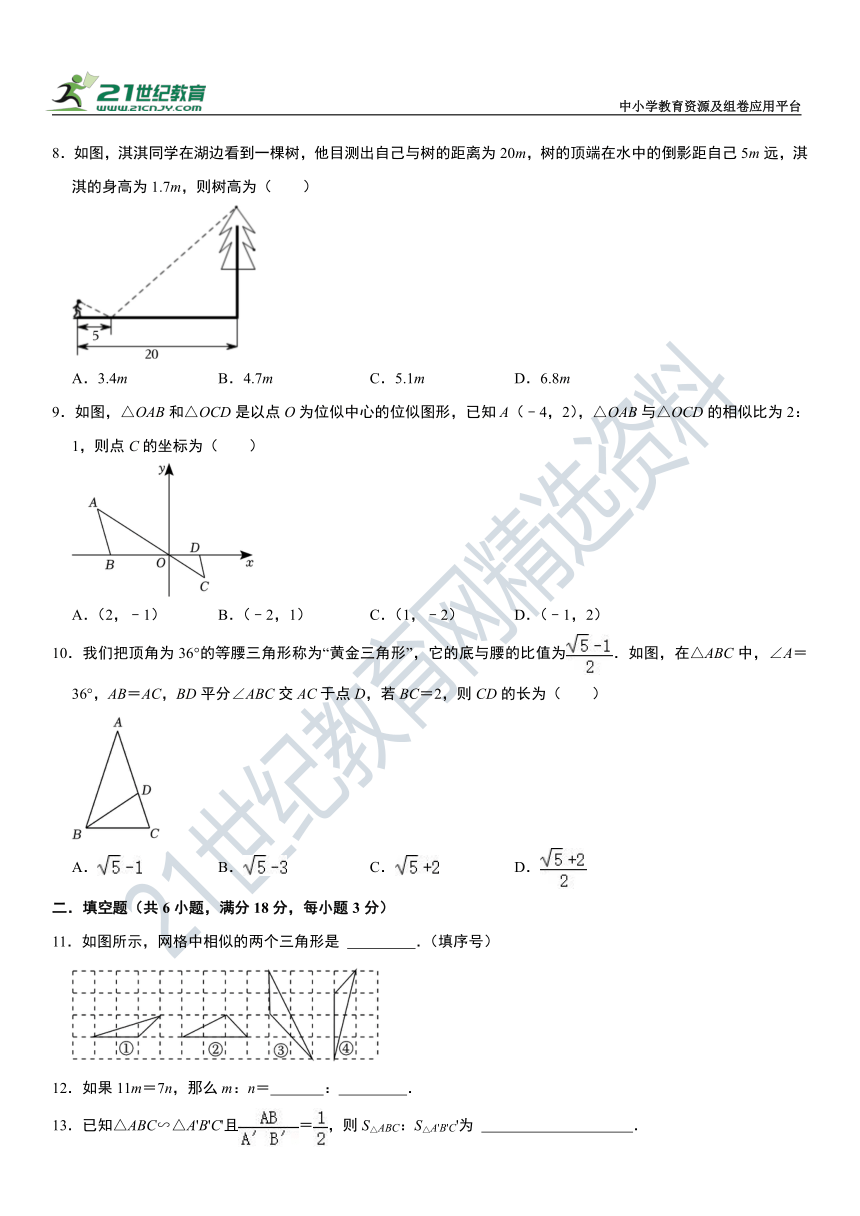
8.如图,淇淇同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,淇淇的身高为1.7m,则树高为( )
A.3.4m B.4.7m C.5.1m D.6.8m
9.如图,△OAB和△OCD是以点O为位似中心的位似图形,已知A(﹣4,2),△OAB与△OCD的相似比为2:1,则点C的坐标为( )
A.(2,﹣1) B.(﹣2,1) C.(1,﹣2) D.(﹣1,2)
10.我们把顶角为36°的等腰三角形称为“黄金三角形”,它的底与腰的比值为.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,若BC=2,则CD的长为( )
A. B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.如图所示,网格中相似的两个三角形是 .(填序号)
12.如果11m=7n,那么m:n= : .
13.已知△ABC∽△A'B'C'且=,则S△ABC:S△A'B'C'为 .
14.如图,在钝角△ABC中,AB=6cm,AC=12cm,点D从A点出发沿AB以1cm/s的速度向B点移动,点E从C点出发沿CA以2cm/s的速度向A点移动,如果两点同时移动,经过 秒时,△ADE与△ABC相似.
15.如图,已知在Rt△ABC中,∠ABC=90°,BD=CD,E是边AC上的一点,AD与BE交于点F,若∠DAB+∠CDE=90°,则= .
16.如图,在平面直角坐标系中,点A的坐标为(2,1),点B的坐标为(1,2),以点O为位似中心,在点O的异侧作△OAB的位似图形△OA1B1,使△OAB与△OA1B1的相似比为1:2;再以点O为位似中心,在点O的异侧作△OA1B1的位似图形△OA2B2,使△OA1B1与△OA2B2的相似比为1:2 以此类推,则点B2023的坐标为 .
三.解答题(共8小题,满分52分)
17.(5分)已知线段a,b满足=,且a+b=34.
(1)求a,b的值.
(2)若线段x是线段a,b的比例中项,求x的值.
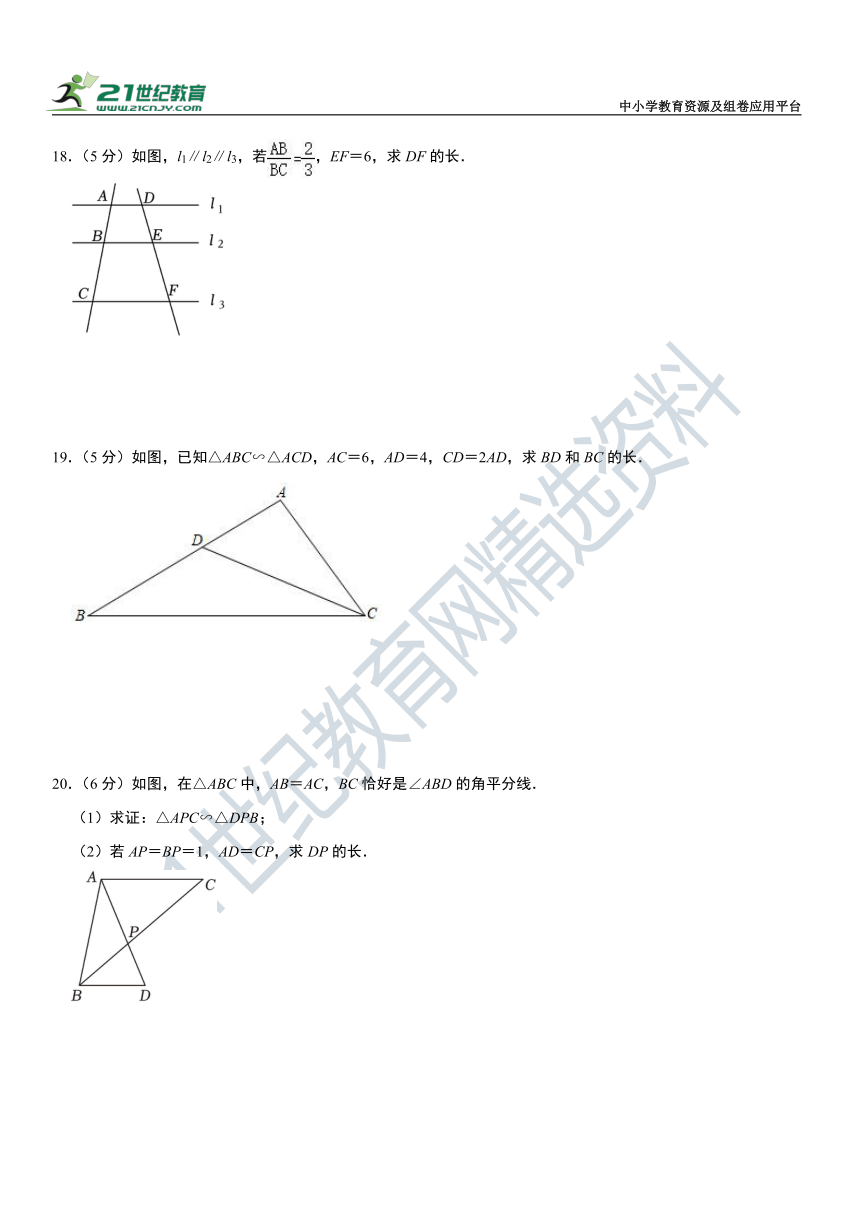
18.(5分)如图,l1∥l2∥l3,若,EF=6,求DF的长.
19.(5分)如图,已知△ABC∽△ACD,AC=6,AD=4,CD=2AD,求BD和BC的长.
20.(6分)如图,在△ABC中,AB=AC,BC恰好是∠ABD的角平分线.
(1)求证:△APC∽△DPB;
(2)若AP=BP=1,AD=CP,求DP的长.
21.(6分)如图,小明欲测量一座信号发射塔的高度.他站在该塔的影子上前后移动,直到他自己影子的顶端正好与塔的影子的顶端重合,此时他距离该塔20米.已知小明的身高是1.8米,他的影长是2米.
(1)图中△ABC与△ADE是否相似?为什么?
(2)求信号发射塔的高度.
22.(8分)在如图的方格纸中,△OAB的顶点坐标分别为O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P及点B的对应点B1的坐标;
(2)以原点O为位似中心,在位似中心的同侧画出△OAB的一个位似△OA2B2,使它与△OAB的位似比为2:1,并写出点B的对应点B2的坐标;
(3)△OAB的内部一点M的坐标为(a,b),写出M在△OA2B2中的对应点M2的坐标.
23.(8分)如图,在平面直角坐标系中,已知OA=6cm,OB=8cm.点P从点B开始沿BA边向终点A以1cm/s的速度移动;点Q从点A开始沿AO边向终点O以1cm/s的速度移动.有一点到达终点,另一点也停止运动.若P,Q同时出发,运动时间为t(s).
(1)用含t的代数式分别表示线段AQ和AP的长;
(2)当t为何值时,△APQ与△AOB相似?
24.(9分)阅读下面材料:
小波遇到这样一个问题:如图1,在△ABC中,BE是AC边上的中线,点D在BC边上,AD与BE相交于点P.
(1)小波发现,,过点C作CF∥AD,交BE的延长线于点F,通过构造△CEF(如图2),经过推理和计算得到的值为 .
(2)参考小波思考问题的方法,解决问题:
①如图3,在△ABC中,点D在BC的延长线上,,点E在AC上,且,求的值;
②如图4,在△ABC中,点D在BC的延长线上,,点E在AC上,且,求出的值.
浙教版九年级上册 第4章《相似三角形》章末达标测试题
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:A、∵1×4≠2×3,故此选项不符合题意;
B、∵2×6=3×4,故此选项符合题意;
C、∵3×6≠4×5,故此选项不符合题意;
D、∵5×20≠10×15,故此选项不符合题意.
故选:B.
2.【解答】解:A、因为3:4≠4:5,故A不符合题意;
B、因为3:4≠4:8,故B不符合题意;
C、因为3:6=4:8,故C符合题意;
D、因为3:6≠4:9,故D不符合题意.
故选:C.
3.【解答】解:∵两个相似三角形的相似比是4:9,
∴其面积之比是16:81,
故选:D.
4.【解答】解:设m=2k,n=3k,
则
=
=
=,
故选:B.
5.【解答】解:∵△ABC∽△DEF,∠E=30°,
∴∠ABC=∠E=30°,
∵∠A=30°,
∴∠C=180°﹣∠A﹣∠ABC=120°.
故选:A.
6.【解答】解:∵AB∥CD∥EF,
∴==3,
∴BC=3CE,
∴CE=BE=×12=3,
故选:A.
7.【解答】解:A、∠B=∠ACP,因为∠A=∠A,所以△ABC∽△ACP,不符合题意;
B、∠ACB=∠APC,因为∠A=∠A,所以△ABC∽△ACP,不符合题意;
C、,因为∠A=∠A,所以△ABC∽△ACP,不符合题意;
D、,因为∠A=∠A,而PC和BC的夹角为∠C,所以不能判定△ABC∽△ACP,符合题意.
故选:D.
8.【解答】解:由相似三角形的性质,设树高x米,
则=,
∴x=5.1m.
故选:C.
9.【解答】解:∵△OAB与△OCD的相似比为2:1,
∴OA:OC=2:1,
过点A作AE⊥x轴于点E,过点C作CF⊥x轴于点F.
∵A(﹣4,2),
∴AE=2,OE=4,
∵AE∥CF,
∴△AOE∽△COF,
∴==,
∴==2,
CF=1,OF=2,
∴C(2,﹣1),
故选:A.
10.【解答】解:∵∠A=36°,AB=AC,
∴∠ABC=∠C=(180°﹣∠A)=72°,
∵BD平分∠ABC,
∴∠DBC=∠ABC=36°,
∴∠BDC=180°﹣∠DBC﹣∠C=72°,
∴∠C=∠BDC=72°,
∴BC=BD,
∴△BDC是“黄金三角形”,
∴=,
∵BC=2,
∴DC=﹣1,
故选:A.
二.填空题(共6小题,满分18分,每小题3分)
11.【解答】解:图形①的三边为:2,,;
图形②的三边为:3,,;
图形③的三边为:2,2,2;
图形④的三边为:3,,,
∵,,
∴①与③相似,
故答案为:①③.
12.【解答】解:∵11m=7n,
∴m:n=7:11.
故答案为:7,11.
13.【解答】解:∵△ABC∽△A'B'C',=,
∴==.
故答案为:.
14.【解答】解:由题意可得,AD=tcm,AE=(12﹣2t)cm,
分两种情况:①若△ADE∽△ABC,则,
∴,
解得t=3;
②若△ADE∽△ACB,则,
∴,
∴t=.
综上所述,t=3或.
故答案为:3或.
15.【解答】解:如图,取AD的中点I,连接BI并延长,交AC于点J,
Rt△ABD中,BI=AI=DI,
∴∠IBA=∠IAB,∠IBD=∠IDB,
∵∠DAB+∠CDE=90°,∠IBA+∠IBD=90°,
∴∠IBD=∠CDE,
∴DE∥BJ,
∴=,=,
∵BD=CD,AI=DI,
∴CE=EJ,AJ=EJ,
∴ED=2JI,BJ=2DE=4JI,
∴BI=BJ﹣JI=4JI﹣JI=3JI,
∴==,
∵BI∥DE,
∴∠DEF=∠IBF,∠EDF=∠BIF,
∴△DEF∽△IBF,
∴==.
故答案为:.
16.【解答】解:根据题意,点B的坐标为(1,2),在点O的异侧作△OAB的位似图形△OA1B1,使△OAB与△OA1B1的相似比为1:2,
则B1(﹣2,﹣4),
再以点O为位似中心,在点O的异侧作△OA1B1的位似图形△OA2B2,使△OA1B1与△OA2B2的相似比为1:2,
则B2(4,8),
……
所以,点,
故点B2023的坐标为(﹣22023,﹣22024).
故答案为:(﹣22023,﹣22024).
三.解答题(共8小题,满分52分)
17.【解答】解:(1)∵=,
∴a:b=5:12,
∴设a=5k,b=12k,
∵a+b=34,
∴5k+12k=34,
∴k=2,
∴a=10,b=24;
(2)∵线段x是线段a,b的比例中项,
∴x2=ab=240,
∵x是线段,x>0,
∴x=4.
18.【解答】解:∵l1∥l2∥l3,
∴,
∵,
∴,
∵EF=6,
∴DE=4,
∵DF=DE+EF,DE=4,EF=6,
∴DF=10.
19.【解答】解:∵AD=4,CD=2AD,
∴CD=8,
∵△ABC∽△ACD,
∴==,即==,
解得,AB=9,BC=12,
∴BD=AB﹣AD=5.
20.【解答】(1)证明:∵AB=AC,
∴∠ABC=∠C,
∵BC是∠ABD的平分线,
∴∠ABC=∠DBC,
∴∠C=∠DBC,
又∠APC=∠DPB,
∴△APC∽△DPB.
(2)解:设DP=x,
∵AP=PB=1,
∴AD=AP+DP=1+x,
又AD=CP,
∴CP=1+x,
由(1)得:△APC∽△DPB,
∴AP:DP=PC:BP,
即:1:x=(x+1):1,
∴x2+x=1,
∴x2+x﹣1=0,
解得:,(不合题意,舍去).
∴.
21.【解答】解:(1)∵BC⊥AC,DE⊥AC,
∴DE∥BC,
∴△ABC∽△ADE,
(2)∵△ABC∽△ADE,
∴,
即,
∴DC=19.8(米),
∴古塔的高度为19.8米.
22.【解答】解:(1)位似中心P如图所示,P(﹣5,﹣1),B1(3,﹣5);
(2)△OA2B2如图所示,B2(﹣2,﹣6);
(3)点M2(2a,2b).
23.【解答】解:(1)∵OA=6cm,OB=8cm,
∴AB===10(cm),
∵点P的速度是每秒1个单位,点Q的速度是每秒1个单位,
∴AQ=tcm,AP=(10﹣t)cm;
(2)①∠APQ是直角时,△APQ∽△AOB,
∴=,
即,
解得t=>6,舍去;
②∠AQP是直角时,△AQP∽△AOB,
∴,
即,
解得t=,
综上所述,t=时,△APQ与△AOB相似.
24.【解答】解:(1)如图2,过点C作CF∥AD,交BE的延长线于点F,
∴∠F=∠APF,∠FCE=∠EAP,
∵BE为AC边的中线,
∴AE=CE,
∴△AEP≌△CEF(AAS),
∴AP=FC,
∵PD∥FC,
∴△BPD∽△BFC,
∴=,
∴=,
故答案为:;
(2)①如图3,过A作AF∥BC,交BP延长线于点F,
∴△AFE∽△CBE,
∴,
∵,
∴,
设AF=3x,BC=2x,
∵,
∴BD=x,
∵AF∥BD,
∴△AFP∽△DBP,
∴==;
②如图4,过C作CF∥AP交PB于F,
∴△BCF∽△BDP,
∴==,
设CF=3x,PD=4x,
∵CF∥AP,
∴△ECF∽△EAP,
∴,
∴AP=x,
∴==.
∴的值为.
浙教版九年级上册 第4章《相似三角形》章末达标测试题
满分100分
一.选择题(共10小题,满分30分,每小题3分)
1.下列各组线段的长度成比例的是( )
A.1,2,3,4 B.2,3,4,6 C.3,4,5,6 D.5,10,15,20
2.已知矩形的长与宽分别为4和3,下列矩形与它相似的是( )
A. B.
C. D.
3.两个相似三角形的相似比是4:9,则其面积之比是( )
A.2:3 B.4:9 C.9:4 D.16:81
4.已知=,则的值为( )
A. B. C. D.
5.已知△ABC∽△DEF,且∠A=30°,∠E=30°,则∠C的度数是( )
A.120° B.60° C.90° D.30°
6.如图:AB∥CD∥EF,AD:DF=3:1,BE=12,那么CE的长为( )
A.3 B.4 C.5 D.6
7.如图,若点P为△ABC的边AB上一点(AB>AC),下列条件不能判定△ABC∽△ACP的是( )
A.∠B=∠ACP B.∠ACB=∠APC C. D.
8.如图,淇淇同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,淇淇的身高为1.7m,则树高为( )
A.3.4m B.4.7m C.5.1m D.6.8m
9.如图,△OAB和△OCD是以点O为位似中心的位似图形,已知A(﹣4,2),△OAB与△OCD的相似比为2:1,则点C的坐标为( )
A.(2,﹣1) B.(﹣2,1) C.(1,﹣2) D.(﹣1,2)
10.我们把顶角为36°的等腰三角形称为“黄金三角形”,它的底与腰的比值为.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,若BC=2,则CD的长为( )
A. B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.如图所示,网格中相似的两个三角形是 .(填序号)
12.如果11m=7n,那么m:n= : .
13.已知△ABC∽△A'B'C'且=,则S△ABC:S△A'B'C'为 .
14.如图,在钝角△ABC中,AB=6cm,AC=12cm,点D从A点出发沿AB以1cm/s的速度向B点移动,点E从C点出发沿CA以2cm/s的速度向A点移动,如果两点同时移动,经过 秒时,△ADE与△ABC相似.
15.如图,已知在Rt△ABC中,∠ABC=90°,BD=CD,E是边AC上的一点,AD与BE交于点F,若∠DAB+∠CDE=90°,则= .
16.如图,在平面直角坐标系中,点A的坐标为(2,1),点B的坐标为(1,2),以点O为位似中心,在点O的异侧作△OAB的位似图形△OA1B1,使△OAB与△OA1B1的相似比为1:2;再以点O为位似中心,在点O的异侧作△OA1B1的位似图形△OA2B2,使△OA1B1与△OA2B2的相似比为1:2 以此类推,则点B2023的坐标为 .
三.解答题(共8小题,满分52分)
17.(5分)已知线段a,b满足=,且a+b=34.
(1)求a,b的值.
(2)若线段x是线段a,b的比例中项,求x的值.
18.(5分)如图,l1∥l2∥l3,若,EF=6,求DF的长.
19.(5分)如图,已知△ABC∽△ACD,AC=6,AD=4,CD=2AD,求BD和BC的长.
20.(6分)如图,在△ABC中,AB=AC,BC恰好是∠ABD的角平分线.
(1)求证:△APC∽△DPB;
(2)若AP=BP=1,AD=CP,求DP的长.
21.(6分)如图,小明欲测量一座信号发射塔的高度.他站在该塔的影子上前后移动,直到他自己影子的顶端正好与塔的影子的顶端重合,此时他距离该塔20米.已知小明的身高是1.8米,他的影长是2米.
(1)图中△ABC与△ADE是否相似?为什么?
(2)求信号发射塔的高度.
22.(8分)在如图的方格纸中,△OAB的顶点坐标分别为O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P及点B的对应点B1的坐标;
(2)以原点O为位似中心,在位似中心的同侧画出△OAB的一个位似△OA2B2,使它与△OAB的位似比为2:1,并写出点B的对应点B2的坐标;
(3)△OAB的内部一点M的坐标为(a,b),写出M在△OA2B2中的对应点M2的坐标.
23.(8分)如图,在平面直角坐标系中,已知OA=6cm,OB=8cm.点P从点B开始沿BA边向终点A以1cm/s的速度移动;点Q从点A开始沿AO边向终点O以1cm/s的速度移动.有一点到达终点,另一点也停止运动.若P,Q同时出发,运动时间为t(s).
(1)用含t的代数式分别表示线段AQ和AP的长;
(2)当t为何值时,△APQ与△AOB相似?
24.(9分)阅读下面材料:
小波遇到这样一个问题:如图1,在△ABC中,BE是AC边上的中线,点D在BC边上,AD与BE相交于点P.
(1)小波发现,,过点C作CF∥AD,交BE的延长线于点F,通过构造△CEF(如图2),经过推理和计算得到的值为 .
(2)参考小波思考问题的方法,解决问题:
①如图3,在△ABC中,点D在BC的延长线上,,点E在AC上,且,求的值;
②如图4,在△ABC中,点D在BC的延长线上,,点E在AC上,且,求出的值.
浙教版九年级上册 第4章《相似三角形》章末达标测试题
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:A、∵1×4≠2×3,故此选项不符合题意;
B、∵2×6=3×4,故此选项符合题意;
C、∵3×6≠4×5,故此选项不符合题意;
D、∵5×20≠10×15,故此选项不符合题意.
故选:B.
2.【解答】解:A、因为3:4≠4:5,故A不符合题意;
B、因为3:4≠4:8,故B不符合题意;
C、因为3:6=4:8,故C符合题意;
D、因为3:6≠4:9,故D不符合题意.
故选:C.
3.【解答】解:∵两个相似三角形的相似比是4:9,
∴其面积之比是16:81,
故选:D.
4.【解答】解:设m=2k,n=3k,
则
=
=
=,
故选:B.
5.【解答】解:∵△ABC∽△DEF,∠E=30°,
∴∠ABC=∠E=30°,
∵∠A=30°,
∴∠C=180°﹣∠A﹣∠ABC=120°.
故选:A.
6.【解答】解:∵AB∥CD∥EF,
∴==3,
∴BC=3CE,
∴CE=BE=×12=3,
故选:A.
7.【解答】解:A、∠B=∠ACP,因为∠A=∠A,所以△ABC∽△ACP,不符合题意;
B、∠ACB=∠APC,因为∠A=∠A,所以△ABC∽△ACP,不符合题意;
C、,因为∠A=∠A,所以△ABC∽△ACP,不符合题意;
D、,因为∠A=∠A,而PC和BC的夹角为∠C,所以不能判定△ABC∽△ACP,符合题意.
故选:D.
8.【解答】解:由相似三角形的性质,设树高x米,
则=,
∴x=5.1m.
故选:C.
9.【解答】解:∵△OAB与△OCD的相似比为2:1,
∴OA:OC=2:1,
过点A作AE⊥x轴于点E,过点C作CF⊥x轴于点F.
∵A(﹣4,2),
∴AE=2,OE=4,
∵AE∥CF,
∴△AOE∽△COF,
∴==,
∴==2,
CF=1,OF=2,
∴C(2,﹣1),
故选:A.
10.【解答】解:∵∠A=36°,AB=AC,
∴∠ABC=∠C=(180°﹣∠A)=72°,
∵BD平分∠ABC,
∴∠DBC=∠ABC=36°,
∴∠BDC=180°﹣∠DBC﹣∠C=72°,
∴∠C=∠BDC=72°,
∴BC=BD,
∴△BDC是“黄金三角形”,
∴=,
∵BC=2,
∴DC=﹣1,
故选:A.
二.填空题(共6小题,满分18分,每小题3分)
11.【解答】解:图形①的三边为:2,,;
图形②的三边为:3,,;
图形③的三边为:2,2,2;
图形④的三边为:3,,,
∵,,
∴①与③相似,
故答案为:①③.
12.【解答】解:∵11m=7n,
∴m:n=7:11.
故答案为:7,11.
13.【解答】解:∵△ABC∽△A'B'C',=,
∴==.
故答案为:.
14.【解答】解:由题意可得,AD=tcm,AE=(12﹣2t)cm,
分两种情况:①若△ADE∽△ABC,则,
∴,
解得t=3;
②若△ADE∽△ACB,则,
∴,
∴t=.
综上所述,t=3或.
故答案为:3或.
15.【解答】解:如图,取AD的中点I,连接BI并延长,交AC于点J,
Rt△ABD中,BI=AI=DI,
∴∠IBA=∠IAB,∠IBD=∠IDB,
∵∠DAB+∠CDE=90°,∠IBA+∠IBD=90°,
∴∠IBD=∠CDE,
∴DE∥BJ,
∴=,=,
∵BD=CD,AI=DI,
∴CE=EJ,AJ=EJ,
∴ED=2JI,BJ=2DE=4JI,
∴BI=BJ﹣JI=4JI﹣JI=3JI,
∴==,
∵BI∥DE,
∴∠DEF=∠IBF,∠EDF=∠BIF,
∴△DEF∽△IBF,
∴==.
故答案为:.
16.【解答】解:根据题意,点B的坐标为(1,2),在点O的异侧作△OAB的位似图形△OA1B1,使△OAB与△OA1B1的相似比为1:2,
则B1(﹣2,﹣4),
再以点O为位似中心,在点O的异侧作△OA1B1的位似图形△OA2B2,使△OA1B1与△OA2B2的相似比为1:2,
则B2(4,8),
……
所以,点,
故点B2023的坐标为(﹣22023,﹣22024).
故答案为:(﹣22023,﹣22024).
三.解答题(共8小题,满分52分)
17.【解答】解:(1)∵=,
∴a:b=5:12,
∴设a=5k,b=12k,
∵a+b=34,
∴5k+12k=34,
∴k=2,
∴a=10,b=24;
(2)∵线段x是线段a,b的比例中项,
∴x2=ab=240,
∵x是线段,x>0,
∴x=4.
18.【解答】解:∵l1∥l2∥l3,
∴,
∵,
∴,
∵EF=6,
∴DE=4,
∵DF=DE+EF,DE=4,EF=6,
∴DF=10.
19.【解答】解:∵AD=4,CD=2AD,
∴CD=8,
∵△ABC∽△ACD,
∴==,即==,
解得,AB=9,BC=12,
∴BD=AB﹣AD=5.
20.【解答】(1)证明:∵AB=AC,
∴∠ABC=∠C,
∵BC是∠ABD的平分线,
∴∠ABC=∠DBC,
∴∠C=∠DBC,
又∠APC=∠DPB,
∴△APC∽△DPB.
(2)解:设DP=x,
∵AP=PB=1,
∴AD=AP+DP=1+x,
又AD=CP,
∴CP=1+x,
由(1)得:△APC∽△DPB,
∴AP:DP=PC:BP,
即:1:x=(x+1):1,
∴x2+x=1,
∴x2+x﹣1=0,
解得:,(不合题意,舍去).
∴.
21.【解答】解:(1)∵BC⊥AC,DE⊥AC,
∴DE∥BC,
∴△ABC∽△ADE,
(2)∵△ABC∽△ADE,
∴,
即,
∴DC=19.8(米),
∴古塔的高度为19.8米.
22.【解答】解:(1)位似中心P如图所示,P(﹣5,﹣1),B1(3,﹣5);
(2)△OA2B2如图所示,B2(﹣2,﹣6);
(3)点M2(2a,2b).
23.【解答】解:(1)∵OA=6cm,OB=8cm,
∴AB===10(cm),
∵点P的速度是每秒1个单位,点Q的速度是每秒1个单位,
∴AQ=tcm,AP=(10﹣t)cm;
(2)①∠APQ是直角时,△APQ∽△AOB,
∴=,
即,
解得t=>6,舍去;
②∠AQP是直角时,△AQP∽△AOB,
∴,
即,
解得t=,
综上所述,t=时,△APQ与△AOB相似.
24.【解答】解:(1)如图2,过点C作CF∥AD,交BE的延长线于点F,
∴∠F=∠APF,∠FCE=∠EAP,
∵BE为AC边的中线,
∴AE=CE,
∴△AEP≌△CEF(AAS),
∴AP=FC,
∵PD∥FC,
∴△BPD∽△BFC,
∴=,
∴=,
故答案为:;
(2)①如图3,过A作AF∥BC,交BP延长线于点F,
∴△AFE∽△CBE,
∴,
∵,
∴,
设AF=3x,BC=2x,
∵,
∴BD=x,
∵AF∥BD,
∴△AFP∽△DBP,
∴==;
②如图4,过C作CF∥AP交PB于F,
∴△BCF∽△BDP,
∴==,
设CF=3x,PD=4x,
∵CF∥AP,
∴△ECF∽△EAP,
∴,
∴AP=x,
∴==.
∴的值为.
同课章节目录
