浙教版数学八年级上册 5.4一次函数的图象(第2课时)一次函数的性质课件 18张PPT
文档属性
| 名称 | 浙教版数学八年级上册 5.4一次函数的图象(第2课时)一次函数的性质课件 18张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 284.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-23 09:47:42 | ||
图片预览





文档简介
(共18张PPT)
第5章 一次函数
5.4 一次函数的图象
第2课时 一次函数的性质
学习目标
根据一次函数的图象和表达式探索并理解k>0和k<0时图象的变化,归纳出正比例函数中k对函数增减性的影响.
掌握一次函数的图象及性质,会利用一次函数的图象和性质解决简单的实际问题.
复习引入
1.一次函数图象有什么特点?
2.画一次函数图象需要描出几个点?
一次函数y=kx+b的图象是一条直线,直线上所有点的坐标都满足表达式y=kx+b.
y
x
O
1
2
3
1
2
3
4
-1
-2
-3
-1
-2
-3
-4
5
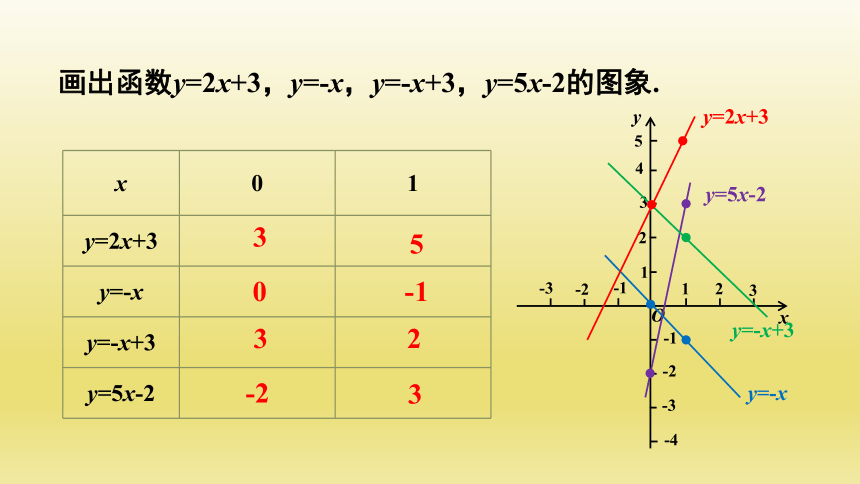
画出函数y=2x+3,y=-x,y=-x+3,y=5x-2的图象.
x 0 1
y=2x+3
y=-x
y=-x+3
y=5x-2
3
5
0
-1
3
2
-2
3
y=2x+3
y=-x
y=-x+3
y=5x-2
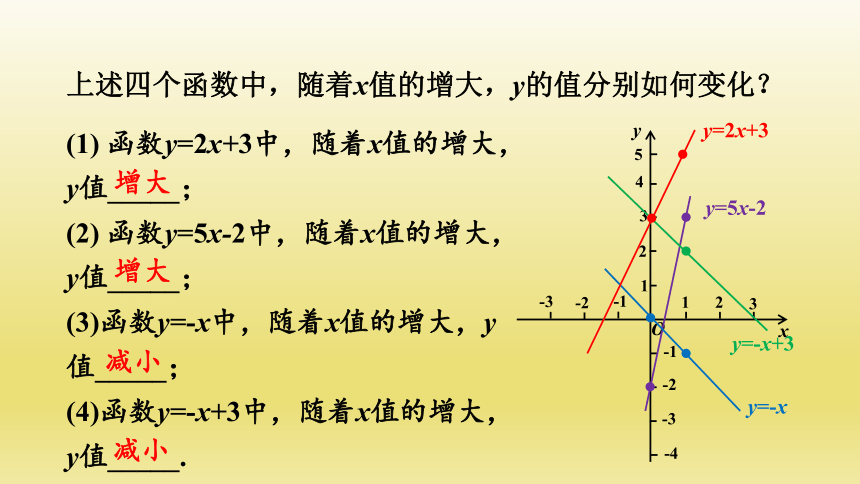
上述四个函数中,随着x值的增大,y的值分别如何变化?
(1) 函数y=2x+3中,随着x值的增大,y值_____;
(2) 函数y=5x-2中,随着x值的增大,y值_____;
(3)函数y=-x中,随着x值的增大,y值_____;
(4)函数y=-x+3中,随着x值的增大,y值_____.
增大
增大
减小
减小
y
x
O
1
2
3
1
2
3
4
-1
-2
-3
-1
-2
-3
-4
5
y=2x+3
y=-x
y=-x+3
y=5x-2
一次函数的增减性
在一次函数y=kx+b中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.
议一议
(1)哪些函数的图象与 y 轴的交点在 x 轴的上方,哪些函数与y轴的交点在x轴的下方?
(2)函数的图象与 y 轴的交点在 x 轴的上方和函数的图象与 y 轴的交点在 x 轴的下方,这两种函数,它们的区别与常数项有怎样的关系?
(3)正比例函数的图象一定经过哪个点?
参考前面所画出的函数图象,请谈谈:
一次函数y=kx+b的图象是经过y轴上的点(0,b)的一条直线.
当b>0时,点(0,b)在x轴的上方;
当b<0时,点(0,b)在x轴的下方;
当b=0 时,点(0,0)是原点,即正比例函数y=kx的图象是经过原点的一条直线.
归纳总结
合作探究
上述四个函数的图象分别经过哪些象限?
(1) 函数y=2x+3经过___________象限;
(2) 函数y=5x-2经过___________象限;
(3) 函数y=-x经过____________象限;
(4) 函数y=-x+3经过____________象限.
一、二、三
一、三、四
二、四
一、二、四
y
x
O
1
2
3
1
2
3
4
-1
-2
-3
-1
-2
-3
-4
5
y=2x+3
y=-x
y=-x+3
y=5x-2
k >0,b>0
k < 0,b < 0
k < 0,b = 0
k < 0,b > 0
k > 0,b < 0
k > 0,b = 0
练一练:根据一次函数的图象判断k,b的正负:
一次函数图象所过象限
在一次函数y=kx+b中(k,b都是常数,且k≠0),
当k>0, b>0时,函数图象经过一、二、三象限;
当k>0 ,b<0时,函数图象经过一、三、四象限;
当k<0 ,b>0时,函数图象经过一、二、四象限;
当k<0 ,b<0时,函数图象经过二、三、四象限.
当k>0 ,b=0时,函数图象经过一、三象限;
当k<0 ,b=0时,函数图象经过二、四象限;
典例精讲
例1 已知关于x的一次函数y=(2k-1)x+(2k+1).
(1) 当k满足什么条件时,函数y的值随x的值的增大而增大?
(2) 当k满足什么条件时,y=(2k-1)x+(2k+1)的图象经过原点?
解:(1) 当2k-1>0时,y的值随x的值增大而增大.
解2k-1>0,得k>0.5.
(2) 当2k+1=0,即k=-0.5时,
函数y=(2k-1)x+(2k+1)的图象经过原点.
典例精讲
例2 某面食加工部每周用10 000元流动资金采购面粉及其他物品,其中购买面粉的质量在1 500kg-2 000kg之间,面粉的单价为3.6元/千克,用剩余款额y元购买其他物品.设购买面粉的质量为x kg.
(1) 求y与x的函数关系式,并写出自变量的取值范围.
解: (1)由题意可知购买面粉的资金为3.6x元,总资金为10 000元,即3.6x+y=10 000,所以该函数关系式为:y=-3.6x +10 000,其中x的取值范围是1 500≤x≤2 000.
例2 某面食加工部每周用10 000元流动资金采购面粉及其他物品,其中购买面粉的质量在1 500kg-2 000kg之间,面粉的单价为3.6元/千克,用剩余款额y元购买其他物品.设购买面粉的质量为x kg.
(2)求出购买其他物品的款额 y 的取值范围.
(2)∵y=-3.6x+10 000,k=-3.6<0,∴y的值随x的值增大而减小.
∵1 500≤x≤2 000,∴y的值最大为-3.6×1 500+10 000=4 600;
最小为 -3.6×2 000+10 000=2 800.
故y的取值范围为2 800≤y≤4 600.
随堂练习
1. P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象上的两点,下列判断中,正确的是( )
A. y1>y2 B. y1<y2
C. 当x1<x2时,y1<y2 D. 当x1<x2时,y1>y2
D
解析:根据一次函数的性质:
当k<0时,y随x的增大而减小.
随堂练习
2. 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1) 函数值y 随x的增大而增大;
(2) 函数图象与y 轴的负半轴相交;
(3) 函数的图象过第二、三、四象限.
课堂小结
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
① b>0时,直线经过 一、二、四象限;
② b<0时,直线经过二、三、四象限.
① b>0时,直线经过一、二、三象限;
② b<0时,直线经过一、三、四象限.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
③ b=0时,直线经过一、三象限.
③ b=0时,直线经过二、四象限.
感谢观看!
第5章 一次函数
5.4 一次函数的图象
第2课时 一次函数的性质
学习目标
根据一次函数的图象和表达式探索并理解k>0和k<0时图象的变化,归纳出正比例函数中k对函数增减性的影响.
掌握一次函数的图象及性质,会利用一次函数的图象和性质解决简单的实际问题.
复习引入
1.一次函数图象有什么特点?
2.画一次函数图象需要描出几个点?
一次函数y=kx+b的图象是一条直线,直线上所有点的坐标都满足表达式y=kx+b.
y
x
O
1
2
3
1
2
3
4
-1
-2
-3
-1
-2
-3
-4
5
画出函数y=2x+3,y=-x,y=-x+3,y=5x-2的图象.
x 0 1
y=2x+3
y=-x
y=-x+3
y=5x-2
3
5
0
-1
3
2
-2
3
y=2x+3
y=-x
y=-x+3
y=5x-2
上述四个函数中,随着x值的增大,y的值分别如何变化?
(1) 函数y=2x+3中,随着x值的增大,y值_____;
(2) 函数y=5x-2中,随着x值的增大,y值_____;
(3)函数y=-x中,随着x值的增大,y值_____;
(4)函数y=-x+3中,随着x值的增大,y值_____.
增大
增大
减小
减小
y
x
O
1
2
3
1
2
3
4
-1
-2
-3
-1
-2
-3
-4
5
y=2x+3
y=-x
y=-x+3
y=5x-2
一次函数的增减性
在一次函数y=kx+b中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.
议一议
(1)哪些函数的图象与 y 轴的交点在 x 轴的上方,哪些函数与y轴的交点在x轴的下方?
(2)函数的图象与 y 轴的交点在 x 轴的上方和函数的图象与 y 轴的交点在 x 轴的下方,这两种函数,它们的区别与常数项有怎样的关系?
(3)正比例函数的图象一定经过哪个点?
参考前面所画出的函数图象,请谈谈:
一次函数y=kx+b的图象是经过y轴上的点(0,b)的一条直线.
当b>0时,点(0,b)在x轴的上方;
当b<0时,点(0,b)在x轴的下方;
当b=0 时,点(0,0)是原点,即正比例函数y=kx的图象是经过原点的一条直线.
归纳总结
合作探究
上述四个函数的图象分别经过哪些象限?
(1) 函数y=2x+3经过___________象限;
(2) 函数y=5x-2经过___________象限;
(3) 函数y=-x经过____________象限;
(4) 函数y=-x+3经过____________象限.
一、二、三
一、三、四
二、四
一、二、四
y
x
O
1
2
3
1
2
3
4
-1
-2
-3
-1
-2
-3
-4
5
y=2x+3
y=-x
y=-x+3
y=5x-2
k >0,b>0
k < 0,b < 0
k < 0,b = 0
k < 0,b > 0
k > 0,b < 0
k > 0,b = 0
练一练:根据一次函数的图象判断k,b的正负:
一次函数图象所过象限
在一次函数y=kx+b中(k,b都是常数,且k≠0),
当k>0, b>0时,函数图象经过一、二、三象限;
当k>0 ,b<0时,函数图象经过一、三、四象限;
当k<0 ,b>0时,函数图象经过一、二、四象限;
当k<0 ,b<0时,函数图象经过二、三、四象限.
当k>0 ,b=0时,函数图象经过一、三象限;
当k<0 ,b=0时,函数图象经过二、四象限;
典例精讲
例1 已知关于x的一次函数y=(2k-1)x+(2k+1).
(1) 当k满足什么条件时,函数y的值随x的值的增大而增大?
(2) 当k满足什么条件时,y=(2k-1)x+(2k+1)的图象经过原点?
解:(1) 当2k-1>0时,y的值随x的值增大而增大.
解2k-1>0,得k>0.5.
(2) 当2k+1=0,即k=-0.5时,
函数y=(2k-1)x+(2k+1)的图象经过原点.
典例精讲
例2 某面食加工部每周用10 000元流动资金采购面粉及其他物品,其中购买面粉的质量在1 500kg-2 000kg之间,面粉的单价为3.6元/千克,用剩余款额y元购买其他物品.设购买面粉的质量为x kg.
(1) 求y与x的函数关系式,并写出自变量的取值范围.
解: (1)由题意可知购买面粉的资金为3.6x元,总资金为10 000元,即3.6x+y=10 000,所以该函数关系式为:y=-3.6x +10 000,其中x的取值范围是1 500≤x≤2 000.
例2 某面食加工部每周用10 000元流动资金采购面粉及其他物品,其中购买面粉的质量在1 500kg-2 000kg之间,面粉的单价为3.6元/千克,用剩余款额y元购买其他物品.设购买面粉的质量为x kg.
(2)求出购买其他物品的款额 y 的取值范围.
(2)∵y=-3.6x+10 000,k=-3.6<0,∴y的值随x的值增大而减小.
∵1 500≤x≤2 000,∴y的值最大为-3.6×1 500+10 000=4 600;
最小为 -3.6×2 000+10 000=2 800.
故y的取值范围为2 800≤y≤4 600.
随堂练习
1. P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象上的两点,下列判断中,正确的是( )
A. y1>y2 B. y1<y2
C. 当x1<x2时,y1<y2 D. 当x1<x2时,y1>y2
D
解析:根据一次函数的性质:
当k<0时,y随x的增大而减小.
随堂练习
2. 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1) 函数值y 随x的增大而增大;
(2) 函数图象与y 轴的负半轴相交;
(3) 函数的图象过第二、三、四象限.
课堂小结
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
① b>0时,直线经过 一、二、四象限;
② b<0时,直线经过二、三、四象限.
① b>0时,直线经过一、二、三象限;
② b<0时,直线经过一、三、四象限.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
③ b=0时,直线经过一、三象限.
③ b=0时,直线经过二、四象限.
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
