1.5全等三角形地判定(第四课时)教案 2023-2024学年浙教版数学 八年级上册
文档属性
| 名称 | 1.5全等三角形地判定(第四课时)教案 2023-2024学年浙教版数学 八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 142.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-23 00:00:00 | ||
图片预览


文档简介
浙教版数学八年级上册1.5 全等三角形的判定(第四课时)教案
教材分析
全等三角形是几何图形部分的重要内容之一,帮助学生了解全等三角形判定是对简单的平面图形的进一步研究,也是后续研究多边形的性质,三角函数等知识的基础,在平面几何中有着非常重要的地位和作用。
学情分析
首先是学生的知识特征,八年级的学生已经学习了全等三角形的概念和性质。但是学生对数学语言的理解还有待提高,如何判定两个三角形全等,需要老师积极引导。
然后是学生的心理特征,八年级的学生好奇心重,求知欲强,教师通过合适的方法引入有助于他们更好地三角形的相关内容。
教学目标
知识与技能
1.掌握三角形全等的判定定理(AAS)
2.理解角平分线的性质。
过程与方法:在学习过程中培养自主探究能力和严谨的数学思维。
情感态度与价值观:能够体会数学严谨的推理,利用三角形全等解决现实问题,感受数学的乐趣
教学重难点
重点:本节教学的重点是两个三角形全等的条件:两角及其中一个角的对边对应相等的两个三角形全等
难点:例题中需要添加辅助线,证明的思路较复杂,是本节教学的难点
教学方法、手段
教学方法:讲授法、探究法
教学手段:板书与多媒体课件相结合
教学过程
回顾旧知:
到目前为止,我们已学过哪些方法判定两三角形全等?
1. 全等三角形的定义
能够完全重合的两个三角形全等
2.边边边公理(SSS)
三边对应相等的两个三角形全等
3.边角边公理(SAS)
两边及其夹角对应相等的两个三角形全等
4.角边角公理(ASA)
两个角和这两个角的夹边对应相等的两个三角形全等。
二、思考讨论
已知两个三角形中,有两个角和其中一个角的对边对应相等,那么两个三角形是否全等?
探究:在△ABC和△DEF中, ∠A=∠D, ∠B=∠E,BC=EF, △ABC和△DEF全等吗?为什么?
证明:∵ ∠A=∠D, ∠B=∠E(已知)
∴∠C=∠F(三角形内角和定理)
在△ABC和△DEF中
∠B=∠E
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
你能从上题中得到什么结论?
两角及一角的对边对应相等的两个三角形全等
三、讲授新课:
判定三角形全等的定理4:
两角及一角的对边对应相等的两个三角形全等 (简写成“角角边”或“AAS”)
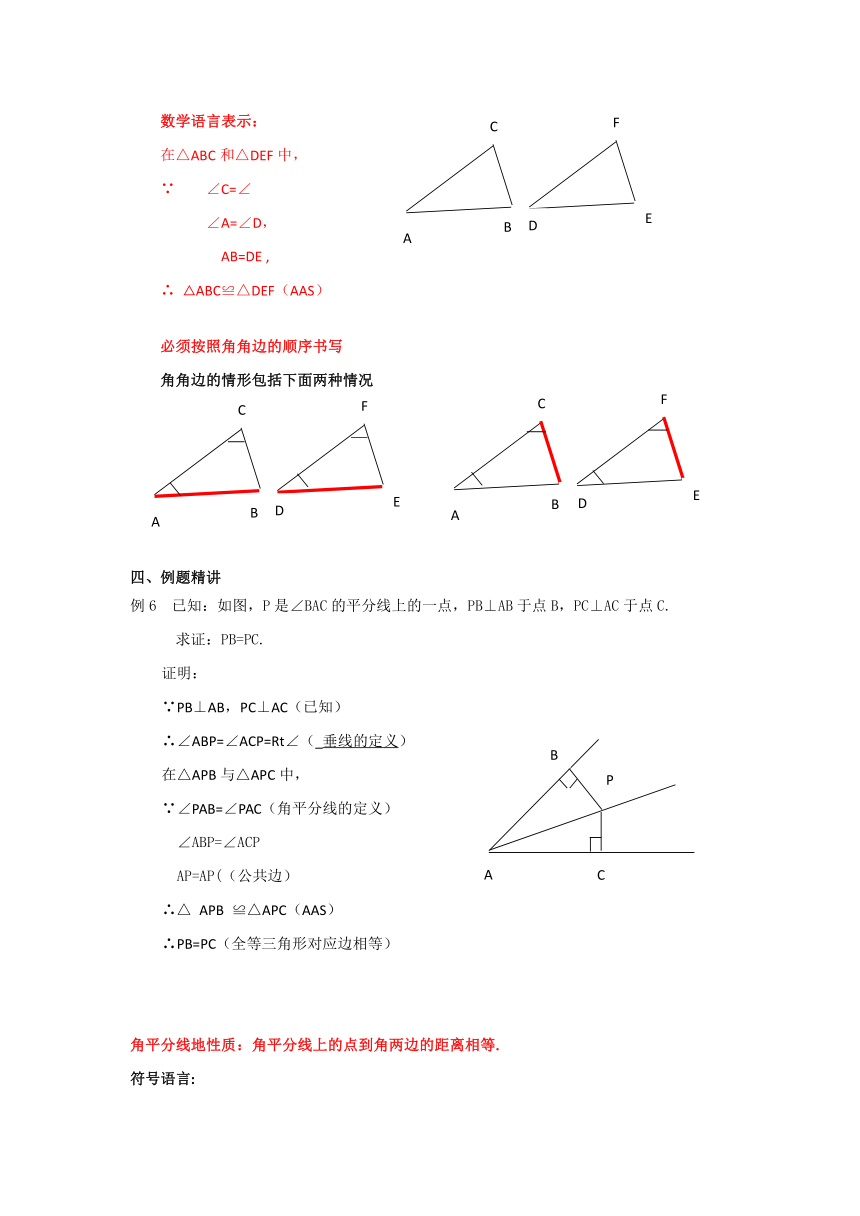
数学语言表示:
在△ABC和△DEF中,
∵ ∠C=∠
∠A=∠D,
AB=DE ,
∴ △ABC≌△DEF(AAS)
必须按照角角边的顺序书写
角角边的情形包括下面两种情况
例题精讲
例6 已知:如图,P是∠BAC的平分线上的一点,PB⊥AB于点B,PC⊥AC于点C.
求证:PB=PC.
证明:
∵PB⊥AB,PC⊥AC(已知)
∴∠ABP=∠ACP=Rt∠(_垂线的定义)
在△APB与△APC中,
∵∠PAB=∠PAC(角平分线的定义)
∠ABP=∠ACP
AP=AP((公共边)
∴△ APB ≌△APC(AAS)
∴PB=PC(全等三角形对应边相等)
角平分线地性质:角平分线上的点到角两边的距离相等.
符号语言:
∵OC平分∠AOB,
且CD⊥OA,CE⊥OB,
∴CD=CE.
例7 如图,AB//CD,PB和PC平分∠ABC∠DCB,AD过点 P,且与 AB垂直。
求证: PA=PD
证明:如图,作PE⊥BC于点E
∵ AB∥CD(已知)
∴∠BAD+∠CDA=180°(_两直线平行,同旁内角互补_)
∵AD⊥AB
∴∠BAD=90°
∴∠CDA=180°-∠BAD=180°-90°=90°
∴AD⊥CD(角平分线上的点到角两边的距离相等)
∵PB平分∠ABC
∴PA=PE
∴PA=PE=PD
随堂演练
1.已知:如图,AD垂直平分BC,D为垂足.DM⊥AC,DN⊥AB,M,N分别为垂足.
求证:DM=DN.
2.通过学习我们已经知道三角形的三条内角平分线是交于一点的.如图,P是△ABC的内角平分线的交点,已知P点到AB边的距离为1,△ABC的周长为10,则△ABC的面积为______.
P
【解析】∵P是△ABC的内角平分线的交点,
∴P到三边的距离相等,即到三边的距离都是1,
∴S△ABC=S△APC+S△APB+S△BPC
=×1×AC+×1×BC+×1×AB
=×1×(AC+BC+AB)
=×1×10=5.
所以△ABC的面积是5.
故填空答案:5.
六、课堂检测
1.下列条件中,能判定△ABC≌△DEF的是 ( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,∠C=∠F,AC=DE
C.∠A=∠D,∠B=∠E,∠C=∠F
D.AB=DE,BC=EF,△ABC的周长=△DEF的周长
答案D
2.给出下列四个条件,不能判断△ABC≌△A′B′C′的是( )
①∠B=∠B′②∠C=∠C′ ③AC=A′C′ ④BC=B′C′.
A.①②③ B.①②④ C.①③④ D.②③④
答案C、
3.如图,已知相交直线AB和CD,及另一直线MN,如果要在MN上找出与AB、CD距离相等的点,则这样的点至少有______个,最多有______个.
【解析】如图所示,分别作∠AOD及∠AOC的平分线OE与OF,
∵OE与OF分别是∠AOD及∠AOC的平分线,
∴直线OE与OF上的点到AB、CD距离相等,
∴点M必在直线OE或直线OF上,
∵点M在直线MN上,
∴点M在这两条角平分线与直线MN的交点上,
∴当OF或OE与MN平行时,符合条件的点有1个;
当OF或OE均与直线MN不平行时,符合条件的点有2个.
故答案为:1,2.
4.直角△ABC中,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E,若AC=6,
BC=8,AB=10,CD=3.
(1)求DE的长;(2)求△ADB的面积
解:(1)∵AD平分∠CAB,∴∠CAD=∠EAD,
∵DE⊥AB,∠C=90°,∴∠C=∠DEA=90°,
又∵AD为公共边,∴△ACD≌△AED,
∴CD=DE,∵CD=3,∴DE=3;
∵AB=10,
5.如图,E、D分别是AC、AB上的一点,∠EBC、∠BCD的角平分线交于点M,∠BED、∠EDC的角平分线交于N.
求证:A、M、N在一条直线上.
证明:过点N作NF⊥AB于F,NH⊥ED于H,NK⊥AC于K;过点M作MJ⊥BC于J,MP⊥AB于P,MQ⊥AC于Q.
∵EN平分∠BED,DN平分∠EDC,
∴NF=NH,NH=NK,
∴NF=NK,
∴N在∠A的平分线上.
∵BM平分∠ABC,CM平分∠ACB
∴MP=MJ,MQ=MJ,
∴MP=MQ,
∴M在∠A的平分线上.
∵M、N都在∠A的平分线上,
∴A、M、N在一条直线上.
七、课堂小结,作业布置
小结:
1.全等三角形的判定定理:AAS
2.角平分线的性质
作业:课本P36页第1、2、3、4 题
教材分析
全等三角形是几何图形部分的重要内容之一,帮助学生了解全等三角形判定是对简单的平面图形的进一步研究,也是后续研究多边形的性质,三角函数等知识的基础,在平面几何中有着非常重要的地位和作用。
学情分析
首先是学生的知识特征,八年级的学生已经学习了全等三角形的概念和性质。但是学生对数学语言的理解还有待提高,如何判定两个三角形全等,需要老师积极引导。
然后是学生的心理特征,八年级的学生好奇心重,求知欲强,教师通过合适的方法引入有助于他们更好地三角形的相关内容。
教学目标
知识与技能
1.掌握三角形全等的判定定理(AAS)
2.理解角平分线的性质。
过程与方法:在学习过程中培养自主探究能力和严谨的数学思维。
情感态度与价值观:能够体会数学严谨的推理,利用三角形全等解决现实问题,感受数学的乐趣
教学重难点
重点:本节教学的重点是两个三角形全等的条件:两角及其中一个角的对边对应相等的两个三角形全等
难点:例题中需要添加辅助线,证明的思路较复杂,是本节教学的难点
教学方法、手段
教学方法:讲授法、探究法
教学手段:板书与多媒体课件相结合
教学过程
回顾旧知:
到目前为止,我们已学过哪些方法判定两三角形全等?
1. 全等三角形的定义
能够完全重合的两个三角形全等
2.边边边公理(SSS)
三边对应相等的两个三角形全等
3.边角边公理(SAS)
两边及其夹角对应相等的两个三角形全等
4.角边角公理(ASA)
两个角和这两个角的夹边对应相等的两个三角形全等。
二、思考讨论
已知两个三角形中,有两个角和其中一个角的对边对应相等,那么两个三角形是否全等?
探究:在△ABC和△DEF中, ∠A=∠D, ∠B=∠E,BC=EF, △ABC和△DEF全等吗?为什么?
证明:∵ ∠A=∠D, ∠B=∠E(已知)
∴∠C=∠F(三角形内角和定理)
在△ABC和△DEF中
∠B=∠E
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
你能从上题中得到什么结论?
两角及一角的对边对应相等的两个三角形全等
三、讲授新课:
判定三角形全等的定理4:
两角及一角的对边对应相等的两个三角形全等 (简写成“角角边”或“AAS”)
数学语言表示:
在△ABC和△DEF中,
∵ ∠C=∠
∠A=∠D,
AB=DE ,
∴ △ABC≌△DEF(AAS)
必须按照角角边的顺序书写
角角边的情形包括下面两种情况
例题精讲
例6 已知:如图,P是∠BAC的平分线上的一点,PB⊥AB于点B,PC⊥AC于点C.
求证:PB=PC.
证明:
∵PB⊥AB,PC⊥AC(已知)
∴∠ABP=∠ACP=Rt∠(_垂线的定义)
在△APB与△APC中,
∵∠PAB=∠PAC(角平分线的定义)
∠ABP=∠ACP
AP=AP((公共边)
∴△ APB ≌△APC(AAS)
∴PB=PC(全等三角形对应边相等)
角平分线地性质:角平分线上的点到角两边的距离相等.
符号语言:
∵OC平分∠AOB,
且CD⊥OA,CE⊥OB,
∴CD=CE.
例7 如图,AB//CD,PB和PC平分∠ABC∠DCB,AD过点 P,且与 AB垂直。
求证: PA=PD
证明:如图,作PE⊥BC于点E
∵ AB∥CD(已知)
∴∠BAD+∠CDA=180°(_两直线平行,同旁内角互补_)
∵AD⊥AB
∴∠BAD=90°
∴∠CDA=180°-∠BAD=180°-90°=90°
∴AD⊥CD(角平分线上的点到角两边的距离相等)
∵PB平分∠ABC
∴PA=PE
∴PA=PE=PD
随堂演练
1.已知:如图,AD垂直平分BC,D为垂足.DM⊥AC,DN⊥AB,M,N分别为垂足.
求证:DM=DN.
2.通过学习我们已经知道三角形的三条内角平分线是交于一点的.如图,P是△ABC的内角平分线的交点,已知P点到AB边的距离为1,△ABC的周长为10,则△ABC的面积为______.
P
【解析】∵P是△ABC的内角平分线的交点,
∴P到三边的距离相等,即到三边的距离都是1,
∴S△ABC=S△APC+S△APB+S△BPC
=×1×AC+×1×BC+×1×AB
=×1×(AC+BC+AB)
=×1×10=5.
所以△ABC的面积是5.
故填空答案:5.
六、课堂检测
1.下列条件中,能判定△ABC≌△DEF的是 ( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,∠C=∠F,AC=DE
C.∠A=∠D,∠B=∠E,∠C=∠F
D.AB=DE,BC=EF,△ABC的周长=△DEF的周长
答案D
2.给出下列四个条件,不能判断△ABC≌△A′B′C′的是( )
①∠B=∠B′②∠C=∠C′ ③AC=A′C′ ④BC=B′C′.
A.①②③ B.①②④ C.①③④ D.②③④
答案C、
3.如图,已知相交直线AB和CD,及另一直线MN,如果要在MN上找出与AB、CD距离相等的点,则这样的点至少有______个,最多有______个.
【解析】如图所示,分别作∠AOD及∠AOC的平分线OE与OF,
∵OE与OF分别是∠AOD及∠AOC的平分线,
∴直线OE与OF上的点到AB、CD距离相等,
∴点M必在直线OE或直线OF上,
∵点M在直线MN上,
∴点M在这两条角平分线与直线MN的交点上,
∴当OF或OE与MN平行时,符合条件的点有1个;
当OF或OE均与直线MN不平行时,符合条件的点有2个.
故答案为:1,2.
4.直角△ABC中,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E,若AC=6,
BC=8,AB=10,CD=3.
(1)求DE的长;(2)求△ADB的面积
解:(1)∵AD平分∠CAB,∴∠CAD=∠EAD,
∵DE⊥AB,∠C=90°,∴∠C=∠DEA=90°,
又∵AD为公共边,∴△ACD≌△AED,
∴CD=DE,∵CD=3,∴DE=3;
∵AB=10,
5.如图,E、D分别是AC、AB上的一点,∠EBC、∠BCD的角平分线交于点M,∠BED、∠EDC的角平分线交于N.
求证:A、M、N在一条直线上.
证明:过点N作NF⊥AB于F,NH⊥ED于H,NK⊥AC于K;过点M作MJ⊥BC于J,MP⊥AB于P,MQ⊥AC于Q.
∵EN平分∠BED,DN平分∠EDC,
∴NF=NH,NH=NK,
∴NF=NK,
∴N在∠A的平分线上.
∵BM平分∠ABC,CM平分∠ACB
∴MP=MJ,MQ=MJ,
∴MP=MQ,
∴M在∠A的平分线上.
∵M、N都在∠A的平分线上,
∴A、M、N在一条直线上.
七、课堂小结,作业布置
小结:
1.全等三角形的判定定理:AAS
2.角平分线的性质
作业:课本P36页第1、2、3、4 题
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
