浙教版 七年级数学上册 1.4 有理数的大小比较 课件(共26张PPT)
文档属性
| 名称 | 浙教版 七年级数学上册 1.4 有理数的大小比较 课件(共26张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
1.4 有理数的大小比较
数学(浙教版)
七年级 上册
第1章 有理数
学习目标
1.掌握有理数的大小比较方法;
2.学会用数轴来比较有理数的大小;
3、掌握有理数大小比较的实际应用;
导入新课
比较下列物体的大小
讲授新课
知识点一 直接比较有理数的大小
结论:
(1)正数大于0,
(2)两个负数,绝对值大的反而小.
例如,1 > 0,0 > -1,1 > -1,-1 > -2.
负数小于0,
正数大于负数;
问题:
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
运用法则比较有理数的大小
讲授新课
典例精析
【例1】在实数-(-3),-4,0,|-2|中,最小的数是( )
A.-(-3) B.-4 C.0 D.|-2|
【详解】解:∵-(-3)=3,|-2|=2,
∴-4<0<2<3,
∴-4<0<|-2|<-(-3),
∴最小的数是-4,
故选:B.
讲授新课
练一练
1.比较大小:
(1)-(-5) -(+6) . (2) .
【答案】 > /大于 > /大于
【点睛】本题考查了有理数的大小比较,解题关键是掌握有理数大小比较法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
讲授新课
2.已知|a|=,|b|=,求a,b的值,并比较它们的大小.
【详解】解:|a|= ,|b|= ,
∴a=±,b=±.
当a=时,a>b;
当a=时,a<b.
讲授新课
知识点二 利用数轴比较有理数的大小
下图表示某一天我国5个城市的最低气温。
武汉5 ℃ 北京-10℃ 上海0℃ 广州10℃ 哈尔滨-20℃
问题:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
-20 -10 0 5 10
●
●
●
●
●
借助数轴比较有理数的大小
讲授新课
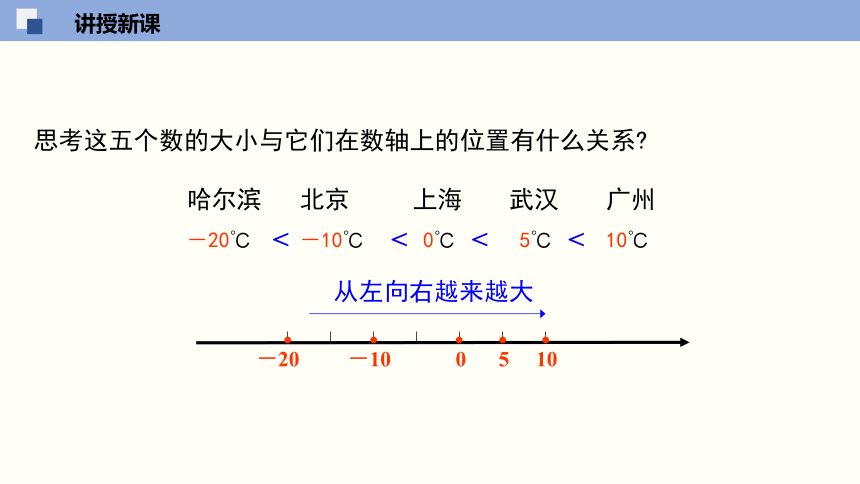
思考这五个数的大小与它们在数轴上的位置有什么关系
从左向右越来越大
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
-20 -10 0 5 10
●
●
●
●
●
讲授新课
有理数大小的比较方法2---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
-5 -4 -3 -2 -1 0 1 2 3 4 5
小 大
有没有最大的有理数 有没有最小的有理数 为什么
讲授新课
典例精析
【例2】将下列四个数表示在数轴上,它们对应的点中,离原点最近的是( )
A.-0.3 B. C.3 D.-3
【详解】∵|-0.3|=0.3,||=,|3|=3,|-3|=3,,3>>0.3,
∴|-3|=|3|>| |>|-0.3|,
∴-0.3离原点最近.
故选A.
讲授新课
练一练
1.如图,若A是实数a在数轴上对应的点,请比较a,-a,1的大小关系(用“<”连接): .
【详解】由数轴的定义可得:0<a<1
则-1<-a<0
有理数的大小比较法则:正数大于0,负数小于0,正数大于负数,负数绝对值大的反而小
则-a<a<1
故答案为:-a<a<1.
讲授新课
2.画一条数轴,并下列各数的数轴上表示出来,并用“<”把这些数连接起来.
,0 ,2 ,-3 ,3.5 .
【详解】解:如图所示:
∴-3<<0<2<3.5
讲授新课
典例精析
【例3】1月24日,北方13个省会城市气温创今冬以米新低.其中,长春-27.3℃,沈阳-21.8℃,呼和浩特-28,6℃,太原-19.4℃.四个城市中,气温最低的是( )
A.长春 B.沈阳 C.呼和浩特 D.太原
【详解】解:∵28.6>27.3>21.8>19.4,
∴-28.6<-27.3<-21.8<-19.4,
∴呼和浩特的气温最低.
故选C.
知识点三 有理数比较大小的实际应用
讲授新课
练一练
1.希望小学要买60个足球,现有甲、乙、丙三个商店可以选择,三个商店足球单价都是30元,但各个商店的优惠办法不同:
甲店:全部打八折销售;
乙店:当购买足球不超过20个时,不打折;购买超过20个时,超过部分打六折;
丙店:买10个足球免费赠送2个,不足10个不赠送;
为了节省费用,希望小学应到哪个商店购买合算?为什么?
讲授新课
【详解】解:为了节省费用,希望小学应到乙商店购买合算.
理由:由题意可得,
在甲店购买需要花费为:30×60×0.8=1440(元),
在乙店购买需要花费为:30×20+30×(60﹣20)×0.6=1320(元),
在丙店购买需要花费为:30×50=1500(元),
∵1320<1440<1500,
∴为了节省费用,希望小学应到乙商店购买合算.
当堂检测
1.下列各数中,比-2小的数为( )
A.-4 B.0 C.2 D.4
【详解】解:A、-2<0,-4<0,|-4|>|-2|,
∴-4<-2,本选项符合题意;
B、0>-2,本选项不符合题意;
C、2>-2,本选项不符合题意;
D、4>-2,本选项不符合题意.
故选:A.
当堂检测
2.下列结论正确的是( )
A.如果a>b,那么|a|>|b| B.如果|a|>|b|,那么a>b
C.如果|a|=|b|,那么a=b D.如果a=b,那么|a|=|b|
【详解】解:A.如果a>b,当a=0,b=-1时,|a|<|b|,故A选项错误,不符合题意;
B.如果|a|>|b|,当a=-1,b=0时,a<b,故B选项错误,不符合题意;
C.如果|a|=|b|,当a,b互为相反数时,a≠b,故C选项错误,不符合题意;
D.如果a=b,那么|a|=|b|,故D选项正确,符合题意.
故选:D.
当堂检测
3.大于且小于1的整数是 .
【详解】如图:
大于且小于1的整数有:-1,0,
故答案为:-1,0.
当堂检测
4.有理数a<0,b>0,且|a|<|b|,把a,-a,b,-b按由小到大的顺序排列是 .
【详解】解:∵a<0,b>0,且|a|<|b|,
∴-a>0,-b<0,且-b<a,-a<b,
∴把a,-a,b,-b按由小到大的顺序排列是-b<a<-a<b,
故答案为:-b<a<-a<b.
当堂检测
5.已知实数m,n在数轴上的对应点的位置如图所示,则m n.(填“<”、“>”或“=”)
【详解】解: m在n的左边,
∴m<n,
故答案为:<.
当堂检测
6.在数轴上表示下列各数:0,-1,,-1.5,|-3|,-(-2),并用“<”号连接.
【详解】解:|-3|=3,-(-2)=2,如图所示:
故-1.5<-1<0<<-(-2)<|-3|.
当堂检测
7.已知|x|=2,|y|=3,|z|=4,且x>y>z .求x ,y,z的值.
【详解】解:∵|x|=2,|y|=3,|z|=4,
∴x=±2,y=±3,z=±4,
∵x>y>z,
∴x=2,y=-3,z=-4 或 x=-2,y=-3,z=-4.
当堂检测
8.有理数a,b,c在数轴上的位置如图:
(1)比较b-c与b-a的大小;
(2)若|a+3|=0,|b-1|=0,|c-4|=0,求a+2b-3c的值.
【详解】(1)解:观察数轴可知:a<0<b<c
故b-c<0,b-a>0
故b-c<b-a.
(2)由题可知:
a+3=0,b-1=0,c-4=0解得:a=-3,b=1,c=4,
则a+2b-3c=-13.
课堂小结
比较有理数大小的方法:
方法①:数轴上表示的两个数,右边的总比左边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
谢 谢~
1.4 有理数的大小比较
数学(浙教版)
七年级 上册
第1章 有理数
学习目标
1.掌握有理数的大小比较方法;
2.学会用数轴来比较有理数的大小;
3、掌握有理数大小比较的实际应用;
导入新课
比较下列物体的大小
讲授新课
知识点一 直接比较有理数的大小
结论:
(1)正数大于0,
(2)两个负数,绝对值大的反而小.
例如,1 > 0,0 > -1,1 > -1,-1 > -2.
负数小于0,
正数大于负数;
问题:
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
运用法则比较有理数的大小
讲授新课
典例精析
【例1】在实数-(-3),-4,0,|-2|中,最小的数是( )
A.-(-3) B.-4 C.0 D.|-2|
【详解】解:∵-(-3)=3,|-2|=2,
∴-4<0<2<3,
∴-4<0<|-2|<-(-3),
∴最小的数是-4,
故选:B.
讲授新课
练一练
1.比较大小:
(1)-(-5) -(+6) . (2) .
【答案】 > /大于 > /大于
【点睛】本题考查了有理数的大小比较,解题关键是掌握有理数大小比较法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
讲授新课
2.已知|a|=,|b|=,求a,b的值,并比较它们的大小.
【详解】解:|a|= ,|b|= ,
∴a=±,b=±.
当a=时,a>b;
当a=时,a<b.
讲授新课
知识点二 利用数轴比较有理数的大小
下图表示某一天我国5个城市的最低气温。
武汉5 ℃ 北京-10℃ 上海0℃ 广州10℃ 哈尔滨-20℃
问题:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
-20 -10 0 5 10
●
●
●
●
●
借助数轴比较有理数的大小
讲授新课
思考这五个数的大小与它们在数轴上的位置有什么关系
从左向右越来越大
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
-20 -10 0 5 10
●
●
●
●
●
讲授新课
有理数大小的比较方法2---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
-5 -4 -3 -2 -1 0 1 2 3 4 5
小 大
有没有最大的有理数 有没有最小的有理数 为什么
讲授新课
典例精析
【例2】将下列四个数表示在数轴上,它们对应的点中,离原点最近的是( )
A.-0.3 B. C.3 D.-3
【详解】∵|-0.3|=0.3,||=,|3|=3,|-3|=3,,3>>0.3,
∴|-3|=|3|>| |>|-0.3|,
∴-0.3离原点最近.
故选A.
讲授新课
练一练
1.如图,若A是实数a在数轴上对应的点,请比较a,-a,1的大小关系(用“<”连接): .
【详解】由数轴的定义可得:0<a<1
则-1<-a<0
有理数的大小比较法则:正数大于0,负数小于0,正数大于负数,负数绝对值大的反而小
则-a<a<1
故答案为:-a<a<1.
讲授新课
2.画一条数轴,并下列各数的数轴上表示出来,并用“<”把这些数连接起来.
,0 ,2 ,-3 ,3.5 .
【详解】解:如图所示:
∴-3<<0<2<3.5
讲授新课
典例精析
【例3】1月24日,北方13个省会城市气温创今冬以米新低.其中,长春-27.3℃,沈阳-21.8℃,呼和浩特-28,6℃,太原-19.4℃.四个城市中,气温最低的是( )
A.长春 B.沈阳 C.呼和浩特 D.太原
【详解】解:∵28.6>27.3>21.8>19.4,
∴-28.6<-27.3<-21.8<-19.4,
∴呼和浩特的气温最低.
故选C.
知识点三 有理数比较大小的实际应用
讲授新课
练一练
1.希望小学要买60个足球,现有甲、乙、丙三个商店可以选择,三个商店足球单价都是30元,但各个商店的优惠办法不同:
甲店:全部打八折销售;
乙店:当购买足球不超过20个时,不打折;购买超过20个时,超过部分打六折;
丙店:买10个足球免费赠送2个,不足10个不赠送;
为了节省费用,希望小学应到哪个商店购买合算?为什么?
讲授新课
【详解】解:为了节省费用,希望小学应到乙商店购买合算.
理由:由题意可得,
在甲店购买需要花费为:30×60×0.8=1440(元),
在乙店购买需要花费为:30×20+30×(60﹣20)×0.6=1320(元),
在丙店购买需要花费为:30×50=1500(元),
∵1320<1440<1500,
∴为了节省费用,希望小学应到乙商店购买合算.
当堂检测
1.下列各数中,比-2小的数为( )
A.-4 B.0 C.2 D.4
【详解】解:A、-2<0,-4<0,|-4|>|-2|,
∴-4<-2,本选项符合题意;
B、0>-2,本选项不符合题意;
C、2>-2,本选项不符合题意;
D、4>-2,本选项不符合题意.
故选:A.
当堂检测
2.下列结论正确的是( )
A.如果a>b,那么|a|>|b| B.如果|a|>|b|,那么a>b
C.如果|a|=|b|,那么a=b D.如果a=b,那么|a|=|b|
【详解】解:A.如果a>b,当a=0,b=-1时,|a|<|b|,故A选项错误,不符合题意;
B.如果|a|>|b|,当a=-1,b=0时,a<b,故B选项错误,不符合题意;
C.如果|a|=|b|,当a,b互为相反数时,a≠b,故C选项错误,不符合题意;
D.如果a=b,那么|a|=|b|,故D选项正确,符合题意.
故选:D.
当堂检测
3.大于且小于1的整数是 .
【详解】如图:
大于且小于1的整数有:-1,0,
故答案为:-1,0.
当堂检测
4.有理数a<0,b>0,且|a|<|b|,把a,-a,b,-b按由小到大的顺序排列是 .
【详解】解:∵a<0,b>0,且|a|<|b|,
∴-a>0,-b<0,且-b<a,-a<b,
∴把a,-a,b,-b按由小到大的顺序排列是-b<a<-a<b,
故答案为:-b<a<-a<b.
当堂检测
5.已知实数m,n在数轴上的对应点的位置如图所示,则m n.(填“<”、“>”或“=”)
【详解】解: m在n的左边,
∴m<n,
故答案为:<.
当堂检测
6.在数轴上表示下列各数:0,-1,,-1.5,|-3|,-(-2),并用“<”号连接.
【详解】解:|-3|=3,-(-2)=2,如图所示:
故-1.5<-1<0<<-(-2)<|-3|.
当堂检测
7.已知|x|=2,|y|=3,|z|=4,且x>y>z .求x ,y,z的值.
【详解】解:∵|x|=2,|y|=3,|z|=4,
∴x=±2,y=±3,z=±4,
∵x>y>z,
∴x=2,y=-3,z=-4 或 x=-2,y=-3,z=-4.
当堂检测
8.有理数a,b,c在数轴上的位置如图:
(1)比较b-c与b-a的大小;
(2)若|a+3|=0,|b-1|=0,|c-4|=0,求a+2b-3c的值.
【详解】(1)解:观察数轴可知:a<0<b<c
故b-c<0,b-a>0
故b-c<b-a.
(2)由题可知:
a+3=0,b-1=0,c-4=0解得:a=-3,b=1,c=4,
则a+2b-3c=-13.
课堂小结
比较有理数大小的方法:
方法①:数轴上表示的两个数,右边的总比左边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
谢 谢~
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
