浙教版数学八年级上册2.3.1 等腰三角形性质定理1及等边三角形性质 课件(共21张PPT)
文档属性
| 名称 | 浙教版数学八年级上册2.3.1 等腰三角形性质定理1及等边三角形性质 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 697.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
2.3 等腰三角形的性质定理
第1课时 等腰三角形性质定理1及等边三角形性质
学习目标
掌握等腰三角形的性质定理1;
掌握等边三角形的性质,并会利用其性质进行简单推理.
会利用等腰三角形的性质定理1进行简单的推理计算;
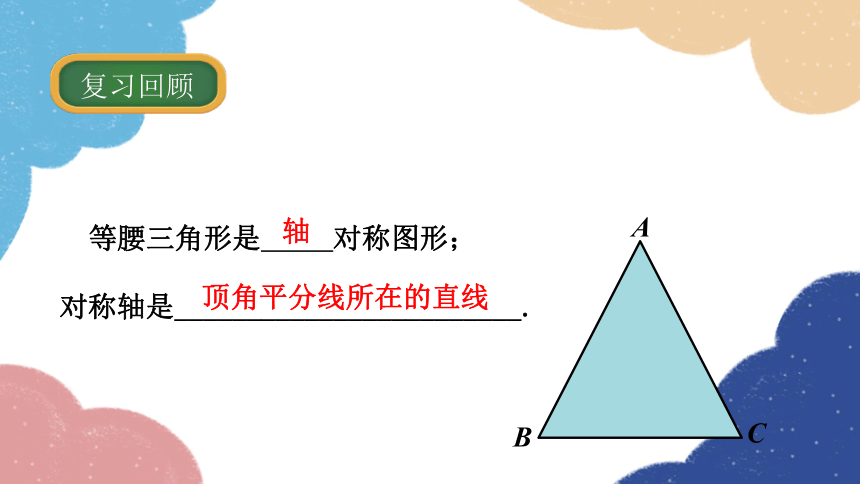
复习回顾
等腰三角形是 对称图形;
对称轴是________________________.
A
B
C
轴
顶角平分线所在的直线
A
B
C
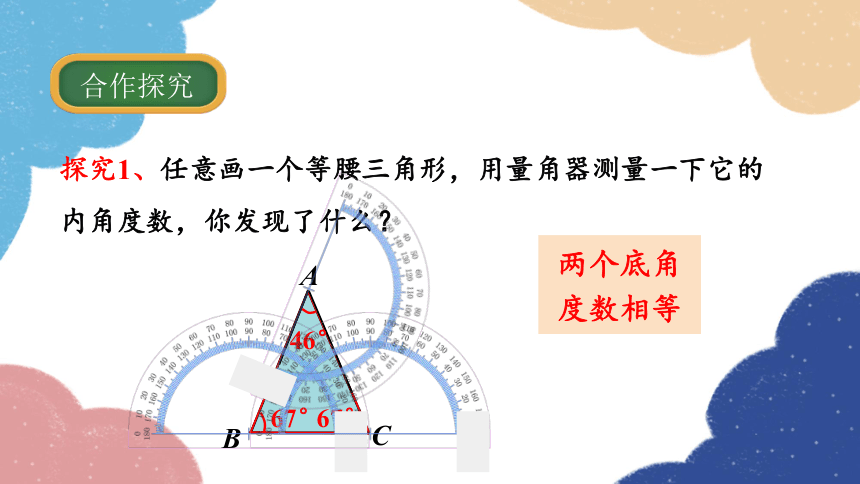
合作探究
探究1、任意画一个等腰三角形,用量角器测量一下它的内角度数,你发现了什么?
67°
67°
46°
两个底角度数相等
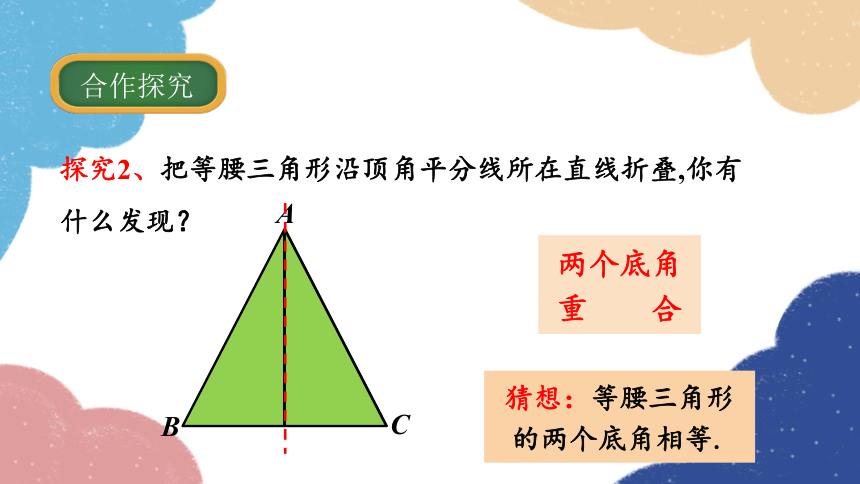
探究2、把等腰三角形沿顶角平分线所在直线折叠,你有什么发现?
B
C
A
合作探究
两个底角
重 合
猜想:等腰三角形的两个底角相等.
验证猜想
已知:△ABC中,AB=AC.求证:∠B=∠C.
证明:作顶角的平分线AD.
在△BAD和△CAD中,
AB=AC ( 已知 ),
∠1=∠2 ( 辅助线作法 ),
AD=AD (公共边) ,
∵
A
B
C
D
1
2
∴ △BAD ≌ △CAD (SAS).
∴ ∠B=∠C (全等三角形的对应角相等).
等腰三角形性质定理1
等腰三角形的两个底角相等.
也就是说,在同一个三角形中,等边对等角.
新课讲解
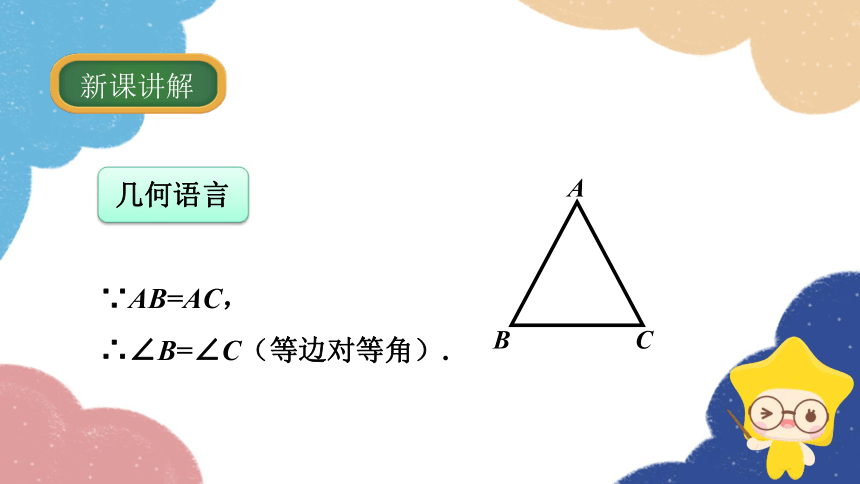
新课讲解
几何语言
A
B
C
∵AB=AC,
∴∠B=∠C(等边对等角).
巩固练习
1、等腰三角形一个底角为70°,它的顶角为______.
2、等腰三角形一个角为70°,它的另外两个角为_______________________.
3、等腰三角形一个角为110°,它的另外两个角为_______________________.
40 °
70°,40°或 55°,55°
35 °,35 °
巩固练习
4、已知等腰△ABC中,∠B=80°,则∠A的度数为_________________.
分析:(1)当∠B为顶角时,根据三角形内角和定理可得,∠A=∠C=50°.
(2)当∠B为底角时,①∠A为顶角,根据三角形内角和定理可得,∠A=20°. ②∠A为底角,∠A=∠B=80°.
50°、20°或80°
注意求内角度数时的分类思想(顶角或底角).
归纳总结
等腰
三角形
内角关系
①顶角+2×底角=180°;
②顶角=180°-2×底角;
③底角=(180°-顶角)÷2;
④0°<顶角<180°;
⑤0°<底角<90°.
例题讲解
例1 求等边三角形ABC三个内角的度数.
A
B
C
等边三角形的每个内角都等于60°.
归纳总结
等边三角形的性质
1、等边三角形的各个内角都等于60°.
2、等边三角形是轴对称图形,它有三条对称轴.
3、等边三角形是特殊的等腰三角形,它具有等腰三角形的一切性质.
例题讲解
例2 求证:等腰三角形两底角的平分线相等.
已知:如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.
求证:BD=CE.
A
B
C
D
E
分析:要证明BD=CE,只需证明△BCE ≌ △CBD .因为BC是△BCE 和△CBD 的公共边,所以只需证明∠ABC= ∠ACB, ∠BCE=∠CBD.这可由已知AB=AC,BD和CE是△ABC的两条角平分线得到.
A
B
C
D
E
课内练习
1、如图,在△ABC中,AB=AC,∠ACD=100°,则∠A=________.
A
B
C
D
100°
?
20 °
分析:由题意知,∠ACB=∠B=80°,由三角形内角和定理得,∠A=20°.
2、已知:如图,在△ABC中,AB=AC,P为BC的中点,D,E分别是AB,AC上的点,且AD=AE.
求证:PD=PE.
A
B
C
D
E
P
证明:∵ AB=AC, AD=AE,
∴∠B=∠C,BD=CE.
又∵ P为BC的中点,∴BP=CP.
∴ △BDP≌ △CEP (SAS).
∴ PD=PE.
拓展提高
如图,在三角形ABC中,AB=AC,D在AC上,且BD=BC=AD,求△ABC各内角的度数?
分析: 根据等边对等角可得角度相等,再结合三角形的外角性质及内角和定理即可求出各角的度数.
A
C
B
D
1
2
3
证明:∵ BD=BC=AD, AB=AC,
∴∠1=∠A,∠3=∠C=∠ABC,
又∵∠3=∠1+∠A,
∴∠3=2∠1,
∴∠ABC=2∠1,即∠1=∠2,
∴在△BDC中,∠3+∠2+∠C=180°,即5∠2=180°,
解得,∠2=36°.
∴在△ABC中,∠A=∠2=36°,∠C=∠ABC=72°.
A
C
B
D
1
2
3
知识
1、等腰三角形的两个底角相等.
2、等边三角形的各个内角都等于60 °.
能力
1、进行有关角度的计算(分类讨论思想).
2、进行简单的推理论证.
经验
1、证角等,找全等,巧构造.
2、证角等,找等腰,巧转化.
课堂小结
感谢观看!
2.3 等腰三角形的性质定理
第1课时 等腰三角形性质定理1及等边三角形性质
学习目标
掌握等腰三角形的性质定理1;
掌握等边三角形的性质,并会利用其性质进行简单推理.
会利用等腰三角形的性质定理1进行简单的推理计算;
复习回顾
等腰三角形是 对称图形;
对称轴是________________________.
A
B
C
轴
顶角平分线所在的直线
A
B
C
合作探究
探究1、任意画一个等腰三角形,用量角器测量一下它的内角度数,你发现了什么?
67°
67°
46°
两个底角度数相等
探究2、把等腰三角形沿顶角平分线所在直线折叠,你有什么发现?
B
C
A
合作探究
两个底角
重 合
猜想:等腰三角形的两个底角相等.
验证猜想
已知:△ABC中,AB=AC.求证:∠B=∠C.
证明:作顶角的平分线AD.
在△BAD和△CAD中,
AB=AC ( 已知 ),
∠1=∠2 ( 辅助线作法 ),
AD=AD (公共边) ,
∵
A
B
C
D
1
2
∴ △BAD ≌ △CAD (SAS).
∴ ∠B=∠C (全等三角形的对应角相等).
等腰三角形性质定理1
等腰三角形的两个底角相等.
也就是说,在同一个三角形中,等边对等角.
新课讲解
新课讲解
几何语言
A
B
C
∵AB=AC,
∴∠B=∠C(等边对等角).
巩固练习
1、等腰三角形一个底角为70°,它的顶角为______.
2、等腰三角形一个角为70°,它的另外两个角为_______________________.
3、等腰三角形一个角为110°,它的另外两个角为_______________________.
40 °
70°,40°或 55°,55°
35 °,35 °
巩固练习
4、已知等腰△ABC中,∠B=80°,则∠A的度数为_________________.
分析:(1)当∠B为顶角时,根据三角形内角和定理可得,∠A=∠C=50°.
(2)当∠B为底角时,①∠A为顶角,根据三角形内角和定理可得,∠A=20°. ②∠A为底角,∠A=∠B=80°.
50°、20°或80°
注意求内角度数时的分类思想(顶角或底角).
归纳总结
等腰
三角形
内角关系
①顶角+2×底角=180°;
②顶角=180°-2×底角;
③底角=(180°-顶角)÷2;
④0°<顶角<180°;
⑤0°<底角<90°.
例题讲解
例1 求等边三角形ABC三个内角的度数.
A
B
C
等边三角形的每个内角都等于60°.
归纳总结
等边三角形的性质
1、等边三角形的各个内角都等于60°.
2、等边三角形是轴对称图形,它有三条对称轴.
3、等边三角形是特殊的等腰三角形,它具有等腰三角形的一切性质.
例题讲解
例2 求证:等腰三角形两底角的平分线相等.
已知:如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.
求证:BD=CE.
A
B
C
D
E
分析:要证明BD=CE,只需证明△BCE ≌ △CBD .因为BC是△BCE 和△CBD 的公共边,所以只需证明∠ABC= ∠ACB, ∠BCE=∠CBD.这可由已知AB=AC,BD和CE是△ABC的两条角平分线得到.
A
B
C
D
E
课内练习
1、如图,在△ABC中,AB=AC,∠ACD=100°,则∠A=________.
A
B
C
D
100°
?
20 °
分析:由题意知,∠ACB=∠B=80°,由三角形内角和定理得,∠A=20°.
2、已知:如图,在△ABC中,AB=AC,P为BC的中点,D,E分别是AB,AC上的点,且AD=AE.
求证:PD=PE.
A
B
C
D
E
P
证明:∵ AB=AC, AD=AE,
∴∠B=∠C,BD=CE.
又∵ P为BC的中点,∴BP=CP.
∴ △BDP≌ △CEP (SAS).
∴ PD=PE.
拓展提高
如图,在三角形ABC中,AB=AC,D在AC上,且BD=BC=AD,求△ABC各内角的度数?
分析: 根据等边对等角可得角度相等,再结合三角形的外角性质及内角和定理即可求出各角的度数.
A
C
B
D
1
2
3
证明:∵ BD=BC=AD, AB=AC,
∴∠1=∠A,∠3=∠C=∠ABC,
又∵∠3=∠1+∠A,
∴∠3=2∠1,
∴∠ABC=2∠1,即∠1=∠2,
∴在△BDC中,∠3+∠2+∠C=180°,即5∠2=180°,
解得,∠2=36°.
∴在△ABC中,∠A=∠2=36°,∠C=∠ABC=72°.
A
C
B
D
1
2
3
知识
1、等腰三角形的两个底角相等.
2、等边三角形的各个内角都等于60 °.
能力
1、进行有关角度的计算(分类讨论思想).
2、进行简单的推理论证.
经验
1、证角等,找全等,巧构造.
2、证角等,找等腰,巧转化.
课堂小结
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
