浙教版七年级数学上册 2.1 有理数的加法(第1课时) 教学课件(共33张PPT)
文档属性
| 名称 | 浙教版七年级数学上册 2.1 有理数的加法(第1课时) 教学课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 22:32:29 | ||
图片预览








文档简介
(共33张PPT)
2.1 有理数的加法
第1课时 有理数的加法
数学(浙教版)
七年级 上册
第2章 有理数的运算
学习目标
1、掌握有理数加法的意义,理解有理数加法法则;
2、学会运用有理数的加法法则进行运算;
3、探索体会有理数加法的运算过程,掌握有理数加法在实际生活中的应用.
导入新课
→东
小明在一条东西向的跑道上,先走了20米,又走了30米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米
有哪几种情况,说一说。
讲授新课
知识点一 有理数的加法运算
→东
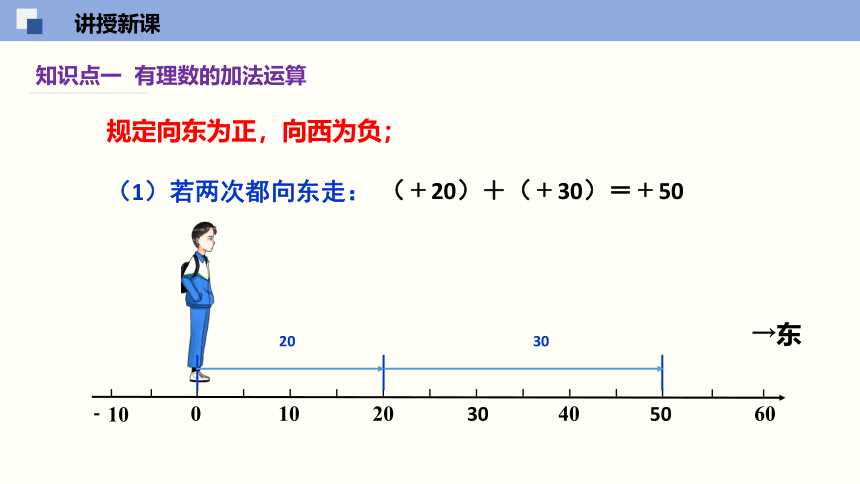
规定向东为正,向西为负;
(1)若两次都向东走:
30
20
10
40
0
50
﹣10
60
20
30
(﹢20)+(﹢30)=﹢50
讲授新课
→东
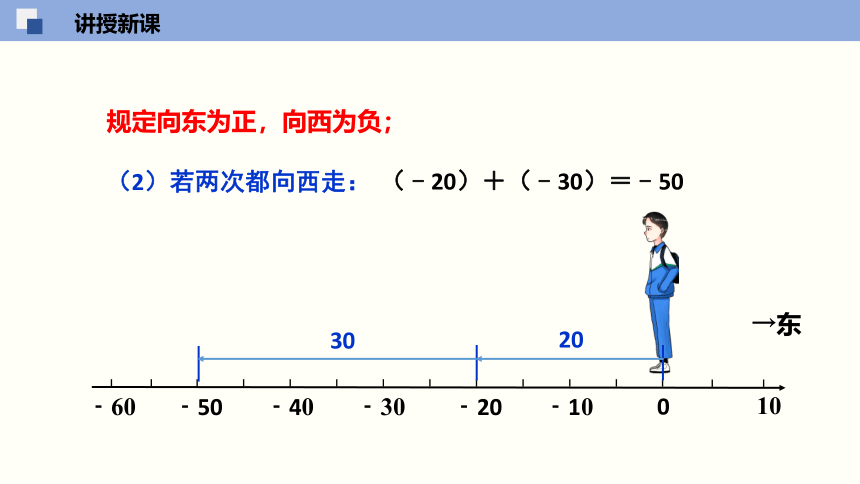
规定向东为正,向西为负;
(2)若两次都向西走:
﹣20
﹣30
﹣40
﹣10
﹣50
0
﹣60
10
20
30
(﹣20)+(﹣30)=﹣50
讲授新课
→东
规定向东为正,向西为负;
(3)若第一次向东走20米,第二次向西走30米:
10
0
﹣10
20
﹣20
30
﹣30
40
20
30
(﹢20)+(﹣30)=﹣10
讲授新课
→东
规定向东为正,向西为负;
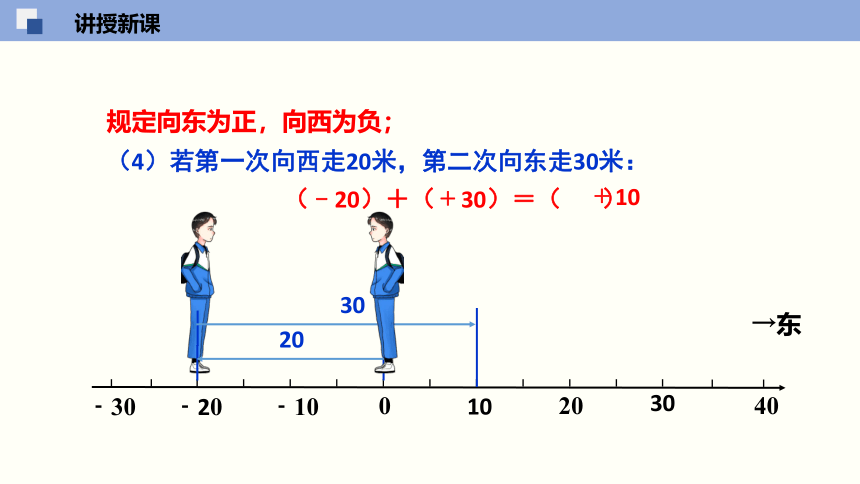
(4)若第一次向西走20米,第二次向东走30米:
10
0
﹣10
20
﹣20
30
﹣30
40
20
30
(﹣20)+(﹢30)=( )
﹢10
讲授新课
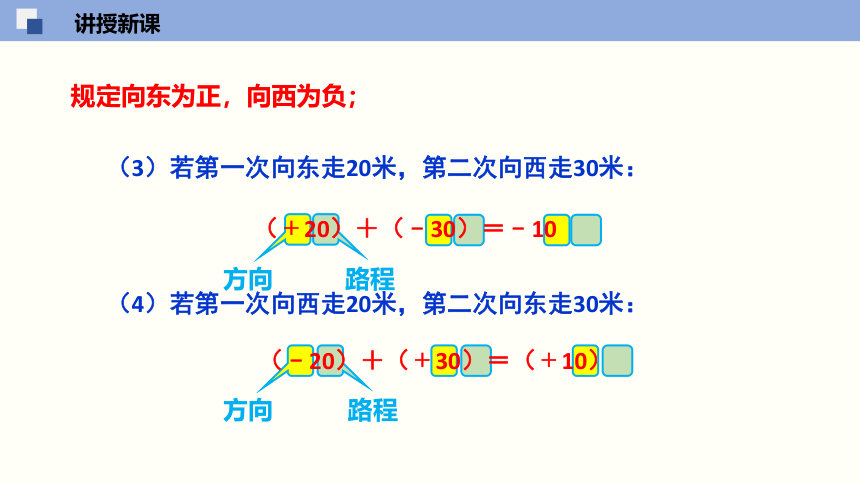
(3)若第一次向东走20米,第二次向西走30米:
(﹢20)+(﹣30)=﹣10
(4)若第一次向西走20米,第二次向东走30米:
(﹣20)+(﹢30)=(﹢10)
规定向东为正,向西为负;
方向
路程
方向
路程
讲授新课
规定向东为正,向西为负;
(5)若第一次向西走30米,第二次向东走30米:
(﹣30)+(﹢30)=( )
0
(6)若第一次向西走30米,第二次没走:
(﹣30)+0=( )
﹣30
讲授新课
-2 + (+3) = +(3-2)
-3 + (+2)= -(3-2)
-2 + (+2)= (2-2)
比一比
加数
加数
和
加数异号
加数的绝对值不相等
你从上面三个式子中发现了什么?
讲授新课
概念归纳
(1)
(﹢20)+(﹢30)=﹢50
(2)
(﹣20)+(﹣30)=﹣50
(3)
(﹢20)+(﹣30)=﹣10
(4)
(﹣20)+(﹢30)=﹢10
(5)
(﹣30)+(﹢30)= 0
(﹣30)+0=﹣30
(6)
有理数加法法则
1.同号两数相加
取__________的正负号,并把___________;
取__________________的正负号,并__________________________
________;
3.互为相反数的两个数相加_____;
4.一个数与零相加,___________.
2.异号两数相加
加数相同
绝对值相加
绝对值较大的加数
用较大的绝对值减去较小的绝对值
得零
仍得这个数
讲授新课
同号两数相加,取相同的符号,并把绝对值相加.
有理数加法法则一:
有理数加法法则二:
异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
讲授新课
典例精析
【例1】下列各式计算正确的是( )
A.(-3)+(-3)=0 B.0+(-5)=-5
C.(-10)+(+7)=+17 D.(-3)+(-7)=-4
【详解】解:A.(-3)+(-3)=-6 ,原计算错误,不符合题意;
B.0+(-5)=-5 ,原计算正确,符合题意;
C.(-10)+(+7)=-3,原计算错误,不符合题意;
D.(-3)+(-7)=-10,原计算错误,不符合题意;
故选:B.
讲授新课
练一练
1.不小于-3而小于2的所有负整数的和是 .
【详解】解:∵不小于-3而小于2的负整数有-3,-2,-1,
∴这些整数的和为:-3+(-2)+(-1)=-6.
故答案为:-6.
讲授新课
2.计算:
(1)(-2)+(+3)+(+4)+(-3)+(+5)+(-4);
(2)()+()+()+()
【详解】(1)解:原式=3
(2)解:原式=-7+3=-4
典例精析
【例2】如果a+b+c<0,那么a,b,c三个数中( )
A.有一个数必为0 B.至少有一个负数
C.有且只有一个负数 D.至少有两个负数
【详解】解:∵a+b+c<0,
∴a,b,c三个数中必然会有负数,即a,b,c三个数中至少有一个负数,
故选B.
讲授新课
知识点二 有理数加法运算的符号问题
讲授新课
练一练
1.用“>”或“<”填空:
(1)如果a>0,b>0,那么a+b______0;
(2)如果a<0,b<0,那么a+b______0;
(3)如果a>0,b<0,|a|>|b|,那么a+b______0;
(4)如果a>0,b<0,|a|<|b|,那么a+b______0.
【详解】(1)同号两数相加,取相同的符号,两数都为正数,所以两数的和为正.
(2)同号两数相加,取相同的符号,两数都为负数,所以两数的和为负.
(3)异号两数相加,取绝对值较大的加数的符号,由于|a|>|b|,所以两数的和取a的符号,即两数和的符号为正.
(4)异号两数相加,取绝对值较大的加数的符号,由于|a|<|b|,所以两数的和取b的符号,即两数和的符号为负.
讲授新课
知识点三 有理数加法运算的实际应用
讲授新课
典例精析
【例3】如图,小明在某运动APP中,设定了每天的步数目标为8000步.该APP用目标线上方或下方的柱状图表示每天超过或少于目标数的步数,如14日,小明少于目标数的步数为500步,则从13日到16日这四天中小明一共走的步数为( )
A.27200 B.32000 C.35800 D.36800
【详解】解:从13日到16日这四天中小明一共走的步数为
8000×4+1038-500+1262+2000=35800(步).故选:C.
知识点三 有理数加法运算的实际应用
讲授新课
练一练
1.甲、乙、丙三地海拔高度分别为25米,-16米,-10米,那么最高的地方比最低的地方高 米.
【详解】 25-(-16)=41(米)
故答案为:41
讲授新课
2.红星面粉厂3天内面粉进、出库的吨数如下(“+”表示进库,“-”表示出库):
+26,-32,-15,+34,-38,-20.
(1)经过3天,仓库里的面粉是增加了还是减少了?
(2)经过这3天,仓库管理员结算时发现库里还有280吨面粉,那么3天前仓库里有面粉多少吨?
【详解】(1)解:26+(-32)+(-15)+34+(-38)+(-20)=-45(吨).
答:经过3天,仓库里的面粉减少了.
(2)280-(-45)=325(吨).
答:3天前仓库里有面粉325吨.
(3)(|+26|+|-32|+|-15|+|+34|+|-38|+|-20|)×6=990(元).
答:这3天要付990元的装卸费.
当堂检测
1.计算7+(-3)的结果是( )
A.-10 B.-4 C.4 D.10
【详解】解:7+(-3)=4.
故选:C.
当堂检测
2.若a,b,c均为正数,则a+b-c,b+c-a,c+a-b这三个数中出现负数的情况是( )
A.不可能有负数 B.必有一个负数
C.至多有一个负数 D.可能有两个负数
【详解】解:显然当a=1,b=1,c=3时,有1+1-3<0,1+3-1>0,1+3-1>0,所以排除A.
当a=b=c=1时,没有负数,故B错误,
对于D,若假设有两个负数,则不防设:
a+b<c①,b+c<a②,
由①+②可得:b<0,与已知条件矛盾,
∴假设错误,不可能有两个负数,
同理a+b-c,b+c-a,c+a-b中不可能有3个负数,
故选:C.
当堂检测
3.一个数比 7的绝对值大1,另一个数比2的相反数小1,则这两个数的和为( )
A.5 B.8 C.9 D.11
【详解】解:根据题意得两数分别为|-7|+1=7+1=8,(-2)-1=-3,
故两数的和为8+(-3)=5.
故选A.
当堂检测
4.绝对值小于8的所有整数的和等于 .
【详解】绝对值小于8的所有整数有-7,-6,-5,-4,-3,-2,
-1,0,1,2,3,4,5,6,7.
绝对值小于8的所有整数的和等于0,
故答案为:0.
当堂检测
5.设[x]表示不超过x的最大整数,计算[-2.3]+[6.5]=: .
【详解】解:∵[x]表示不超过x的最大整数,
∴[-2.3]=-3;[6.5]=6,
∴[-2.3]+[6.5]=-3+6=3;
故答案为3.
当堂检测
6.学校、张明家、书店依次坐落在一条南北走向的大街上,学校在张明家的南边20米处,书店在张明家的北边100米处,张明同学从家出发,向北走了50米,接着又向北走了-70米,则此时张明在 .
【详解】把张明家记为原点,北方向记为正,南方向记为负,则学校记为-20m,书店记为+100m,根据题意得:
张明从家向北走的距离为:+50+(-70)=-20(m),
∴此时张明在家的南边20米处,即学校的位置.
故答案为:家的南边20米处(或学校)
当堂检测
7.计算.
(1)(-3)+(+40)+(-32)+(-8);
(2)()+()+()+(-8.25);
(3)(+5.6)+(-0.9)+(+4.4)+(-8.1)+(-1);
(4)(-0.5)+()+(+2.75)+().
当堂检测
【详解】(1)原式=-3+40-40=0;
(2)原式=(+)+(-8.25)=7+(-9)=2;
(3)原式=(5.6+4.4)+(-0.9-8.1)+(-1)=10+(-9)+(-1)=0;
(4)原式=(-0.5)+()++2.75=-6+6=0.
当堂检测
8.在一条不完整的数轴上,有A、P两点,其中点A表示数-3,设点P表示的数为m,用n表示A、P表示数的和.
(1)若m=2,求n的值;
(2)当PA=4时,求m的值.
【详解】(1)解:∵点A表示数-3,m=2,
∴n=2+(-3)=-1;
(2)解:∵A点表示数-3,PA=4,
∴当点P在点A的右侧时,点P表示的数m=-3=4=1,
当点P在A的左侧时,P点表示的数m=-3-4=-7.
当堂检测
9.已知|a|=5,|b|=4.若a<b,求a+b的值;
【详解】由题意得a=±5,b=±4,
又∵a<b,
∴a=-5 b=4,或a=-5,b=-4,
∴a+b=-5+4=-1或a+b=-5+(-4)=-9.
综上所述,a+b的值为-1或-9.
课堂小结
(1)同号两数相加,结果取相同符号,并把绝对值相加.
(2)异号两数相加,结果取绝对值较大的加数的符号,并将较大的绝对值减较小的绝对值。互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
有理数的加法法则
谢 谢~
2.1 有理数的加法
第1课时 有理数的加法
数学(浙教版)
七年级 上册
第2章 有理数的运算
学习目标
1、掌握有理数加法的意义,理解有理数加法法则;
2、学会运用有理数的加法法则进行运算;
3、探索体会有理数加法的运算过程,掌握有理数加法在实际生活中的应用.
导入新课
→东
小明在一条东西向的跑道上,先走了20米,又走了30米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米
有哪几种情况,说一说。
讲授新课
知识点一 有理数的加法运算
→东
规定向东为正,向西为负;
(1)若两次都向东走:
30
20
10
40
0
50
﹣10
60
20
30
(﹢20)+(﹢30)=﹢50
讲授新课
→东
规定向东为正,向西为负;
(2)若两次都向西走:
﹣20
﹣30
﹣40
﹣10
﹣50
0
﹣60
10
20
30
(﹣20)+(﹣30)=﹣50
讲授新课
→东
规定向东为正,向西为负;
(3)若第一次向东走20米,第二次向西走30米:
10
0
﹣10
20
﹣20
30
﹣30
40
20
30
(﹢20)+(﹣30)=﹣10
讲授新课
→东
规定向东为正,向西为负;
(4)若第一次向西走20米,第二次向东走30米:
10
0
﹣10
20
﹣20
30
﹣30
40
20
30
(﹣20)+(﹢30)=( )
﹢10
讲授新课
(3)若第一次向东走20米,第二次向西走30米:
(﹢20)+(﹣30)=﹣10
(4)若第一次向西走20米,第二次向东走30米:
(﹣20)+(﹢30)=(﹢10)
规定向东为正,向西为负;
方向
路程
方向
路程
讲授新课
规定向东为正,向西为负;
(5)若第一次向西走30米,第二次向东走30米:
(﹣30)+(﹢30)=( )
0
(6)若第一次向西走30米,第二次没走:
(﹣30)+0=( )
﹣30
讲授新课
-2 + (+3) = +(3-2)
-3 + (+2)= -(3-2)
-2 + (+2)= (2-2)
比一比
加数
加数
和
加数异号
加数的绝对值不相等
你从上面三个式子中发现了什么?
讲授新课
概念归纳
(1)
(﹢20)+(﹢30)=﹢50
(2)
(﹣20)+(﹣30)=﹣50
(3)
(﹢20)+(﹣30)=﹣10
(4)
(﹣20)+(﹢30)=﹢10
(5)
(﹣30)+(﹢30)= 0
(﹣30)+0=﹣30
(6)
有理数加法法则
1.同号两数相加
取__________的正负号,并把___________;
取__________________的正负号,并__________________________
________;
3.互为相反数的两个数相加_____;
4.一个数与零相加,___________.
2.异号两数相加
加数相同
绝对值相加
绝对值较大的加数
用较大的绝对值减去较小的绝对值
得零
仍得这个数
讲授新课
同号两数相加,取相同的符号,并把绝对值相加.
有理数加法法则一:
有理数加法法则二:
异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
讲授新课
典例精析
【例1】下列各式计算正确的是( )
A.(-3)+(-3)=0 B.0+(-5)=-5
C.(-10)+(+7)=+17 D.(-3)+(-7)=-4
【详解】解:A.(-3)+(-3)=-6 ,原计算错误,不符合题意;
B.0+(-5)=-5 ,原计算正确,符合题意;
C.(-10)+(+7)=-3,原计算错误,不符合题意;
D.(-3)+(-7)=-10,原计算错误,不符合题意;
故选:B.
讲授新课
练一练
1.不小于-3而小于2的所有负整数的和是 .
【详解】解:∵不小于-3而小于2的负整数有-3,-2,-1,
∴这些整数的和为:-3+(-2)+(-1)=-6.
故答案为:-6.
讲授新课
2.计算:
(1)(-2)+(+3)+(+4)+(-3)+(+5)+(-4);
(2)()+()+()+()
【详解】(1)解:原式=3
(2)解:原式=-7+3=-4
典例精析
【例2】如果a+b+c<0,那么a,b,c三个数中( )
A.有一个数必为0 B.至少有一个负数
C.有且只有一个负数 D.至少有两个负数
【详解】解:∵a+b+c<0,
∴a,b,c三个数中必然会有负数,即a,b,c三个数中至少有一个负数,
故选B.
讲授新课
知识点二 有理数加法运算的符号问题
讲授新课
练一练
1.用“>”或“<”填空:
(1)如果a>0,b>0,那么a+b______0;
(2)如果a<0,b<0,那么a+b______0;
(3)如果a>0,b<0,|a|>|b|,那么a+b______0;
(4)如果a>0,b<0,|a|<|b|,那么a+b______0.
【详解】(1)同号两数相加,取相同的符号,两数都为正数,所以两数的和为正.
(2)同号两数相加,取相同的符号,两数都为负数,所以两数的和为负.
(3)异号两数相加,取绝对值较大的加数的符号,由于|a|>|b|,所以两数的和取a的符号,即两数和的符号为正.
(4)异号两数相加,取绝对值较大的加数的符号,由于|a|<|b|,所以两数的和取b的符号,即两数和的符号为负.
讲授新课
知识点三 有理数加法运算的实际应用
讲授新课
典例精析
【例3】如图,小明在某运动APP中,设定了每天的步数目标为8000步.该APP用目标线上方或下方的柱状图表示每天超过或少于目标数的步数,如14日,小明少于目标数的步数为500步,则从13日到16日这四天中小明一共走的步数为( )
A.27200 B.32000 C.35800 D.36800
【详解】解:从13日到16日这四天中小明一共走的步数为
8000×4+1038-500+1262+2000=35800(步).故选:C.
知识点三 有理数加法运算的实际应用
讲授新课
练一练
1.甲、乙、丙三地海拔高度分别为25米,-16米,-10米,那么最高的地方比最低的地方高 米.
【详解】 25-(-16)=41(米)
故答案为:41
讲授新课
2.红星面粉厂3天内面粉进、出库的吨数如下(“+”表示进库,“-”表示出库):
+26,-32,-15,+34,-38,-20.
(1)经过3天,仓库里的面粉是增加了还是减少了?
(2)经过这3天,仓库管理员结算时发现库里还有280吨面粉,那么3天前仓库里有面粉多少吨?
【详解】(1)解:26+(-32)+(-15)+34+(-38)+(-20)=-45(吨).
答:经过3天,仓库里的面粉减少了.
(2)280-(-45)=325(吨).
答:3天前仓库里有面粉325吨.
(3)(|+26|+|-32|+|-15|+|+34|+|-38|+|-20|)×6=990(元).
答:这3天要付990元的装卸费.
当堂检测
1.计算7+(-3)的结果是( )
A.-10 B.-4 C.4 D.10
【详解】解:7+(-3)=4.
故选:C.
当堂检测
2.若a,b,c均为正数,则a+b-c,b+c-a,c+a-b这三个数中出现负数的情况是( )
A.不可能有负数 B.必有一个负数
C.至多有一个负数 D.可能有两个负数
【详解】解:显然当a=1,b=1,c=3时,有1+1-3<0,1+3-1>0,1+3-1>0,所以排除A.
当a=b=c=1时,没有负数,故B错误,
对于D,若假设有两个负数,则不防设:
a+b<c①,b+c<a②,
由①+②可得:b<0,与已知条件矛盾,
∴假设错误,不可能有两个负数,
同理a+b-c,b+c-a,c+a-b中不可能有3个负数,
故选:C.
当堂检测
3.一个数比 7的绝对值大1,另一个数比2的相反数小1,则这两个数的和为( )
A.5 B.8 C.9 D.11
【详解】解:根据题意得两数分别为|-7|+1=7+1=8,(-2)-1=-3,
故两数的和为8+(-3)=5.
故选A.
当堂检测
4.绝对值小于8的所有整数的和等于 .
【详解】绝对值小于8的所有整数有-7,-6,-5,-4,-3,-2,
-1,0,1,2,3,4,5,6,7.
绝对值小于8的所有整数的和等于0,
故答案为:0.
当堂检测
5.设[x]表示不超过x的最大整数,计算[-2.3]+[6.5]=: .
【详解】解:∵[x]表示不超过x的最大整数,
∴[-2.3]=-3;[6.5]=6,
∴[-2.3]+[6.5]=-3+6=3;
故答案为3.
当堂检测
6.学校、张明家、书店依次坐落在一条南北走向的大街上,学校在张明家的南边20米处,书店在张明家的北边100米处,张明同学从家出发,向北走了50米,接着又向北走了-70米,则此时张明在 .
【详解】把张明家记为原点,北方向记为正,南方向记为负,则学校记为-20m,书店记为+100m,根据题意得:
张明从家向北走的距离为:+50+(-70)=-20(m),
∴此时张明在家的南边20米处,即学校的位置.
故答案为:家的南边20米处(或学校)
当堂检测
7.计算.
(1)(-3)+(+40)+(-32)+(-8);
(2)()+()+()+(-8.25);
(3)(+5.6)+(-0.9)+(+4.4)+(-8.1)+(-1);
(4)(-0.5)+()+(+2.75)+().
当堂检测
【详解】(1)原式=-3+40-40=0;
(2)原式=(+)+(-8.25)=7+(-9)=2;
(3)原式=(5.6+4.4)+(-0.9-8.1)+(-1)=10+(-9)+(-1)=0;
(4)原式=(-0.5)+()++2.75=-6+6=0.
当堂检测
8.在一条不完整的数轴上,有A、P两点,其中点A表示数-3,设点P表示的数为m,用n表示A、P表示数的和.
(1)若m=2,求n的值;
(2)当PA=4时,求m的值.
【详解】(1)解:∵点A表示数-3,m=2,
∴n=2+(-3)=-1;
(2)解:∵A点表示数-3,PA=4,
∴当点P在点A的右侧时,点P表示的数m=-3=4=1,
当点P在A的左侧时,P点表示的数m=-3-4=-7.
当堂检测
9.已知|a|=5,|b|=4.若a<b,求a+b的值;
【详解】由题意得a=±5,b=±4,
又∵a<b,
∴a=-5 b=4,或a=-5,b=-4,
∴a+b=-5+4=-1或a+b=-5+(-4)=-9.
综上所述,a+b的值为-1或-9.
课堂小结
(1)同号两数相加,结果取相同符号,并把绝对值相加.
(2)异号两数相加,结果取绝对值较大的加数的符号,并将较大的绝对值减较小的绝对值。互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
有理数的加法法则
谢 谢~
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
