2.6 直角三角形分层作业（含解析）

中小学教育资源及组卷应用平台
2.6直角三角形 同步分层作业
基础过关
1．在Rt△ABC中，∠C＝90°，∠B＝38°，则∠A的度数为（　　）
A．38° B．42° C．52° D．62°
2．如图，在△ABC中，∠A+∠B＝90°，D为AB边的中点，若AB＝8，则CD＝（　　）
A．3 B．4 C．5 D．
3．在△ABC中，∠C＝90°，∠A＝2∠B，则∠A的度数是（　　）
A．45° B．30° C．90° D．60°
4．如图，在Rt△ABC中，CD是斜边AB上的中线，若∠A＝20°，则∠BDC＝（　　）
A．30° B．40° C．45° D．60°
5．在下列条件中不能判定△ABC为直角三角形的是（　　）
A．∠A＝90°﹣∠C B．∠A＝∠B﹣∠C C．∠A＝2∠B＝3∠C D．∠A＝∠B＝∠C
6．如图，两条公路AC，BC恰好互相垂直，公路AB的中点M与点C被湖隔开．若测得AM的长为0.9km，则M，C两点间的距离为（　　）
A．0.5km B．0.6km C．0.9km D．1.2km
7．如图，一根竹竿AB，斜靠在竖直的墙上，点P是AB中点，A′B′表示竹竿AB及在竹竿AB滑动过程中的情况是（　　）
A．下滑时，OP的长度增大 B．上升时，OP的长度减小
C．只要滑动，OP端沿墙向下滑动过程中的某个位置，则OP的长的长度就变化
D．无论怎样滑动，OP的长度不变
8．如图，在△ABC中，∠ACB＝90°，CD是高，∠B＝60°，若BD＝1，则AD＝（　　）
A．2 B． C．3 D．
9．如图，∠ACB＝90°，CD⊥AB于点D．若∠ACD＝35°，则∠ABC的度数是 　 　．
10．在Rt△ABC中，CD是斜边AB上的中线，若CD＝1，则AB＝　　．
11．如图，在Rt△ABC中，CD是斜边AB上的中线，∠A＝20度，则∠BCD＝　　度．
12．在△ABC中，∠A+∠B＝90°，∠C＝3∠B，若AB＝6，则AC＝　 　．
13.对于下列问题，在解答过程的空白处填上适当的内容（理由或数学式）．如图．
在直角△ABC中，CD是斜边AB上的高，∠BCD＝35°．
（1）求∠EBC的度数；
（2）求∠A的度数．
解：（1）∵CD⊥AB（已知），
∴∠CDB＝　 　°，
∵∠EBC＝∠CDB+∠BCD（ 　 　），
∴∠EBC＝　 　°+35°＝　 　°．（等量代换），
（2）∠EBC＝∠A+∠ACB（ 　 　），
∴∠A＝∠EBC﹣　 　（等式的性质），
∵∠ACB＝90°（已知），
∴∠A＝　 　﹣90°＝　 　°（等量代换）．
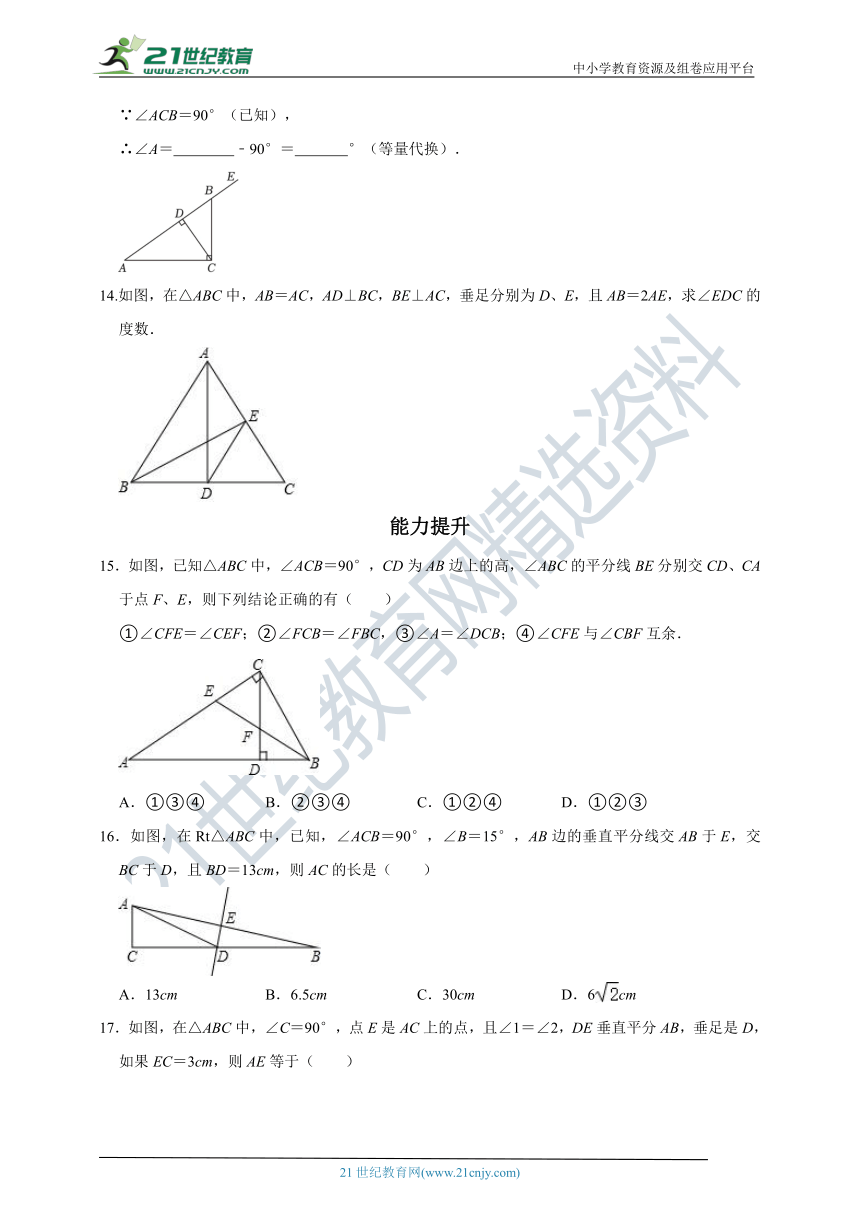
14.如图，在△ABC中，AB＝AC，AD⊥BC，BE⊥AC，垂足分别为D、E，且AB＝2AE，求∠EDC的度数．
能力提升
15．如图，已知△ABC中，∠ACB＝90°，CD为AB边上的高，∠ABC的平分线BE分别交CD、CA于点F、E，则下列结论正确的有（　　）
①∠CFE＝∠CEF；②∠FCB＝∠FBC，③∠A＝∠DCB；④∠CFE与∠CBF互余．
A．①③④ B．②③④ C．①②④ D．①②③
16．如图，在Rt△ABC中，已知，∠ACB＝90°，∠B＝15°，AB边的垂直平分线交AB于E，交BC于D，且BD＝13cm，则AC的长是（　　）
A．13cm B．6.5cm C．30cm D．6cm
17．如图，在△ABC中，∠C＝90°，点E是AC上的点，且∠1＝∠2，DE垂直平分AB，垂足是D，如果EC＝3cm，则AE等于（　　）
A．3cm B．4cm C．6cm D．9cm
18．如图，在△ABC中，∠CAB＝90°，边BC的垂直平分线交AC于点D，交BC于点E．若∠CBD＝2∠ABD，则∠C的度数为 　 　．
19．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，∠ACD＝3∠BCD，E是斜边AB的中点，∠ECD是　 　度．
20．如图，在△ABC中，BA＝BC，∠ABC＝120°，BD⊥BC交AC于点D，BD＝，则AC的长 　3　．

21．如图，已知∠AOB＝60°，点P在边OA上，OP＝16，点M、N在边OB上，PM＝PN，若MN＝4，则OM＝　 　．
22．如图，在△ABC中，∠BAC＝90°，AD⊥BC于点D，BE平分∠ABC，AD、BE相交于点F．
（1）若∠CAD＝36°，求∠AEF的度数；
（2）试说明：∠AEF＝∠AFE．
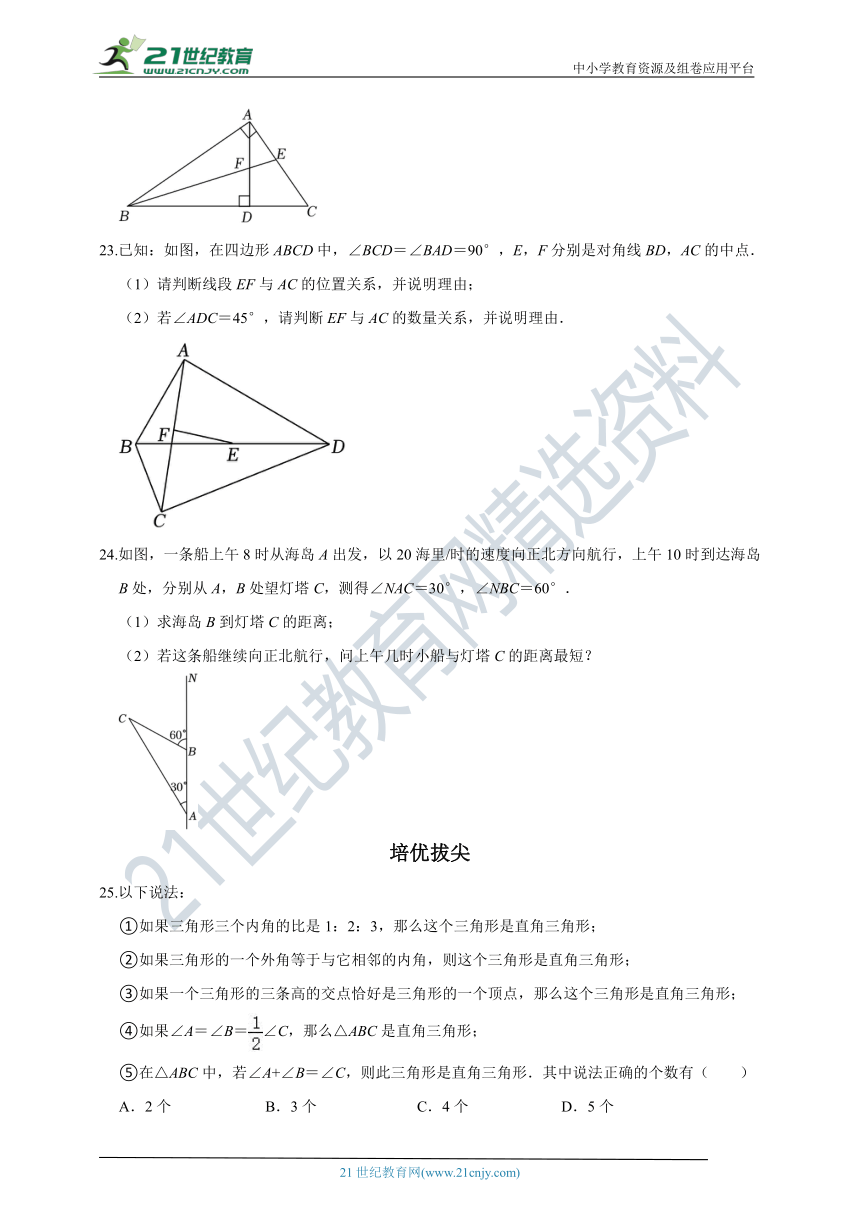
23.已知：如图，在四边形ABCD中，∠BCD＝∠BAD＝90°，E，F分别是对角线BD，AC的中点．
（1）请判断线段EF与AC的位置关系，并说明理由；
（2）若∠ADC＝45°，请判断EF与AC的数量关系，并说明理由．
24.如图，一条船上午8时从海岛A出发，以20海里/时的速度向正北方向航行，上午10时到达海岛B处，分别从A，B处望灯塔C，测得∠NAC＝30°，∠NBC＝60°．
（1）求海岛B到灯塔C的距离；
（2）若这条船继续向正北航行，问上午几时小船与灯塔C的距离最短？
培优拔尖
25.以下说法：
①如果三角形三个内角的比是1：2：3，那么这个三角形是直角三角形；
②如果三角形的一个外角等于与它相邻的内角，则这个三角形是直角三角形；
③如果一个三角形的三条高的交点恰好是三角形的一个顶点，那么这个三角形是直角三角形；
④如果∠A＝∠B＝∠C，那么△ABC是直角三角形；
⑤在△ABC中，若∠A+∠B＝∠C，则此三角形是直角三角形．其中说法正确的个数有（　　）
A．2个 B．3个 C．4个 D．5个
26．已知非Rt△ABC中，∠A＝60°，高BD和CE所在的直线相交于点H，求∠BHC的度数为（　　）
A．60° B．60°或150° C．120° D．60°或120°
27．如果等腰三角形一条边上的高等于这条边长的一半，那么这个等腰三角形的顶角的度数是 　　．
28．如图，已知锐角△ABC中，CD、BE分别是AB、AC边上的高，M、N分别是线段BC、DE的中点．
（1）求证：MN⊥DE；
（2）若∠ABC＝70°，∠ACB＝50°，连结DM、ME，求∠DME的度数；
（3）猜想∠DME与∠A之间的关系，并证明你的猜想．
29.如图，在△ABC中，AB＝AC，∠BAC＝120°，AD是BC边上的中线，且BD＝BE，CD的垂直平分线MF交AC于F，交BC于M，MF的长为2．
（1）求∠ADE的度数；
（2）△ADF是正三角形吗？为什么？
（3）求AB的长．
30．如图，△ABC是边长为4的等边三角形，点P在AB上，过点P作PE⊥AC，垂足为E，延长BC到点Q，使CQ＝PA，连接PQ交AC于点D，求DE的长．
31.如图，在△ABC中，∠C＝90°，∠A＝30°，AB＝4cm，动点P、Q同时从A、B两点出发，分别在AB、BC边上匀速移动，它们的速度分别为VP＝2cm/s，VQ＝1cm/s，当点P到达点B时，P、Q两点同时停止运动，设点P的运动时间为ts．
（1）当t为何值时，△PBQ为等边三角形？
（2）当t为何值时，△PBQ为直角三角形？
答案与解析
基础过关
1．在Rt△ABC中，∠C＝90°，∠B＝38°，则∠A的度数为（　　）
A．38° B．42° C．52° D．62°
【思路点拨】根据直角三角形两锐角互余可得∠A+∠B＝90°，再代入∠B的度数可得∠A的度数．
【解析】解：∵∠C＝90°，
∴∠A+∠B＝90°，
∵∠B＝38°，
∴∠A＝52°，
故选：C．
【点睛】此题主要考查了直角三角形的性质，关键是掌握在直角三角形中，两个锐角互余．
2．如图，在△ABC中，∠A+∠B＝90°，D为AB边的中点，若AB＝8，则CD＝（　　）
A．3 B．4 C．5 D．
【思路点拨】首先可得△ABC是直角三角形，由直角三角形斜边上中线的性质即可求得结果．
【解析】解：∵∠A+∠B＝90°，
∴∠C＝90°，即△ABC是直角三角形，
∵D为AB边的中点，且AB＝8，
∴；
故选：B．
【点睛】本题考查了直角三角形的判定，直角三角形斜边中线的性质，掌握这两个知识点是关键．
3．在△ABC中，∠C＝90°，∠A＝2∠B，则∠A的度数是（　　）
A．45° B．30° C．90° D．60°
【思路点拨】在直角三角形中，两个锐角互余，由此即可求解．
【解析】解：在△ABC中，∠C＝90°，
∴∠A+∠B＝90°，
∵∠A＝2∠B，
∴3∠B＝90°，
∴∠B＝30°，
∴∠A＝2∠B＝60°，
故选：D．
【点睛】本题考查直角三角形的性质，关键是掌握直角三角形两锐角互余．
4．如图，在Rt△ABC中，CD是斜边AB上的中线，若∠A＝20°，则∠BDC＝（　　）
A．30° B．40° C．45° D．60°
【思路点拨】根据直角三角形斜边上中线定理得出CD＝AD，求出∠DCA＝∠A，根据三角形的外角性质求出求出即可．
【解析】解：∵∠ACB＝90°，CD是斜边AB上的中线，
∴BD＝CD＝AD，
∴∠A＝∠DCA＝20°，
∴∠BDC＝∠A+∠DCA＝20°+20°＝40°．
故选：B．
【点睛】本题考查了对三角形的外角性质，直角三角形斜边上的中线性质，等腰三角形性质等知识点的理解和运用，能求出BD＝CD＝AD和∠DCA的度数是解此题的关键．
5．在下列条件中不能判定△ABC为直角三角形的是（　　）
A．∠A＝90°﹣∠C B．∠A＝∠B﹣∠C C．∠A＝2∠B＝3∠C D．∠A＝∠B＝∠C
【思路点拨】根据三角形内角和定理和各选项中的条件计算出△ABC的内角，然后根据直角三角形的判定方法进行判断．
【解析】解：A、∵∠A＝90°﹣∠C，
∴∠A+∠C＝90°，
∴∠B＝90°，
∴△ABC是直角三角形，故选项不符合题意；
B、∵∠A＝∠B﹣∠C，
∴∠A+∠C＝∠B，
∵∠A+∠C+∠B＝180°，
∴2∠B＝180°，
∴∠B＝90°，
∴△ABC是直角三角形，故选项不符合题意；
C、∵∠A＝2∠B＝3∠C，
设∠A＝x，
∴∠B＝x，∠C＝x，
∵∠A+∠B+∠C＝180°，
∴x+x+x＝180°，
解得x＝（）°＞90°，
∴△ABC不是直角三角形，故选项符合题意；
D、∵∠A＝∠B＝∠C，
设∠A＝∠B＝x，
∴∠C＝2x，
∵∠A+∠B+∠C＝180°，
∴x+x+2x＝180°，
解得x＝45°，
∴∠C＝2x＝90°，
∴△ABC是直角三角形，故选项不符合题意．
故选：C．
【点睛】本题考查了三角形内角和定理以及直角三角形的判定，解题的关键是掌握三角形的内角和等于180°并灵活运用．
6．如图，两条公路AC，BC恰好互相垂直，公路AB的中点M与点C被湖隔开．若测得AM的长为0.9km，则M，C两点间的距离为（　　）
A．0.5km B．0.6km C．0.9km D．1.2km
【思路点拨】根据直角三角形斜边上的中线等于斜边的一半即可解答．
【解析】解：∵公路AC，BC互相垂直，
∴∠ACB＝90°，
∴△ABC是直角三角形，
∵公路AB的中点M与点C被湖隔开，
若测得AM的长为0.9km，
∴，
即M、C两点间的距离为0.9km．
故选：C．
【点睛】本题主要考查了直角三角形的性质，熟记直角三角形斜边上的中线等于斜边的一半是解题的关键．
7．如图，一根竹竿AB，斜靠在竖直的墙上，点P是AB中点，A′B′表示竹竿AB及在竹竿AB滑动过程中的情况是（　　）
A．下滑时，OP的长度增大 B．上升时，OP的长度减小
C．只要滑动，OP端沿墙向下滑动过程中的某个位置，则OP的长的长度就变化
D．无论怎样滑动，OP的长度不变
【思路点拨】根据直角三角形斜边上的中线性质得出答案即可．
【解析】解：∵∠AOB＝90°，P为AB的中点，
∴OP＝AB，
即OP的长在竹竿AB滑动过程中始终保持不变，
故选：D．
【点睛】本题考查了直角三角形斜边上的中线和两点之间的距离，能熟记直角三角形斜边上的中线等于斜边的一半是解此题的关键．
8．如图，在△ABC中，∠ACB＝90°，CD是高，∠B＝60°，若BD＝1，则AD＝（　　）
A．2 B． C．3 D．
【思路点拨】利用30°所对的直角边是斜边的一半，BC＝2BD，AB＝2BC，分别求出BC，AB，利用AD＝AB﹣BD，进行计算即可得解．
【解析】解：在△ABC中，∠ACB＝90°，CD是高，∠B＝60°，
∴∠CDB＝90°，∠A＝∠DCB＝90°﹣∠B＝30°，
∴BC＝2BD＝2，AB＝2BC＝4，
∴AD＝4﹣1＝3；
故选：C．
【点睛】本题考查含30°角直角三角形．熟练掌握30°角所对的直角边是斜边的一半，是解题的关键．
9．如图，∠ACB＝90°，CD⊥AB于点D．若∠ACD＝35°，则∠ABC的度数是 　35°　．
【思路点拨】由已知条件，根据垂直定义求出∠BDC＝90°，从而根据直角三角形两锐角互余得∠ABC+∠BCD＝90°，∠ACD+∠BCD＝90°，最后根据余角的性质即可得到答案．
【解析】解：∵CD⊥AB于点D，
∴∠BDC＝90°，
∴∠ABC+∠BCD＝90°，
∵∠ACB＝90°，
∴∠ACD+∠BCD＝90°，
∴∠ABC＝∠ACD＝35°，
故答案为：35°．
【点睛】此题主要考查的是直角三角形的性质和余角的性质，解题关键是根据已知条件找出∠BCD的两个余角．
10．在Rt△ABC中，CD是斜边AB上的中线，若CD＝1，则AB＝　2　．
【思路点拨】利用直角三角形斜边上的中线性质，即可解答．
【解析】解：在Rt△ABC中，CD是斜边AB上的中线，CD＝1，
∴AB＝2CD＝2，
故答案为：2．
【点睛】本题考查了直角三角形斜边上的中线，熟练掌握直角三角形斜边上的中线性质是解题的关键．
11．如图，在Rt△ABC中，CD是斜边AB上的中线，∠A＝20度，则∠BCD＝　70　度．
【思路点拨】在Rt△ABC中，根据CD是斜边AB上的中线，得CD＝AD，可求出∠ACD＝20°即可解决问题．
【解析】解：在Rt△ABC中，
∵CD是斜边AB上的中线，
∴CD＝AD，
∴∠A＝∠ACD＝20°，
∴∠BCD＝∠ACB﹣∠ACD＝90°﹣20°＝70°，
故答案为：70．
【点睛】本题主要考查了直角三角形斜边上的中线等于斜边的一半，以及等腰三角形的性质，熟记性质是解题的关键．
12．在△ABC中，∠A+∠B＝90°，∠C＝3∠B，若AB＝6，则AC＝　 　．
【思路点拨】首先根据角之间的关系可得∠B＝30°，再根据在直角三角形中，30°角所对的直角边等于斜边的一半可得AC＝AB．
【解析】解：∵∠A+∠B＝90°，
∴∠C＝180°﹣90°＝90°，
∵∠C＝3∠B，
∴∠B＝30°，
∵AB＝6，
∴AC＝3，
故答案为：3．
【点睛】此题主要考查了直角三角形的性质，关键是掌握在直角三角形中，30°角所对的直角边等于斜边的一半．
13.对于下列问题，在解答过程的空白处填上适当的内容（理由或数学式）．如图．
在直角△ABC中，CD是斜边AB上的高，∠BCD＝35°．
（1）求∠EBC的度数；
（2）求∠A的度数．
解：（1）∵CD⊥AB（已知），
∴∠CDB＝　90　°，
∵∠EBC＝∠CDB+∠BCD（ 　三角形的一个外角等于与它不相邻的两个内角和　），
∴∠EBC＝　90　°+35°＝　125　°．（等量代换），
（2）∠EBC＝∠A+∠ACB（ 　三角形的一个外角等于与它不相邻的两个内角和　），
∴∠A＝∠EBC﹣　∠ACB　（等式的性质），
∵∠ACB＝90°（已知），
∴∠A＝　125°　﹣90°＝　35　°（等量代换）．
【思路点拨】（1）由垂直的定义可得∠CDB＝90°，利用三角形外角的性质可得可求解∠EBC的度数；
（2）由三角形外角的性质可得∠A＝∠EBC﹣∠ACB，结合∠ACB＝90°可求解∠A的度数．
【解析】解：（1）∵CD⊥AB（已知），
∴∠CDB＝90°．
∵∠EBC＝∠CDB+∠BCD（三角形的一个外角等于与它不相邻的两个内角和）．
∴∠EBC＝90°+35°＝125°（等量代换）．
（2）∵∠EBC＝∠A+∠ACB（三角形的一个外角等于与它不相邻的两个内角和），
∴∠A＝∠EBC﹣∠ACB（等式的性质）．
∵∠ACB＝90°（已知），
∴∠A＝125°﹣90°＝35°（等量代换）．
故答案为（1）90；三角形的一个外角等于与它不相邻的两个内角和；90；125；
（2）三角形的一个外角等于与它不相邻的两个内角和；∠ACB，125°；35．
【点睛】本题主要考查三角形外角的性质，垂直的定义，灵活运用三角形外角的性质是解题的关键．
14.如图，在△ABC中，AB＝AC，AD⊥BC，BE⊥AC，垂足分别为D、E，且AB＝2AE，求∠EDC的度数．
【思路点拨】由垂直的定义得到∠AEB＝∠BEC＝90°，根据直角三角形的性质得到∠ABE＝30°，求得∠BAE＝60°，推出△ABC是等边三角形，得到∠C＝60°，根据直角三角形和等边三角形的性质即可得到结论．
【解析】解：∵BE⊥AC，
∴∠AEB＝∠BEC＝90°，
∵AB＝2AE，
∴∠ABE＝30°，
∴∠BAE＝60°，
∵AB＝AC，
∴△ABC是等边三角形，
∴∠C＝60°，
∵AD⊥BC，
∴BD＝CD，
∴DE＝DC，
∴△CDE是等边三角形，
∴∠CDE＝60°．
【点睛】本题考查了直角三角形斜边上的中线，等边三角形的判定和性质，正确的识别图形是解题的关键．
能力提升
15．如图，已知△ABC中，∠ACB＝90°，CD为AB边上的高，∠ABC的平分线BE分别交CD、CA于点F、E，则下列结论正确的有（　　）
①∠CFE＝∠CEF；②∠FCB＝∠FBC，③∠A＝∠DCB；④∠CFE与∠CBF互余．
A．①③④ B．②③④ C．①②④ D．①②③
【思路点拨】①利用外角的性质可得∠1＝∠A+∠6，∠2＝∠4+∠5，由角平分线的性质可得：∠5＝∠6，由同角的余角相等可得：∠A＝∠4，进而可得∠1＝∠2，即∠CFE＝∠CEF；
②采用分析法，若∠FCB＝∠FBC，即∠4＝∠5，由（1）可知：∠A＝∠4，进而∠A＝∠5＝∠6，然后由直角三角形两锐角互余可得∠A＝30°，即只有当∠A＝30°时，∠FCB＝∠FBC而已知没有这个条件；
③由同角的余角相等可得：∠A＝∠4，即∠A＝∠DCB；
④由∠1＝∠2，∠1与∠5互余，可得∠2与∠5互余，即：∠CFE与∠CBF互余．
【解析】解：如图所示，
①∵BE平分∠ABC，
∴∠5＝∠6，
∵∠3+∠4＝90°，∠A+∠3＝90°，
∴∠A＝∠4，
∵∠1＝∠A+∠6，∠2＝∠4+∠5，
∠1＝∠2，
故∠CFE＝∠CEF，所以①正确；
②若∠FCB＝∠FBC，即∠4＝∠5，
由（1）可知：∠A＝∠4，
∴∠A＝∠5＝∠6，
∵∠A+∠5+∠6＝90°，
∴∠A＝30°，
即只有当∠A＝30°时，∠FCB＝∠FBC而已知没有这个条件，故②错误；
③∵∠3+∠4＝90°，∠A+∠3＝90°，
∴∠A＝∠4，
即∠A＝∠DCB，故③正确；
④∵∠1＝∠2，∠1+∠5＝90°，
∴∠2+∠5＝90°，
即：∠CFE与∠CBF互余，故④正确．
故选：A．
【点睛】本题考查了等腰三角形的判定，角平分线的定义，直角三角形两锐角互余的性质，同角的余角相等的性质，利用阿拉伯数字加弧线表示角更形象．
16．如图，在Rt△ABC中，已知，∠ACB＝90°，∠B＝15°，AB边的垂直平分线交AB于E，交BC于D，且BD＝13cm，则AC的长是（　　）
A．13cm B．6.5cm C．30cm D．6cm
【思路点拨】利用线段垂直平分线的性质得AD＝BD，利用等腰三角形的性质得∠DAE＝∠B＝15°且AD＝BD＝13cm，再利用外角的性质得∠ADC＝30°，解直角三角形即可得AC的值．
【解析】解；∵AB边的垂直平分线交AB于E，交BC于D（已知）
∴AD＝BD（线段垂直平分线的性质）
∴∠DAE＝∠B＝15°且AD＝BD＝13cm（等腰三角形的性质）
∴∠ADC＝30°（外角性质）
∴AC＝AD＝6.5cm．
故选：B．
【点睛】本题主要考查了线段垂直平分线的性质和含30°角的直角三角形的性质等知识；得到∠ADC＝30°是正确解答本题的关键．
17．如图，在△ABC中，∠C＝90°，点E是AC上的点，且∠1＝∠2，DE垂直平分AB，垂足是D，如果EC＝3cm，则AE等于（　　）
A．3cm B．4cm C．6cm D．9cm
【思路点拨】求出AE＝BE，推出∠A＝∠1＝∠2＝30°，求出DE＝CE＝3cm，根据含30度角的直角三角形性质求出即可．
【解析】解：∵DE垂直平分AB，
∴AE＝BE，
∴∠2＝∠A，
∵∠1＝∠2，
∴∠A＝∠1＝∠2，
∵∠C＝90°，
∴∠A＝∠1＝∠2＝30°，
∵∠1＝∠2，ED⊥AB，∠C＝90°，
∴CE＝DE＝3cm，
在Rt△ADE中，∠ADE＝90°，∠A＝30°，
∴AE＝2DE＝6cm，
故选：C．
【点睛】本题考查了垂直平分线性质，角平分线性质，等腰三角形性质，含30度角的直角三角形性质的应用，关键是求出∠A＝30°和得出DE的长．
18．如图，在△ABC中，∠CAB＝90°，边BC的垂直平分线交AC于点D，交BC于点E．若∠CBD＝2∠ABD，则∠C的度数为 　36°　．
【思路点拨】根据线段垂直平分线的性质得到DC＝DB，得到∠DBC＝∠C，根据题意得到∠ABD＝∠C，根据直角三角形的两锐角互余列式计算即可．
【解析】解：∵DE是BC的垂直平分线，
∴DC＝DB，
∴∠DBC＝∠C，
∵∠CBD＝2∠ABD，
∴∠ABD＝∠C，
∵∠CAB＝90°，
∴∠C+∠ABC＝90°，
∴∠C+∠C+∠C＝90°，
解得：∠C＝36°，
故答案为：36°．
【点睛】本题考查的是直角三角形的性质、线段垂直平分线的性质，熟记直角三角形的两锐角互余是解题的关键．
19．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，∠ACD＝3∠BCD，E是斜边AB的中点，∠ECD是　45　度．
【思路点拨】先求出∠BCD和∠ACD，再根据直角三角形两锐角互余求出∠B，根据直角三角形斜边上的中线等于斜边的一半可得CE＝BE，根据等边对等角可得∠BCE＝∠B，再求出∠ECD＝45°．
【解析】解：∵∠ACB＝90°，∠ACD＝3∠BCD，
∴∠BCD＝90°×＝22.5°，
∠ACD＝90°×＝67.5°，
∵CD⊥AB，
∴∠B＝90°﹣22.5°＝67.5°，
∵E是AB的中点，∠ACB＝90°，
∴CE＝BE，
∴∠BCE＝∠B＝67.5°，
∴∠ECD＝∠BCE﹣∠BCD＝67.5°﹣22.5°＝45°，
故答案为：45．
【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形的性质，熟记性质并准确识图，理清图中各角度之间的关系是解题的关键．
20．如图，在△ABC中，BA＝BC，∠ABC＝120°，BD⊥BC交AC于点D，BD＝，则AC的长 　3　．

【思路点拨】证明BD＝AD，CD＝2BD即可解决问题．
【解析】解：∵BA＝BC，∠ABC＝120°，
∴∠A＝∠C＝30°，
∵DB⊥BC，
∴∠DBC＝90°，
∴∠ABD＝∠ABC﹣∠DBC＝30°，
∴∠A＝∠ABD，
∴AD＝BD＝，
∵CD＝2BD＝2，
∴AC＝AD+DC＝+2＝3，
故答案为：3．
【点睛】本题考查直角三角形30度角的性质，解直角三角形等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
21．如图，已知∠AOB＝60°，点P在边OA上，OP＝16，点M、N在边OB上，PM＝PN，若MN＝4，则OM＝　6　．
【思路点拨】过点P作PD⊥OB，垂足为D，根据垂直定义可得∠PDO＝90°，再利用直角三角形的两个锐角互余可得∠OPD＝30°，然后利用含30度角的直角三角形的性质可得OD＝8，再利用等腰三角形的三线合一性质可得DM＝2，最后进行计算即可解答．
【解析】解：过点P作PD⊥OB，垂足为D，
∴∠PDO＝90°，
∵∠AOB＝60°，
∴∠OPD＝90°﹣∠AOB＝30°，
∵OP＝16，
∴OD＝OP＝8，
∵PM＝PN，PD⊥MN，
∴DM＝MN＝2，
∴OM＝OD﹣DM＝6，
故答案为：6．
【点睛】本题考查了等腰三角形的性质，含30度角的直角三角形，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
22．如图，在△ABC中，∠BAC＝90°，AD⊥BC于点D，BE平分∠ABC，AD、BE相交于点F．
（1）若∠CAD＝36°，求∠AEF的度数；
（2）试说明：∠AEF＝∠AFE．
【思路点拨】（1）根据同角的余角相等得到∠ABD＝∠CAD＝36°，根据角平分线的性质求出∠ABE，根据直角三角形的性质计算即可；
（2）根据角平分线的性质、直角三角形的性质证明结论．
【解析】（1）解：∵AD⊥BC，
∴∠ABD+∠BAD＝90°，
∵∠BAC＝90°，
∴∠BAD+∠CAD＝90°，
∴∠ABD＝∠CAD＝36°，
∵BE平分∠ABC，
∴∠ABE＝∠ABC＝18°，
∴∠AEF＝90°﹣∠ABE＝72°；
（2）证明：∵BE平分∠ABC，
∴∠ABE＝∠CBE，
∵∠ABE+∠AEF＝90°，∠CBE+∠BFD＝90°，
∴∠AEF＝∠BFD，
∵∠AFE＝∠BFD，
∴∠AEF＝∠AFE．
【点睛】本题考查的是直角三角形的性质，掌握直角三角形的两锐角互余是解题的关键．
23.已知：如图，在四边形ABCD中，∠BCD＝∠BAD＝90°，E，F分别是对角线BD，AC的中点．
（1）请判断线段EF与AC的位置关系，并说明理由；
（2）若∠ADC＝45°，请判断EF与AC的数量关系，并说明理由．
【思路点拨】（1）连接AE，EC，根据直角三角形斜边上的中线性质可得CE＝BD，AE＝BD，从而可得AE＝CE，然后利用等腰三角形的三线合一性质，即可解答；
（2）根据直角三角形斜边上的中线性质可得CE＝DE，AE＝DE，从而可得∠ECD＝∠CDE，∠EAD＝∠ADE，然后利用三角形的外角性质可得∠AEC＝2∠ADC＝90°，从而利用直角三角形斜边上的中线性质可得EF＝AC，即可解答．
【解析】解：（1）EF⊥AC，
理由：连接AE，EC，
∵∠BCD＝90°，点E是BD的中点，
∴CE＝BD，
∵∠BAD＝90°，点E是BD的中点，
∴AE＝BD，
∴AE＝CE，
∵点F是AC的中点，
∴EF⊥AC；
（2）EF＝AC，
理由：∵∠BCD＝90°，点E是BD的中点，
∴CE＝DE＝BD，
∴∠ECD＝∠CDE，
∵∠BAD＝90°，点E是BD的中点，
∴AE＝DE＝BD，
∴∠EAD＝∠ADE，
∵∠ADC＝45°，
∴∠AEC＝∠AEB+∠BEC
＝∠EAD+∠ADE+∠ECD+∠EDC
＝2∠ADE+2∠CDE
＝2（∠ADE+∠CDE）
＝2∠ADC
＝90°，
∵点F是AC的中点，
∴EF＝AC．
【点睛】本题考查了直角三角形斜边上的中线，等腰三角形的判定与性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
24.如图，一条船上午8时从海岛A出发，以20海里/时的速度向正北方向航行，上午10时到达海岛B处，分别从A，B处望灯塔C，测得∠NAC＝30°，∠NBC＝60°．
（1）求海岛B到灯塔C的距离；
（2）若这条船继续向正北航行，问上午几时小船与灯塔C的距离最短？
【思路点拨】（1）根据三角形的外角的性质，得∠ACB＝∠NBC﹣∠NAC＝30°，那么∠ACB＝∠NAC，故AB＝BC＝40 （海里）．
（2）如图，过点C作CP⊥AB于点P，根据垂线段最短，线段CP的长为小船与灯塔C的最短距离．欲确定什么时间小船与灯塔C的距离最短，求得AP．根据三角形内角和定理，得∠PCB＝180°﹣∠BPC﹣∠CBP＝30°．根据含30度角的直角三角形的性质，在Rt△CBP中，∠BCP＝30°，得PB＝BC＝20（海里），那么AP＝AB+BP＝40+20＝60（海里），从而解决此题．
【解析】解：（1）由题意得：AB＝20×2＝40（海里）．
∵∠NBC＝60°，∠NAC＝30°，
∴∠ACB＝∠NBC﹣∠NAC＝30°．
∴∠ACB＝∠NAC．
∴AB＝BC＝40 （海里）．
∴从海岛B到灯塔C的距离为40海里．
（2）如图，过点C作CP⊥AB于点P．
∴根据垂线段最短，线段CP的长为小船与灯塔C的最短距离，∠BPC＝90°．
又∵∠NBC＝60°，
∴∠PCB＝180°﹣∠BPC﹣∠CBP＝30°．
在Rt△CBP中，∠BCP＝30°，
∴PB＝BC＝20（海里），
∴AP＝AB+BP＝40+20＝60（海里）．
∴航行的时间为60÷20＝3（时）．
∴若这条船继续向正北航行，上午11时小船与灯塔C的距离最短．
【点睛】本题主要考查等腰三角形的判定、三角形外角的性质、含30°角的直角三角形的性质、垂线段最短，熟练掌握等腰三角形的判定、三角形外角的性质、含30°角的直角三角形的性质、垂线段最短是解决本题的关键．
培优拔尖
25.以下说法：
①如果三角形三个内角的比是1：2：3，那么这个三角形是直角三角形；
②如果三角形的一个外角等于与它相邻的内角，则这个三角形是直角三角形；
③如果一个三角形的三条高的交点恰好是三角形的一个顶点，那么这个三角形是直角三角形；
④如果∠A＝∠B＝∠C，那么△ABC是直角三角形；
⑤在△ABC中，若∠A+∠B＝∠C，则此三角形是直角三角形．其中说法正确的个数有（　　）
A．2个 B．3个 C．4个 D．5个
【思路点拨】根据三角形的内角和判断①④⑤，根据外角的定义判断②，根据直角三角形的三条高线交于直角顶点，判断③．
【解析】解：①如果三角形三个内角的比是1：2：3，则最大角的度数为：，那么这个三角形是直角三角形，说法正确，符合题意；
②如果三角形的一个外角等于与它相邻的内角，根据外角与它相邻的内角互补，得到这个内角是90°，那么这个三角形是直角三角形，说法正确，符合题意；
③如果一个三角形的三条高的交点恰好是三角形的一个顶点，那么这个三角形是直角三角形；说法正确，符合题意；
④如果，根据∠A+∠B+∠C＝2∠C＝180°，得到∠C＝90°，那么△ABC是直角三角形；说法正确，符合题意；
⑤在△ABC中，若∠A+∠B＝∠C，根据∠A+∠B+∠C＝2∠C＝180°，得到∠C＝90°，则此三角形是直角三角形．说法正确，符合题意；
综上：说法正确的个数有5个；
故选：D．
【点睛】本题考查三角形分类，三角形的内角和，三角形的外角的定义，三角形的高线．熟练掌握相关知识点，是解题的关键．
26．已知非Rt△ABC中，∠A＝60°，高BD和CE所在的直线相交于点H，求∠BHC的度数为（　　）
A．60° B．60°或150° C．120° D．60°或120°
【思路点拨】分情况讨论：①△ABC是锐角三角形，②△ABC是钝角三角形，分别根据直角三角形的性质和三角形内角和定理求解即可．
【解析】解：①△ABC是锐角三角形，如图1所示，
∵BD、CE是△ABC的高线，
∴∠ADB＝90°，∠BEC＝90°，
∵∠A＝60°，
∴∠ABD＝90°﹣60°＝30°，
∴∠BHC＝∠ABD+∠BEC＝30°+90°＝120°；
②△ABC是钝角三角形，如图2所示：
∵BD、CE是△ABC的高线，
∴∠AEC＝90°，∠ADB＝90°，
∴∠ADH＝90°，
∵∠ACE＝∠HCD，
∴∠BHC＝∠A＝60°．
综上所述，∠BHC的度数是120°或60°，
故选：D．
【点睛】本题考查了直角三角形的性质，三角形内角和定理，熟练掌握这些性质是解题的关键，注意分情况讨论．
27．如果等腰三角形一条边上的高等于这条边长的一半，那么这个等腰三角形的顶角的度数是 　30°或90°或150°　．
【思路点拨】三种情形①BD是腰上的高．②AD是底边上的高，分别求解即可．③△ABC是钝角三角形．
【解析】解：①如图1中，
∵AB＝AC，BD⊥AC，
BD＝AC＝AB，
∴sinA＝，
∴∠A＝30°；
②如图2中，
∵AB＝AC，AD⊥BC，
∴BD＝CD，
∵AD＝BC，
∴AD＝DB＝DC，
∴∠DAB＝∠DAC＝45°，
∴∠BAC＝90°；
③如图，AB＝AC，BD⊥AC，BD＝AB，
则∠BAD＝30°，∠BAC＝150°，
∴等腰三角形的顶角为30°或90°或150°．
故答案为：30°或90°或150°．
【点睛】本题考查等腰三角形的性质、等腰三角形的判定和性质、锐角三角函数等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．
28．如图，已知锐角△ABC中，CD、BE分别是AB、AC边上的高，M、N分别是线段BC、DE的中点．
（1）求证：MN⊥DE；
（2）若∠ABC＝70°，∠ACB＝50°，连结DM、ME，求∠DME的度数；
（3）猜想∠DME与∠A之间的关系，并证明你的猜想．
【思路点拨】（1）连接DM，ME，根据直角三角形的性质得到DM＝BC，ME＝BC，得到DM＝ME，根据等腰直角三角形的性质证明；
（2）根据三角形内角和定理、等腰三角形性质、平角的定义求解即可；
（3）根据三角形内角和定理、等腰三角形的性质求解即可．
【解析】（1）证明：如图，连接DM，ME，
∵CD、BE分别是AB、AC边上的高，M是BC的中点，
∴DM＝BC，ME＝BC，
∴DM＝ME，
又∵N为DE中点，
∴MN⊥DE；
（2）解：在△ABC中，∠ABC+∠ACB＝180°﹣∠A，
∵∠ABC＝70°，∠ACB＝50°，
∴180°﹣∠A＝120°，
∵DM＝ME＝BM＝MC，
∴∠BMD+∠CME＝（180°﹣2∠ABC）+（180°﹣2∠ACB）＝360°﹣2（∠ABC+∠ACB）＝120°，
∴∠DME＝180°﹣（∠BMD+∠CME）＝60°；
（3）解：∠DME＝180°﹣2∠A，理由如下：
在△ABC中，∠ABC+∠ACB＝180°﹣∠A，
∵DM＝ME＝BM＝MC，
∴∠BMD+∠CME＝（180°﹣2∠ABC）+（180°﹣2∠ACB）
＝360°﹣2（∠ABC+∠ACB）
＝360°﹣2（180°﹣∠A）
＝2∠A，
∴∠DME＝180°﹣2∠A．
【点睛】此题考查了直角三角形斜边上的中线、等腰三角形的判定与性质，熟记直角三角形斜边上的中线、等腰三角形的判定与性质是解题的关键．
29.如图，在△ABC中，AB＝AC，∠BAC＝120°，AD是BC边上的中线，且BD＝BE，CD的垂直平分线MF交AC于F，交BC于M，MF的长为2．
（1）求∠ADE的度数；
（2）△ADF是正三角形吗？为什么？
（3）求AB的长．
【思路点拨】（1）根据等腰三角形的性质和三角形内角和定理求出∠B和∠C，求出∠BDE，即可求出答案；
（2）求出DF＝CF，根据等腰三角形的性质求出∠FDC＝∠C，求出∠AFD和∠DAF，根据等边三角形的判定得出即可；
（3）求出CF和DF，根据等边三角形的性质求出AF，求出AC，即可求出AB．
【解析】解：（1）∵在△ABC中，AB＝AC，∠BAC＝120°，
∴∠B＝∠C＝×（180°﹣∠BAC）＝30°，
∵BD＝BE，
∴∠BDE＝∠BED＝×（180°﹣∠B）＝75°，
∵在△ABC中，AB＝AC，AD是BC边上的中线，
∴AD⊥BC，
∴∠ADB＝90°，
∴∠ADE＝∠ADB﹣∠BDE＝15°；
（2）△ADF是正三角形，
理由是：∵CD的垂直平分线MF交AC于F，交BC于M，
∴DF＝CF，
∵∠C＝30°，
∴∠FDC＝∠C＝30°，
∴∠AFD＝∠C+∠FDC＝60°，
∵AD⊥BC，
∴∠ADC＝90°，
∴∠DAF＝90°﹣∠C＝60°，
∴∠ADF＝60°，
即∠FAD＝∠ADF＝∠AFD＝60°，
∴△ADF是正三角形；
（3）∵CD的垂直平分线MF，
∴∠FMC＝90°，
∵∠C＝30°，MF＝2，
∴FC＝2MF＝4，
∵DF＝FC，
∴DF＝4，
∵△ADF是等边三角形，
∴AF＝DF＝4，
∴AC＝AF+CF＝4+4＝8，
∵AB＝AC，
∴AB＝8．
【点睛】本题考查了线段垂直平分线性质，等边三角形的性质和判定，含30°角的直角三角形的性质，等腰三角形的性质等知识点，能综合运用定理进行推理是解此题的关键．
30．如图，△ABC是边长为4的等边三角形，点P在AB上，过点P作PE⊥AC，垂足为E，延长BC到点Q，使CQ＝PA，连接PQ交AC于点D，求DE的长．
【思路点拨】过P点作PN∥BC交AC于点N，证明△PNA是等边三角形，再证明△PND≌△QCD（AAS），通过等量代换可得DE＝AE+CD＝EN+ND＝CA＝2．
【解析】解：过P点作PN∥BC交AC于点N，
∴∠APN＝∠B，
∵△ABC是等边三角形，
∴∠APN＝∠PAN＝60°，
∴△PNA是等边三角形，
∴AP＝PN，
∵AP＝CQ，
∴PN＝CQ，
∵PN∥CQ，
∴∠Q＝∠NPD，
∴△PND≌△QCD（AAS），
∴ND＝CD，
∵PE⊥AN，
∴AE＝EN，
∴AE+CD＝EN+ND＝CA，
∵AC＝4，
∴DE＝2．
【点睛】本题考查等边三角形的性质，熟练掌握等边三角形的性质，平行线的性质，三角形全等的判定及性质是解题的关键．
31.如图，在△ABC中，∠C＝90°，∠A＝30°，AB＝4cm，动点P、Q同时从A、B两点出发，分别在AB、BC边上匀速移动，它们的速度分别为VP＝2cm/s，VQ＝1cm/s，当点P到达点B时，P、Q两点同时停止运动，设点P的运动时间为ts．
（1）当t为何值时，△PBQ为等边三角形？
（2）当t为何值时，△PBQ为直角三角形？
【思路点拨】用含t的代数式表示出BP、BQ．
（1）由于∠B＝60°，当BP＝BQ时，可得到关于t的一次方程，求解即得结论；
（2）分两种情况进行讨论：当∠BQP＝90°时，当∠BPQ＝90°时．利用直角三角形中，含30°角的边间关系，得到关于t的一次方程，求解得结论．
【解析】解：在△ABC中，∵∠C＝90°，∠A＝30°，
∴∠B＝60°．
∵4÷2＝2，
∴0≤t≤2，BP＝4﹣2t，BQ＝t.
（1）当BP＝BQ时，△PBQ为等边三角形．
即4﹣2t＝t．
∴．
当时，△PBQ为等边三角形；
（2）若△PBQ为直角三角形，
①当∠BQP＝90°时，BP＝2BQ，
即4﹣2t＝2t，
∴t＝1．
②当∠BPQ＝90°时，BQ＝2BP，
即t＝2（4﹣2t），
∴．
即当或t＝1时，△PBQ为直角三角形．
【点睛】本题考查了含30°角的直角三角形、等边三角形以及分类讨论的思想方法，利用“直角三角形中，30°角所对的边等于斜边的一半”及“有一个角是60°的等腰三角形是等边三角形”，得到关于t的一次方程是解决本题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)