浙教版数学八年级上册 1.3证明 第2课时 三角形内角和定理及推论课件(共32张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 1.3证明 第2课时 三角形内角和定理及推论课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 736.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 15:05:19 | ||
图片预览










文档简介
(共32张PPT)
第1章 三角形的初步知识
1.3 证明
第2课时 三角形内角和定理及推论
证明三角形内角和定理,掌握它的推论,并能运用这些定理解决简单的问题;
经历探索与证明的过程,进一步发展推理论证能力;
学习目标
在一题多解、一题多变中,积累解决几何问题的经验,提升解决问题的能力.
我们知道三角形三个内角的和等于180°.你还记得这个结论的探索过程吗?
命题:三角形的内角和是180°.
探究一
实验1:如下图,先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图2),然后把另处两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果。
A
C
B
B
A
C
图2
图1
BA
BAC
图3
图4
C
这只是实验得出的结论,不能当作定理,只有经过严格的几何证明,得出命题的正确性,才能作为几何定理,今后,在几何里,常采用这种方法得到新知识.
A
B
C
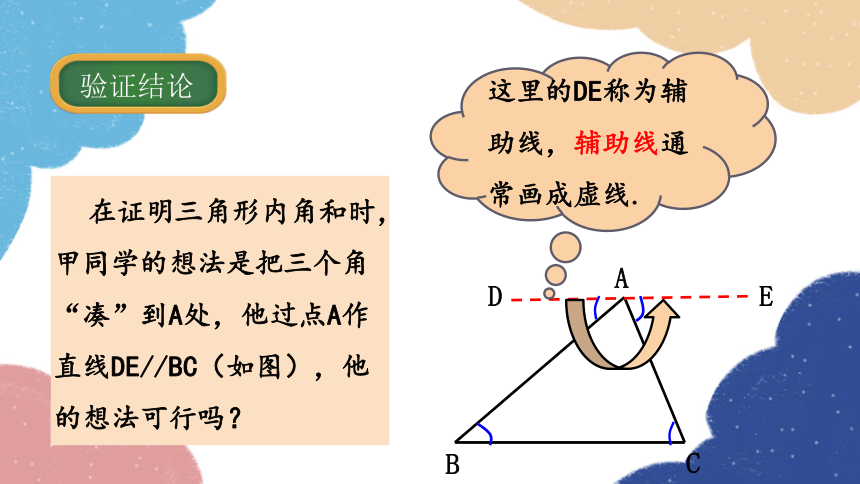
在证明三角形内角和时,甲同学的想法是把三个角“凑”到A处,他过点A作直线DE//BC(如图),他的想法可行吗?
D
E
这里的DE称为辅助线,辅助线通常画成虚线.
验证结论
证明:过点A作DE∥BC,
则∠C=∠CAE,∠B=∠BAD(两直线平行,内错角相等),
∴∠BAC+∠B+∠C
=∠BAC+∠BAD+∠CAE =∠DAE=180 (平角的定义).
作辅助线
还有没有其他的添线方法呢?
实验2: 将纸片三角形顶角剪下,随意将它们拼凑在一起.
3
2
2
这种方法可以通过怎样在原三角形中添线证明?
2
D
B
C
A
1
E
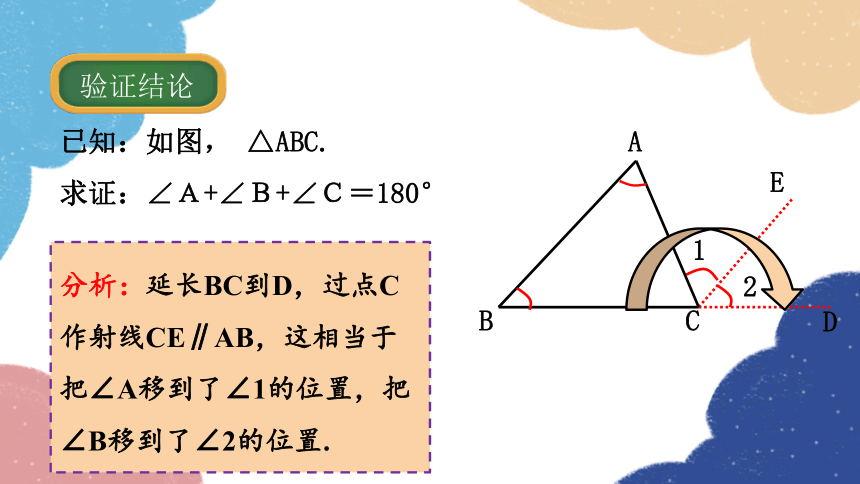
已知:如图, △ABC.
求证:∠A+∠B+∠C=180°
分析:延长BC到D,过点C作射线CE∥AB,这相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
验证结论
证明: 作BC的延长线CD,过点C作射线CE//AB,
则∠1=∠A(两直线平行,内错角相等),
∠2=∠B(两直线平行,同位角相等),
∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°(等量代换).
作辅助线
三角形内角和定理 三角形的内角和等于180°.
这两种添线依据都是通过平行线的性质,利用内错角或同位角将三角形三个内角转化为一个平角进行证明的,你还有别的方法吗?
B
C
A
1
E
这样添线的依据是什么?尝试证明.
方法总结
证明几何命题的格式
(1)按题意画出图形;
(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;
(3)在“证明”中写出推理过程.
巩固练习
证明命题“两条平行直线被第三条直线所截,同位角的平分线互相平行”是真命题.
已知:如图,直线AB∥CD,直线EF分别交AB、CD于点E、F,EH、FG分别平分∠BEI、∠DFE.
求证:EH∥FG.
A
B
C
D
E
F
G
H
I
1
2
证明:∵直线AB∥CD(已知),
∴ ∠BEI=∠DFE(两直线平行,同位角相等),
又∵ EH、FG分别平分∠BEI、∠DFE,
∴∠1= ∠BEI,∠2= ∠DFE(角平分线的定义),
∴∠1=∠2(等量代换),
∴EH∥FG(同位角相等,两直线平行).
A
B
C
D
E
F
G
H
I
1
2
练习1、如图,△ABC中,∠A=60°,∠B∶∠C=1:5,则∠B=___.
分析:在△ABC中,
∠A+∠B+∠C=180°(三角形的内角和定理),
∴ ∠B+∠C=180°-∠A=120°,
又∵ ∠B∶∠C=1:5,∴∠B=20°.
B
C
A
巩固练习
20°
练习2、如图,在△ABC中,∠B=50°, ∠C=60°,点D是BC边上的任意一点,DE⊥AB于E,DF⊥AC于F,那么∠EDF=____.
解:在△ABC中,
∠A+∠B+∠C=180°(三角形的内角和定理),
∴∠A=180°-∠B-∠C =70°,
又∵ DE⊥AB于E,DF⊥AC于F,
∴∠AED=∠DFA=90°,∴ ∠EDF=110°.
110°
B
A
C
1
1
1
A
B
C
探究二
A
B
C
观察∠1在各图中的位置,它们有什么共同特征?
1、∠1的顶点在三角形的一个顶点上;
2、∠1和三角形共用一条边;
3、∠1的另一条边是三角形的某条边的延长线.
.
.
.
△ABC内角的一条边与另一条边的反向延长线组成的角,称为△ABC的外角.如右图,∠1是△ABC的∠ABC的外角.
∠1与其他角有什么关系?能证明你的结论吗?
4
2
3
B
C
A
1
D
外角的定义
分析:如图,∠1+∠4=180°(平角的定义), ∠2+∠3+∠4=180°(三角形内角和定理),
∴∠1=∠2+∠3(等量代换).
定理 三角形的外角等于与它不相邻的两个内角的和.
4
2
3
B
C
A
1
D
例题讲解
例 已知:如图,∠B+∠D= ∠BCD.求证:AB∥DE.
分析:如图,延长BC,交DE于点F.根据平行线的判定定理,只要证明∠B=∠CFD,或∠B+∠BFE=180°,就能证明AB∥DE.
A
B
D
E
C
F
证明:如图,延长BC,交DE于点F.
∵ ∠B+∠D= ∠BCD(已知),
又∵ ∠BCD=∠D+∠CFD(三角形的外角等于与它不相邻的两个内角的和),
∴ ∠B+∠D=∠D+∠CFD,
∴ ∠B=∠CFD,
∴AB∥DE(内错角相等,两直线平行).
A
B
D
E
C
F
方法总结
关于辅助线
(1)辅助线是为了证明需要在原图上添画的线;
(2)添加辅助线的过程需要写入证明中,通常画成虚线;
(3)添加辅助线,可构造新图形,其作用是把分散的条件集中,把隐含条件凸显出来,起牵线搭桥的作用.
1、已知,如图,AD是△ABC的高.
求证:∠B+∠BAD=∠C+∠CAD.
B
C
A
D
分析:如图,根据三角形的外角等于与它不相邻的两个内角的和定理,得出∠ADC=∠B+∠BAD,∠ADB=∠C+∠CAD,题目即可得证明.
课内练习
证明:由题意可得,
∠ADC= ∠B+∠BAD,∠ADB=∠C+∠CAD(三角形的外角等于与它不相邻的两个内角的和),
又∵ AD是△ABC的高,
∴ ∠ADC=∠ADB=90°,
∴∠B+∠BAD=∠C+∠CAD.(等量代换)
2、星期天,小明见爸爸愁眉苦脸地在看一张图纸,他便悄悄地来到爸爸身边,想看爸爸为什么犯愁.爸爸见到他,高兴地对他说:“来帮我一个忙,你看这是一个四边形零件的平面图,它要求∠BDC等于140°才算合格.”小明通过测量得∠A=90°,∠B=19°,∠C=40°后就下结论说此零件不合格.于是爸爸让小明解释这是为什么?
小明很轻松地说出了原因,并用如下的两种方法解出此题.请你代小明分别说出不合格的理由.
①如图(1),连结AD并延长;②如图(2),延长CD交AB于E.
分析:直接利用各个三角形中的外角和等于与它不相邻的两个内角和求解.
解:(1)∠BDC=∠1+∠2=∠A+∠B+∠C=90°+19°+40°=149°≠140°,故不合格;
(2)∠BDC=∠1+∠B=∠A+∠C+∠B=149°≠140°,故不合格.
(1)三角形的外角等于与它不相邻的两个内角和.
(2)三角形的内角和是180°.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.
规律总结
3、证明命题“三角形不共顶点的三个外角的和等于360°”是真命题.
已知:如图,△ABC的三个内角分别为∠1、 ∠2、 ∠3,相对应的外角为∠4、 ∠5、 ∠6.
求证: ∠4+∠5+∠6=360°.
B
C
A
1
2
3
4
5
6
证明:∵ ∠1、 ∠2、 ∠3是△ABC的三个内角,
∴ ∠1+∠2+∠3=180°(三角形内角和定理),
又∵∠4=∠2+∠3,∠5=∠1+∠3,∠6=∠1+∠2(三角形的外角等于与它不相邻的两个内角的和),
∴∠4+∠5+∠6
=2(∠1+∠2+∠3)
=2×180°=360°.
B
C
A
1
2
3
4
5
6
1、三角形内角和定理的证明,证明思想是运用辅助线将原三角形处于不同位置的三个内角集中在一起,拼成一个平角.辅助线是联系命题的条件和结论的桥梁,今后我们还要学习它.
2、三角形的外角性质,是由三角形的内角和定理直接推理得到的一个推论.
课堂小结
感谢观看!
第1章 三角形的初步知识
1.3 证明
第2课时 三角形内角和定理及推论
证明三角形内角和定理,掌握它的推论,并能运用这些定理解决简单的问题;
经历探索与证明的过程,进一步发展推理论证能力;
学习目标
在一题多解、一题多变中,积累解决几何问题的经验,提升解决问题的能力.
我们知道三角形三个内角的和等于180°.你还记得这个结论的探索过程吗?
命题:三角形的内角和是180°.
探究一
实验1:如下图,先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图2),然后把另处两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果。
A
C
B
B
A
C
图2
图1
BA
BAC
图3
图4
C
这只是实验得出的结论,不能当作定理,只有经过严格的几何证明,得出命题的正确性,才能作为几何定理,今后,在几何里,常采用这种方法得到新知识.
A
B
C
在证明三角形内角和时,甲同学的想法是把三个角“凑”到A处,他过点A作直线DE//BC(如图),他的想法可行吗?
D
E
这里的DE称为辅助线,辅助线通常画成虚线.
验证结论
证明:过点A作DE∥BC,
则∠C=∠CAE,∠B=∠BAD(两直线平行,内错角相等),
∴∠BAC+∠B+∠C
=∠BAC+∠BAD+∠CAE =∠DAE=180 (平角的定义).
作辅助线
还有没有其他的添线方法呢?
实验2: 将纸片三角形顶角剪下,随意将它们拼凑在一起.
3
2
2
这种方法可以通过怎样在原三角形中添线证明?
2
D
B
C
A
1
E
已知:如图, △ABC.
求证:∠A+∠B+∠C=180°
分析:延长BC到D,过点C作射线CE∥AB,这相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
验证结论
证明: 作BC的延长线CD,过点C作射线CE//AB,
则∠1=∠A(两直线平行,内错角相等),
∠2=∠B(两直线平行,同位角相等),
∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°(等量代换).
作辅助线
三角形内角和定理 三角形的内角和等于180°.
这两种添线依据都是通过平行线的性质,利用内错角或同位角将三角形三个内角转化为一个平角进行证明的,你还有别的方法吗?
B
C
A
1
E
这样添线的依据是什么?尝试证明.
方法总结
证明几何命题的格式
(1)按题意画出图形;
(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;
(3)在“证明”中写出推理过程.
巩固练习
证明命题“两条平行直线被第三条直线所截,同位角的平分线互相平行”是真命题.
已知:如图,直线AB∥CD,直线EF分别交AB、CD于点E、F,EH、FG分别平分∠BEI、∠DFE.
求证:EH∥FG.
A
B
C
D
E
F
G
H
I
1
2
证明:∵直线AB∥CD(已知),
∴ ∠BEI=∠DFE(两直线平行,同位角相等),
又∵ EH、FG分别平分∠BEI、∠DFE,
∴∠1= ∠BEI,∠2= ∠DFE(角平分线的定义),
∴∠1=∠2(等量代换),
∴EH∥FG(同位角相等,两直线平行).
A
B
C
D
E
F
G
H
I
1
2
练习1、如图,△ABC中,∠A=60°,∠B∶∠C=1:5,则∠B=___.
分析:在△ABC中,
∠A+∠B+∠C=180°(三角形的内角和定理),
∴ ∠B+∠C=180°-∠A=120°,
又∵ ∠B∶∠C=1:5,∴∠B=20°.
B
C
A
巩固练习
20°
练习2、如图,在△ABC中,∠B=50°, ∠C=60°,点D是BC边上的任意一点,DE⊥AB于E,DF⊥AC于F,那么∠EDF=____.
解:在△ABC中,
∠A+∠B+∠C=180°(三角形的内角和定理),
∴∠A=180°-∠B-∠C =70°,
又∵ DE⊥AB于E,DF⊥AC于F,
∴∠AED=∠DFA=90°,∴ ∠EDF=110°.
110°
B
A
C
1
1
1
A
B
C
探究二
A
B
C
观察∠1在各图中的位置,它们有什么共同特征?
1、∠1的顶点在三角形的一个顶点上;
2、∠1和三角形共用一条边;
3、∠1的另一条边是三角形的某条边的延长线.
.
.
.
△ABC内角的一条边与另一条边的反向延长线组成的角,称为△ABC的外角.如右图,∠1是△ABC的∠ABC的外角.
∠1与其他角有什么关系?能证明你的结论吗?
4
2
3
B
C
A
1
D
外角的定义
分析:如图,∠1+∠4=180°(平角的定义), ∠2+∠3+∠4=180°(三角形内角和定理),
∴∠1=∠2+∠3(等量代换).
定理 三角形的外角等于与它不相邻的两个内角的和.
4
2
3
B
C
A
1
D
例题讲解
例 已知:如图,∠B+∠D= ∠BCD.求证:AB∥DE.
分析:如图,延长BC,交DE于点F.根据平行线的判定定理,只要证明∠B=∠CFD,或∠B+∠BFE=180°,就能证明AB∥DE.
A
B
D
E
C
F
证明:如图,延长BC,交DE于点F.
∵ ∠B+∠D= ∠BCD(已知),
又∵ ∠BCD=∠D+∠CFD(三角形的外角等于与它不相邻的两个内角的和),
∴ ∠B+∠D=∠D+∠CFD,
∴ ∠B=∠CFD,
∴AB∥DE(内错角相等,两直线平行).
A
B
D
E
C
F
方法总结
关于辅助线
(1)辅助线是为了证明需要在原图上添画的线;
(2)添加辅助线的过程需要写入证明中,通常画成虚线;
(3)添加辅助线,可构造新图形,其作用是把分散的条件集中,把隐含条件凸显出来,起牵线搭桥的作用.
1、已知,如图,AD是△ABC的高.
求证:∠B+∠BAD=∠C+∠CAD.
B
C
A
D
分析:如图,根据三角形的外角等于与它不相邻的两个内角的和定理,得出∠ADC=∠B+∠BAD,∠ADB=∠C+∠CAD,题目即可得证明.
课内练习
证明:由题意可得,
∠ADC= ∠B+∠BAD,∠ADB=∠C+∠CAD(三角形的外角等于与它不相邻的两个内角的和),
又∵ AD是△ABC的高,
∴ ∠ADC=∠ADB=90°,
∴∠B+∠BAD=∠C+∠CAD.(等量代换)
2、星期天,小明见爸爸愁眉苦脸地在看一张图纸,他便悄悄地来到爸爸身边,想看爸爸为什么犯愁.爸爸见到他,高兴地对他说:“来帮我一个忙,你看这是一个四边形零件的平面图,它要求∠BDC等于140°才算合格.”小明通过测量得∠A=90°,∠B=19°,∠C=40°后就下结论说此零件不合格.于是爸爸让小明解释这是为什么?
小明很轻松地说出了原因,并用如下的两种方法解出此题.请你代小明分别说出不合格的理由.
①如图(1),连结AD并延长;②如图(2),延长CD交AB于E.
分析:直接利用各个三角形中的外角和等于与它不相邻的两个内角和求解.
解:(1)∠BDC=∠1+∠2=∠A+∠B+∠C=90°+19°+40°=149°≠140°,故不合格;
(2)∠BDC=∠1+∠B=∠A+∠C+∠B=149°≠140°,故不合格.
(1)三角形的外角等于与它不相邻的两个内角和.
(2)三角形的内角和是180°.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.
规律总结
3、证明命题“三角形不共顶点的三个外角的和等于360°”是真命题.
已知:如图,△ABC的三个内角分别为∠1、 ∠2、 ∠3,相对应的外角为∠4、 ∠5、 ∠6.
求证: ∠4+∠5+∠6=360°.
B
C
A
1
2
3
4
5
6
证明:∵ ∠1、 ∠2、 ∠3是△ABC的三个内角,
∴ ∠1+∠2+∠3=180°(三角形内角和定理),
又∵∠4=∠2+∠3,∠5=∠1+∠3,∠6=∠1+∠2(三角形的外角等于与它不相邻的两个内角的和),
∴∠4+∠5+∠6
=2(∠1+∠2+∠3)
=2×180°=360°.
B
C
A
1
2
3
4
5
6
1、三角形内角和定理的证明,证明思想是运用辅助线将原三角形处于不同位置的三个内角集中在一起,拼成一个平角.辅助线是联系命题的条件和结论的桥梁,今后我们还要学习它.
2、三角形的外角性质,是由三角形的内角和定理直接推理得到的一个推论.
课堂小结
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
