3. 6 圆内接四边形 课件(共25张PPT)
文档属性
| 名称 | 3. 6 圆内接四边形 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
浙教版九年级上册
3.6 圆内接四边形
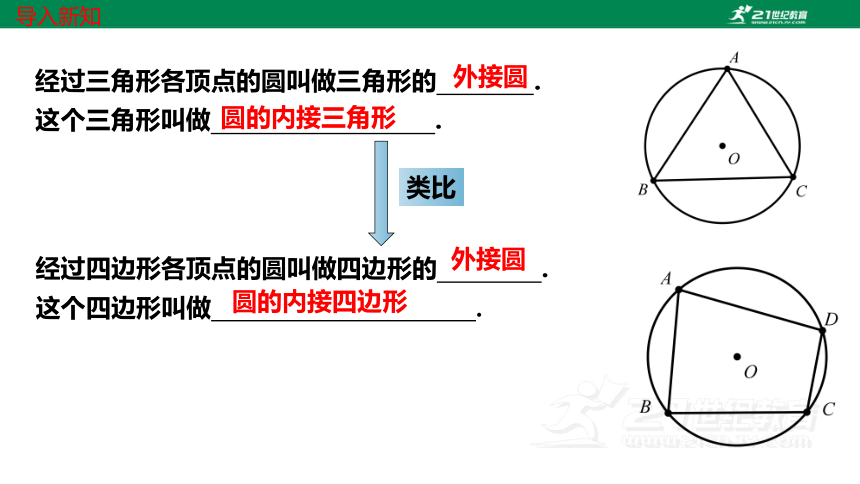
经过三角形各顶点的圆叫做三角形的 .
这个三角形叫做 .
外接圆
圆的内接三角形
类比
经过四边形各顶点的圆叫做四边形的 .
这个四边形叫做 .
外接圆
圆的内接四边形
导入新知
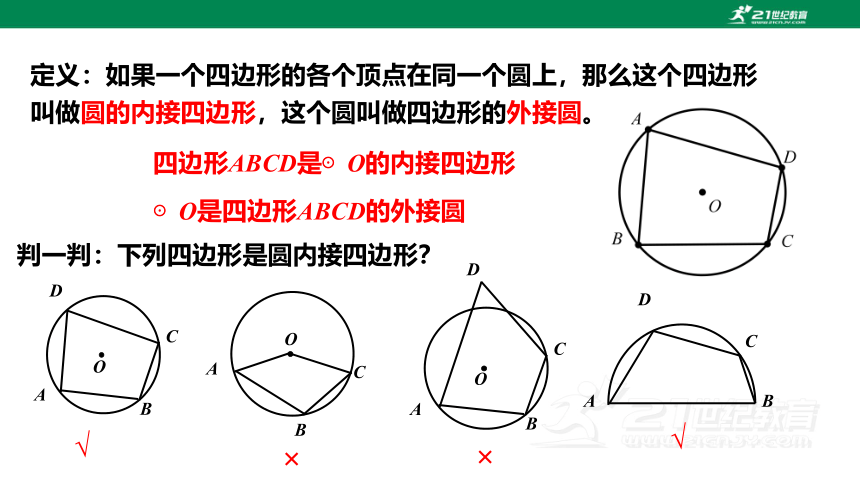
定义:如果一个四边形的各个顶点在同一个圆上,那么这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆。
四边形ABCD是⊙O的内接四边形
⊙O是四边形ABCD的外接圆
判一判:下列四边形是圆内接四边形?
A
O
B
C
D
A
O
B
C
A
O
B
C
D
A
B
C
D
√
×
×
√
探究:四边形ABCD内接于⊙o,猜想它的对角∠A、∠C之间有什么数量关系?
1.特殊情况:若BD为直径
BD为直径
∠A=∠C=90
∠A+∠C=180
∠ADC+∠ABC=180
2.一般化:若BD不为直径,上面的结论还成立吗?
┓
┓
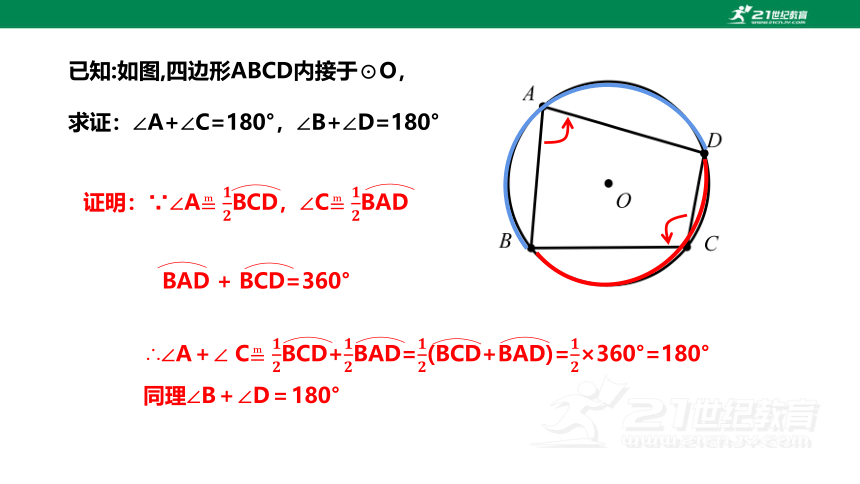
已知:如图,四边形ABCD内接于⊙O,
求证:∠A+∠C=180°,∠B+∠D=180°
证明:∵∠ABCD,∠CBAD
BAD + BCD=360°
∴∠A+∠ C BCD+BAD=(BCD+BAD)=×360°=180°
同理∠B+∠D=180°
几何语言:
∵四边形ABCD内接于⊙O
∴∠A+∠C=180
∠B+∠D=180
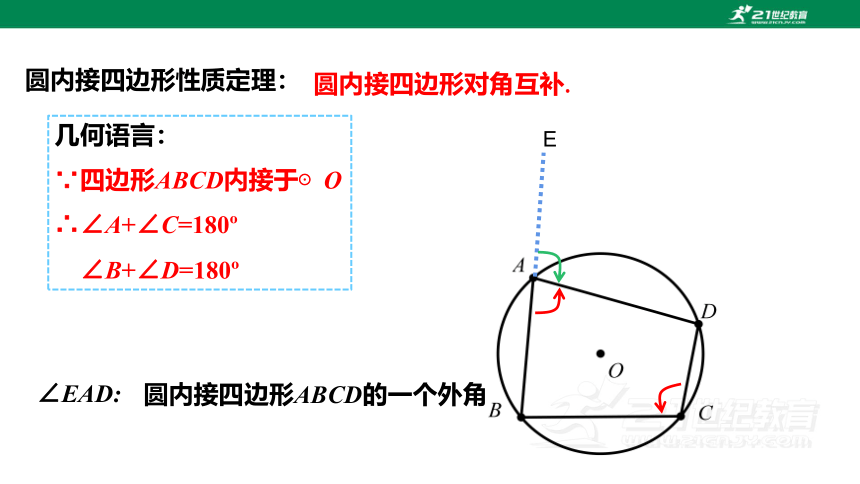
圆内接四边形性质定理:
圆内接四边形对角互补.
E
∠EAD:
圆内接四边形ABCD的一个外角
如图,若∠EAD是圆内接四边形ABCD的一个外角,
证明:
∠EAD=∠C
∠C + ∠BAD=180
∠EAD+∠BAD=180
推论:圆内接四边形的一个外角等于它的内对角.
几何语言
∵∠EAD是圆内接四边形ABCD的外角
∴∠EAD=∠C
求证:∠EAD=∠C
例1: 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D, 求证:DB=DC
证明:∵AD是∠EAC的平分线 ∴∠1=∠2
∵四边形ABCD内接于圆O
∴∠DCB=∠1
而∠2=∠DBC
∴∠DCB=∠DBC
∴DB=DC
(圆内接四边形的一个外角等于它的内对角).
★
★
▲
▲
新知讲解
例2 如果要把横截面直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能地大,应怎样锯?如果这根原木长15m,问锯出的木材的体积为多少立方米(树皮等损耗略去不计)?
思考:要使锯出的横截面正方形的面积尽可能大,正方形和圆
的应该满足什么关系?
正方形内接于⊙O
问题:如何画出这个正方形?
解:当原木的直径为30cm时,
∴正方形ABCD的面积为:
∴木材的体积为:4.5×10-2×15=0.675(m3).
AO=BO=15cm,
┓
A
B
C
D
圆内接四边形的外角等于内对角
圆内接四边形对角互补
一般
特殊
┓
┓
知识小结
1.四边形ABCD内接于⊙O,则∠A+∠C=______
∠B+∠ADC=_______;
若∠B=80°,
则∠ADC=______ ,
∠CDE=_________.
E
D
B
A
C
180°
180°
100°
80°
夯实基础,稳扎稳打
2.如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BAD= ,∠BCD= .
50°
130°
3.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE 的大小是( )
A.115° B.l05° C.100° D.95°
B
4、如图,点A,B,C,D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径的长是____ .
5、如图,四边形ABCD为圆的内接四边形,DA,CB的延长线交于点P,∠P=30°,∠ABC=100°,则∠C= 。
70°
.
6.如图,四边形ABCD内接于⊙O
∠A=∠C,∠B=∠D,那么四边形ABCD是怎样的特殊四边形?
∠A=∠C=∠B=∠D=900
四边形ABCD是矩形
7.若ABCD为圆内接四边形,则下列哪个选项可能成立( )
(A)∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4
(B)∠A∶∠B∶∠C∶∠D = 2∶1∶3∶4
(C)∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4
(D)∠A∶∠B∶∠C∶∠D = 4∶3∶2∶1
B
8. 在圆内接四边形ABCD中, ∠A,∠B,∠C的度数之比是2︰3︰7.求这个四边形各角的度数.
解:设∠A,∠B,∠C的度数分别对于2x,3x,7x,
∵四边形ABCD内接于圆,
∴ ∠A+ ∠C=∠B+∠D=180°,
∵2x+7x=180°,
∴ x=20°.
∴ ∠A=40°, ∠B=60°, ∠C =140°,
∠D=180°-60°=120°.
9.已知:如图,以等腰三角形ABC的底边BC为直径的☉O分别交两腰AB,AC于点D,E,连结DE.求证:DE∥BC.
证明:∵四边形BDCE是圆O的内接四边形 ∴∠ADE=∠C
∵AB=AC
∴∠B=∠C
∴∠ADE=∠B
∴DE∥BC.
连续递推,豁然开朗
10.在圆内接四边形ABCD中, 的度数之比为
1:2∶3∶4.求四边形ABCD各内角的度数.
A
B
C
D
3600×
=
︵
AC
m
=
︵
BC
m
3600×
=
︵
CD
m
3600×
=
︵
AD
m
3600×
∴ ∠A=90°, ∠B=126°,
∠C =90°,∠D=54°
连续递推,豁然开朗
.
11.已知四边形ABCD的内角∠A, ∠ B, ∠ C, ∠ D的度数之比为3:1:2:5,判断这个四边形是不是圆内接四边形,并说明理由.
3+2≠1+5
四边形是不是圆内接四边形
12.在圆内接四边形ABCD中,已知∠A=50° ∠D- ∠ B=40°.求∠ B, ∠ C, ∠ D的度数.
∠C=180°-∠A=180°-50°=1300
.
.
圆内接平行四边形一定是矩形
A
B
C
D
︵
CD
=
︵
AB
∴
∵AD=BC
︵
BC
=
︵
AD
∴
∵AB=CD
分析:
∴∠ABCD
=900
13.证明:圆内接平行四边形一定是矩形
14、如图 ,⊙O是正方形 ABCD的外接圆,点 P 在⊙O上,则∠APB等于( )
A 30° B 45° C 55° D 60°
B
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
3.6 圆内接四边形
经过三角形各顶点的圆叫做三角形的 .
这个三角形叫做 .
外接圆
圆的内接三角形
类比
经过四边形各顶点的圆叫做四边形的 .
这个四边形叫做 .
外接圆
圆的内接四边形
导入新知
定义:如果一个四边形的各个顶点在同一个圆上,那么这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆。
四边形ABCD是⊙O的内接四边形
⊙O是四边形ABCD的外接圆
判一判:下列四边形是圆内接四边形?
A
O
B
C
D
A
O
B
C
A
O
B
C
D
A
B
C
D
√
×
×
√
探究:四边形ABCD内接于⊙o,猜想它的对角∠A、∠C之间有什么数量关系?
1.特殊情况:若BD为直径
BD为直径
∠A=∠C=90
∠A+∠C=180
∠ADC+∠ABC=180
2.一般化:若BD不为直径,上面的结论还成立吗?
┓
┓
已知:如图,四边形ABCD内接于⊙O,
求证:∠A+∠C=180°,∠B+∠D=180°
证明:∵∠ABCD,∠CBAD
BAD + BCD=360°
∴∠A+∠ C BCD+BAD=(BCD+BAD)=×360°=180°
同理∠B+∠D=180°
几何语言:
∵四边形ABCD内接于⊙O
∴∠A+∠C=180
∠B+∠D=180
圆内接四边形性质定理:
圆内接四边形对角互补.
E
∠EAD:
圆内接四边形ABCD的一个外角
如图,若∠EAD是圆内接四边形ABCD的一个外角,
证明:
∠EAD=∠C
∠C + ∠BAD=180
∠EAD+∠BAD=180
推论:圆内接四边形的一个外角等于它的内对角.
几何语言
∵∠EAD是圆内接四边形ABCD的外角
∴∠EAD=∠C
求证:∠EAD=∠C
例1: 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D, 求证:DB=DC
证明:∵AD是∠EAC的平分线 ∴∠1=∠2
∵四边形ABCD内接于圆O
∴∠DCB=∠1
而∠2=∠DBC
∴∠DCB=∠DBC
∴DB=DC
(圆内接四边形的一个外角等于它的内对角).
★
★
▲
▲
新知讲解
例2 如果要把横截面直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能地大,应怎样锯?如果这根原木长15m,问锯出的木材的体积为多少立方米(树皮等损耗略去不计)?
思考:要使锯出的横截面正方形的面积尽可能大,正方形和圆
的应该满足什么关系?
正方形内接于⊙O
问题:如何画出这个正方形?
解:当原木的直径为30cm时,
∴正方形ABCD的面积为:
∴木材的体积为:4.5×10-2×15=0.675(m3).
AO=BO=15cm,
┓
A
B
C
D
圆内接四边形的外角等于内对角
圆内接四边形对角互补
一般
特殊
┓
┓
知识小结
1.四边形ABCD内接于⊙O,则∠A+∠C=______
∠B+∠ADC=_______;
若∠B=80°,
则∠ADC=______ ,
∠CDE=_________.
E
D
B
A
C
180°
180°
100°
80°
夯实基础,稳扎稳打
2.如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BAD= ,∠BCD= .
50°
130°
3.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE 的大小是( )
A.115° B.l05° C.100° D.95°
B
4、如图,点A,B,C,D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径的长是____ .
5、如图,四边形ABCD为圆的内接四边形,DA,CB的延长线交于点P,∠P=30°,∠ABC=100°,则∠C= 。
70°
.
6.如图,四边形ABCD内接于⊙O
∠A=∠C,∠B=∠D,那么四边形ABCD是怎样的特殊四边形?
∠A=∠C=∠B=∠D=900
四边形ABCD是矩形
7.若ABCD为圆内接四边形,则下列哪个选项可能成立( )
(A)∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4
(B)∠A∶∠B∶∠C∶∠D = 2∶1∶3∶4
(C)∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4
(D)∠A∶∠B∶∠C∶∠D = 4∶3∶2∶1
B
8. 在圆内接四边形ABCD中, ∠A,∠B,∠C的度数之比是2︰3︰7.求这个四边形各角的度数.
解:设∠A,∠B,∠C的度数分别对于2x,3x,7x,
∵四边形ABCD内接于圆,
∴ ∠A+ ∠C=∠B+∠D=180°,
∵2x+7x=180°,
∴ x=20°.
∴ ∠A=40°, ∠B=60°, ∠C =140°,
∠D=180°-60°=120°.
9.已知:如图,以等腰三角形ABC的底边BC为直径的☉O分别交两腰AB,AC于点D,E,连结DE.求证:DE∥BC.
证明:∵四边形BDCE是圆O的内接四边形 ∴∠ADE=∠C
∵AB=AC
∴∠B=∠C
∴∠ADE=∠B
∴DE∥BC.
连续递推,豁然开朗
10.在圆内接四边形ABCD中, 的度数之比为
1:2∶3∶4.求四边形ABCD各内角的度数.
A
B
C
D
3600×
=
︵
AC
m
=
︵
BC
m
3600×
=
︵
CD
m
3600×
=
︵
AD
m
3600×
∴ ∠A=90°, ∠B=126°,
∠C =90°,∠D=54°
连续递推,豁然开朗
.
11.已知四边形ABCD的内角∠A, ∠ B, ∠ C, ∠ D的度数之比为3:1:2:5,判断这个四边形是不是圆内接四边形,并说明理由.
3+2≠1+5
四边形是不是圆内接四边形
12.在圆内接四边形ABCD中,已知∠A=50° ∠D- ∠ B=40°.求∠ B, ∠ C, ∠ D的度数.
∠C=180°-∠A=180°-50°=1300
.
.
圆内接平行四边形一定是矩形
A
B
C
D
︵
CD
=
︵
AB
∴
∵AD=BC
︵
BC
=
︵
AD
∴
∵AB=CD
分析:
∴∠ABCD
=900
13.证明:圆内接平行四边形一定是矩形
14、如图 ,⊙O是正方形 ABCD的外接圆,点 P 在⊙O上,则∠APB等于( )
A 30° B 45° C 55° D 60°
B
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
