3.1 圆 (2) 课件(共23张PPT)
文档属性
| 名称 | 3.1 圆 (2) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 21:14:36 | ||
图片预览








文档简介
(共23张PPT)
浙教版九年级上册
3.1 圆 (2)
新知导入
问题:你有什么方法使得“破镜重圆”呢?
和圆有关的成语:
自圆其说
花好月圆
字正腔圆
外圆内方
阖家团圆
不以规矩,不成方圆
破镜重圆……
●A
经过一点可以作无数条直线;
经过两点只能作一条直线.
●A
●B
21cnjy.com
21cnjy.com
21世纪教育网
1、过一点可以作几条直线?
2、过几点可确定一条直线?
类比思想
A
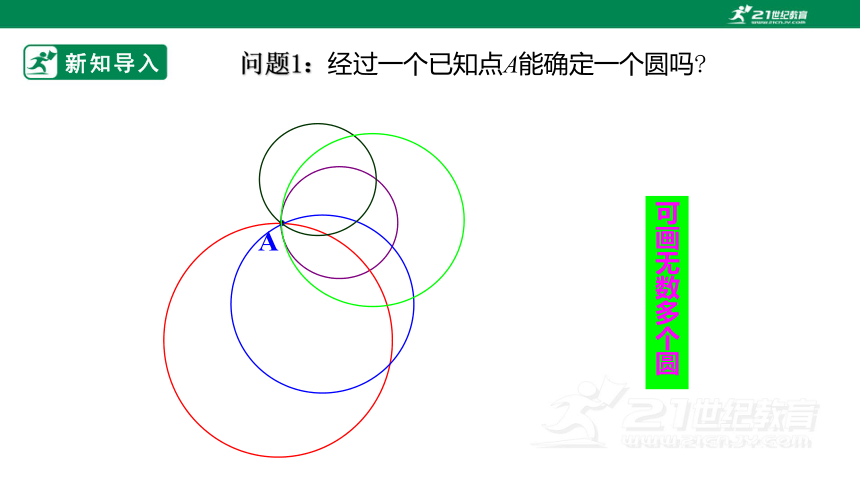
问题1:经过一个已知点A能确定一个圆吗
可画无数多个圆
新知导入
A
B
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上
问题2:过A、B两点能画几个圆呢
经过两个已知点A、B能作无数个圆
这些圆的圆心在连接两点的线段的垂直平分线上。
新知导入
假设经过A、B、C三点的⊙O存在
(1)圆心O到A、B、C三点距离 (填“相等”或”不相等”)。
(2)连结AB、AC,过O点 分别作直线MN⊥AB, EF⊥AC,则MN是AB的 ;EF是AC的 。
(3)AB、AC的中垂线的交点O到B、C的距离 。
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
问题3:经过不在同一直线的三个已知点A、B、C能否作圆
若能,能作多少个圆
新知导入
以O为圆心,OA(或OB,或OC)为半径,作⊙O即可.
请你证明你做得圆符合要求.
证明:∵点O在AB的垂直平分线上,
∴⊙O就是所求作的圆,
∴OA=OB.
同理,OB=OC.
∴OA=OB=OC.
∴点A,B,C在以O为圆心的圆上.
┓
E
D
┏
G
F
●A
●B
●C
O
新知讲解
分别作AB、BC的垂直平分线,交于一点O,
从上述作图中可以看出A、B、C三点不在一条直线上,那么在同一直线的三点能作圆吗?为什么?
A
B
C
根据作圆的方法,分别作两点连线的垂直平分线,交于一点,而三点共线的情况,任意两条垂直平分线都不可能相交,所以在同一条直线的三点不能作圆。
新知讲解
例2、已知△ABC,用直尺和圆规作出过点A,B,C的圆.
A
B
C
新知讲解
O
N
M
F
E
A
B
C
作法:
1.作线段AB的垂直平分线MN;
2.作线段AC的垂直平分线EF,交MN于点O;
3.连接OB.
4.以O为圆心,OB为半径作圆.
⊙O就是所求作的圆.
21cnjy.com
21cnjy.com
21世纪教育网
新知讲解
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
C
A
B
O
三角形的外接圆
多边形的顶点与圆的位置关系称为接.
新知讲解
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
例3:分别作出锐角三角形,直角三角形,钝角三角形的外接圆,
并说明与它们外心的位置情况
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
新知讲解
1、确定圆的条件:不在同一条直线上的三个点确定一个圆
2、三角形的外接圆:经过三角形各个顶点的圆叫做三角形的外接圆,
这个外接圆的圆心叫做三角形的外心,三角形叫做圆的内接三角形.
4、锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.
3.三角形的外心是三角形三条边的垂直平分线的交点,
它到三角形三个顶点的距离相等.
归纳总结
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
归纳总结
夯实基础,稳扎稳打
1、下列关于外心的说法正确的是( )
A.外心是三个角的平分线的交点
B.外心是三条高的交点
C.外心是三条中线的交点
D.外心是三边的垂直平分线的交点
2、等腰三角形底边上的中线所在的直线与一腰的垂直平分线的交点是( )
A.重心 B.垂心 C.外心 D.无法确定
D
C
3、如图, EF所在的直线垂直平分线段AB,利用这样的工具,最少使用 次,就可找到圆形工件的圆心.
为什么同一个圆中的两条直径的交点就是圆心?
两
直径:经过圆心的弦
圆:一中同长也。
4、若等腰直角三角形的直角边长为2cm ,则它的外接圆面积为_________.
5、边长为2的等边 三角形内接于圆O ,则圆心O到 一边的距离为________。
6、如果三角形三条边长分别为5,12,13 ,那么这个三角形外接圆半径的长为_____。
2πcm2
6.5
.
7.已知圆上两点A, B(如图),用直尺和圆规求作以AB为底边的圆内接等腰三角形,这样的三角形能作几个?
以AB为底边的等腰三角形可作两个;
8.如图,AB,CD为⊙O的两条直径,E,F分别为OA,OB的中点.求证:四边形CEDF为平行四边形.
连续递推,豁然开朗
9、如图,A,B,C表示三个工厂,要建一个供水站,使它到这三个工厂的距离相等,求作供水站的位置。
解:连接AB,BC,分别作AB,BC的线段垂直平分线,垂直平分线的交点即为供水站的位置。
如图:
10、如图所示,BD,CE是△ABC 的高,求证:E,B,C,D四点在同一个圆上.
证明:如图所示,取BC的中点F,连接DF,EF.
∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF.
∴E,B,C,D四点在以F点为圆心,BC为半径的圆上.
.
11.如图,△ABC的外接圆的圆心的坐标是 。
12、(1) 已知一个矩形ABCD,能否画出一个圆,使它的四个顶点都在同一个圆上?
试一试.
(2) 已知一个等腰梯形ABCD,能否画出一个圆,使它的四个顶点都在同一个圆上?
试一试.
(3) 已知一个平行四边形ABCD,能否画出一个圆,使它的四个顶点都在同一个圆上?
13. 如图所示,在△ABC中,AB=AC=10,BC=12,
求△ABC的外接圆半径.
思维拓展,更上一层
o
D
(8-r)2+62=r2
r=
.
浙教版九年级上册
3.1 圆 (2)
新知导入
问题:你有什么方法使得“破镜重圆”呢?
和圆有关的成语:
自圆其说
花好月圆
字正腔圆
外圆内方
阖家团圆
不以规矩,不成方圆
破镜重圆……
●A
经过一点可以作无数条直线;
经过两点只能作一条直线.
●A
●B
21cnjy.com
21cnjy.com
21世纪教育网
1、过一点可以作几条直线?
2、过几点可确定一条直线?
类比思想
A
问题1:经过一个已知点A能确定一个圆吗
可画无数多个圆
新知导入
A
B
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上
问题2:过A、B两点能画几个圆呢
经过两个已知点A、B能作无数个圆
这些圆的圆心在连接两点的线段的垂直平分线上。
新知导入
假设经过A、B、C三点的⊙O存在
(1)圆心O到A、B、C三点距离 (填“相等”或”不相等”)。
(2)连结AB、AC,过O点 分别作直线MN⊥AB, EF⊥AC,则MN是AB的 ;EF是AC的 。
(3)AB、AC的中垂线的交点O到B、C的距离 。
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
问题3:经过不在同一直线的三个已知点A、B、C能否作圆
若能,能作多少个圆
新知导入
以O为圆心,OA(或OB,或OC)为半径,作⊙O即可.
请你证明你做得圆符合要求.
证明:∵点O在AB的垂直平分线上,
∴⊙O就是所求作的圆,
∴OA=OB.
同理,OB=OC.
∴OA=OB=OC.
∴点A,B,C在以O为圆心的圆上.
┓
E
D
┏
G
F
●A
●B
●C
O
新知讲解
分别作AB、BC的垂直平分线,交于一点O,
从上述作图中可以看出A、B、C三点不在一条直线上,那么在同一直线的三点能作圆吗?为什么?
A
B
C
根据作圆的方法,分别作两点连线的垂直平分线,交于一点,而三点共线的情况,任意两条垂直平分线都不可能相交,所以在同一条直线的三点不能作圆。
新知讲解
例2、已知△ABC,用直尺和圆规作出过点A,B,C的圆.
A
B
C
新知讲解
O
N
M
F
E
A
B
C
作法:
1.作线段AB的垂直平分线MN;
2.作线段AC的垂直平分线EF,交MN于点O;
3.连接OB.
4.以O为圆心,OB为半径作圆.
⊙O就是所求作的圆.
21cnjy.com
21cnjy.com
21世纪教育网
新知讲解
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
C
A
B
O
三角形的外接圆
多边形的顶点与圆的位置关系称为接.
新知讲解
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
例3:分别作出锐角三角形,直角三角形,钝角三角形的外接圆,
并说明与它们外心的位置情况
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
新知讲解
1、确定圆的条件:不在同一条直线上的三个点确定一个圆
2、三角形的外接圆:经过三角形各个顶点的圆叫做三角形的外接圆,
这个外接圆的圆心叫做三角形的外心,三角形叫做圆的内接三角形.
4、锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.
3.三角形的外心是三角形三条边的垂直平分线的交点,
它到三角形三个顶点的距离相等.
归纳总结
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
归纳总结
夯实基础,稳扎稳打
1、下列关于外心的说法正确的是( )
A.外心是三个角的平分线的交点
B.外心是三条高的交点
C.外心是三条中线的交点
D.外心是三边的垂直平分线的交点
2、等腰三角形底边上的中线所在的直线与一腰的垂直平分线的交点是( )
A.重心 B.垂心 C.外心 D.无法确定
D
C
3、如图, EF所在的直线垂直平分线段AB,利用这样的工具,最少使用 次,就可找到圆形工件的圆心.
为什么同一个圆中的两条直径的交点就是圆心?
两
直径:经过圆心的弦
圆:一中同长也。
4、若等腰直角三角形的直角边长为2cm ,则它的外接圆面积为_________.
5、边长为2的等边 三角形内接于圆O ,则圆心O到 一边的距离为________。
6、如果三角形三条边长分别为5,12,13 ,那么这个三角形外接圆半径的长为_____。
2πcm2
6.5
.
7.已知圆上两点A, B(如图),用直尺和圆规求作以AB为底边的圆内接等腰三角形,这样的三角形能作几个?
以AB为底边的等腰三角形可作两个;
8.如图,AB,CD为⊙O的两条直径,E,F分别为OA,OB的中点.求证:四边形CEDF为平行四边形.
连续递推,豁然开朗
9、如图,A,B,C表示三个工厂,要建一个供水站,使它到这三个工厂的距离相等,求作供水站的位置。
解:连接AB,BC,分别作AB,BC的线段垂直平分线,垂直平分线的交点即为供水站的位置。
如图:
10、如图所示,BD,CE是△ABC 的高,求证:E,B,C,D四点在同一个圆上.
证明:如图所示,取BC的中点F,连接DF,EF.
∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF.
∴E,B,C,D四点在以F点为圆心,BC为半径的圆上.
.
11.如图,△ABC的外接圆的圆心的坐标是 。
12、(1) 已知一个矩形ABCD,能否画出一个圆,使它的四个顶点都在同一个圆上?
试一试.
(2) 已知一个等腰梯形ABCD,能否画出一个圆,使它的四个顶点都在同一个圆上?
试一试.
(3) 已知一个平行四边形ABCD,能否画出一个圆,使它的四个顶点都在同一个圆上?
13. 如图所示,在△ABC中,AB=AC=10,BC=12,
求△ABC的外接圆半径.
思维拓展,更上一层
o
D
(8-r)2+62=r2
r=
.
同课章节目录
