3.1 圆 (1) 课件(共25张PPT)
文档属性
| 名称 | 3.1 圆 (1) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
3.1 圆
浙教版九年级上册
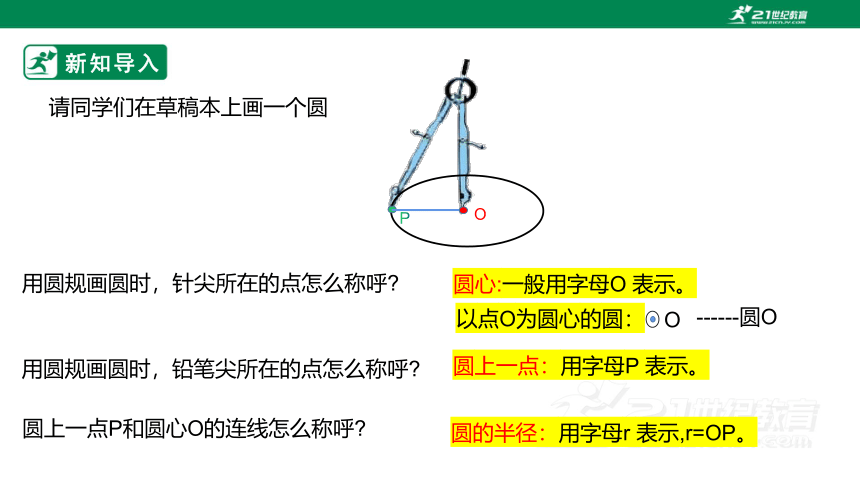
新知导入
请问在座的每一位同学,看到了什么?
圆
新知导入
用圆规画圆时,针尖所在的点怎么称呼
请同学们在草稿本上画一个圆
O
圆心:一般用字母O 表示。
P
用圆规画圆时,铅笔尖所在的点怎么称呼
圆上一点:用字母P 表示。
圆上一点P和圆心O的连线怎么称呼
圆的半径:用字母r 表示,r=OP。
以点O为圆心的圆:
O
------圆O
新知讲解
甲乙两位同学要在平坦的操场上画一个半径为3m的圆,该如何操作?
(1) 取一根3m长的绳子
(2)甲固定绳子的一端
(3)乙拿绳子的另一端,把绳子拉直,绕甲转一圈
请同学们给圆下一个定义:
O
3m
P
(1)
线段OP绕它固定的一个端点O旋转一周,
叫做圆。
定点O叫做圆心。
线段OP叫做圆的半径。
表示:
以O为圆心的圆,记做“⊙O”,
读做“圆O”。
在同一平面内,
另一端点P所经过的封闭曲线
新知讲解
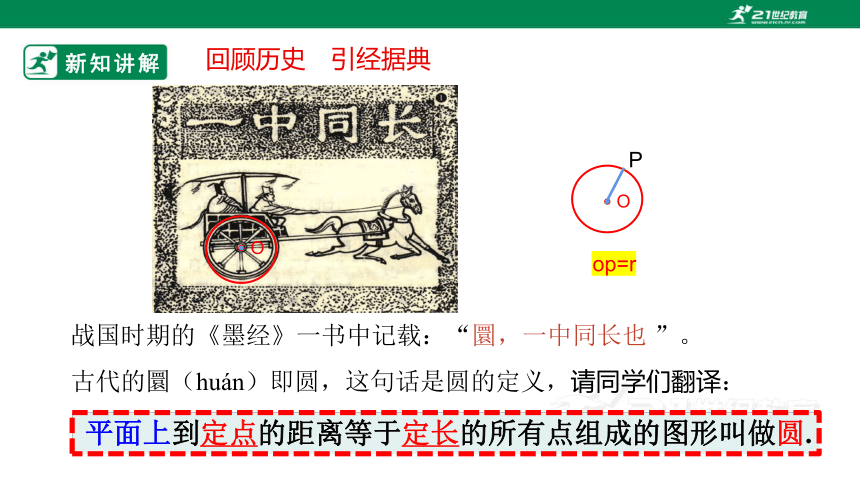
回顾历史 引经据典
战国时期的《墨经》一书中记载:“圜,一中同长也 ”。
古代的圜(huán)即圆,这句话是圆的定义,请同学们翻译:
平面上到定点的距离等于定长的所有点组成的图形叫做圆.
O
O
P
op=r
新知讲解
继续探究:在已画圆中,请同学们画出点与圆的不同位置关系:
o
o
o
p
p
p
d=r
d> r
d< r
⊙O的半径为r, 点P到圆心O的距离为d
点在圆上
点在圆内
用什么量刻画同一平面内点与圆的位置关系?
几何直观:
点在圆外
新知讲解
点
o
o
线
两点确定一条直线:射线、线段都是直线的一部分
p
Q
线段PQ有什么特征?
线段PQ两个端点在圆上
M
N
M
N
弦:
连接圆上任意两点的线段
请画一条特殊的弦
经过圆心的弦
直径:
经过圆心的弦
Q
R
P
比较直径QR与不是直径的弦QP的长短
QR >QP
几何直观+
三角形两边之和大于第三边
=OQ+OP
o
R
Q
新知讲解
两点间的部分
o
p
Q
o
Q
R
直径QR把圆分成相等两部分
半圆 ----------------
图形的折叠
图形的轴对称
你是怎么知道的?
M
┛
N
T
红色的弧,有何特征?
小于半圆,
给个称呼?
劣弧:
⌒
PQ
绿色的弧,有何特征?
大于半圆,
给个称呼?
优弧:
⌒
PMQ
M
⌒
QMR
⌒
QNR
新知讲解
确定一个圆的要素:
两张图片中的圆各有什么特征
半径相等,圆心不同
圆心相同,半径不等
圆心与半径
等圆
同心圆
新知讲解
o
p
Q
o
N
M
o
N
M
⌒
PQ
⌒
MN
等弧:
能够重合的圆弧
半径相等的两个圆能够重合,我们把它们叫做等圆
类似地,我们把能够完全重合的圆弧叫做等弧
新知讲解
例1 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑。因施工需要,必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
(1) ∠A=900,
BC=
.
(2) D 是斜边BC的中点 AD= =
.
AB=80cm, AC=100cm
综上:爆破影响面的半径应小于
.
(3)AD =
.
圈划审题:
例2:如图,在⊙O中,OA,OB是半径,C,D为OA,OB上的两点,
且AC=BD,求证:AD=BC.
导引:
要证AD=BC,只需证其所在的三角形全等,
即只需证△ADO ≌△BCO.
证明:
∵OA,OB是半径,∴OA=OB.
又∵AC=BD,∴OA-AC=OB-BD, OC=OD.
圆,一中同长也--------圆的半径相等
∴AD=BC.
在△ADO和△BCO中,
∴△ADO≌△BCO (SAS).
.
(1)确定一个圆需要两个要素,一是圆心,二是半径.圆心定其位置,半径定其大小.
知识小结:
(2)圆是一条封闭的曲线,曲线是“圆周”,而不能认为是 “圆面”.
(3)“圆上的点”指圆周上的点,“点在圆上”和“圆过点”表示的意义都是:这个点在 圆周上.
(4)到定点O的距离等于定长r的点都在同一个圆上,即到圆心的距离等于半径的点在圆上
·
O
P
夯实基础,稳扎稳打
1、判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)直径是最长的弦;
(5)等弧就是拉直以后长度相等的弧。
·
O
等弧的意义在于全等,而不是相等。
2. 已知⊙O的面积为25π
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上。
圆外
位置关系 点在圆内 点在圆上 点在圆外
数量关系 d<r d=r d>r
·
O
圆内
5
3.已知⊙O的半径是6,P为平面内的一点,请根据以下情况求OP的取值范围.
(1) 点P在圆内
(2) 点P在圆上
(3) 点P在圆外
·
O
0≤OP<6
OP=6
OP>6
(1)请找出图中所有的弦;
(2)请任选一条弦,写出这条弦所对的弧;
4.看图回答
A
B
C
O
D
弦: AC AB BC
⌒
ABC
⌒
AC
⌒
ACB
⌒
AB
⌒
BAC
⌒
BDC
5.在直角三角形ABC中,∠C=Rt∠,AC=3cm,AB=5cm。若以点C为圆心,画一个半径为3cm的圆,试判断点A,点B和⊙C的相互位置关系。
C
A
B
点A在圆上,
点B在圆外
连续递推,豁然开朗
6.作两个等圆,使其中一个圆通过另一个圆的圆心
O1
O2
点O1怎么称呼?
(1)圆O1的圆心
(2)圆O2上的一点
你看到了什么?
等边三角形
菱形
圆,一中同长也--------圆的半径相等
7.如图,在 ABC中,∠BAC=Rt∠,AO是BC边上的中线,BC为 O的直径。
(1)点A是否在圆上?请说明理由
(2)写出圆中所有的劣弧和优弧
C
B
A
O
圈划审题:
(1) AO=
点A到圆心O的距离与圆的半径相等
点A在圆上
(2)劣弧:
优弧:
⌒
AC
⌒
AB
⌒
ABC
⌒
ACB
直角三角形斜边上的中线等于斜边的一半(三连等)
8.在 ABC中,已知AB=AC=4cm,BC=6cm,P是BC的中点。以P为圆心作一个半径为3cm的圆。试判断点A,B,C与 P的位置关系,并说明理由
A
B
C
P
PB=PC=3 (cm)
点A在 P内
点B,C在 P上
圈划审题:
等腰三角形三线合一
PA=
.
9.如图, AB为 ⊙O 的直径, 点C, D在⊙O上, 已知∠BOC=70°,AD∥OC,
则∠AOD=________.
导引:
∵AD∥OC,
∴∠DAO=∠BOC=70°.
又∵OA=OD,
∴∠ADO=∠DAO=70°.
∴∠AOD=180°-∠ADO-∠DAO=40°.
40°
思维拓展,更上一层
10.如图,在A岛附近,半径约250km的范围内是一暗礁区,往北300km有一灯塔B,往西400km有一灯塔C。现有一渔船沿CB航行,问渔船会进入暗礁区吗?
有用捕捉+有关提取:
∠BAC=900, BC=
.
240<250
点D是CB上离A点最近的点,
AD的距离小于250km,渔船会进入暗礁区
AD==
.
11.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.求:
(1)∠AOB的度数;
(2)∠EOD的度数.
解:∵AB=OC,OB=OC,∴AB=OB.∴∠AOB=∠A=20°.
∵∠OBE=∠A+∠AOB,∴∠OBE=2∠A.
∵OB=OE,∴∠OBE=∠E.
∴∠E=2∠A.∴∠EOD=∠A+∠E=3∠A=60°.
3.1 圆
浙教版九年级上册
新知导入
请问在座的每一位同学,看到了什么?
圆
新知导入
用圆规画圆时,针尖所在的点怎么称呼
请同学们在草稿本上画一个圆
O
圆心:一般用字母O 表示。
P
用圆规画圆时,铅笔尖所在的点怎么称呼
圆上一点:用字母P 表示。
圆上一点P和圆心O的连线怎么称呼
圆的半径:用字母r 表示,r=OP。
以点O为圆心的圆:
O
------圆O
新知讲解
甲乙两位同学要在平坦的操场上画一个半径为3m的圆,该如何操作?
(1) 取一根3m长的绳子
(2)甲固定绳子的一端
(3)乙拿绳子的另一端,把绳子拉直,绕甲转一圈
请同学们给圆下一个定义:
O
3m
P
(1)
线段OP绕它固定的一个端点O旋转一周,
叫做圆。
定点O叫做圆心。
线段OP叫做圆的半径。
表示:
以O为圆心的圆,记做“⊙O”,
读做“圆O”。
在同一平面内,
另一端点P所经过的封闭曲线
新知讲解
回顾历史 引经据典
战国时期的《墨经》一书中记载:“圜,一中同长也 ”。
古代的圜(huán)即圆,这句话是圆的定义,请同学们翻译:
平面上到定点的距离等于定长的所有点组成的图形叫做圆.
O
O
P
op=r
新知讲解
继续探究:在已画圆中,请同学们画出点与圆的不同位置关系:
o
o
o
p
p
p
d=r
d> r
d< r
⊙O的半径为r, 点P到圆心O的距离为d
点在圆上
点在圆内
用什么量刻画同一平面内点与圆的位置关系?
几何直观:
点在圆外
新知讲解
点
o
o
线
两点确定一条直线:射线、线段都是直线的一部分
p
Q
线段PQ有什么特征?
线段PQ两个端点在圆上
M
N
M
N
弦:
连接圆上任意两点的线段
请画一条特殊的弦
经过圆心的弦
直径:
经过圆心的弦
Q
R
P
比较直径QR与不是直径的弦QP的长短
QR >QP
几何直观+
三角形两边之和大于第三边
=OQ+OP
o
R
Q
新知讲解
两点间的部分
o
p
Q
o
Q
R
直径QR把圆分成相等两部分
半圆 ----------------
图形的折叠
图形的轴对称
你是怎么知道的?
M
┛
N
T
红色的弧,有何特征?
小于半圆,
给个称呼?
劣弧:
⌒
PQ
绿色的弧,有何特征?
大于半圆,
给个称呼?
优弧:
⌒
PMQ
M
⌒
QMR
⌒
QNR
新知讲解
确定一个圆的要素:
两张图片中的圆各有什么特征
半径相等,圆心不同
圆心相同,半径不等
圆心与半径
等圆
同心圆
新知讲解
o
p
Q
o
N
M
o
N
M
⌒
PQ
⌒
MN
等弧:
能够重合的圆弧
半径相等的两个圆能够重合,我们把它们叫做等圆
类似地,我们把能够完全重合的圆弧叫做等弧
新知讲解
例1 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑。因施工需要,必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
(1) ∠A=900,
BC=
.
(2) D 是斜边BC的中点 AD= =
.
AB=80cm, AC=100cm
综上:爆破影响面的半径应小于
.
(3)AD =
.
圈划审题:
例2:如图,在⊙O中,OA,OB是半径,C,D为OA,OB上的两点,
且AC=BD,求证:AD=BC.
导引:
要证AD=BC,只需证其所在的三角形全等,
即只需证△ADO ≌△BCO.
证明:
∵OA,OB是半径,∴OA=OB.
又∵AC=BD,∴OA-AC=OB-BD, OC=OD.
圆,一中同长也--------圆的半径相等
∴AD=BC.
在△ADO和△BCO中,
∴△ADO≌△BCO (SAS).
.
(1)确定一个圆需要两个要素,一是圆心,二是半径.圆心定其位置,半径定其大小.
知识小结:
(2)圆是一条封闭的曲线,曲线是“圆周”,而不能认为是 “圆面”.
(3)“圆上的点”指圆周上的点,“点在圆上”和“圆过点”表示的意义都是:这个点在 圆周上.
(4)到定点O的距离等于定长r的点都在同一个圆上,即到圆心的距离等于半径的点在圆上
·
O
P
夯实基础,稳扎稳打
1、判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)直径是最长的弦;
(5)等弧就是拉直以后长度相等的弧。
·
O
等弧的意义在于全等,而不是相等。
2. 已知⊙O的面积为25π
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上。
圆外
位置关系 点在圆内 点在圆上 点在圆外
数量关系 d<r d=r d>r
·
O
圆内
5
3.已知⊙O的半径是6,P为平面内的一点,请根据以下情况求OP的取值范围.
(1) 点P在圆内
(2) 点P在圆上
(3) 点P在圆外
·
O
0≤OP<6
OP=6
OP>6
(1)请找出图中所有的弦;
(2)请任选一条弦,写出这条弦所对的弧;
4.看图回答
A
B
C
O
D
弦: AC AB BC
⌒
ABC
⌒
AC
⌒
ACB
⌒
AB
⌒
BAC
⌒
BDC
5.在直角三角形ABC中,∠C=Rt∠,AC=3cm,AB=5cm。若以点C为圆心,画一个半径为3cm的圆,试判断点A,点B和⊙C的相互位置关系。
C
A
B
点A在圆上,
点B在圆外
连续递推,豁然开朗
6.作两个等圆,使其中一个圆通过另一个圆的圆心
O1
O2
点O1怎么称呼?
(1)圆O1的圆心
(2)圆O2上的一点
你看到了什么?
等边三角形
菱形
圆,一中同长也--------圆的半径相等
7.如图,在 ABC中,∠BAC=Rt∠,AO是BC边上的中线,BC为 O的直径。
(1)点A是否在圆上?请说明理由
(2)写出圆中所有的劣弧和优弧
C
B
A
O
圈划审题:
(1) AO=
点A到圆心O的距离与圆的半径相等
点A在圆上
(2)劣弧:
优弧:
⌒
AC
⌒
AB
⌒
ABC
⌒
ACB
直角三角形斜边上的中线等于斜边的一半(三连等)
8.在 ABC中,已知AB=AC=4cm,BC=6cm,P是BC的中点。以P为圆心作一个半径为3cm的圆。试判断点A,B,C与 P的位置关系,并说明理由
A
B
C
P
PB=PC=3 (cm)
点A在 P内
点B,C在 P上
圈划审题:
等腰三角形三线合一
PA=
.
9.如图, AB为 ⊙O 的直径, 点C, D在⊙O上, 已知∠BOC=70°,AD∥OC,
则∠AOD=________.
导引:
∵AD∥OC,
∴∠DAO=∠BOC=70°.
又∵OA=OD,
∴∠ADO=∠DAO=70°.
∴∠AOD=180°-∠ADO-∠DAO=40°.
40°
思维拓展,更上一层
10.如图,在A岛附近,半径约250km的范围内是一暗礁区,往北300km有一灯塔B,往西400km有一灯塔C。现有一渔船沿CB航行,问渔船会进入暗礁区吗?
有用捕捉+有关提取:
∠BAC=900, BC=
.
240<250
点D是CB上离A点最近的点,
AD的距离小于250km,渔船会进入暗礁区
AD==
.
11.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.求:
(1)∠AOB的度数;
(2)∠EOD的度数.
解:∵AB=OC,OB=OC,∴AB=OB.∴∠AOB=∠A=20°.
∵∠OBE=∠A+∠AOB,∴∠OBE=2∠A.
∵OB=OE,∴∠OBE=∠E.
∴∠E=2∠A.∴∠EOD=∠A+∠E=3∠A=60°.
同课章节目录
