3.3 垂径定理 (1) 课件(共20张PPT)
文档属性
| 名称 | 3.3 垂径定理 (1) 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 21:18:25 | ||
图片预览







文档简介
(共20张PPT)
浙教版九年级上册
3.3 垂径定理 (1)
1.如图,在透明纸上任意作一个圆,☉O内作弦AB,再作一条和弦AB垂直的直径CD,AB与CD相交于点E,然后沿着直径CD所在的直线把纸折叠,你发现哪些点、线段、圆弧互相重合
·
O
A
B
D
E
C
线段: AE=BE
弧: AC=BC, AD=BD
⌒
⌒
⌒
⌒
理由如下:
把圆沿着直径CD折叠时,CD两侧的两个半圆重合,
点A与点B重合,AE与BE重合,AC和BC,AD与BD重合.
点:点A与点B
导入新知
请用文字叙述这一定理:
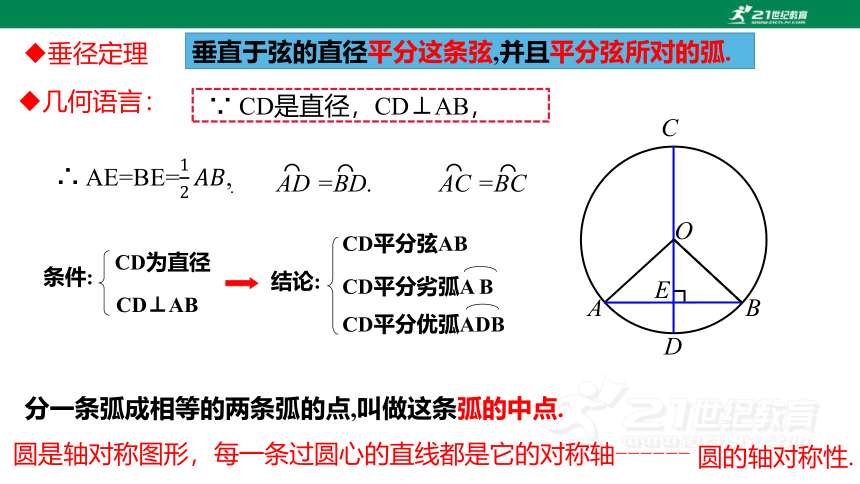
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
几何语言:
∵ CD是直径,CD⊥AB,
⌒
⌒
AD =BD.
·
O
A
B
C
D
E
分一条弧成相等的两条弧的点,叫做这条弧的中点.
⌒
⌒
AC =BC
圆是轴对称图形,每一条过圆心的直线都是它的对称轴------
∴ AE=BE=,
.
条件:
CD为直径
CD⊥AB
CD平分优弧ADB
CD平分弦AB
CD平分劣弧A B
结论:
圆的轴对称性.
例1 已知弧AB,如图,用直尺和圆规求作这条弧的中点.
A
B
C
D
E
作法:
1.连结AB.
2.作AB的垂直平分线 CD,交弧AB于点E.
如图所示,点E就是所求弧AB的中点.
例2 一条排水管的截面如图所示。已知排水管的半径OB=10,水面宽AB=16,求截面圆心O到水面的距离。
圆心到圆的一条弦的距离叫做弦心距.
例如:上图中,OC的长就是弦AB的弦心距.
O
A
B
C
垂径定理的几个基本图形
归纳总结
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂直于弦的直径:
可以是直径,
也可以是半径
甚至可以是过圆心的直线或线段
设 ⊙O 的半径是 r,圆心到弦的距离 d,弦长 a,
请写出三者数量关系:
O
┓
d2+( )2=r2
.
d
r
弦心距2+()2 =半径2 这三者“知二得一”.
.
1.如图,⊙O的直径为10,弦AB长为8,M是弦AB上的动点,则OM的长的取值范围是( )
A.3≤OM≤5 B.4≤OM≤5
C.3.
A
B
O
M
夯实基础,稳扎稳打
A
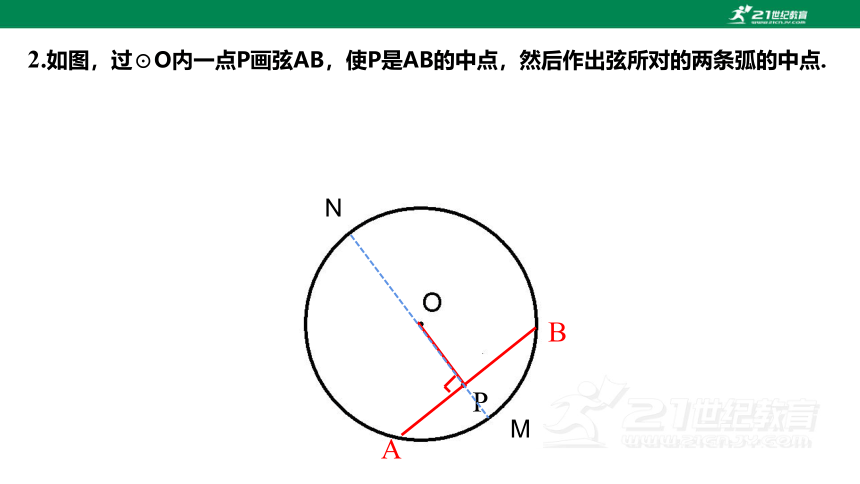
2.如图,过⊙O内一点P画弦AB,使P是AB的中点,然后作出弦所对的两条弧的中点.
P
A
B
M
N
3 (1).如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,
已知CD = 20,CM = 4,求AB的长。
┓
解:连接OA
∵ CD = 20
∴ AO = CO = 10
∴ OM = OC – CM = 10 – 4 = 6
在⊙O中,直径CD⊥弦AB
∴ AB =2AM
△OMA是Rt △
根据勾股定理,得:
∴
∴ AB = 2AM = 2 8 = 16
.
(2)绍兴是著名的桥乡,如图,圆拱桥的拱顶到水面的距离CD为8 m,
桥拱半径OC为5 m,则水面宽AB为 ( ) A.4 m B.5 m C.6 m D.8 m
D
4.如图,CD是⊙O 的直径,弦AB⊥CD于E,CE=1,AB=10,
求直径CD的长.
·
O
A
B
E
C
D
解:连接OA.
∵ CD是直径,OE⊥AB,
设OA=r,则OE=r-1,由勾股定理得
r2=52+(r-1)2 .
解得:r=13.
∴ OA=13.
∴ CD=2OA=26.
即直径CD的长为26.
弦心距2+()2 =半径2
.
∴ AE=AB=5.
.
┓
·
O
A
B
C
D
(1) 600
(2)
.
M
N
.
C
D
B
O
A
┓
┓
1.两弦在圆心的同侧
连续递推,豁然开朗
M
N
.
C
D
B
O
A
┓
┓
2.两弦在圆心的两侧
M
N
在同一个圆中,如果两弦平行,那么它们所夹的弧相等
.
C
D
B
O
A
┓
┓
3.一条弦经过圆心
8.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D, OE⊥AC于E,求证四边形ABOE是正方形.
证明:
∴四边形ADOE为矩形,
又 ∵AC=AB
∴ AE=AD
∴ 四边形ADOE为正方形.
·
O
A
B
C
D
E
9.同心圆O中,大圆的弦AB与小圆交于C,D两点,
判断线段AC与BD的大小关系,并说明理由.
解:
AC与BD相等。理由如下:
过点O作OE⊥AB于点E,
则AE=BE,CE=DE,
所以AE-CE=BE-DE,
即AC=BD.
同心圆是指两个圆的圆心相同
O
C
D
A
B
E
┓
10、已知⊙O的半径为10cm,点P是⊙O内一点,且OP=8,则过点P的所有弦中,最短的弦是( )
(A)6cm (B)8cm (C)10cm (D)12cm
D
┓
10
8
6
┓
弦心距2+()2 =半径2
.
浙教版九年级上册
3.3 垂径定理 (1)
1.如图,在透明纸上任意作一个圆,☉O内作弦AB,再作一条和弦AB垂直的直径CD,AB与CD相交于点E,然后沿着直径CD所在的直线把纸折叠,你发现哪些点、线段、圆弧互相重合
·
O
A
B
D
E
C
线段: AE=BE
弧: AC=BC, AD=BD
⌒
⌒
⌒
⌒
理由如下:
把圆沿着直径CD折叠时,CD两侧的两个半圆重合,
点A与点B重合,AE与BE重合,AC和BC,AD与BD重合.
点:点A与点B
导入新知
请用文字叙述这一定理:
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
几何语言:
∵ CD是直径,CD⊥AB,
⌒
⌒
AD =BD.
·
O
A
B
C
D
E
分一条弧成相等的两条弧的点,叫做这条弧的中点.
⌒
⌒
AC =BC
圆是轴对称图形,每一条过圆心的直线都是它的对称轴------
∴ AE=BE=,
.
条件:
CD为直径
CD⊥AB
CD平分优弧ADB
CD平分弦AB
CD平分劣弧A B
结论:
圆的轴对称性.
例1 已知弧AB,如图,用直尺和圆规求作这条弧的中点.
A
B
C
D
E
作法:
1.连结AB.
2.作AB的垂直平分线 CD,交弧AB于点E.
如图所示,点E就是所求弧AB的中点.
例2 一条排水管的截面如图所示。已知排水管的半径OB=10,水面宽AB=16,求截面圆心O到水面的距离。
圆心到圆的一条弦的距离叫做弦心距.
例如:上图中,OC的长就是弦AB的弦心距.
O
A
B
C
垂径定理的几个基本图形
归纳总结
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂直于弦的直径:
可以是直径,
也可以是半径
甚至可以是过圆心的直线或线段
设 ⊙O 的半径是 r,圆心到弦的距离 d,弦长 a,
请写出三者数量关系:
O
┓
d2+( )2=r2
.
d
r
弦心距2+()2 =半径2 这三者“知二得一”.
.
1.如图,⊙O的直径为10,弦AB长为8,M是弦AB上的动点,则OM的长的取值范围是( )
A.3≤OM≤5 B.4≤OM≤5
C.3
A
B
O
M
夯实基础,稳扎稳打
A
2.如图,过⊙O内一点P画弦AB,使P是AB的中点,然后作出弦所对的两条弧的中点.
P
A
B
M
N
3 (1).如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,
已知CD = 20,CM = 4,求AB的长。
┓
解:连接OA
∵ CD = 20
∴ AO = CO = 10
∴ OM = OC – CM = 10 – 4 = 6
在⊙O中,直径CD⊥弦AB
∴ AB =2AM
△OMA是Rt △
根据勾股定理,得:
∴
∴ AB = 2AM = 2 8 = 16
.
(2)绍兴是著名的桥乡,如图,圆拱桥的拱顶到水面的距离CD为8 m,
桥拱半径OC为5 m,则水面宽AB为 ( ) A.4 m B.5 m C.6 m D.8 m
D
4.如图,CD是⊙O 的直径,弦AB⊥CD于E,CE=1,AB=10,
求直径CD的长.
·
O
A
B
E
C
D
解:连接OA.
∵ CD是直径,OE⊥AB,
设OA=r,则OE=r-1,由勾股定理得
r2=52+(r-1)2 .
解得:r=13.
∴ OA=13.
∴ CD=2OA=26.
即直径CD的长为26.
弦心距2+()2 =半径2
.
∴ AE=AB=5.
.
┓
·
O
A
B
C
D
(1) 600
(2)
.
M
N
.
C
D
B
O
A
┓
┓
1.两弦在圆心的同侧
连续递推,豁然开朗
M
N
.
C
D
B
O
A
┓
┓
2.两弦在圆心的两侧
M
N
在同一个圆中,如果两弦平行,那么它们所夹的弧相等
.
C
D
B
O
A
┓
┓
3.一条弦经过圆心
8.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D, OE⊥AC于E,求证四边形ABOE是正方形.
证明:
∴四边形ADOE为矩形,
又 ∵AC=AB
∴ AE=AD
∴ 四边形ADOE为正方形.
·
O
A
B
C
D
E
9.同心圆O中,大圆的弦AB与小圆交于C,D两点,
判断线段AC与BD的大小关系,并说明理由.
解:
AC与BD相等。理由如下:
过点O作OE⊥AB于点E,
则AE=BE,CE=DE,
所以AE-CE=BE-DE,
即AC=BD.
同心圆是指两个圆的圆心相同
O
C
D
A
B
E
┓
10、已知⊙O的半径为10cm,点P是⊙O内一点,且OP=8,则过点P的所有弦中,最短的弦是( )
(A)6cm (B)8cm (C)10cm (D)12cm
D
┓
10
8
6
┓
弦心距2+()2 =半径2
.
同课章节目录
