3.4 圆心角(1) 课件(共28张PPT)
文档属性
| 名称 | 3.4 圆心角(1) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 00:00:00 | ||
图片预览



文档简介
(共28张PPT)
浙教版九年级上册
3.4 圆心角 (1)
把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
把圆绕圆心旋转任意一个角度,所得图形都和原图形重合.
圆是中心对称图形,圆心是它的对称中心。
O
导入新知
O
α
.
圆的旋转不变性:
圆的轴对称性:
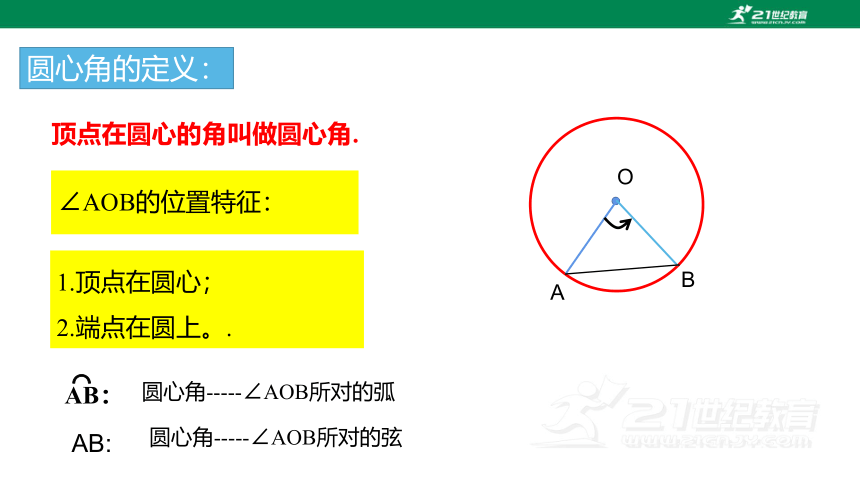
圆心角的定义:
顶点在圆心的角叫做圆心角.
∠AOB的位置特征:
O
A
B
1.顶点在圆心;
2.端点在圆上。.
AB:
⌒
圆心角-----∠AOB所对的弧
AB:
圆心角-----∠AOB所对的弦
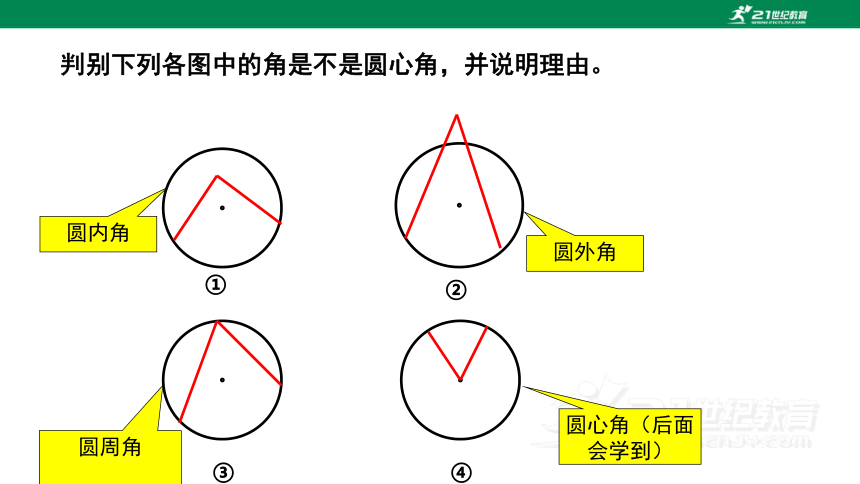
判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
圆内角
圆外角
圆周角
圆心角(后面会学到)
已知:如图,在⊙O中,∠AOB=∠COD.
证明:设∠AOC=α ∵∠AOB=∠COD
∴∠BOD=∠BOC+∠COD=∠BOC+∠AOB=α
将扇形AOB按顺时针方向旋转α角后,点A与点C重合,点B与点D重合.根据圆的旋转的性质,结论可证.
如图,在⊙O中,∠AOB=∠COD。
探索两个相等的圆心角所对的两段弧、两条弦之间都有什么关系?
圆心角、弧、弦之间的关系
在同圆中探究
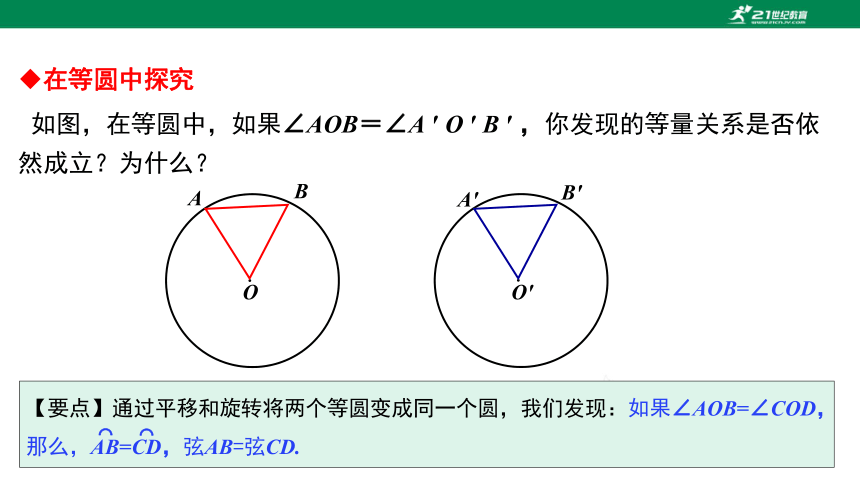
在等圆中探究
如图,在等圆中,如果∠AOB=∠A ′ O ′ B ′ ,你发现的等量关系是否依然成立?为什么?
·
O
A
B
·
O′
A′
B′
【要点】通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠COD,那么,AB=CD,弦AB=弦CD.
⌒
⌒
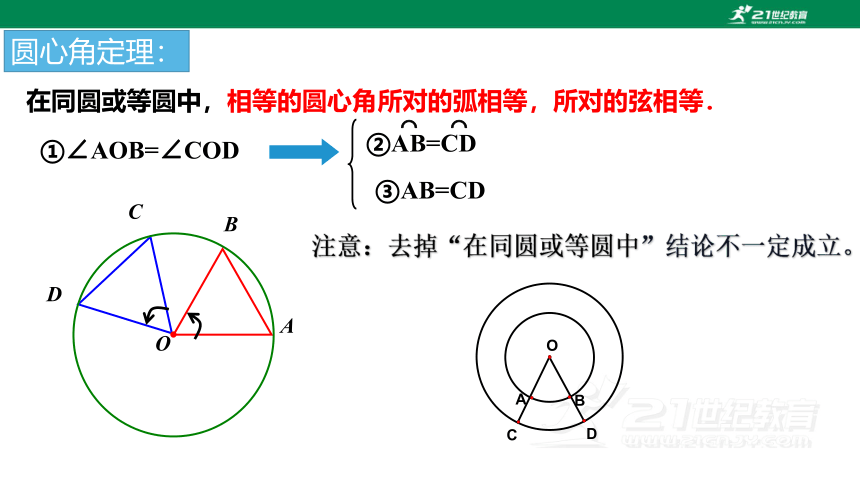
圆心角定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
A
B
O
D
C
注意:去掉“在同圆或等圆中”结论不一定成立。
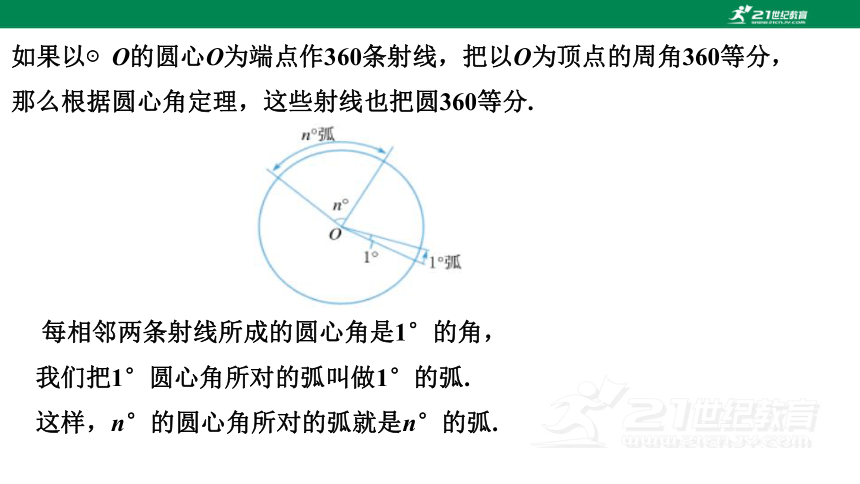
如果以⊙O的圆心O为端点作360条射线,把以O为顶点的周角360等分,那么根据圆心角定理,这些射线也把圆360等分.
每相邻两条射线所成的圆心角是1°的角,
我们把1°圆心角所对的弧叫做1°的弧.
这样,n°的圆心角所对的弧就是n°的弧.
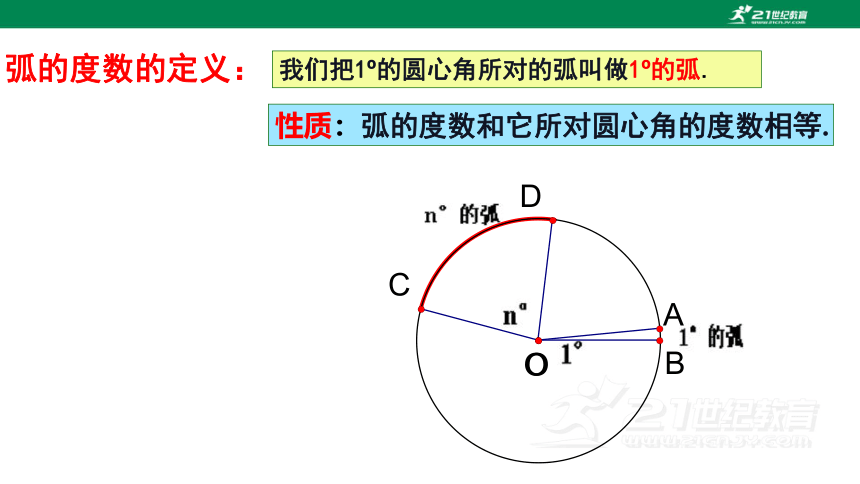
弧的度数的定义:
我们把1 的圆心角所对的弧叫做1 的弧.
性质:弧的度数和它所对圆心角的度数相等.
圆心
弧
弦
例1:用直尺和圆规把⊙O四等分.
作法:
1.作⊙O的一条直径AB.
2.过点O作CD⊥AB,交⊙O于点C和点D.
点A,B,C,D就把⊙O四等分.
C
D
A
B
例2 求证:在同圆或等圆中,相等的圆心角所对两条弦的弦心距相等.
已知:如图,在⊙O中,∠AOB=∠COD,OE是弦AB的弦心距,
OF是弦CD的弦心距. 求证:OE=OF.
证明:∵∠AOB=∠COD,∴AB=CD(圆心角定理).
∵OE⊥AB,AE=BE= AB(等腰三角形三线合一).
同理,由OF⊥DC,得DF=CF= CD.
∴AE=DF. 又∵OA=OD,
∴Rt△AOE≌Rt△DOF(HL),∴OE=OF.
.
圆心角及相关概念
1.圆心角:顶点在圆心的角,叫圆心角,如∠AOB .
2.圆心角 ∠AOB 所对的弧为 AB.
⌒
3.圆心角 ∠AOB所对的弦为AB.
任意给圆心角,对应出现四个量:
A
B
M
O
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,
所对两条弦的弦心距相等.
圆心角
弧
弦
弦心距
O
A
B
C
1.如图,在⊙O中,∠AOB=135°,求AB,ACB 的度数.
解: AB的度数=135°,
ACB的度数=360°- 135 ° =225°.
夯实基础,稳扎稳打
2.如图:已知在⊙O中,∠AOB=45°, ∠OBC=35°
则AB的度数为 .
BC的度数为 .
⌒
⌒
45
35
45°
110°
90°
4.任意画两个半径不相等的圆,然后在每一个圆上任意取一段90°的弧.这两段弧的度数相等吗?能说这两段弧相等吗?为什么?
解:任意画两个半径不相等的圆,然后在每一个圆上任意取一段90°的弧 . 这两段弧的度数相等,不能说这两段弧相等.如下图所示:
5.下列命题中正确的是( )
A.相等的圆心角所对的弦相等
B.相等的圆心角所对的弧相等
C.相等的圆心角所对的弧的度数相等
D.度数相等的两条弧相等
C
6.如图:点C为圆心,∠ACB=90°, ∠B=25°
求AD的度数
⌒
25
65
500
7. 如图,AB与CD是⊙O的直径,写出图中一对相等的弧(半圆和优弧除外).
∴ AC=BD CB=DA
⌒
⌒
⌒
⌒
B
A
C
D
O
E
1
2
解:∵OC=OD,OE⊥CD
∴∠1= ∠2
∵∠COD=1000
∴∠1=∠2=500
∴BC=500 BD=500
⌒
⌒
⌒
∴AD=ADB-BD
=1800-500
=1300
⌒
⌒
10、如图:⊙O的直径AB垂直于弦CD,AB与CD相交于点E,
∠COD=1000,求BC,AD的度数
连续递推,豁然开朗
11.如图,AC与BD为⊙O的两条互 相垂直的直径.
求证:AB=BC=CD=DA;
AB=BC=CD=DA.
⌒
⌒
⌒
⌒
O
A
B
C
D
证明: ∵AC与BD为⊙O的两条互相垂直的直径,
∴∠AOB=∠BOC=∠COD=∠DOA=90
∴ AB=BC=CD=DA
⌒
⌒
⌒
⌒
AB=BC=CD=DA(圆心角定理)
12.已知:AB为⊙O直径,AC∥OD
求证:CD=BD
要证弧(弦)相等,只需证它们所对的圆心角相等即可。
3
2
4
1
14.如图,等边三角形ABC内接于☉O,求的度数.
【答案】=120°.
.
答:CD=2AB成立,CD=2AB不成立.
取CD的中点E,连接OE.
那么∠AOB=∠COE=∠DOE,
所以AB=CE=DE, CD=2AB,
弦AB=CE=DE,在△CDE中,CE+DE>CD,即CD<2AB.
⌒ ⌒
⌒
⌒
⌒
⌒
⌒
⌒
A
B
C
D
O
E
15.如图,在⊙O中,∠COD=2∠AOB,那么CD=2AB成立吗?CD=2AB也成立吗?请说明理由;如不是,那它们之间的关系又是什么?
⌒ ⌒
思维拓展,更上一层
浙教版九年级上册
3.4 圆心角 (1)
把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
把圆绕圆心旋转任意一个角度,所得图形都和原图形重合.
圆是中心对称图形,圆心是它的对称中心。
O
导入新知
O
α
.
圆的旋转不变性:
圆的轴对称性:
圆心角的定义:
顶点在圆心的角叫做圆心角.
∠AOB的位置特征:
O
A
B
1.顶点在圆心;
2.端点在圆上。.
AB:
⌒
圆心角-----∠AOB所对的弧
AB:
圆心角-----∠AOB所对的弦
判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
圆内角
圆外角
圆周角
圆心角(后面会学到)
已知:如图,在⊙O中,∠AOB=∠COD.
证明:设∠AOC=α ∵∠AOB=∠COD
∴∠BOD=∠BOC+∠COD=∠BOC+∠AOB=α
将扇形AOB按顺时针方向旋转α角后,点A与点C重合,点B与点D重合.根据圆的旋转的性质,结论可证.
如图,在⊙O中,∠AOB=∠COD。
探索两个相等的圆心角所对的两段弧、两条弦之间都有什么关系?
圆心角、弧、弦之间的关系
在同圆中探究
在等圆中探究
如图,在等圆中,如果∠AOB=∠A ′ O ′ B ′ ,你发现的等量关系是否依然成立?为什么?
·
O
A
B
·
O′
A′
B′
【要点】通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠COD,那么,AB=CD,弦AB=弦CD.
⌒
⌒
圆心角定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
A
B
O
D
C
注意:去掉“在同圆或等圆中”结论不一定成立。
如果以⊙O的圆心O为端点作360条射线,把以O为顶点的周角360等分,那么根据圆心角定理,这些射线也把圆360等分.
每相邻两条射线所成的圆心角是1°的角,
我们把1°圆心角所对的弧叫做1°的弧.
这样,n°的圆心角所对的弧就是n°的弧.
弧的度数的定义:
我们把1 的圆心角所对的弧叫做1 的弧.
性质:弧的度数和它所对圆心角的度数相等.
圆心
弧
弦
例1:用直尺和圆规把⊙O四等分.
作法:
1.作⊙O的一条直径AB.
2.过点O作CD⊥AB,交⊙O于点C和点D.
点A,B,C,D就把⊙O四等分.
C
D
A
B
例2 求证:在同圆或等圆中,相等的圆心角所对两条弦的弦心距相等.
已知:如图,在⊙O中,∠AOB=∠COD,OE是弦AB的弦心距,
OF是弦CD的弦心距. 求证:OE=OF.
证明:∵∠AOB=∠COD,∴AB=CD(圆心角定理).
∵OE⊥AB,AE=BE= AB(等腰三角形三线合一).
同理,由OF⊥DC,得DF=CF= CD.
∴AE=DF. 又∵OA=OD,
∴Rt△AOE≌Rt△DOF(HL),∴OE=OF.
.
圆心角及相关概念
1.圆心角:顶点在圆心的角,叫圆心角,如∠AOB .
2.圆心角 ∠AOB 所对的弧为 AB.
⌒
3.圆心角 ∠AOB所对的弦为AB.
任意给圆心角,对应出现四个量:
A
B
M
O
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,
所对两条弦的弦心距相等.
圆心角
弧
弦
弦心距
O
A
B
C
1.如图,在⊙O中,∠AOB=135°,求AB,ACB 的度数.
解: AB的度数=135°,
ACB的度数=360°- 135 ° =225°.
夯实基础,稳扎稳打
2.如图:已知在⊙O中,∠AOB=45°, ∠OBC=35°
则AB的度数为 .
BC的度数为 .
⌒
⌒
45
35
45°
110°
90°
4.任意画两个半径不相等的圆,然后在每一个圆上任意取一段90°的弧.这两段弧的度数相等吗?能说这两段弧相等吗?为什么?
解:任意画两个半径不相等的圆,然后在每一个圆上任意取一段90°的弧 . 这两段弧的度数相等,不能说这两段弧相等.如下图所示:
5.下列命题中正确的是( )
A.相等的圆心角所对的弦相等
B.相等的圆心角所对的弧相等
C.相等的圆心角所对的弧的度数相等
D.度数相等的两条弧相等
C
6.如图:点C为圆心,∠ACB=90°, ∠B=25°
求AD的度数
⌒
25
65
500
7. 如图,AB与CD是⊙O的直径,写出图中一对相等的弧(半圆和优弧除外).
∴ AC=BD CB=DA
⌒
⌒
⌒
⌒
B
A
C
D
O
E
1
2
解:∵OC=OD,OE⊥CD
∴∠1= ∠2
∵∠COD=1000
∴∠1=∠2=500
∴BC=500 BD=500
⌒
⌒
⌒
∴AD=ADB-BD
=1800-500
=1300
⌒
⌒
10、如图:⊙O的直径AB垂直于弦CD,AB与CD相交于点E,
∠COD=1000,求BC,AD的度数
连续递推,豁然开朗
11.如图,AC与BD为⊙O的两条互 相垂直的直径.
求证:AB=BC=CD=DA;
AB=BC=CD=DA.
⌒
⌒
⌒
⌒
O
A
B
C
D
证明: ∵AC与BD为⊙O的两条互相垂直的直径,
∴∠AOB=∠BOC=∠COD=∠DOA=90
∴ AB=BC=CD=DA
⌒
⌒
⌒
⌒
AB=BC=CD=DA(圆心角定理)
12.已知:AB为⊙O直径,AC∥OD
求证:CD=BD
要证弧(弦)相等,只需证它们所对的圆心角相等即可。
3
2
4
1
14.如图,等边三角形ABC内接于☉O,求的度数.
【答案】=120°.
.
答:CD=2AB成立,CD=2AB不成立.
取CD的中点E,连接OE.
那么∠AOB=∠COE=∠DOE,
所以AB=CE=DE, CD=2AB,
弦AB=CE=DE,在△CDE中,CE+DE>CD,即CD<2AB.
⌒ ⌒
⌒
⌒
⌒
⌒
⌒
⌒
A
B
C
D
O
E
15.如图,在⊙O中,∠COD=2∠AOB,那么CD=2AB成立吗?CD=2AB也成立吗?请说明理由;如不是,那它们之间的关系又是什么?
⌒ ⌒
思维拓展,更上一层
同课章节目录
