3.4 圆心角 (2) 课件(共24张PPT)
文档属性
| 名称 | 3.4 圆心角 (2) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 21:19:09 | ||
图片预览



文档简介
(共24张PPT)
浙教版九年级上册
3.4 圆心角 (2)
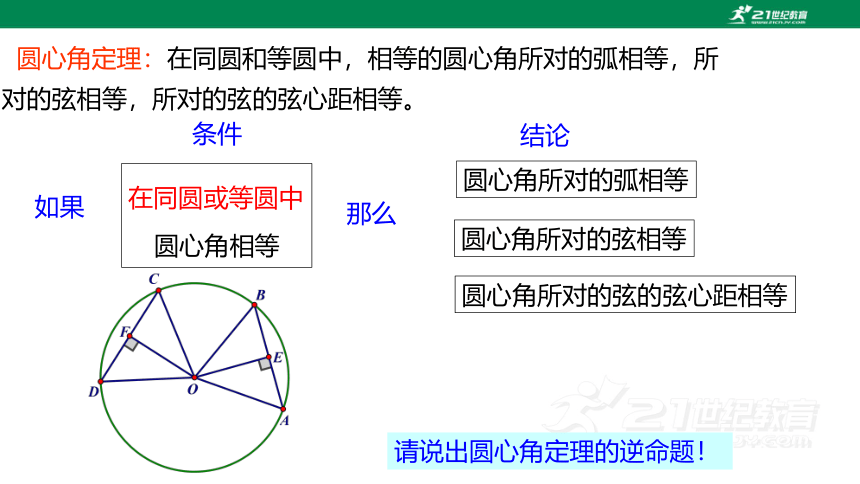
圆心角定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。
条件
如果
在同圆或等圆中
圆心角相等
那么
结论
圆心角所对的弧相等
圆心角所对的弦相等
圆心角所对的弦的弦心距相等
请说出圆心角定理的逆命题!
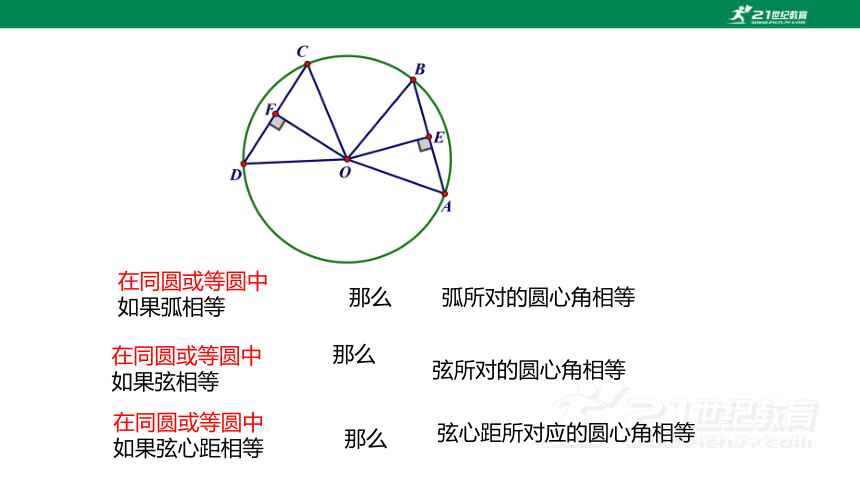
在同圆或等圆中
如果弧相等
那么
弧所对的圆心角相等
在同圆或等圆中
如果弦相等
那么
弦所对的圆心角相等
在同圆或等圆中
如果弦心距相等
那么
弦心距所对应的圆心角相等
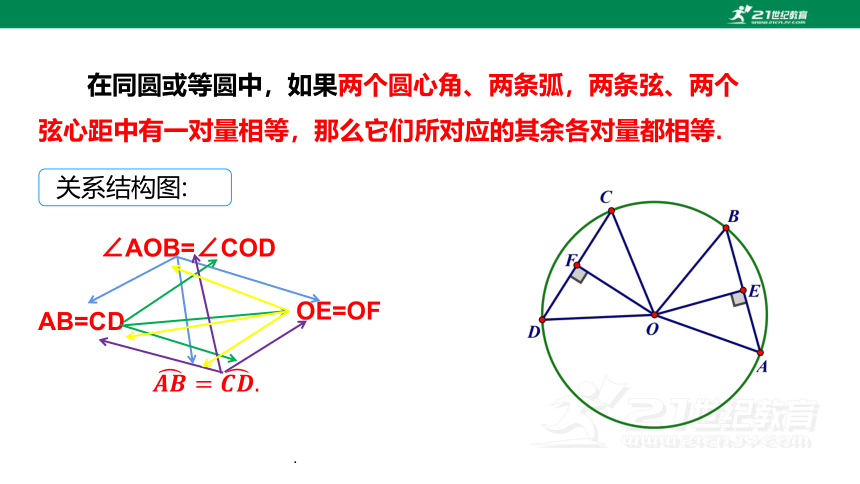
在同圆或等圆中,如果两个圆心角、两条弧,两条弦、两个弦心距中有一对量相等,那么它们所对应的其余各对量都相等.
关系结构图:
∠AOB=∠COD
AB=CD
OE=OF
.
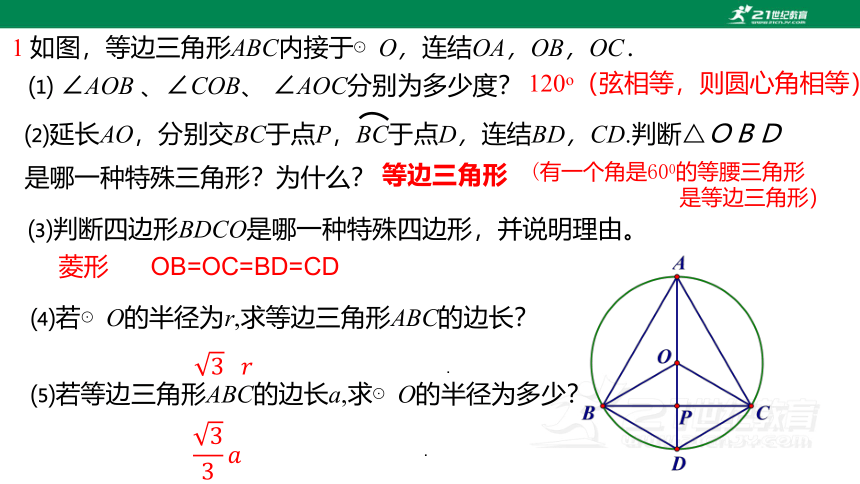
1 如图,等边三角形ABC内接于⊙O,连结OA,OB,OC.
⑴ ∠AOB 、∠COB、 ∠AOC分别为多少度?
120o(弦相等,则圆心角相等)
⑵延长AO,分别交BC于点P,BC于点D,连结BD,CD.判断△OBD是哪一种特殊三角形?为什么?
等边三角形
⑶判断四边形BDCO是哪一种特殊四边形,并说明理由。
菱形 OB=OC=BD=CD
⑷若⊙O的半径为r,求等边三角形ABC的边长?
.
⑸若等边三角形ABC的边长a,求⊙O的半径为多少?
.
(有一个角是600的等腰三角形
是等边三角形)
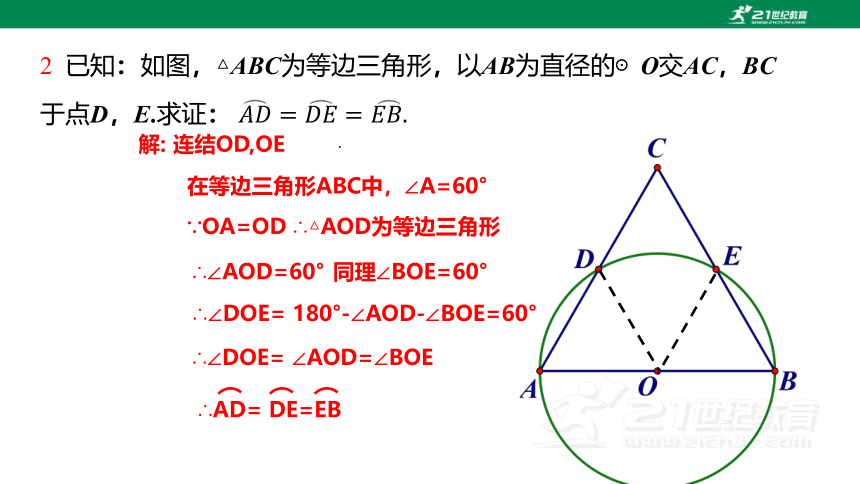
2 已知:如图,△ABC为等边三角形,以AB为直径的⊙O交AC,BC于点D,E.求证:
.
解: 连结OD,OE
在等边三角形ABC中,∠A=60°
∵OA=OD
∴△AOD为等边三角形
∴∠AOD=60°
同理∠BOE=60°
∴∠DOE= 180°-∠AOD-∠BOE=60°
∴∠DOE= ∠AOD=∠BOE
∴AD= DE=EB
圆的对称性
圆的轴对称性
(圆是轴对称图形)
垂径定理及其逆定理
圆的中心对称性
(旋转不变性)
圆心角定理及其逆定理
【点悟】 在同圆或等圆中,要证明圆心角、弧、弦、弦心距这四组量中的某一组量相等,通常是转化成证明另外三组量中的某一组量相等.
(
AB=CD
(
OM=ON
∠AOB=∠COD
∠AOB=∠COD
OM=ON
AB=CD
OM=ON
AB=CD
(
AB=CD
(
AB=CD
(
AB=CD
(
∠AOB=∠COD
(
AB=CD
(
夯实基础,稳扎稳打
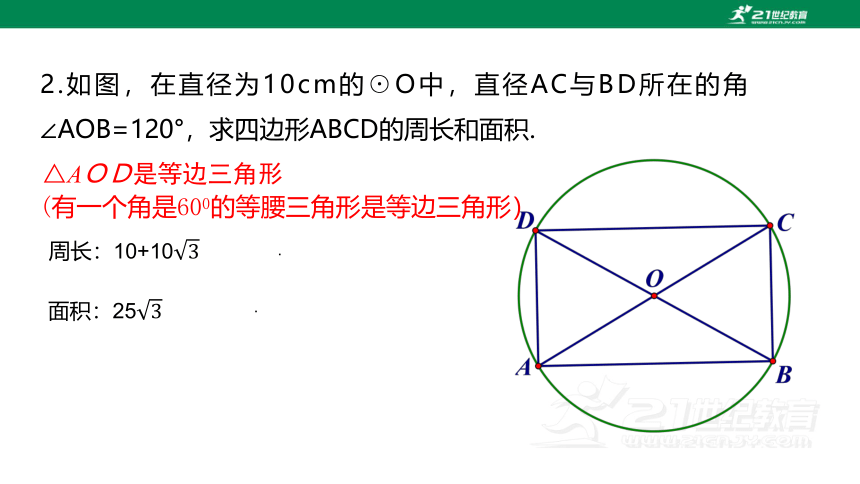
2.如图,在直径为10cm的☉O中,直径AC与BD所在的角∠AOB=120°,求四边形ABCD的周长和面积.
周长:10+10
.
面积:25
.
(有一个角是600的等腰三角形是等边三角形)
△AOD是等边三角形
证明:∵AB=CD
=
︵
AB
︵
CD
∴
在同圆中,相等的弦所对的弧相等
∴
︵
AB
︵
BD
-
=
︵
CD
︵
BD
-
︵
AD
=
即:
︵
BC
∴AD=BC
在同圆中,相等的弧所对的弦相等
变式训练:若AD=BC,那么比较AB与CD的大小.
4.如图,在⊙O中, ,∠ACB=60°.
求证:∠AOB=∠BOC=∠AOC.
证明:∵ ,
∴AB=AC
∴△ABC是等腰三角形.
∵∠ACB=60°,
∴△ABC是等边三角形(有一个角是600的等腰三角形是等边三角形),
∴AB=BC=CA.
∴∠AOB=∠BOC=∠AOC.
.
5.已知:如图,AB,DE是☉O的直径,C是☉O上一点,且求证: BE
∵ AD= CE
证明:连接OC
1
2
3
∴∠1=∠2
∵∠1=∠3
∴∠2=∠3
∴BE=CE
6.下列命题是真命题的是( )
(A)相等的圆心角所对的弧相等
(B)长度相等的两条弧是等弧
(C)等弦所对的圆心角相等
(D)等弧所对的弦相等
D
7、如图4,AB是⊙O的直径,BC=CD=DE,∠COD=35°,求∠AOE的度数。
解: ∵ BC=CD=DE
∴∠COB=∠COD=∠DOE=35°
∴∠AOE=1800-∠COB-∠COD-∠DOE
=750
O
A
B
E
D
C
9. 如图,AB,AC,BC都是⊙O的弦,且∠CAB=∠CBA,求证:∠COB=∠COA.
∵∠CAB=∠CBA
∴AC=BC
∴∠COB=∠COA.
证明:
10.已知:如图,AB,AC是☉O的两条弦,OA平分∠BAC.
求证:
┛
E
┛
D
证明: 作 , 垂足分别为D 、 E。
∵∠DAO= ∠EAO
∴ OD=OE
(角平分線上的點到線段兩端的距離相等)
∴ AB=AC
.
连续递推,豁然开朗
11.如图,已知点O是∠EPF 的平分线上一点,P点在圆外,以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D, 求证:AB=CD
P
A
B
E
C
D
F
O
分析: 联想到“角平分线的性质”,作弦心距OM、ON,
要证AB=CD ,只需证OM=ON.
证明: 作 , 垂足分别为M 、 N 。
OM=ON
AB=CD
┛
M
┛
N
如图,P点在圆内,AB=CD吗?
.
P
B
E
D
F
O
A
C
.
P
B
E
M
N
D
F
O
M
N
┛
┛
┛
┛
12、如图, AB、CD是⊙O的两条直径。
O
C
B
A
D
(1)顺次连结点A、C、B、D,所得的四边形是什么特殊四边形?为什么?
(2)四边形ACBD有可能为正方形吗?若有可能,当AB、CD有何位置关系时,四边形ACBD为正方形?为什么?
解:如图,所得的四边形是矩形,理由如下:
∵AC,BD是⊙O的直径
∴AO=OC=OB=OD
∴四边形ABCD是平行四边形
又∵AC=BD
∴四边形ABCD是矩形
当AC⊥BD时,四边形ABCD是正方形
13.已知:如图,AB,CD是⊙O的两条弦,AB=CD.
求证:∠OBA=∠ODC.
证明:过点O分别作OE⊥AB于点E,OF⊥CD于点F.
∵AB=CD,∴OE=OF.又∵BO=DO,
∴Rt△BOE≌Rt△DOF(HL),
∴∠OBA=∠ODC.
┛
E
┛
F
D
┛
思维拓展,更上一层
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
3.4 圆心角 (2)
圆心角定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。
条件
如果
在同圆或等圆中
圆心角相等
那么
结论
圆心角所对的弧相等
圆心角所对的弦相等
圆心角所对的弦的弦心距相等
请说出圆心角定理的逆命题!
在同圆或等圆中
如果弧相等
那么
弧所对的圆心角相等
在同圆或等圆中
如果弦相等
那么
弦所对的圆心角相等
在同圆或等圆中
如果弦心距相等
那么
弦心距所对应的圆心角相等
在同圆或等圆中,如果两个圆心角、两条弧,两条弦、两个弦心距中有一对量相等,那么它们所对应的其余各对量都相等.
关系结构图:
∠AOB=∠COD
AB=CD
OE=OF
.
1 如图,等边三角形ABC内接于⊙O,连结OA,OB,OC.
⑴ ∠AOB 、∠COB、 ∠AOC分别为多少度?
120o(弦相等,则圆心角相等)
⑵延长AO,分别交BC于点P,BC于点D,连结BD,CD.判断△OBD是哪一种特殊三角形?为什么?
等边三角形
⑶判断四边形BDCO是哪一种特殊四边形,并说明理由。
菱形 OB=OC=BD=CD
⑷若⊙O的半径为r,求等边三角形ABC的边长?
.
⑸若等边三角形ABC的边长a,求⊙O的半径为多少?
.
(有一个角是600的等腰三角形
是等边三角形)
2 已知:如图,△ABC为等边三角形,以AB为直径的⊙O交AC,BC于点D,E.求证:
.
解: 连结OD,OE
在等边三角形ABC中,∠A=60°
∵OA=OD
∴△AOD为等边三角形
∴∠AOD=60°
同理∠BOE=60°
∴∠DOE= 180°-∠AOD-∠BOE=60°
∴∠DOE= ∠AOD=∠BOE
∴AD= DE=EB
圆的对称性
圆的轴对称性
(圆是轴对称图形)
垂径定理及其逆定理
圆的中心对称性
(旋转不变性)
圆心角定理及其逆定理
【点悟】 在同圆或等圆中,要证明圆心角、弧、弦、弦心距这四组量中的某一组量相等,通常是转化成证明另外三组量中的某一组量相等.
(
AB=CD
(
OM=ON
∠AOB=∠COD
∠AOB=∠COD
OM=ON
AB=CD
OM=ON
AB=CD
(
AB=CD
(
AB=CD
(
AB=CD
(
∠AOB=∠COD
(
AB=CD
(
夯实基础,稳扎稳打
2.如图,在直径为10cm的☉O中,直径AC与BD所在的角∠AOB=120°,求四边形ABCD的周长和面积.
周长:10+10
.
面积:25
.
(有一个角是600的等腰三角形是等边三角形)
△AOD是等边三角形
证明:∵AB=CD
=
︵
AB
︵
CD
∴
在同圆中,相等的弦所对的弧相等
∴
︵
AB
︵
BD
-
=
︵
CD
︵
BD
-
︵
AD
=
即:
︵
BC
∴AD=BC
在同圆中,相等的弧所对的弦相等
变式训练:若AD=BC,那么比较AB与CD的大小.
4.如图,在⊙O中, ,∠ACB=60°.
求证:∠AOB=∠BOC=∠AOC.
证明:∵ ,
∴AB=AC
∴△ABC是等腰三角形.
∵∠ACB=60°,
∴△ABC是等边三角形(有一个角是600的等腰三角形是等边三角形),
∴AB=BC=CA.
∴∠AOB=∠BOC=∠AOC.
.
5.已知:如图,AB,DE是☉O的直径,C是☉O上一点,且求证: BE
∵ AD= CE
证明:连接OC
1
2
3
∴∠1=∠2
∵∠1=∠3
∴∠2=∠3
∴BE=CE
6.下列命题是真命题的是( )
(A)相等的圆心角所对的弧相等
(B)长度相等的两条弧是等弧
(C)等弦所对的圆心角相等
(D)等弧所对的弦相等
D
7、如图4,AB是⊙O的直径,BC=CD=DE,∠COD=35°,求∠AOE的度数。
解: ∵ BC=CD=DE
∴∠COB=∠COD=∠DOE=35°
∴∠AOE=1800-∠COB-∠COD-∠DOE
=750
O
A
B
E
D
C
9. 如图,AB,AC,BC都是⊙O的弦,且∠CAB=∠CBA,求证:∠COB=∠COA.
∵∠CAB=∠CBA
∴AC=BC
∴∠COB=∠COA.
证明:
10.已知:如图,AB,AC是☉O的两条弦,OA平分∠BAC.
求证:
┛
E
┛
D
证明: 作 , 垂足分别为D 、 E。
∵∠DAO= ∠EAO
∴ OD=OE
(角平分線上的點到線段兩端的距離相等)
∴ AB=AC
.
连续递推,豁然开朗
11.如图,已知点O是∠EPF 的平分线上一点,P点在圆外,以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D, 求证:AB=CD
P
A
B
E
C
D
F
O
分析: 联想到“角平分线的性质”,作弦心距OM、ON,
要证AB=CD ,只需证OM=ON.
证明: 作 , 垂足分别为M 、 N 。
OM=ON
AB=CD
┛
M
┛
N
如图,P点在圆内,AB=CD吗?
.
P
B
E
D
F
O
A
C
.
P
B
E
M
N
D
F
O
M
N
┛
┛
┛
┛
12、如图, AB、CD是⊙O的两条直径。
O
C
B
A
D
(1)顺次连结点A、C、B、D,所得的四边形是什么特殊四边形?为什么?
(2)四边形ACBD有可能为正方形吗?若有可能,当AB、CD有何位置关系时,四边形ACBD为正方形?为什么?
解:如图,所得的四边形是矩形,理由如下:
∵AC,BD是⊙O的直径
∴AO=OC=OB=OD
∴四边形ABCD是平行四边形
又∵AC=BD
∴四边形ABCD是矩形
当AC⊥BD时,四边形ABCD是正方形
13.已知:如图,AB,CD是⊙O的两条弦,AB=CD.
求证:∠OBA=∠ODC.
证明:过点O分别作OE⊥AB于点E,OF⊥CD于点F.
∵AB=CD,∴OE=OF.又∵BO=DO,
∴Rt△BOE≌Rt△DOF(HL),
∴∠OBA=∠ODC.
┛
E
┛
F
D
┛
思维拓展,更上一层
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
