3.5 圆周角 (1) 课件(共26张PPT)
文档属性
| 名称 | 3.5 圆周角 (1) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 21:27:47 | ||
图片预览







文档简介
(共26张PPT)
浙教版九年级上册
3.5 圆周角 (1)
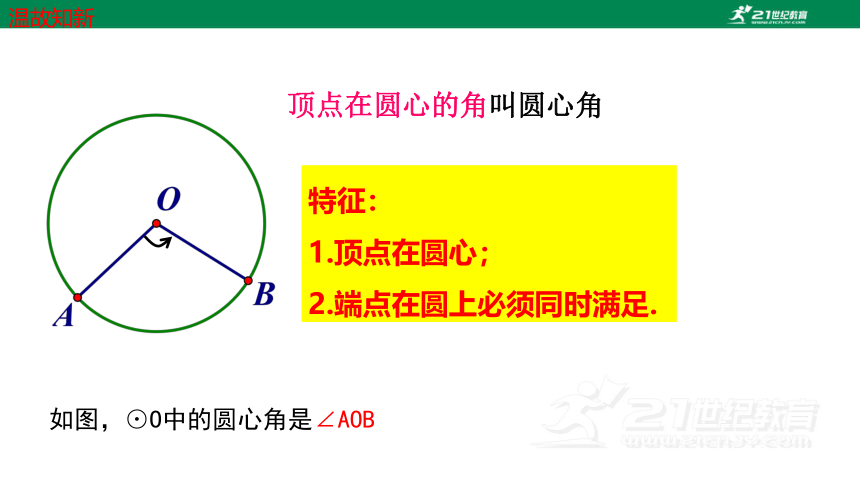
顶点在圆心的角叫圆心角
特征:
1.顶点在圆心;
2.端点在圆上必须同时满足.
如图,⊙O中的圆心角是∠AOB
温故知新
如图,∠BAC是圆周角。
圆周角:顶点在圆上,并且两边都和圆相交的角.
特征:① 角的顶点在圆周上
② 角的两边都与圆相交
再画几个BC所对的圆周角:
∠BAC: BC所对的圆周角;
D
∠BDC
顶点在圆上,且两边都和圆相交的角叫做圆周角。
下列各图中的角是圆周角的是 (填序号)。
⑤
80°
②延长AO交⊙O于点C,连结CB,
求∠C的度数。
40°
如图,在⊙O中,∠AOB=80°
①求 AB 的度数;
等腰三角形顶角的外角度数=2×底角的度数
O
A
B
C
.
圆心角:顶点在圆心的角,两边都和圆相交的角
圆周角:顶点在圆上,两边都和圆相交的角
同弧所对的圆心角与圆周角有何关系?
大胆猜想:
∠BOC=2∠BAC
同弧所对的圆周角度数=×同弧所对的圆心角度数.
.
.
∠BOC=∠BAC
.
证明:(1)当圆心O在圆周角∠BAC的一边AB上时
特殊:圆心O落在圆周角的边上!!
已知: 如图,∠BOC和∠BAC分别是 BC 所对的圆心角和圆周角
求证: ∠BAC= ∠BOC
圆周角的度数等于它所对弧上的圆心角度数的一半
∵OA=OB
∴∠A=∠ABO
∵∠BOC是△OAB的外角
∴∠BOC=∠A+∠ABO=2∠BAC
∴ ∠BAC= ∠BOC
.
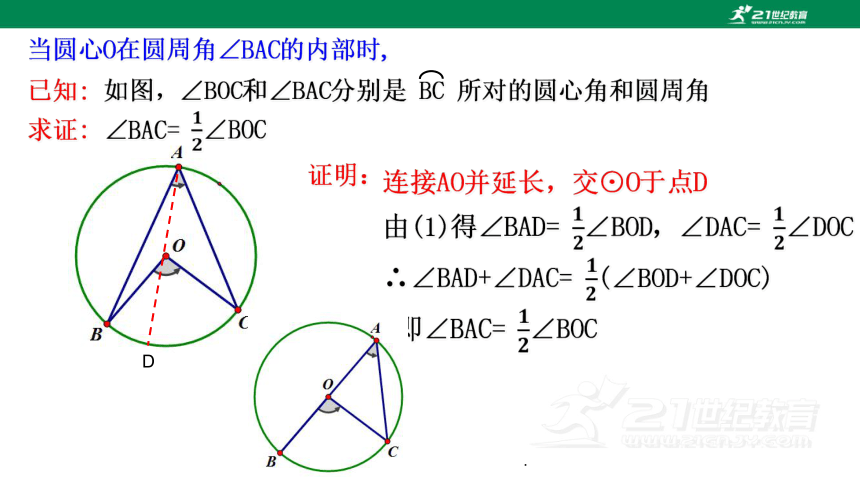
当圆心O在圆周角∠BAC的内部时,
已知: 如图,∠BOC和∠BAC分别是 BC 所对的圆心角和圆周角
求证: ∠BAC= ∠BOC
证明:
连接AO并延长,交⊙O于点D
由(1)得∠BAD= ∠BOD,∠DAC= ∠DOC
∴∠BAD+∠DAC= (∠BOD+∠DOC)
即∠BAC= ∠BOC
.
D
证明:
当圆心O在圆周角∠BAC的外部时
D
已知: 如图,∠BOC和∠BAC分别是 BC 所对的圆心角和圆周角
求证: ∠BAC= ∠BOC
连接AO并延长,交⊙O于点D
∠BAD= ∠BOD,∠DAC= ∠DOC
∴∠DAC-∠BAD= (∠DOC-∠BOD)
即∠BAC= ∠BOC
.
当点A在 上移动过程中是否满足这个关系式呢?
在移动过程中,∠BAC与圆心O有几种位置关系
程在移动过程中,∠BAC与圆心O有几种位置关系
中,∠BAC与圆心O有几种位置关系
①圆周角内
②圆周角外
③圆周角的一条边上
圆周角的度数等于它所对弧上的圆心角度数的一半
同弧所对圆周角相等
圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半
一条弧所对的圆周角等于它所对的圆心角的一半。
∵∠BAC和∠BOC都对BC
∴∠BAC= ∠BOC
⌒
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
直径对直角
直角对直径
如图,AB是直径,则∠ACB=__.
如图,∠ACB=90°,则AB为⊙O的__.
半圆(或直径)所对的圆周角是直角.
90°的圆周角所对的弦是直径.
A
O
C
B
900
直径
分类讨论的依据大多是在证明过程中产生重要影响的图形之间的相对位置。如圆周角定理的证明的分类依据是圆心和圆周角之间的相对位置。根据圆心在圆周角的角边、角内和角外,把证明分三种情况进行讨论。
角边上
角内
角外
例1 如图,等腰三角形ABC的顶角∠BAC为50°,以腰AB为直径作半圆,
交BC于点D,交AC于点E.
解: 连结BE,AD
∵ AB是圆的直径
∴∠AEB=∠ADB=90°(直径所对的圆周角是直角)
∵∠BAC=50°
∴∠ABE=90°-∠BAC=90°-50°=40°
又∵△ABC是等腰三角形,
∴∠ABC=∠C=
∠BAD=∠CAD=BAC=50°=25°
由圆周角定理,得BD2∠BAD=2×25°=50°
DE2∠CAD=2×25°=50°,AE=2∠ABE=2×40°=80°
新知讲解
1、圆周角的定义:
顶点在圆上,两边都与圆相交的角.
2、圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
3、圆周角定理的推论:
半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
归纳小结
1.图中有几个圆周角?( )
A.2个 B.3个 C.4个 D.5个
D
夯实基础,稳扎稳打
2.如图,在下列各图中,
∠α1=_________, ∠α2=_______, ∠α3=_________, ∠α4=________.
.O
(
(
α2
1200
.
(
(
300
α3
O
.
(
(
α1
750
O
.
(
(
1100
α4
37.5°
60°
120°
125°
3. 如图,若∠A=40°,则∠OBC= .
500
4.如图,在☉O中,∠AOC=140°,∠ACB=50°,求∠BAC的度数.
∵∠ACB=50°
∴∠AOB=100°
∴∠COB=∠AOC -∠AOB
=140°-100°
=40°
∴∠BAC=200
解:
n0
∠AOB=n0
.
6.如图,△ABC是☉O的内接三角形,AD是☉O的直径,∠ABC=50°,求∠CAD的度数.
∵∠ABC=50°
∵AD是☉O的直径
∠CAD=40°
.
7.已知:如图,OA是☉O的半径,以OA为直径的☉C与☉O的弦AB相交于点D,求证:AD=DB.
连续递推,豁然开朗
┛
证明:连接OD
∵AO是☉C的直径
AD=DB (垂径定理)
.
∠ODA=90°
.
OD⊥AB
.
8.在⊙O中,圆心角∠AOB=560,则弦AB所对的圆周角等于( )
A、280
B、1120
C、280或1520
D、1240或560
A
B
(
.O
C
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
3.5 圆周角 (1)
顶点在圆心的角叫圆心角
特征:
1.顶点在圆心;
2.端点在圆上必须同时满足.
如图,⊙O中的圆心角是∠AOB
温故知新
如图,∠BAC是圆周角。
圆周角:顶点在圆上,并且两边都和圆相交的角.
特征:① 角的顶点在圆周上
② 角的两边都与圆相交
再画几个BC所对的圆周角:
∠BAC: BC所对的圆周角;
D
∠BDC
顶点在圆上,且两边都和圆相交的角叫做圆周角。
下列各图中的角是圆周角的是 (填序号)。
⑤
80°
②延长AO交⊙O于点C,连结CB,
求∠C的度数。
40°
如图,在⊙O中,∠AOB=80°
①求 AB 的度数;
等腰三角形顶角的外角度数=2×底角的度数
O
A
B
C
.
圆心角:顶点在圆心的角,两边都和圆相交的角
圆周角:顶点在圆上,两边都和圆相交的角
同弧所对的圆心角与圆周角有何关系?
大胆猜想:
∠BOC=2∠BAC
同弧所对的圆周角度数=×同弧所对的圆心角度数.
.
.
∠BOC=∠BAC
.
证明:(1)当圆心O在圆周角∠BAC的一边AB上时
特殊:圆心O落在圆周角的边上!!
已知: 如图,∠BOC和∠BAC分别是 BC 所对的圆心角和圆周角
求证: ∠BAC= ∠BOC
圆周角的度数等于它所对弧上的圆心角度数的一半
∵OA=OB
∴∠A=∠ABO
∵∠BOC是△OAB的外角
∴∠BOC=∠A+∠ABO=2∠BAC
∴ ∠BAC= ∠BOC
.
当圆心O在圆周角∠BAC的内部时,
已知: 如图,∠BOC和∠BAC分别是 BC 所对的圆心角和圆周角
求证: ∠BAC= ∠BOC
证明:
连接AO并延长,交⊙O于点D
由(1)得∠BAD= ∠BOD,∠DAC= ∠DOC
∴∠BAD+∠DAC= (∠BOD+∠DOC)
即∠BAC= ∠BOC
.
D
证明:
当圆心O在圆周角∠BAC的外部时
D
已知: 如图,∠BOC和∠BAC分别是 BC 所对的圆心角和圆周角
求证: ∠BAC= ∠BOC
连接AO并延长,交⊙O于点D
∠BAD= ∠BOD,∠DAC= ∠DOC
∴∠DAC-∠BAD= (∠DOC-∠BOD)
即∠BAC= ∠BOC
.
当点A在 上移动过程中是否满足这个关系式呢?
在移动过程中,∠BAC与圆心O有几种位置关系
程在移动过程中,∠BAC与圆心O有几种位置关系
中,∠BAC与圆心O有几种位置关系
①圆周角内
②圆周角外
③圆周角的一条边上
圆周角的度数等于它所对弧上的圆心角度数的一半
同弧所对圆周角相等
圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半
一条弧所对的圆周角等于它所对的圆心角的一半。
∵∠BAC和∠BOC都对BC
∴∠BAC= ∠BOC
⌒
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
直径对直角
直角对直径
如图,AB是直径,则∠ACB=__.
如图,∠ACB=90°,则AB为⊙O的__.
半圆(或直径)所对的圆周角是直角.
90°的圆周角所对的弦是直径.
A
O
C
B
900
直径
分类讨论的依据大多是在证明过程中产生重要影响的图形之间的相对位置。如圆周角定理的证明的分类依据是圆心和圆周角之间的相对位置。根据圆心在圆周角的角边、角内和角外,把证明分三种情况进行讨论。
角边上
角内
角外
例1 如图,等腰三角形ABC的顶角∠BAC为50°,以腰AB为直径作半圆,
交BC于点D,交AC于点E.
解: 连结BE,AD
∵ AB是圆的直径
∴∠AEB=∠ADB=90°(直径所对的圆周角是直角)
∵∠BAC=50°
∴∠ABE=90°-∠BAC=90°-50°=40°
又∵△ABC是等腰三角形,
∴∠ABC=∠C=
∠BAD=∠CAD=BAC=50°=25°
由圆周角定理,得BD2∠BAD=2×25°=50°
DE2∠CAD=2×25°=50°,AE=2∠ABE=2×40°=80°
新知讲解
1、圆周角的定义:
顶点在圆上,两边都与圆相交的角.
2、圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
3、圆周角定理的推论:
半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
归纳小结
1.图中有几个圆周角?( )
A.2个 B.3个 C.4个 D.5个
D
夯实基础,稳扎稳打
2.如图,在下列各图中,
∠α1=_________, ∠α2=_______, ∠α3=_________, ∠α4=________.
.O
(
(
α2
1200
.
(
(
300
α3
O
.
(
(
α1
750
O
.
(
(
1100
α4
37.5°
60°
120°
125°
3. 如图,若∠A=40°,则∠OBC= .
500
4.如图,在☉O中,∠AOC=140°,∠ACB=50°,求∠BAC的度数.
∵∠ACB=50°
∴∠AOB=100°
∴∠COB=∠AOC -∠AOB
=140°-100°
=40°
∴∠BAC=200
解:
n0
∠AOB=n0
.
6.如图,△ABC是☉O的内接三角形,AD是☉O的直径,∠ABC=50°,求∠CAD的度数.
∵∠ABC=50°
∵AD是☉O的直径
∠CAD=40°
.
7.已知:如图,OA是☉O的半径,以OA为直径的☉C与☉O的弦AB相交于点D,求证:AD=DB.
连续递推,豁然开朗
┛
证明:连接OD
∵AO是☉C的直径
AD=DB (垂径定理)
.
∠ODA=90°
.
OD⊥AB
.
8.在⊙O中,圆心角∠AOB=560,则弦AB所对的圆周角等于( )
A、280
B、1120
C、280或1520
D、1240或560
A
B
(
.O
C
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
