3.5 圆周角 (2) 课件(共23张PPT)
文档属性
| 名称 | 3.5 圆周角 (2) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 21:22:27 | ||
图片预览

文档简介
(共23张PPT)
浙教版九年级上册
3.5 圆周角 (2)
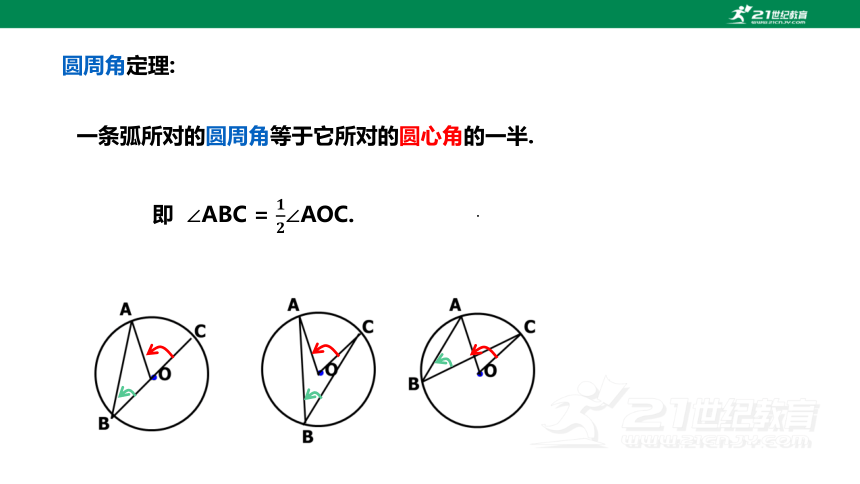
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
即 ∠ABC = ∠AOC.
.
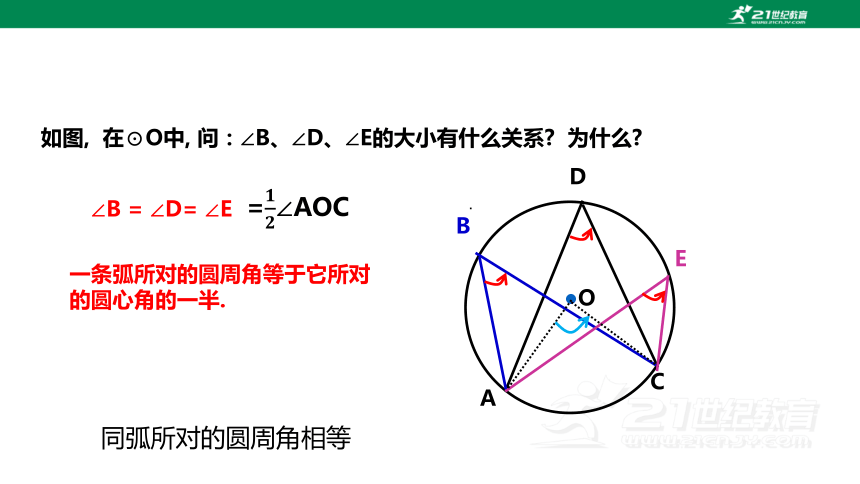
如图, 在⊙O中, 问:∠B、∠D、∠E的大小有什么关系 为什么
∠B = ∠D= ∠E
一条弧所对的圆周角等于它所对的圆心角的一半.
●O
B
A
C
D
E
=∠AOC
.
同弧所对的圆周角相等
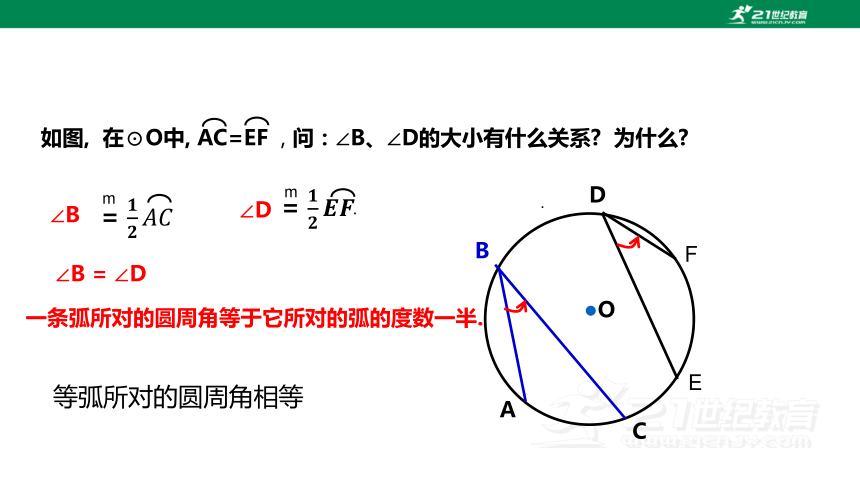
一条弧所对的圆周角等于它所对的弧的度数一半.
等弧所对的圆周角相等
●O
B
A
C
D
E
F
如图, 在⊙O中, AC=EF , 问:∠B、∠D的大小有什么关系 为什么
=
.
m
∠B
=
.
m
∠D
∠B = ∠D
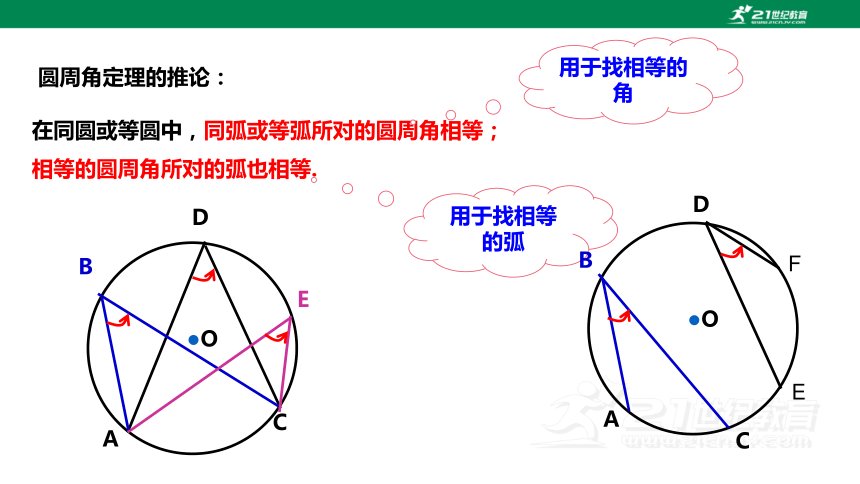
在同圆或等圆中,同弧或等弧所对的圆周角相等;
相等的圆周角所对的弧也相等.
圆周角定理的推论:
用于找相等的角
用于找相等的弧
●O
B
A
C
D
E
●O
B
A
C
D
E
F
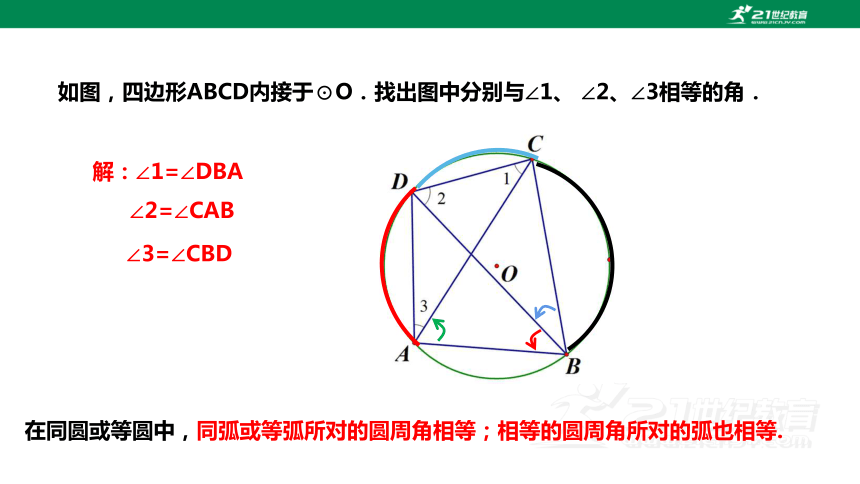
如图,四边形ABCD内接于⊙O.找出图中分别与∠1、 ∠2、∠3相等的角.
解:∠1=∠DBA
在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
∠2=∠CAB
∠3=∠CBD
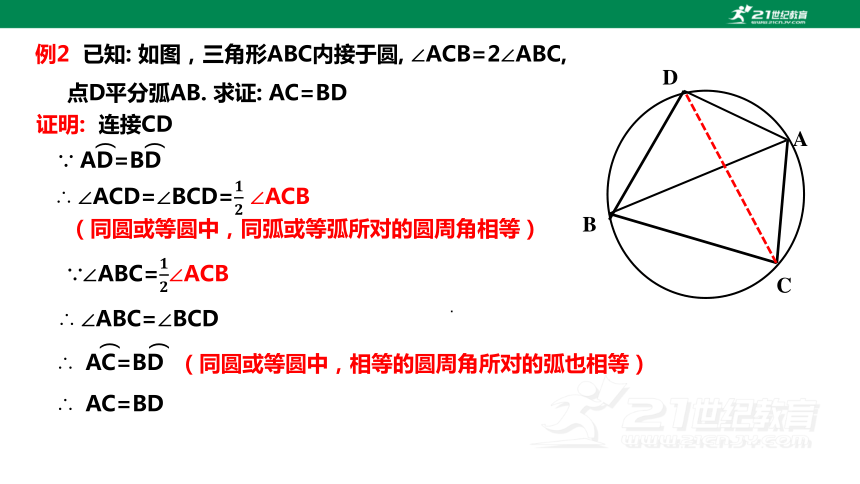
例2 已知: 如图,三角形ABC内接于圆, ∠ACB=2∠ABC,
点D平分弧AB. 求证: AC=BD
A
B
C
D
证明: 连接CD
∵ AD=BD
(
(
∴ ∠ACD=∠BCD= ∠ACB
(同圆或等圆中,同弧或等弧所对的圆周角相等)
∴ ∠ABC=∠BCD
∴ AC=BD
(
(
(同圆或等圆中,相等的圆周角所对的弧也相等)
∴ AC=BD
∵∠ABC=∠ACB
.
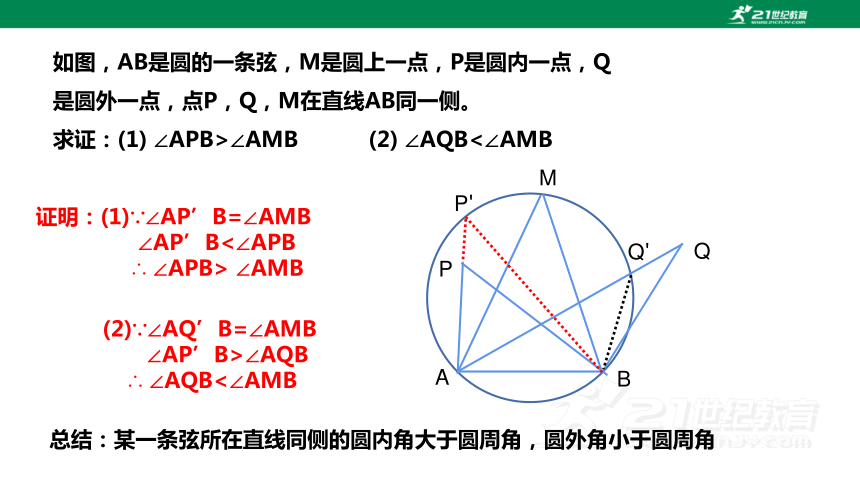
如图,AB是圆的一条弦,M是圆上一点,P是圆内一点,Q是圆外一点,点P,Q,M在直线AB同一侧。
求证:(1) ∠APB>∠AMB (2) ∠AQB<∠AMB
证明:(1)∵∠AP’B=∠AMB
∠AP’B<∠APB
∴ ∠APB> ∠AMB
(2)∵∠AQ’B=∠AMB
∠AP’B>∠AQB
∴ ∠AQB<∠AMB
总结:某一条弦所在直线同侧的圆内角大于圆周角,圆外角小于圆周角
A
B
M
P
Q
P'
Q'
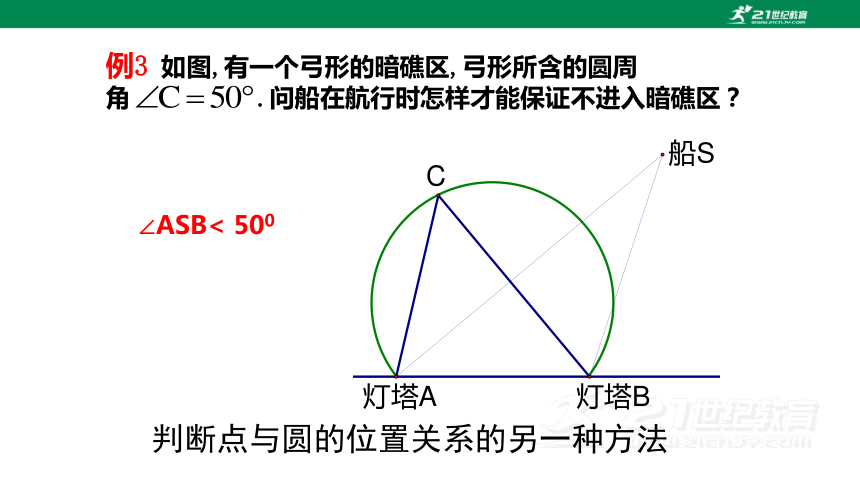
例3 如图,有一个弓形的暗礁区,弓形所含的圆周角 .问船在航行时怎样才能保证不进入暗礁区?
判断点与圆的位置关系的另一种方法
∠ASB< 500
在同圆或等圆中,如果两个圆心角、
两条弧,两条弦、两个弦心距中有一对量相等,
那么它们所对应的其余各对量都相等.
∠AOB=∠COD
AB=CD
OE=OF
.
两个圆周角
G
H
∠G=∠H
在同圆或等圆中,相等的圆周角所对的弧相等。
在同圆或等圆中,同弧或等弧所对的圆周角相等;
∠DAB=∠DCB
夯实基础,稳扎稳打
2 如图,在⊙O中,弦AB与CD交于点M,∠A=45°,
∠AMD=75°,则∠B的度数是( )
A.15° B.25°
C.30° D.75°
3 如图,在⊙O中,AB=AC ,∠AOB=40°,则∠ADC 的度数是( )
A.40° B.30°
C.20° D.15°
⌒
⌒
C
C
4.如图,△ABC内接于圆,AB=AC, 的度数为60°,
求∠B,∠C的度数.
60°
m
∵
∠A=300
∴
AB=AC
∵
∠B=∠C=(1800-300)÷2=750
∴
5.一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.
A
B
C
100
.
.
A
B
C
D
7.已知:如图,CD,AB是☉O的两条弦, ,
求证:CD∥AB
O
1
2
∵
∠1=∠2
∴
∴CD∥AB
O
3
4
8.已知:如图,在☉O中,AB=CD,求证:∠ABD=∠CDB.
证明:∵AB=CD
=
︵
AB
︵
CD
∴
∴
︵
AB
︵
AC
-
=
︵
CD
︵
AC
-
︵
AD
=
即:
︵
BC
∴∠ABD=∠CDB.
9.已知:如图,AB是☉O的直径,弦AC与半径OD平行.
求证:
3
2
4
1
.
10.如图,AB是☉O的直径,弦CD⊥AB于点E,G是任意一点,连结AD,GD,求证:∠ADC=∠AGD.
CD⊥AB
证明:∵
︵
AD
=
︵
AC
∴
∠ADC=∠AGD
∴
连续递推,豁然开朗
11.如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.
(1)求∠B的大小;(2)已知AD=6,求圆心O到BD的距离.
解:(1)∵∠CAB与∠CDB是弧BC所对的圆周角,∠CAB=40°
∴∠CAB=∠CDB=40°
又∵∠APD=65°
∴∠APD-∠CDB=∠B
即∠B=65°-40°=25°
E
┓
(2)∵AB是⊙O的直径,
∴∠ADB=90°,
过O作OE⊥BD于点E,
∵ O是AB的中点,AD=6
∴OE=AD=3
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
3.5 圆周角 (2)
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
即 ∠ABC = ∠AOC.
.
如图, 在⊙O中, 问:∠B、∠D、∠E的大小有什么关系 为什么
∠B = ∠D= ∠E
一条弧所对的圆周角等于它所对的圆心角的一半.
●O
B
A
C
D
E
=∠AOC
.
同弧所对的圆周角相等
一条弧所对的圆周角等于它所对的弧的度数一半.
等弧所对的圆周角相等
●O
B
A
C
D
E
F
如图, 在⊙O中, AC=EF , 问:∠B、∠D的大小有什么关系 为什么
=
.
m
∠B
=
.
m
∠D
∠B = ∠D
在同圆或等圆中,同弧或等弧所对的圆周角相等;
相等的圆周角所对的弧也相等.
圆周角定理的推论:
用于找相等的角
用于找相等的弧
●O
B
A
C
D
E
●O
B
A
C
D
E
F
如图,四边形ABCD内接于⊙O.找出图中分别与∠1、 ∠2、∠3相等的角.
解:∠1=∠DBA
在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
∠2=∠CAB
∠3=∠CBD
例2 已知: 如图,三角形ABC内接于圆, ∠ACB=2∠ABC,
点D平分弧AB. 求证: AC=BD
A
B
C
D
证明: 连接CD
∵ AD=BD
(
(
∴ ∠ACD=∠BCD= ∠ACB
(同圆或等圆中,同弧或等弧所对的圆周角相等)
∴ ∠ABC=∠BCD
∴ AC=BD
(
(
(同圆或等圆中,相等的圆周角所对的弧也相等)
∴ AC=BD
∵∠ABC=∠ACB
.
如图,AB是圆的一条弦,M是圆上一点,P是圆内一点,Q是圆外一点,点P,Q,M在直线AB同一侧。
求证:(1) ∠APB>∠AMB (2) ∠AQB<∠AMB
证明:(1)∵∠AP’B=∠AMB
∠AP’B<∠APB
∴ ∠APB> ∠AMB
(2)∵∠AQ’B=∠AMB
∠AP’B>∠AQB
∴ ∠AQB<∠AMB
总结:某一条弦所在直线同侧的圆内角大于圆周角,圆外角小于圆周角
A
B
M
P
Q
P'
Q'
例3 如图,有一个弓形的暗礁区,弓形所含的圆周角 .问船在航行时怎样才能保证不进入暗礁区?
判断点与圆的位置关系的另一种方法
∠ASB< 500
在同圆或等圆中,如果两个圆心角、
两条弧,两条弦、两个弦心距中有一对量相等,
那么它们所对应的其余各对量都相等.
∠AOB=∠COD
AB=CD
OE=OF
.
两个圆周角
G
H
∠G=∠H
在同圆或等圆中,相等的圆周角所对的弧相等。
在同圆或等圆中,同弧或等弧所对的圆周角相等;
∠DAB=∠DCB
夯实基础,稳扎稳打
2 如图,在⊙O中,弦AB与CD交于点M,∠A=45°,
∠AMD=75°,则∠B的度数是( )
A.15° B.25°
C.30° D.75°
3 如图,在⊙O中,AB=AC ,∠AOB=40°,则∠ADC 的度数是( )
A.40° B.30°
C.20° D.15°
⌒
⌒
C
C
4.如图,△ABC内接于圆,AB=AC, 的度数为60°,
求∠B,∠C的度数.
60°
m
∵
∠A=300
∴
AB=AC
∵
∠B=∠C=(1800-300)÷2=750
∴
5.一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.
A
B
C
100
.
.
A
B
C
D
7.已知:如图,CD,AB是☉O的两条弦, ,
求证:CD∥AB
O
1
2
∵
∠1=∠2
∴
∴CD∥AB
O
3
4
8.已知:如图,在☉O中,AB=CD,求证:∠ABD=∠CDB.
证明:∵AB=CD
=
︵
AB
︵
CD
∴
∴
︵
AB
︵
AC
-
=
︵
CD
︵
AC
-
︵
AD
=
即:
︵
BC
∴∠ABD=∠CDB.
9.已知:如图,AB是☉O的直径,弦AC与半径OD平行.
求证:
3
2
4
1
.
10.如图,AB是☉O的直径,弦CD⊥AB于点E,G是任意一点,连结AD,GD,求证:∠ADC=∠AGD.
CD⊥AB
证明:∵
︵
AD
=
︵
AC
∴
∠ADC=∠AGD
∴
连续递推,豁然开朗
11.如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.
(1)求∠B的大小;(2)已知AD=6,求圆心O到BD的距离.
解:(1)∵∠CAB与∠CDB是弧BC所对的圆周角,∠CAB=40°
∴∠CAB=∠CDB=40°
又∵∠APD=65°
∴∠APD-∠CDB=∠B
即∠B=65°-40°=25°
E
┓
(2)∵AB是⊙O的直径,
∴∠ADB=90°,
过O作OE⊥BD于点E,
∵ O是AB的中点,AD=6
∴OE=AD=3
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
