浙教版八年级上册 5.3 一次函数 课件(共14张PPT)
文档属性
| 名称 | 浙教版八年级上册 5.3 一次函数 课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
正比例函数的解析式是怎样的?
一次函数的解析式是怎样的?
y=kx
(k为常数,且k≠0)
y=kx+b
(k、b为常数,且k≠0)
当b=0时,
一次函数y=kx+b就变形为
特殊的一次函数——正比例函数y=kx
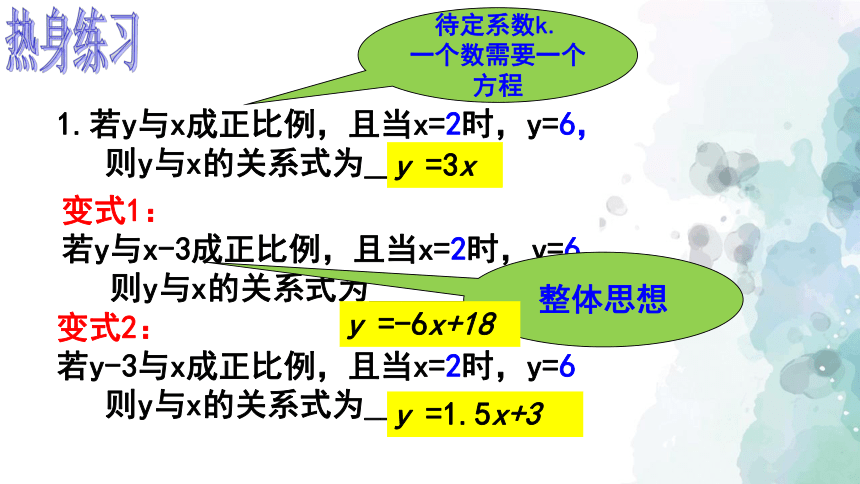
1.若y与x成正比例,且当x=2时,y=6,
则y与x的关系式为_______
变式1:
若y与x-3成正比例,且当x=2时,y=6
则y与x的关系式为_______
变式2:
若y-3与x成正比例,且当x=2时,y=6
则y与x的关系式为_______
待定系数k.
一个数需要一个方程
整体思想
y =3x
y =-6x+18
y =1.5x+3
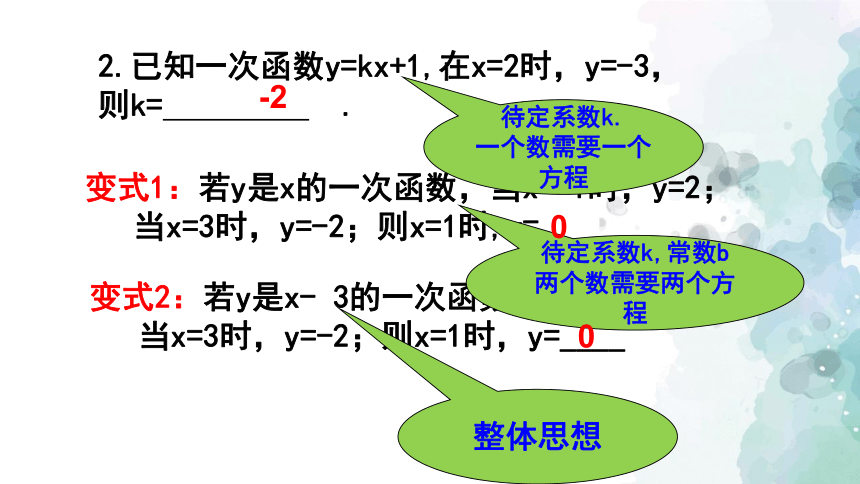
2.已知一次函数y=kx+1,在x=2时,y=-3,
则k= .
变式1:若y是x的一次函数,当x=-1时,y=2;
当x=3时,y=-2;则x=1时,y=____
-2
变式2:若y是x- 3的一次函数,当x=-1时,y=2;
当x=3时,y=-2;则x=1时,y=____
待定系数k.
一个数需要一个方程
整体思想
待定系数k,常数b
两个数需要两个方程
0
0
例3
已知y是x的一次函数,当x=3时,y=1;当x=-2时,
y=-14.求这个一次函数的表达式.
解 因为y是x的一次函数,所以可设所求表达式为y=kx+b (k≠0).
将x=3,y=1和x=-2,y=-14分别代入上式,得
解这个方程组,得
所以所求的一次函数表达式为y=3x -8.
用待定系数法求一次函数表达式的步骤
1.设所求的一次函数表达式为y=kx + b,其中k,b是待确定的常数,k≠0.
4.把求得的k,b的值代入y=kx+b,就得到所求的一次函数表达式.
3.解这个关于k,b的二元一次方程组,求出k,b的值.
2.把两对已知的自变量与函数的对应值分别代入y=kx+b,得到关于k,b的二元一次方程组.
解:
植树造林
(1)可选用什么数学方法来描述该地区的森林面积的变化
(2)如果该地区坚持植树造林,森林面积每年按相同的速度增长,那么到2025年底,该地区的森林面积将增加到多少万公顷
例4、为了的改善生态环境,某地区大力开展植树造林活动。从2010年底开始,森林面积几乎每年以相同的速度增长。据有关报道,到2018年底,该地区的森林面积已从2015年底的65.6万公顷扩展到67.7万公顷。
问:(1)可选用什么数学方法来描述该地区的森林面积的变化
分析:①森林面积是如何变化的?
②森林面积的变化与哪些量有关?
③这些量中哪些是常量?哪些是变量?
(常量:相同的速度; 2015、2018年底的森林面积。变量:森林面积随着时间的变化而不断扩大。)
④如果森林面积的增长速度为k万公顷/年,那么经x年增加了多少万公顷?
⑤也就是说可选用一次函数来描述森林面积的变化.
⑥要求出k和b,关键能否建立关于这两个常数的二元一次方程组.
练一练
解:设行李票费用y关于行李质量x的函数表达式为:y=kx+b.
所以y关于x的函数表达式为y=1.5x -15.
某航空公司规定旅客可免费托运一定质量的行李,超过规定质量的行李需买行李票,行李票费用y(元)是行李质量x(kg)的一次函数.已知当行李的质量分别为20kg,40kg时,需支付的行李票费用为15元和45元.求y关于x的函数表达式.
15=20k+b,
45=40k+b,
k=1.5,
解这个方程组,得
b= -15.
1、用待定系数法求函数表达式;
2、步骤:①设;②代;③解;④回归.
3、数学方法或思想:
待定系数法;
数学建模;
转化思想;
整体思想。
说明:如果y是x的一次函数,那么先设y=kx+b,再用待定系数法;对于没有指明是哪一类函数,应首先分析数量关系,明确是何种函数后,再设表达式。
小 结
成功不是一朝一夕的,
它是一个逐步积累的过程,
希望在任何时刻都不要轻言放弃。
金玉良言
正比例函数的解析式是怎样的?
一次函数的解析式是怎样的?
y=kx
(k为常数,且k≠0)
y=kx+b
(k、b为常数,且k≠0)
当b=0时,
一次函数y=kx+b就变形为
特殊的一次函数——正比例函数y=kx
1.若y与x成正比例,且当x=2时,y=6,
则y与x的关系式为_______
变式1:
若y与x-3成正比例,且当x=2时,y=6
则y与x的关系式为_______
变式2:
若y-3与x成正比例,且当x=2时,y=6
则y与x的关系式为_______
待定系数k.
一个数需要一个方程
整体思想
y =3x
y =-6x+18
y =1.5x+3
2.已知一次函数y=kx+1,在x=2时,y=-3,
则k= .
变式1:若y是x的一次函数,当x=-1时,y=2;
当x=3时,y=-2;则x=1时,y=____
-2
变式2:若y是x- 3的一次函数,当x=-1时,y=2;
当x=3时,y=-2;则x=1时,y=____
待定系数k.
一个数需要一个方程
整体思想
待定系数k,常数b
两个数需要两个方程
0
0
例3
已知y是x的一次函数,当x=3时,y=1;当x=-2时,
y=-14.求这个一次函数的表达式.
解 因为y是x的一次函数,所以可设所求表达式为y=kx+b (k≠0).
将x=3,y=1和x=-2,y=-14分别代入上式,得
解这个方程组,得
所以所求的一次函数表达式为y=3x -8.
用待定系数法求一次函数表达式的步骤
1.设所求的一次函数表达式为y=kx + b,其中k,b是待确定的常数,k≠0.
4.把求得的k,b的值代入y=kx+b,就得到所求的一次函数表达式.
3.解这个关于k,b的二元一次方程组,求出k,b的值.
2.把两对已知的自变量与函数的对应值分别代入y=kx+b,得到关于k,b的二元一次方程组.
解:
植树造林
(1)可选用什么数学方法来描述该地区的森林面积的变化
(2)如果该地区坚持植树造林,森林面积每年按相同的速度增长,那么到2025年底,该地区的森林面积将增加到多少万公顷
例4、为了的改善生态环境,某地区大力开展植树造林活动。从2010年底开始,森林面积几乎每年以相同的速度增长。据有关报道,到2018年底,该地区的森林面积已从2015年底的65.6万公顷扩展到67.7万公顷。
问:(1)可选用什么数学方法来描述该地区的森林面积的变化
分析:①森林面积是如何变化的?
②森林面积的变化与哪些量有关?
③这些量中哪些是常量?哪些是变量?
(常量:相同的速度; 2015、2018年底的森林面积。变量:森林面积随着时间的变化而不断扩大。)
④如果森林面积的增长速度为k万公顷/年,那么经x年增加了多少万公顷?
⑤也就是说可选用一次函数来描述森林面积的变化.
⑥要求出k和b,关键能否建立关于这两个常数的二元一次方程组.
练一练
解:设行李票费用y关于行李质量x的函数表达式为:y=kx+b.
所以y关于x的函数表达式为y=1.5x -15.
某航空公司规定旅客可免费托运一定质量的行李,超过规定质量的行李需买行李票,行李票费用y(元)是行李质量x(kg)的一次函数.已知当行李的质量分别为20kg,40kg时,需支付的行李票费用为15元和45元.求y关于x的函数表达式.
15=20k+b,
45=40k+b,
k=1.5,
解这个方程组,得
b= -15.
1、用待定系数法求函数表达式;
2、步骤:①设;②代;③解;④回归.
3、数学方法或思想:
待定系数法;
数学建模;
转化思想;
整体思想。
说明:如果y是x的一次函数,那么先设y=kx+b,再用待定系数法;对于没有指明是哪一类函数,应首先分析数量关系,明确是何种函数后,再设表达式。
小 结
成功不是一朝一夕的,
它是一个逐步积累的过程,
希望在任何时刻都不要轻言放弃。
金玉良言
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
