浙教版数学八年级上册 5.2函数第1课时函数的概念 课件(共24张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 5.2函数第1课时函数的概念 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 878.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-31 08:50:56 | ||
图片预览








文档简介
(共24张PPT)
第5章 一次函数
5.2 函数
第1课时 函数的概念
学习目标
了解函数的三种表示方法:解析法、列表法、图象法.
了解函数的相关概念.
会求函数值,并能说明函数值的实际意义.
情景引入
根据经验,跳远的距离 s=0.085v2 ( v 是助跑的速度,0<v<10.5米/秒).
其中变量 s 随着哪一个量的变化而变化?
变量 s 随着助跑的速度v的变化而变化.
复习回顾
如果小亮骑自行车去公园,以每分钟6米的速度匀速行驶.
(1) 在小亮骑车去公园的过程中有哪些量?
(2) 在上述量中,哪些是变量,哪些是常量?
(3) 说说小亮骑1分钟、2分钟、t分钟的路程是多少?
(4) 写出路程s和时间t的关系式.
路程,时间,速度.
路程、时间是变量,速度是常量.
S1=6米,S2=12米,St=6t.
S=6t
合作探究
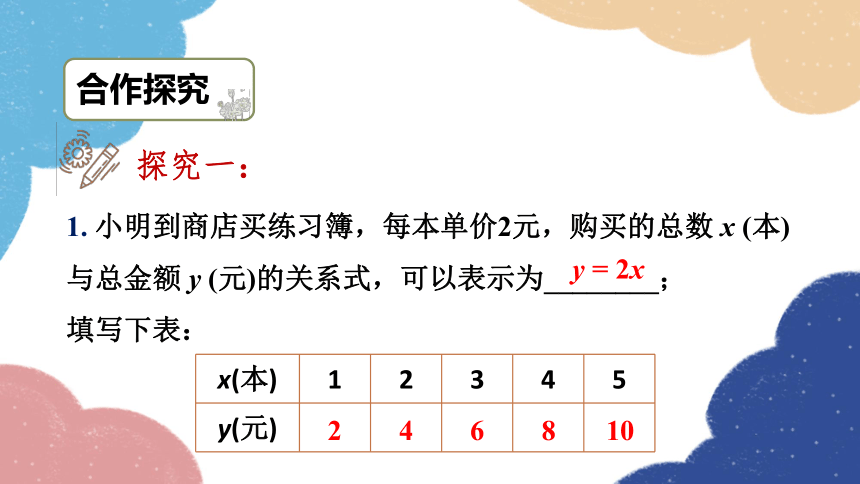
1. 小明到商店买练习簿,每本单价2元,购买的总数 x (本)与总金额 y (元)的关系式,可以表示为________;
填写下表:
y = 2x
x(本) 1 2 3 4 5
y(元)
2
4
6
8
10
探究一:
合作探究
2. 圆的周长 C 与半径 r 的关系式为________;
填写下表:
C = 2πr
半径 r 1 2 3 4 5
圆周长C
2π
4π
6π
8π
10π
问题1和问题2所列出的关系式有什么共同特点?
都有两个变量,给定其中某一个变量的值,相应地就确定了另一个变量的值.
函数的概念
一般地,在某个变化过程中,设有两个变量 x 和 y ,如果对于变量 x 的每一个确定的值, y 都有唯一确定的值,那么就说 y 是 x 的函数, x 叫做自变量.
典例精讲
例1 判断下面各量之间的关系是不是函数关系,若是,请指出自变量.
(1) 长方形的一边长 b 一定时,与其相邻的另一边长 a 与周长 C ,其中 C = 2(a+b);
解:长方形的周长 C = 2(a+b),当一边长 b 一定时,与其
相邻的另一边长 a 所取的每一个确定的值,周长 C 都有唯
一的值与它对应,所以 C 是 a 的函数.
自变量是 a .
典例精讲
(2) y = |x| 中的 x 与 y;
解:在 y = |x| 中,对于每一个 x 值,y 都有唯一的值与它
对应,所以 y 是 x 的函数.
自变量是 x.
自变量是 a.
典例精讲
本题运用定义法解答.
判断一个关系是否是函数关系,根据函数定义,主要
从以下3个方面分析:
(1) 是否在一个变化过程中;
(2) 在该过程中是否有两个变量;
(3) 对于一个变量每取一个确定的值,另一个变量是
否有唯一确定的值与其对应.
合作探究
探究二:
1. 正方形的面积 S 与边长 x 的取值如下表,S 是不是 x 的函数?
这里是怎样表示正方形面积 S 与边长 x 之间的函数关系的?
列数值表来表示.
边长 x 1 2 3 4 5 6 7 …
面积 S …
1 4 9 16 25 36 49
是
合作探究
2. 城市居民用的天然气1m3收费2.88元,使用 x (m3) 天然气应缴纳的费用 y (元)为 y = 2.88x,y 是不是 x 的函数?
这里是怎样表示缴纳的天然气费用 y 与所用天然气的体积x 的函数关系的?
是
用函数关系式 y = 2.88x 来表示的.
像y = 2.88x 这种表示函数关系的等式,叫做函数表达式,简称函数式.用函数表达式表示函数的方法也叫解析法.
合作探究
用平面直角坐标系中的一个图象来表示.
3. 下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,气温 T 是不是时间 t 的函数?
这里是怎样表示气温 T 与时间 t 之间的函数关系的?
是
函数的表示
函数的三种表示法:
y = 2.88x
图象法、
列表法、
解析法.
图象法 列表法 解析法
定义
优点
通过把自变量x的一系列值和函数y的对应值列成一个表来表示函数关系的方法.
对于表中自变量的每一个值,可以清楚地找到对应值.
用函数表达式表示函数关系的方法.
准确地反映了函数与自变量的数量关系.
用图象来表示两个变量间的函数关系的方法.
直观地反映了函数随自变量的变化而变化的规律.
函数三种表示方法的区别
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为当自变量等于a时的函数值.
函数与函数值
注意:对于实际问题中,自变量的取值应使实际问题有意义.
函数表示的是两个变量间的一种关系,而函数值是一个数值.
典例精讲
例2 一个三角形的周长为 y cm,三边长分别为 7 cm,3 cm和 x cm.
(1) 求y关于x的函数表达式;
分析: ①问题中包含了哪些变量?x ,y 分别表示什么?
② x ,y 之间存在怎样的数量关系?这种数量关
系可以用什么形式给出?
解: 根据题设,可得 y = x+7+3,
即y关于x的函数表达式为 y = x+10.
典例精讲
解:当x = 5 时,y = 5+10 = 15(cm),
当x = 7 时,y = 7+10 = 17(cm);
实际意义:当第三条边是5 cm,7 cm 时,三角形的周长
分别是 15 cm和 17 cm.
例2 一个三角形的周长为 y cm,三边长分别为 7 cm,3 cm和 x cm.
求y关于x的函数表达式;
分别求 x = 5, x = 7 时的函数值,并说明它们的实际意义.
随堂练习
1. 下列曲线所表示的y与x之间关系不是函数关系的是( )
B.
C. D.
C
随堂练习
2. 已知函数 y = -x+3,当 x =______时,函数值为0.
3
3. 已知函数 y = ,当 x = -2 时,函数值 y 为______.
-8
2x+1(x≥0)
4x (x<0)
分析: 由题目知,y = 0,那么 -x+3 = 0,
解得 x = 3.
分析: ∵x = -2,-2 < 0,
∴ y = 4x = -2×4 = -8.
随堂练习
4. 填表并回答问题:
(1)对于x的每一个值,y都满足有唯一的值与之对应吗?
(2)y是x的函数吗?为什么?
x 1 4 9 16
y=±2x
2和-2
8和-8
18和-18
32和-32
不是,因为y的值不是唯一的.
不满足
课堂小结
函数的概念.
函数值.
函数的表示方法:
图象法、列表法、解析法.
本节课你学习了哪些内容?
特别提醒
对于一个函数,可能有很多函数值,自变量取不同的值,函数值可能不相等,故应说明函数值是当自变量取什么值时的函数值.
例:y = x+1.
当 x = 1 时,函数值 y = 2;当 x = 0 时,函数值 y = 1.
不能说函数 y = x+1 的函数值是2.
课堂小结
感谢观看!
第5章 一次函数
5.2 函数
第1课时 函数的概念
学习目标
了解函数的三种表示方法:解析法、列表法、图象法.
了解函数的相关概念.
会求函数值,并能说明函数值的实际意义.
情景引入
根据经验,跳远的距离 s=0.085v2 ( v 是助跑的速度,0<v<10.5米/秒).
其中变量 s 随着哪一个量的变化而变化?
变量 s 随着助跑的速度v的变化而变化.
复习回顾
如果小亮骑自行车去公园,以每分钟6米的速度匀速行驶.
(1) 在小亮骑车去公园的过程中有哪些量?
(2) 在上述量中,哪些是变量,哪些是常量?
(3) 说说小亮骑1分钟、2分钟、t分钟的路程是多少?
(4) 写出路程s和时间t的关系式.
路程,时间,速度.
路程、时间是变量,速度是常量.
S1=6米,S2=12米,St=6t.
S=6t
合作探究
1. 小明到商店买练习簿,每本单价2元,购买的总数 x (本)与总金额 y (元)的关系式,可以表示为________;
填写下表:
y = 2x
x(本) 1 2 3 4 5
y(元)
2
4
6
8
10
探究一:
合作探究
2. 圆的周长 C 与半径 r 的关系式为________;
填写下表:
C = 2πr
半径 r 1 2 3 4 5
圆周长C
2π
4π
6π
8π
10π
问题1和问题2所列出的关系式有什么共同特点?
都有两个变量,给定其中某一个变量的值,相应地就确定了另一个变量的值.
函数的概念
一般地,在某个变化过程中,设有两个变量 x 和 y ,如果对于变量 x 的每一个确定的值, y 都有唯一确定的值,那么就说 y 是 x 的函数, x 叫做自变量.
典例精讲
例1 判断下面各量之间的关系是不是函数关系,若是,请指出自变量.
(1) 长方形的一边长 b 一定时,与其相邻的另一边长 a 与周长 C ,其中 C = 2(a+b);
解:长方形的周长 C = 2(a+b),当一边长 b 一定时,与其
相邻的另一边长 a 所取的每一个确定的值,周长 C 都有唯
一的值与它对应,所以 C 是 a 的函数.
自变量是 a .
典例精讲
(2) y = |x| 中的 x 与 y;
解:在 y = |x| 中,对于每一个 x 值,y 都有唯一的值与它
对应,所以 y 是 x 的函数.
自变量是 x.
自变量是 a.
典例精讲
本题运用定义法解答.
判断一个关系是否是函数关系,根据函数定义,主要
从以下3个方面分析:
(1) 是否在一个变化过程中;
(2) 在该过程中是否有两个变量;
(3) 对于一个变量每取一个确定的值,另一个变量是
否有唯一确定的值与其对应.
合作探究
探究二:
1. 正方形的面积 S 与边长 x 的取值如下表,S 是不是 x 的函数?
这里是怎样表示正方形面积 S 与边长 x 之间的函数关系的?
列数值表来表示.
边长 x 1 2 3 4 5 6 7 …
面积 S …
1 4 9 16 25 36 49
是
合作探究
2. 城市居民用的天然气1m3收费2.88元,使用 x (m3) 天然气应缴纳的费用 y (元)为 y = 2.88x,y 是不是 x 的函数?
这里是怎样表示缴纳的天然气费用 y 与所用天然气的体积x 的函数关系的?
是
用函数关系式 y = 2.88x 来表示的.
像y = 2.88x 这种表示函数关系的等式,叫做函数表达式,简称函数式.用函数表达式表示函数的方法也叫解析法.
合作探究
用平面直角坐标系中的一个图象来表示.
3. 下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,气温 T 是不是时间 t 的函数?
这里是怎样表示气温 T 与时间 t 之间的函数关系的?
是
函数的表示
函数的三种表示法:
y = 2.88x
图象法、
列表法、
解析法.
图象法 列表法 解析法
定义
优点
通过把自变量x的一系列值和函数y的对应值列成一个表来表示函数关系的方法.
对于表中自变量的每一个值,可以清楚地找到对应值.
用函数表达式表示函数关系的方法.
准确地反映了函数与自变量的数量关系.
用图象来表示两个变量间的函数关系的方法.
直观地反映了函数随自变量的变化而变化的规律.
函数三种表示方法的区别
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为当自变量等于a时的函数值.
函数与函数值
注意:对于实际问题中,自变量的取值应使实际问题有意义.
函数表示的是两个变量间的一种关系,而函数值是一个数值.
典例精讲
例2 一个三角形的周长为 y cm,三边长分别为 7 cm,3 cm和 x cm.
(1) 求y关于x的函数表达式;
分析: ①问题中包含了哪些变量?x ,y 分别表示什么?
② x ,y 之间存在怎样的数量关系?这种数量关
系可以用什么形式给出?
解: 根据题设,可得 y = x+7+3,
即y关于x的函数表达式为 y = x+10.
典例精讲
解:当x = 5 时,y = 5+10 = 15(cm),
当x = 7 时,y = 7+10 = 17(cm);
实际意义:当第三条边是5 cm,7 cm 时,三角形的周长
分别是 15 cm和 17 cm.
例2 一个三角形的周长为 y cm,三边长分别为 7 cm,3 cm和 x cm.
求y关于x的函数表达式;
分别求 x = 5, x = 7 时的函数值,并说明它们的实际意义.
随堂练习
1. 下列曲线所表示的y与x之间关系不是函数关系的是( )
B.
C. D.
C
随堂练习
2. 已知函数 y = -x+3,当 x =______时,函数值为0.
3
3. 已知函数 y = ,当 x = -2 时,函数值 y 为______.
-8
2x+1(x≥0)
4x (x<0)
分析: 由题目知,y = 0,那么 -x+3 = 0,
解得 x = 3.
分析: ∵x = -2,-2 < 0,
∴ y = 4x = -2×4 = -8.
随堂练习
4. 填表并回答问题:
(1)对于x的每一个值,y都满足有唯一的值与之对应吗?
(2)y是x的函数吗?为什么?
x 1 4 9 16
y=±2x
2和-2
8和-8
18和-18
32和-32
不是,因为y的值不是唯一的.
不满足
课堂小结
函数的概念.
函数值.
函数的表示方法:
图象法、列表法、解析法.
本节课你学习了哪些内容?
特别提醒
对于一个函数,可能有很多函数值,自变量取不同的值,函数值可能不相等,故应说明函数值是当自变量取什么值时的函数值.
例:y = x+1.
当 x = 1 时,函数值 y = 2;当 x = 0 时,函数值 y = 1.
不能说函数 y = x+1 的函数值是2.
课堂小结
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
