5.3一元一次方程应用（1）

课件22张PPT。一元一次方程的应用(一)　　　　如图是２００２年釜山亚运会会
徽．会徽的图案由主办地韩国的釜山的太
极和大海的蓝色波涛组成，表现了亚洲人
的理念和超越国境的团结力量．我们要学
习他们这种为国争光和拼搏精神并把它应
用到我们的学习中来．

以下图片是我国运动员在２００２年釜山亚运会奋勇夺冠的情形．　　１．２００２年亚运会上，我国获得１５０枚金牌．比１９９４年亚运会我国获得的金牌数的２倍少３８枚，则１９９４年我国获得 _____ 枚金牌．
　　
２．若设１９９４年我国获得的金牌数为x枚，则２００２年我国获得的金牌数可用代数式表示为＿＿＿＿＿；
列出方程为＿＿＿＿＿＿＿＿＿＿＿． 做一做２Ｘ－３８２Ｘ－３８＝１５０例1 5位老师和一群学生一起去公园，教师门票按全票价每人7元，学生只收半价。如果门票总价计206.50元，那么学生有多少人？人数×票价=总票价
学生的票价=0.5 ×教师的票价
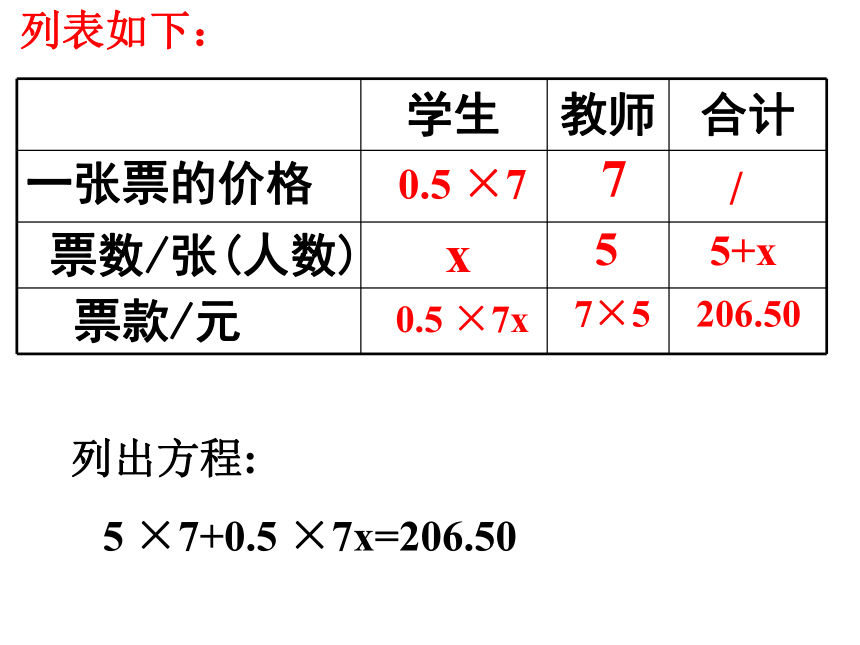
教师的总票价+学生的总票价=206.50 列出方程:
5 ×7+0.5 ×7x=206.50列表如下：0.5 ×77/x55+x0.5 ×7x7×5206.50解 设学生有x人，根据题意，得
5 ×7+0.5 ×7x=206.50解这个方程，得 x=49检验： X=49适合方程，且符合题意。答：学生有49人。运用方程解决实际问题的一般过程是：（关键是正确的找出等量关系）审题：分析题意，找出题中的数量及关系．
设元：选择一个适当的未知数用字母表示（例如x）．
列方程：根据相等关系列出方程．
解方程：求出未知数的值．
检验：检查求得的值是否正确和符合实际情形，并写出答案．1.若小明每秒跑4米，那么他5秒能跑_____米.2.小明用4分钟绕学校操场跑了两圈(每圈400米)，那么他的速度为_____米/分.3.已知小明家距离火车站1500米，他以4米/秒的速度骑车到达车站需要_____分钟.20200速度=路程÷时间时间=路程÷速度例２． 甲乙两人从ＡＢ两地同时出发，沿同一条路线相向匀速行驶．出发后经３时相遇．已知在相遇时乙比甲多行驶了９０千米，相遇后经１时乙到达Ａ地．问甲，乙行驶的速度分别是多少？分析：本题涉及路程，时间，速度三个基本数量它们之间有如下关系：1、路程＝速度×时间；2、相遇前甲行驶的路程＋９０＝相遇前 乙行驶的路程；3、相遇后乙行驶的路程＝相遇前甲行驶的路程．列出方程: 等量关系:乙相遇后路程=甲相遇前路程x333x3x+9013x列表分析如下：解 设甲行驶的速度为x千米/时,则相遇前乙行驶的路程为3x千米/时,则由题意,得解这个方程,得 x =15将x =15代入,得检验：x=15适合方程，且符合题意；答：甲行驶的速度为每小时15千米，乙行驶的速度为每小时45千米。=45变式思考（交换条件与结论）：　　甲乙两人从ＡＢ两地同时出
发，沿同一条路线相向匀速行驶
若甲的速度为１５千米／时，乙
速度为４５千米／时，在相遇时
比甲多行了９０千米，问经过多
少时间两人相遇？解：设经过x时两人相遇，由题意得：１５x＝４５x－９０
解得：x＝３
检验：x＝３适合方程，且符合题意．
答：经过３时两人相遇．小明所跑的路程小彬所跑的路程小明所跑的路程小彬所跑的路程100米相遇1、小彬和小明每天早晨坚持跑步，小明每秒跑6米，小彬每秒跑4米。(1)如果他们站在百米跑道的两端同时相向起跑，那么几秒后两人相遇？(2)如果小明站在百米跑道的起点处，小彬站在他前面10米处，两人同时同向起跑，几秒后小明能追上小彬？练习:2、三个连续奇数的和为５７，这三个数分别是＿＿＿＿＿＿＿＿3、小明以3千米/时的速度走了0.75小时，然后以一定的速度跑了0.5小时，一共前进了6千米，设小明跑步的速度为X千米/时，则由题意可列出方程为＿＿＿＿＿＿＿．4、今年父亲的年龄是儿子年龄的3倍，5年前父亲的年龄是儿子年龄的4倍，若今年儿子X岁，则今年父亲＿岁，五年前儿子＿＿岁，父亲＿＿岁，关于X的方程为＿＿＿＿＿．练习:5、从某个月的月历表中取出一个2×2方块，已知这个方块所围成的4个方格的日期之和为44，求这4个方格中的日期。6、请编一个实际应用题，要求所列的方程为15x+45x=180；练习:合作交流学了本节课你有什么收获？ 据了解，个体服装销售只要高出进价的20%便可盈利，但老板们通常以高出进价的50%——100%标价.假如你准备买一件标价为200元的服装，应在什么范围内还价？分析 还价必须高于进价的20%，老板才会将服装卖出，故应通过标价估出进货价再高出20%还价.再见