5.3一元一次方程的应用（2）

课件21张PPT。5.3一元一次方程的应用(2)运用方程解决实际问题的一般过程是: 1.审题:分析题意,找出题中的数量及其关系;3.列方程:根据相等关系列出方程;4.解方程:求出未知数的值;5.检验:检查求得的值是否正确和符合实际 情形,并写出答案. 2.设元:选择一个适当的未知数用字母表示
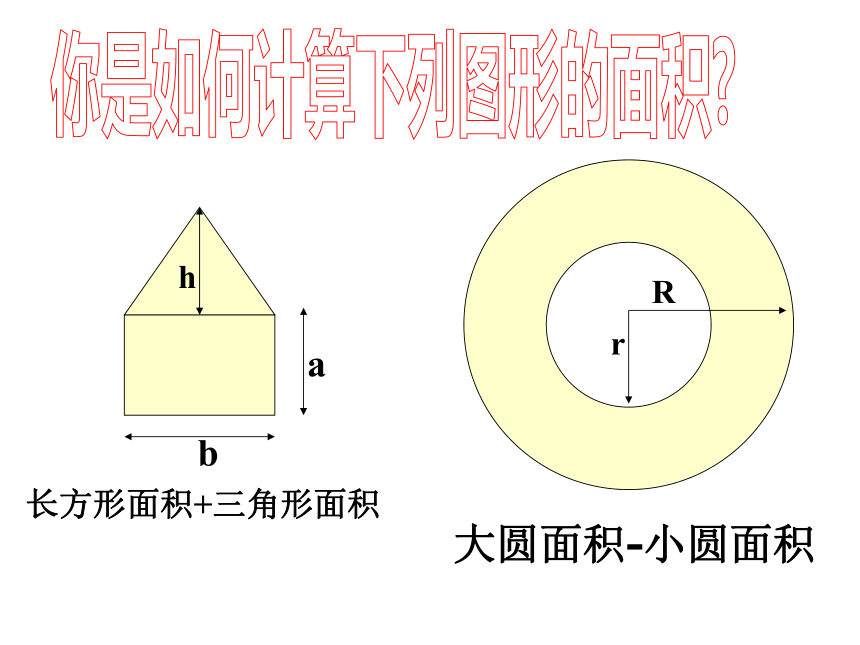
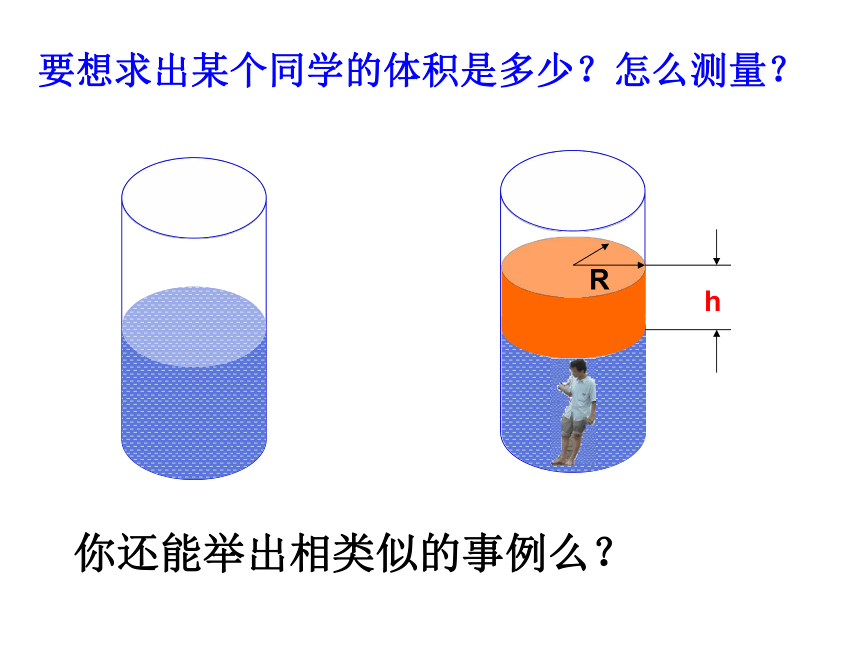
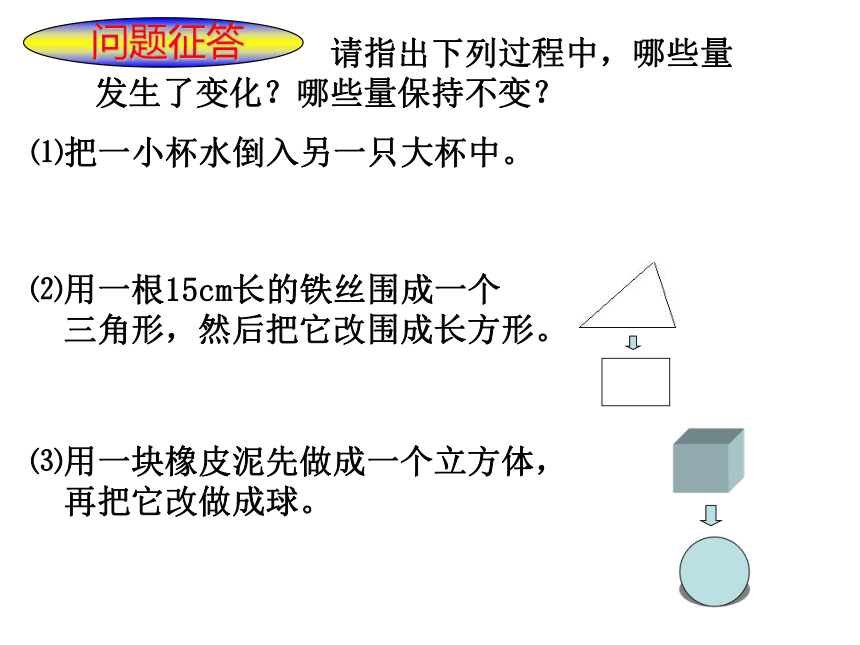
( 例如 ) ;你是如何计算下列图形的面积?abhrR长方形面积+三角形面积大圆面积-小圆面积BBhR要想求出某个同学的体积是多少？怎么测量？你还能举出相类似的事例么？ 问题征答　　　　　　　请指出下列过程中，哪些量发生了变化？哪些量保持不变？⑴把一小杯水倒入另一只大杯中。⑵用一根15cm长的铁丝围成一个
　三角形，然后把它改围成长方形。⑶用一块橡皮泥先做成一个立方体，
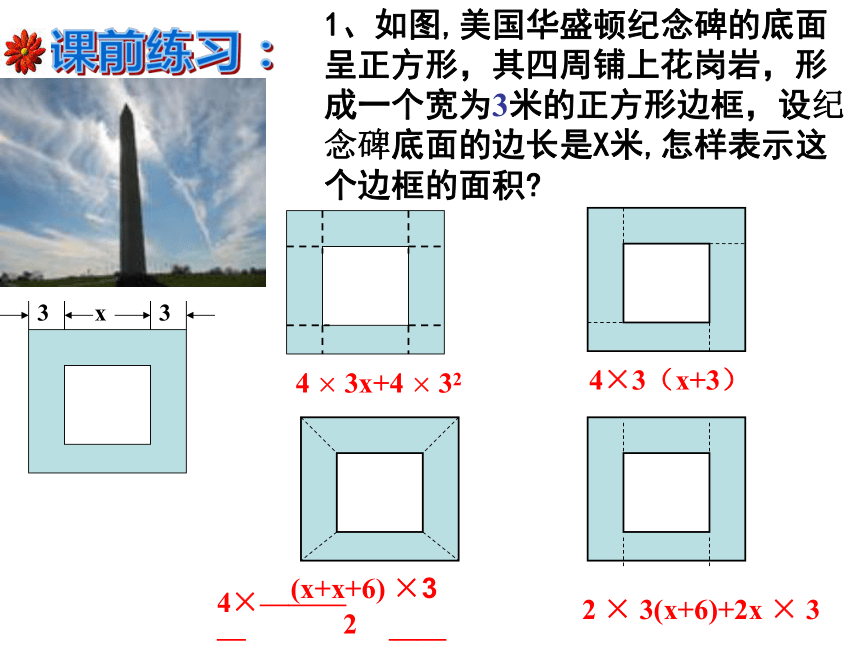
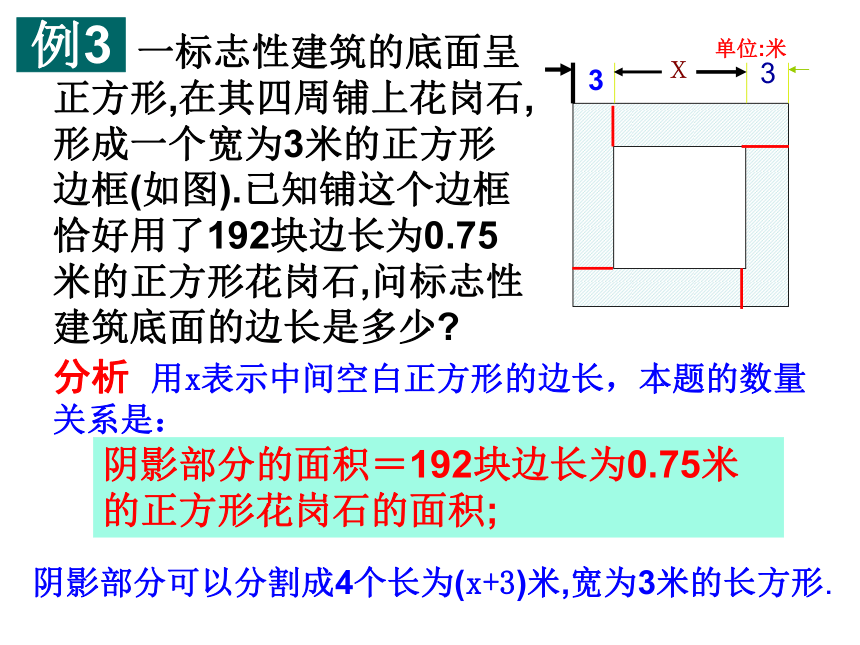
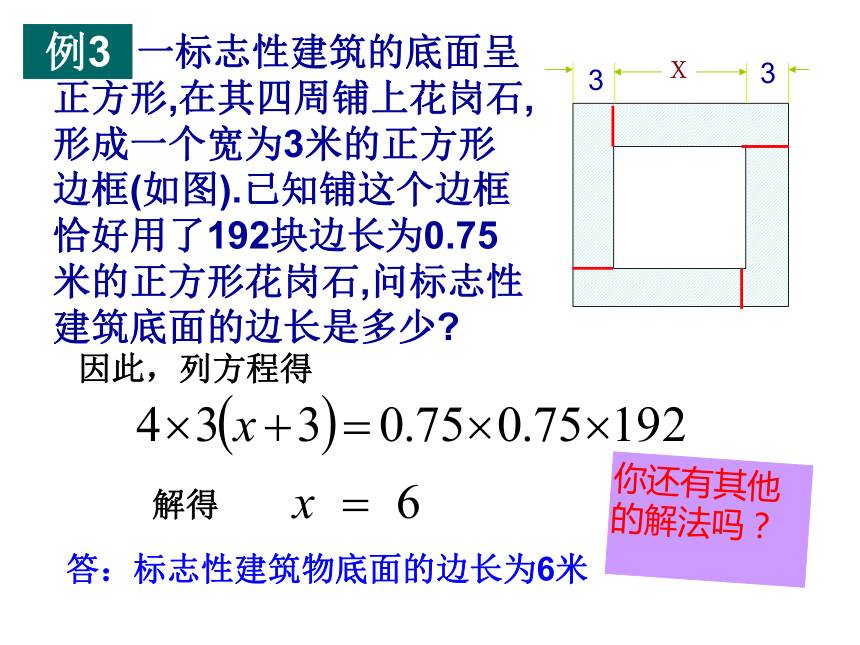
　再把它改做成球。1、如图,美国华盛顿纪念碑的底面呈正方形，其四周铺上花岗岩，形成一个宽为3米的正方形边框，设纪念碑底面的边长是X米,怎样表示这个边框的面积?课前练习：4 × 3x+4 × 324×3（x+3）2 × 3(x+6)+2x × 3例3 一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个宽为3米的正方形边框(如图).已知铺这个边框恰好用了192块边长为0.75米的正方形花岗石,问标志性建筑底面的边长是多少?单位:米x分析 用x表示中间空白正方形的边长，本题的数量关系是：阴影部分的面积＝192块边长为0.75米的正方形花岗石的面积;阴影部分可以分割成4个长为(x+3)米,宽为3米的长方形.例3 一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个宽为3米的正方形边框(如图).已知铺这个边框恰好用了192块边长为0.75米的正方形花岗石,问标志性建筑底面的边长是多少?x 因此，列方程得
解得你还有其他的解法吗？答：标志性建筑物底面的边长为6米 xx建筑物的面积=
大正方形的面积-小正方形的面积则列出方程为注意：解题中的检验对确保答案的正确和合理很有帮助，但具体过程可以省略不写。变式1、一标志性建筑的底面是边长为6米正方形，在其四周铺上花岗石，形成一个宽为3米的正方形边框，已知铺上这个边框恰好用了192块正方形花岗石，问每块正方形花岗石边长是多少米？6变式2、一标志性建筑的底面宽为6米的正方形，在其四周铺上花岗石，形成一个宽为3米的正方形边框，已知铺上这个边框恰好用了x块边长为0.75米的正方形花岗石，求X是多少?6例4 .学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人.现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲,乙两处各多少人?17+20-x23+x20-xx2317分析 设应调往甲处x人,题目中所涉及的有关数量及其关系可以用右表表示:甲处增加后人数=2×乙处增加后人数想一想：如果调往乙处的人数为x，方程应怎样列?23+20-x20-xx231717+x若设调往乙处的人数为x，方程又应怎样列? 在解决实际问题时,我们一般可以通过分析实际问题, 抽象出数学问题, 然后运用数学思想方法解决问题.用列表分析数量关系是常用的方法.2.一书架能放厚为6.3cm 的书45本.现在准备放厚为2.1cm 的书,问能放这种书多少 本?练一练1.用直径为200厘米的钢柱锻造一块长、宽、高分别为300厘米，300厘米，80厘米的长方体毛坯底板，应截取圆柱多少长？（圆柱的体积=底面积×高。计算时，π取3.14，要求结果误差不超过1厘米） 在等积变形的题目中，要抓住体积不变的等量关系。
注意：（1）圆柱的体积公式
（2）制造零件，在选材时要用进一法。3、我国古代四大发明之一的黑火药,它所用原料有硝酸钾、硫酸、木炭，它们的重量比是15：2：3，要配制这种火药320千克，三种原料应取 千克？4、在甲处工作的有272人，在乙处工作的有196人，如果要使甲处工作的人数是乙处工作的人数的3倍，应从乙处调多少人到甲处？若设应从乙处调x人到甲处，则方程可列为 。练一练应这样设未知数呢？272+x=3（196-x）5.按图示的方法搭1个三角形需要3根火柴棒,搭2个三角形需要5根火柴棒.设共搭成n 个三角形,你怎样用关于是 n 的代数式表示n 个三角形需要火柴棒的根数? 现有2009根火柴棒,能搭几个这样的三角形? 2100根呢?练一练合作交流学了本节课你有什么收获？课外拓展：1、今有四个数，取其三个相加，其和分别为22，24，27，和20，求此四个数。解：设四个数的和为x，则此四个数分别为（x-22），（x-24），（x-27），（x-20），列方程得：X= （x-22）+（x-24）+（x-27）+（x-20） 解得，x=312、某商场经销一种商品，由于进货时价格比原进价降低了6.4%，使得利润增加了8个百分点，求经销这种商品原来的利润率。设原进价为x元，销售价为y元，则：解得y=1.17x3、从甲地到乙地，先下山后走平路，某人骑自行车从甲地以每小时12千米的速度下山，而以每小时9千米的速度通过平路，到乙地用了55分钟，他回来时以每小时8千米的速度通过平路，而以每小时4千米的速度上山，回到甲地用了1.5小时，求甲、乙两地的距离。课外拓展：解：设山路长为x千米，则解得：x=3再见