浙教版数学九年级上册1.2二次函数的图象(2)教案 (表格式)
文档属性
| 名称 | 浙教版数学九年级上册1.2二次函数的图象(2)教案 (表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 230.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-01 00:00:00 | ||
图片预览


文档简介
1.2二次函数的图象(2)教案
课题 1.2二次函数的图象(2) 单元 一 学科 数学 年级 九年级(上)
学习 目标 1.学会观察、归纳、概括函数图像的特征 2. 掌握y=ax2图象的位置关系及有关性质
重点 掌握二次函数y=a(x+m)2+k(a≠0)型的图象及其特征;
难点 二次函数的性质及二次函数的平移运用数形结合思想.
教学过程
教学环节 教师活动 学生活动 设计意图
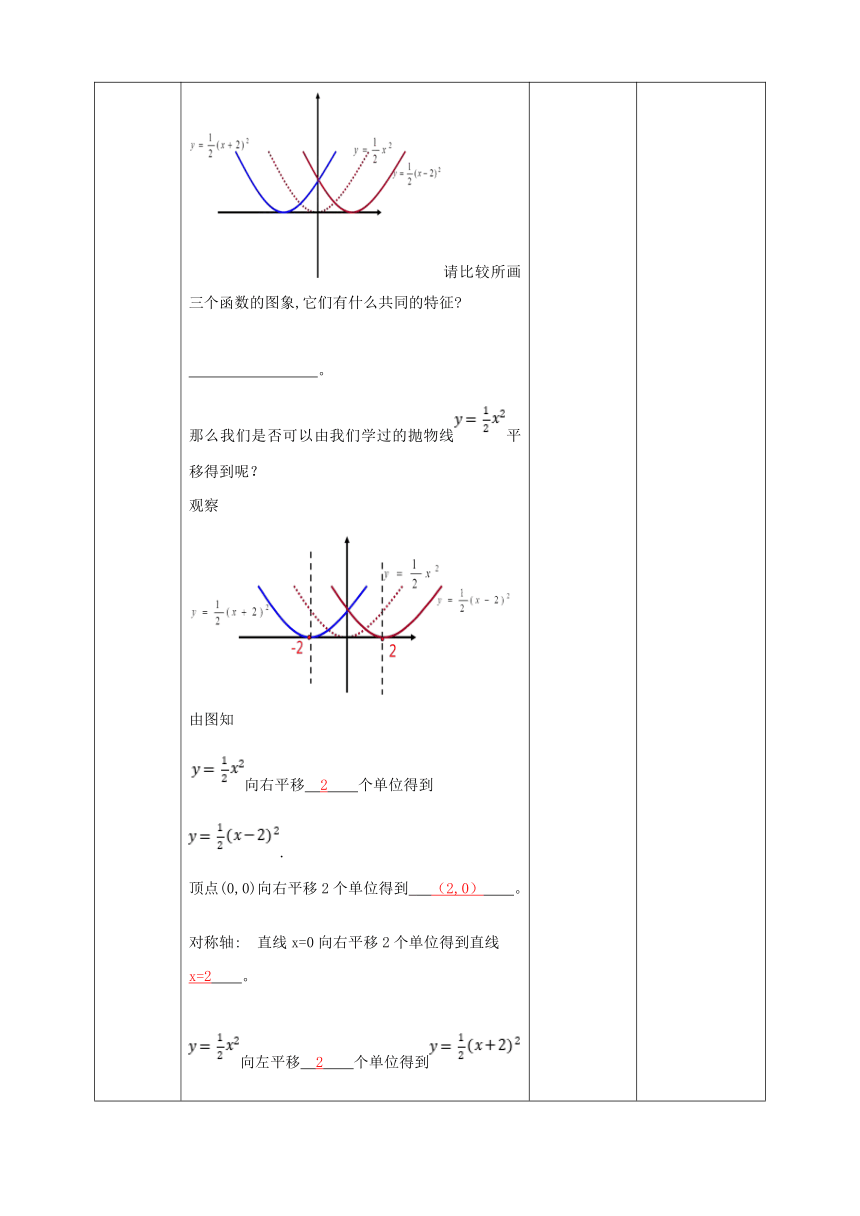
导入新课 一、创设情景,引出课题 思考:二次函数y=ax 的图象及其特点? 二次函数y=a(x-m)2的图象与二次函数y=ax2的图象开口方向、对称轴和顶点坐标是否相同 那么 y=a(x-m)2+k的图象呢? 我们开始一起去研究! 试一试:在同一坐标系中作出下列二次函数: , 填表 描点画图 请比较所画三个函数的图象,它们有什么共同的特征 。 那么我们是否可以由我们学过的抛物线平移得到呢? 观察 由图知 向右平移 2 个单位得到. 顶点(0,0)向右平移2个单位得到 (2,0) 。 对称轴: 直线x=0向右平移2个单位得到直线 x=2 。 向左平移 2 个单位得到 顶点(0,0)向左平移2个单位得到 (-2,0) 。 对称轴: 直线x=0向左平移2个单位得到 x=-2 。 思考 自议 由抛物线y=ax2(a≠0)向左(m>0)平移|m|个单位,则得y=a(x+m)2(a≠0);由抛物线y=ax2(a≠0)向右(m<0)平移|m|个单位,则得y=a(x+m)2(a≠0). (1)已知抛物线的顶点坐标求解析式通常用y=a(x+m)2+k(a≠0)的形式,称为顶点式; (2)利用草图对求平移后的抛物线常常有所帮助.
讲授新课 提炼概念 总结:二次函数y=a(x- m)2的图象和性质. (
当
m<0
时
,
向左平移
)平移: (
当
m<0
时
,
向右平移
) y=a(x- m)2 a>0时,开口________, 最 ____ 点是顶点; a<0时,开口________, 最 ____ 点是顶点; 对称轴是 _____________, 顶点坐标是 __________。(向上,低;向下,高;直线x=m,(m,0) 三、典例精讲 例2 对于二次函数请回答下列问题 把函数的图象作怎样的平移变换,就能得到函数 的图象。 (2)说出函数的图象的顶点坐标和对称轴。 解:(1)函数的图象向右平移4个单位,就得到函数 的图象。 函数的图象的顶点坐标是(4,0),对称轴是直线x=4. 试一试: 用描点法在同一直角坐标系中画出下列函数的图象: 想一想 函数由函数的图象怎样平移得到的? 函数由函数的图象怎样平移得到的? 归纳性质: 一般地函数y=a(x+m)2+k的图象,函数y=ax2的图象只是位置不同, (1)可以由y=ax2的图象先向右(当m<0)或向左(当m>0)平移∣m∣个单位,再向上(当k>0)或向下(当k<0)平移∣k∣个单位得到, (2)顶点坐标是(-m,k),对称轴是直线x=-m, (3)图象在x轴的上方还是下方,开口方向向上还是向下等性质由y=ax2来决定的。 已知抛物线的顶点坐标,常设抛物线的顶点式y=a(x+m)2+k(a≠0). 解此类题可以将不同形式的解析式统一为y=a(x+m)2+k的形式,便于解答.
课堂检测 四、巩固训练 1.将抛物线y=2x2向上平移3个单位,再向右平移2个单位,所得到的抛物线为( ) A.y=2(x+2)2+3 B.y=2(x-2)2+3 C.y=2(x-2)2-3 D.y=2(x+2)2-3 B 填写下表: 解: 向下y轴(0,0)向上y轴(0,5)向下直线x=-4(-4,0)向上直线x=-2(-2,-7)
3.(1)将如图所示的图象向左平移2个单位,写出平移后的抛物线表达式; (2)将如图所示的图象向右平移3个单位,写出平移后抛物线的表达式. 解:向左平移2个单位的图象如图中y1;向右平移3个单位的图象,如图中y2. ∵原抛物线顶点为点(0,0)且过点(3,2), ∴设其表达式为y=ax2(a≠0), 且2=a×32. ∴a=,∴y=x2. (1)向左平移2个单位后:y=(x+2)2; (2)向右平移3个单位后:y=(x-3)2. 4.已知函数y=(x+1)2-4. (1)指出函数图象的开口方向、对称轴和顶点坐标; (2)若将该抛物线先向右平移2个单位,再向上平移4个单位,求得到的抛物线的解析式; (3)原抛物线经过怎样的平移后顶点在原点? 解:(1)顶点(-1,-4),开口向上,对称轴为直线x=-1; (2)y=(x-1)2; (3)y=(x+1)2-4向右平移1个单位,再向上平移4个单位.
课堂小结 1.二次函数y=a(x+m)2(a≠0)型的图象及其特征 平移:(1)一般地,函数y=a(x+m)2(a≠0)的图象与函数y=ax2的图象只是位置不同,它可由y=ax 的图象________________________________得到. 特征:函数y=a(x+m)2的图象的顶点坐标是_______,对称轴是直线___________.图象的开口方向与函数y=ax2的图象_________. 向右(当m<0)或向左(当m>0)平移|m|个单位,(-m,0),x=-m,相同 2.二次函数y=a(x+m)2+k(a≠0)的图象及其特征 平移:一般地,函数y=a(x+m)2+k(a≠0)的图象,可以由函数y=ax2的图象___________________________________得到. 顶点:抛物线的顶点坐标为_____________. 对称轴:直线____________. 开口方向:抛物线y=a(x+m)2+k(a≠0)的开口与抛物线y=ax2的开口________,当a>0,开口向上,当a<0,开口向下. 最大(小)值:当a>0时抛物线有最低点,当x=-m时函数有最小值k;当a<0时,抛物线有最高点,当x=-m时函数有最大值k. 向右(当m<0)或向左(当m>0)平移|m|个单位,再向上(当k>0)或向下(当k<0)平移|k|个单位. (-m,k),x=-m,相同.
课题 1.2二次函数的图象(2) 单元 一 学科 数学 年级 九年级(上)
学习 目标 1.学会观察、归纳、概括函数图像的特征 2. 掌握y=ax2图象的位置关系及有关性质
重点 掌握二次函数y=a(x+m)2+k(a≠0)型的图象及其特征;
难点 二次函数的性质及二次函数的平移运用数形结合思想.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题 思考:二次函数y=ax 的图象及其特点? 二次函数y=a(x-m)2的图象与二次函数y=ax2的图象开口方向、对称轴和顶点坐标是否相同 那么 y=a(x-m)2+k的图象呢? 我们开始一起去研究! 试一试:在同一坐标系中作出下列二次函数: , 填表 描点画图 请比较所画三个函数的图象,它们有什么共同的特征 。 那么我们是否可以由我们学过的抛物线平移得到呢? 观察 由图知 向右平移 2 个单位得到. 顶点(0,0)向右平移2个单位得到 (2,0) 。 对称轴: 直线x=0向右平移2个单位得到直线 x=2 。 向左平移 2 个单位得到 顶点(0,0)向左平移2个单位得到 (-2,0) 。 对称轴: 直线x=0向左平移2个单位得到 x=-2 。 思考 自议 由抛物线y=ax2(a≠0)向左(m>0)平移|m|个单位,则得y=a(x+m)2(a≠0);由抛物线y=ax2(a≠0)向右(m<0)平移|m|个单位,则得y=a(x+m)2(a≠0). (1)已知抛物线的顶点坐标求解析式通常用y=a(x+m)2+k(a≠0)的形式,称为顶点式; (2)利用草图对求平移后的抛物线常常有所帮助.
讲授新课 提炼概念 总结:二次函数y=a(x- m)2的图象和性质. (
当
m<0
时
,
向左平移
)平移: (
当
m<0
时
,
向右平移
) y=a(x- m)2 a>0时,开口________, 最 ____ 点是顶点; a<0时,开口________, 最 ____ 点是顶点; 对称轴是 _____________, 顶点坐标是 __________。(向上,低;向下,高;直线x=m,(m,0) 三、典例精讲 例2 对于二次函数请回答下列问题 把函数的图象作怎样的平移变换,就能得到函数 的图象。 (2)说出函数的图象的顶点坐标和对称轴。 解:(1)函数的图象向右平移4个单位,就得到函数 的图象。 函数的图象的顶点坐标是(4,0),对称轴是直线x=4. 试一试: 用描点法在同一直角坐标系中画出下列函数的图象: 想一想 函数由函数的图象怎样平移得到的? 函数由函数的图象怎样平移得到的? 归纳性质: 一般地函数y=a(x+m)2+k的图象,函数y=ax2的图象只是位置不同, (1)可以由y=ax2的图象先向右(当m<0)或向左(当m>0)平移∣m∣个单位,再向上(当k>0)或向下(当k<0)平移∣k∣个单位得到, (2)顶点坐标是(-m,k),对称轴是直线x=-m, (3)图象在x轴的上方还是下方,开口方向向上还是向下等性质由y=ax2来决定的。 已知抛物线的顶点坐标,常设抛物线的顶点式y=a(x+m)2+k(a≠0). 解此类题可以将不同形式的解析式统一为y=a(x+m)2+k的形式,便于解答.
课堂检测 四、巩固训练 1.将抛物线y=2x2向上平移3个单位,再向右平移2个单位,所得到的抛物线为( ) A.y=2(x+2)2+3 B.y=2(x-2)2+3 C.y=2(x-2)2-3 D.y=2(x+2)2-3 B 填写下表: 解: 向下y轴(0,0)向上y轴(0,5)向下直线x=-4(-4,0)向上直线x=-2(-2,-7)
3.(1)将如图所示的图象向左平移2个单位,写出平移后的抛物线表达式; (2)将如图所示的图象向右平移3个单位,写出平移后抛物线的表达式. 解:向左平移2个单位的图象如图中y1;向右平移3个单位的图象,如图中y2. ∵原抛物线顶点为点(0,0)且过点(3,2), ∴设其表达式为y=ax2(a≠0), 且2=a×32. ∴a=,∴y=x2. (1)向左平移2个单位后:y=(x+2)2; (2)向右平移3个单位后:y=(x-3)2. 4.已知函数y=(x+1)2-4. (1)指出函数图象的开口方向、对称轴和顶点坐标; (2)若将该抛物线先向右平移2个单位,再向上平移4个单位,求得到的抛物线的解析式; (3)原抛物线经过怎样的平移后顶点在原点? 解:(1)顶点(-1,-4),开口向上,对称轴为直线x=-1; (2)y=(x-1)2; (3)y=(x+1)2-4向右平移1个单位,再向上平移4个单位.
课堂小结 1.二次函数y=a(x+m)2(a≠0)型的图象及其特征 平移:(1)一般地,函数y=a(x+m)2(a≠0)的图象与函数y=ax2的图象只是位置不同,它可由y=ax 的图象________________________________得到. 特征:函数y=a(x+m)2的图象的顶点坐标是_______,对称轴是直线___________.图象的开口方向与函数y=ax2的图象_________. 向右(当m<0)或向左(当m>0)平移|m|个单位,(-m,0),x=-m,相同 2.二次函数y=a(x+m)2+k(a≠0)的图象及其特征 平移:一般地,函数y=a(x+m)2+k(a≠0)的图象,可以由函数y=ax2的图象___________________________________得到. 顶点:抛物线的顶点坐标为_____________. 对称轴:直线____________. 开口方向:抛物线y=a(x+m)2+k(a≠0)的开口与抛物线y=ax2的开口________,当a>0,开口向上,当a<0,开口向下. 最大(小)值:当a>0时抛物线有最低点,当x=-m时函数有最小值k;当a<0时,抛物线有最高点,当x=-m时函数有最大值k. 向右(当m<0)或向左(当m>0)平移|m|个单位,再向上(当k>0)或向下(当k<0)平移|k|个单位. (-m,k),x=-m,相同.
同课章节目录
