2.6探索勾股定理2说课

课件33张PPT。《2.6探索勾股定理(二)》说课教师：安吉外国语学校 应飞教 材：九年制义务教育课程标准实验教科书
（浙教版）八年级上册 教材的地位及作用教学目标教学重点、难点教学方法与教学手段教学过程目录学情分析教材的地位及作用
(浙教版）八年级上册
第二章第六节 “探索勾股定理”
第二课时

学情分析第一：学生已经学习了勾股定理,对数形结合有了一定的认知 . 第二：八年级学生已经有一定的探索能力和解决问题的能力. 第三：我校是县直属的初级中学,学生天真活泼,对于新生事物 有浓厚兴趣,求知欲望强，学习热情高知识技能目标教学目标 发现观察交流体验说理归纳教学目标 过程与方法目标情感、态度、与价值观教学目标 教学重点:
由三角形三边关系判定
是否是直角三角形的方法 教学难点：
例2以及如何将三角形边的
数量关系经过代数变化，
最后达到一个目标式，
来判定是否是直角三角形。 教学设想教具、学具准备： 教具：多媒体课件
(2) 学具：自制学生学具
（长度为8cm、15cm、17cm统一规格小竹棒三根）
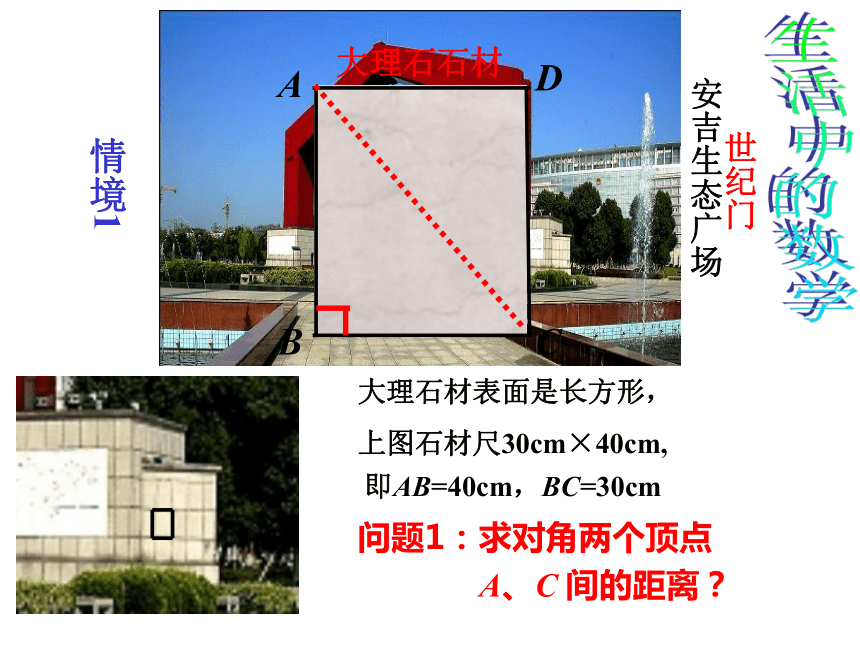
1、创设情境、导入新课教学程序情境1大理石材表面是长方形，
上图石材尺30cm×40cm,生活中的数学情境2生活中的数学情境3生活中的数学古埃及人曾用下面的方法得到直角：一个工匠同时握住绳子的第1个结和第13个结，两个助手分别握住第4个结和第8个结，拉紧绳子，就会得到一个直角三角形，其直角在第4个结处.三边满足32+42=52问题3:这样真能得到
直角三角形吗?2、活动与探究教学程序三个探究活动活动三：算一算 准备工作：
1、分别测量出三根小竹棒的长度，并作记录
2、每个三角形的三边长从小到大排列为a，b，c得到三组数,并填表格：3、知识应用,归纳猜想教学程序判定下列三角形是不是直角三角形？如果是,请指处哪条边所对的角是直角.(1) a=8， b=10 ， c=6 　　　　　　　　　　　(2) a=５， b=６， c= 2 1、先确定最长边；4、例题解析,当堂练习教学程序例1：根据下列条件,分别判断以a、b、c为边的三角形是不是直角三角形.⑴ a= ，b= 1 ，c=⑵ a=3n, b=4n, c=5n ( n为正整数)1、当三角形的三边是代数式形式时,为确定最大边可考虑直接比较或用取特殊值法比较边的大小 .2、降低例2的难度。 1、如何确定最长边?2、判定它是直角三角形，需要得到怎样的目标式？4、这样的目标式，能判断出哪个角是直角？3、目标式可能为？5、课堂小结教学程序课堂回眸3、如果两边的平方和等于第三边的平方， 那么这个三角形是直角三角形6、联系生活,解决问题教学程序情境2生活中的数学世纪门旁边有一块地，
已知，AD=4m，CD=3m，∠ADC=90°
AB=13m，BC=12m。求这块地的面积。补生活中的数学问题2：还可以解决哪些实际问题?7、布置作业
教学程序板 书 设 计2.6 探索勾股定理（二）

直角三角形 例 题1 例 题2
的判定方法
附：………………学生练习板演区设计意图一、源自生活，激情飞扬
兴趣是最好的老师，兴趣是学习的最大源动力。为了使学生长时间地保持旺盛的求知欲，本节课搭建了以学生所熟悉的生活情境为问题媒介，以一系列学生力所能及的的探究活动为依托，以经历探索特殊三角形三边之间的“数”的关系发现三角形有一个直角“形”的特点过程为主线，将数学知识串起来。这些贴近学生生活又具可操作性的问题、例题，就像给枯燥的数学披上夺目的外衣，更加激发学生的学习积极性和主动探究数学问题的激情。设计意图二、合理选材，优化教学
在教学中，忠实于教材，在研究的基础上创新了例题。随处可见学生思维碰撞的火花，发展了学生的思维能力，培养了学生思考的习惯，增强了学生运用数学知识解决实际问题的能力。设计意图三、自主探究，合作交流
整节课的设计以落实双基为起点，培养学生自主、合作、创造性学习的能力，重视知识的产生过程，关注人的发展。无论是教学环节设计，还是课外作业的安排上，我都注意到个体间的差异，注意分层教学，关注到个人的发展，让每一个学生在课堂都有所感悟，不同的人在数学上都得到不同的发展。感 谢
各位专家和老师email:yingfeidoudou@163.com