探索勾股定理2

课件29张PPT。2.6.2探索勾股定理湖州新世纪外国语学校　沈晖教材分析教学过程设计说明说课流程一、教学分析⒈地位与作用　　　探索勾股定理2，是在学习“勾股定理”内容之后的一个环节，即通过三角形的三边关系来判定直角三角形，它是初中阶段学习的重要内容之一，是判断直角三角形的重要方法，是前面知识的继续和深化。对以后无论是教学内容还是解题思维，将起十分广泛的作用。2.教学目标 ⒈知识目标：使学生了解勾股定理的逆定理并能应用它判断一个三角形是否为直角三角形。 ⒉能力目标：通过勾股定理与其逆定理的比较，提高学生的辨析能力；提高综合运用知识的能力。 ⒊情感目标：通过引例培养学生的爱国主义思想；通过自主学习来体验获取数学知识的感受。 3.教学重点与难点 ⑴教学重点：勾股定理逆定理的应用 ⑵教学难点：探索出勾股定理的逆定理 3.教法和学法 作图发现法，探究验证法，交流讨论法　　通过探索新知，巩固运用，合作交流，以及例题和习题的设计，都是为了加强学生的说理和推理能力。二、教学过程 （一）复习回顾，提出问题 （二）合作学习，探索新知 （三）归纳结论，例题示范 （四）拓展提高，体验成功 （五）归纳小结，反思提高 （六）布置作业
1.直角三角形的两边长分别是3cm、4cm，则第三边长是_____________
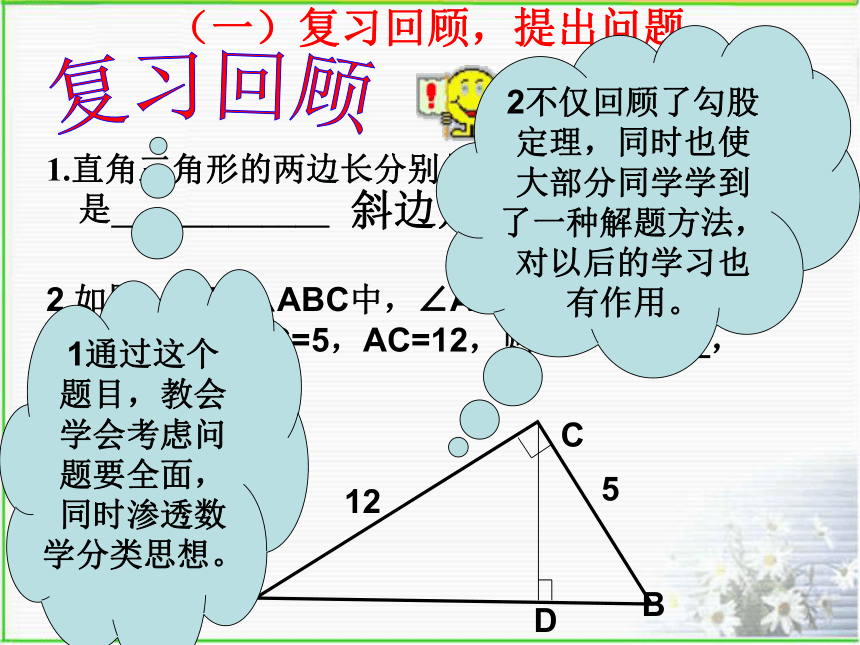
复习回顾512132.如图，在Rt△ABC中，∠ACB＝Rt∠，CD⊥AB，若BC=5，AC=12，则AB＝_____，
CD＝＿＿＿＿
（一）复习回顾，提出问题 斜边是＿＿＿＿＿1通过这个题目，教会学会考虑问题要全面，同时渗透数学分类思想。2不仅回顾了勾股定理，同时也使大部分同学学到了一种解题方法，对以后的学习也有作用。　　王伟是我们湖州人的骄傲。在湖州的凤凰公园有一座王伟的塑像。
星期天，小明在凤凰公园里游玩。爱动脑筋的小明想要检测塑像底座正面的 AD 边是否垂直于底边AB,但他随身只带了卷尺。 你想知道小明是如何解决这个问题吗?想一想这个引入学生也感觉亲切，对引入的处理，我觉得如果让他们直接回答，可能很费时间，二来也可能说不清，容易混淆勾股定理。为充分利用时间，照顾到全体的学生的学习。直接进入新课的学习。二、教学过程 （一）复习回顾，提出问题 （二）合作学习，探索新知 （三）归纳结论，例题示范 （四）拓展提高，体验成功 （五）归纳小结，反思提高 （六）布置作业 画一画：画一个三角形,使其三边长为:3cm, 4cm, 5cm　　用量角器量一量最大的角，判断它们是什么三角形？量一量：（二）合作学习，探索新知尺规作图，学生有些遗忘，老师在黑板上画，和学生一起回顾。然后学生模仿上面的画法。这样做不让学生盲目地来画图，而在回顾尺规作图的基础上进行规范操作。这样既能准确地运用知识，而且也不浪费时间。效果比较好。 算一算：猜一猜：　　如果一个三角形有两边平方和等于第三边的平方，那么这个三角形一定是直角三角形 。 a2+b2=c2提问方式。区分勾股定理与逆定理，初步明确互逆的意义。二、教学过程 （一）复习回顾，提出问题 （二）合作学习，探索新知 （三）归纳结论，例题示范 （四）拓展提高，体验成功 （五）归纳小结，反思提高 （六）布置作业 　　如果一个三角形有两边平方和等于第三边的平方，那么这个三角形一定是直角三角形 。　　如果三角形中两条较短边的平方和等于最长边的平方，那么这个三角形是直角三角形，并且最长边所对的角是直角。 以6，8，10为三边的三角形是直角三角形吗？∴以6，8，10为边的三角形是直角三角形 结论归纳得到换一种形式的必要性（三）归纳结论，例题示范例1 根据下列条件，分别判断以a,b,c为边的三角形是不是直角三角形
(1) a＝9，b＝12，c＝15
(2) a＝ , b＝1，c＝解:(1)∵92+122＝152，∴以9,12,15为边三角形是直角三角形判断1、根据下列条件，判断下面以a、b、c 为边的三角形是不是直角三角形
(1) 　a=5，b=7，c=8
(2)
c2=b2-a2
a:b:c=3:4:5看谁做得快ABCD 现在你知道小明是如何用一把卷尺来说明雕塑底座正面的AD 边是否垂直于底边AB的吗？ 小明量得AD长是4米，AB长是3米，BD长是5米，AD边垂直于AB边吗？你现在知道他是怎么做的吗？34学以致用例2、已知△ABC三条边长分别为a,b,c，且a＝m2－n2，b＝2mn，c＝m2＋n2(m>n，m,n是正整数)。△ABC是直角三角形吗？请说明理由.解：∵ a=m2－n2，b=2mn，c＝m2＋n2∴a2+b2=(m2－n2)2+(2mn)2＝m4－2m2n2＋n4＋4m2n2＝(m2＋n2)2＝m4＋2m2n2＋n4＝c2∴△ABC是直角三角形二、教学过程 （一）复习回顾，提出问题 （二）合作学习，探索新知 （三）归纳结论，例题示范 （四）拓展提高，体验成功 （五）归纳小结，反思提高 （六）布置作业 1.如图，在ΔABC中，D是BC上的一点，AB＝20，BD＝16，DC＝9，AD＝12。请找出图中的有 个直角三角形。 拓展与应用2016912153（四）、拓展提高，体验成功拓展与应用2.如图，已知一个四边形的四条边AB，BC，CD和DA的长分别是3，4，13和12，其中∠B=90°，求这个四边形的面积。能正确区分勾股定理及逆定理的区别与联系，条件与结论。并能灵活运用。一个题目中出现了这两个知识点，对比着运用有助于掌握。例2的变式，通过沿AC对折，学生很容易回答。 二、教学过程 （一）复习回顾，提出问题 （二）合作学习，探索新知 （三）归纳结论，例题示范 （四）拓展提高，体验成功 （五）归纳小结，反思提高 （六）布置作业 感悟与反思（五）、归纳小结，反思提高归纳小结勾股定理
直角三角形两直角边的平方和等于斜边的平方．　　如果三角形两较短边的边平方和等于最长边平方, 那么这个三角形是直角三角形.直角三角形的判定方法：互逆六、布置作业必做题：作业本、书本42页作业题
选做题1：
边长满足关系(a-b)(a2+b2-c2)=0的△ABC是什么三角形？
A、直角三角形
B、等腰三角形
C、等腰直角三角形
D、直角三角形或等腰三角形
请在下面正方形方格上作格点直角三角形，且顶点必须在格点上。你能找出多少种不全等的直角三角形，并和你的同学交流。
选做题2板书设计 投影区板演区作图区课题三、设计说明一、引入部分的处理：引入的这个例子，说明数学从生活中来又到生活中去。两个方面：
1从身边的例子出发，激发学生的学习兴趣；
2因为王伟是湖州人的骄傲，通过这个例子，也对学生进行爱祖国，爱家乡的情感渗透。
二、探索新知的过程：采用画一画，量一量，算一算，猜一猜等，主要是为了让学生自己亲身经历知识的形成过程，体验成功的喜悦。而不是简单的教师讲，学生听的旧模式。当然这里的提问形式的引导等我觉得非常重要，目的是引导学生得到逆定理的条件和结论，不至于和勾股定理混淆。
三、知识的应用方面：我觉得有两个难点
1．两边的平方和的处理，通过例子让学生回答两边，第三边分别是什么边，并及时总结；通过类比三角形两边之和大于第三边，进一步加深学生的印象，并强调。这个效果比较好。
2．弄清勾股定理与逆定理的关系，这是容易混淆的。通过投影学生书写的过程，回答等形式。暴露学生的思维过程，及时订正，加深印象。 感谢各位