2.1直线与圆的位置关系课件

课件20张PPT。已知⊙O的半径为5（1）若PO=5.5，则点P在 ；（2）若PO=4，则点P在 ；（3）若PO= ，则点P在圆上。圆外圆内5一：复习回顾 一般地，如果用r表示圆的半径，d表示同一平面内点到圆心的距离，则有：2.1 直线与圆的位置关系
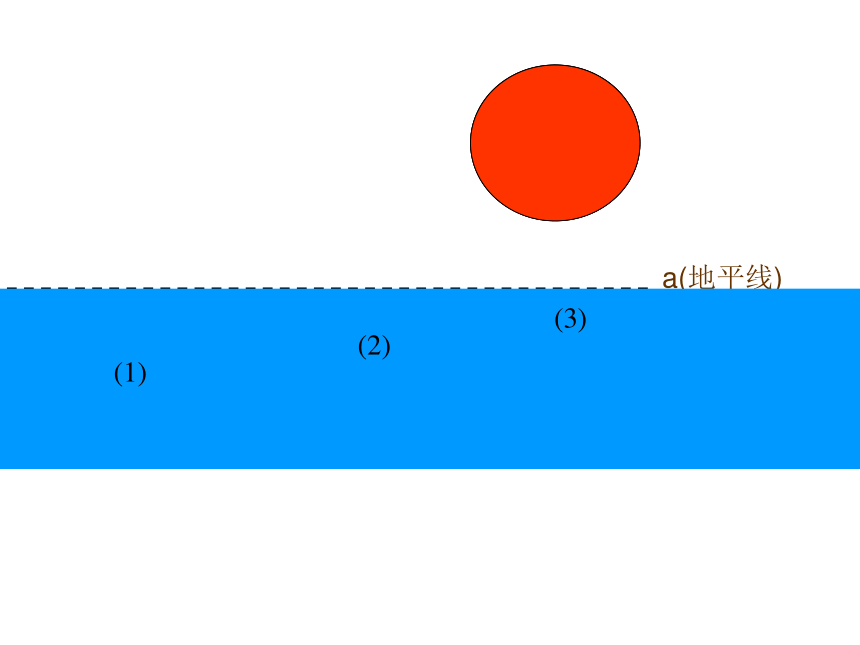
（1）如果我们把太阳看成一个圆，地平线看成一条直线,那你能根据直线与圆的公共点的个数进行归纳分类呢？a(地平线)
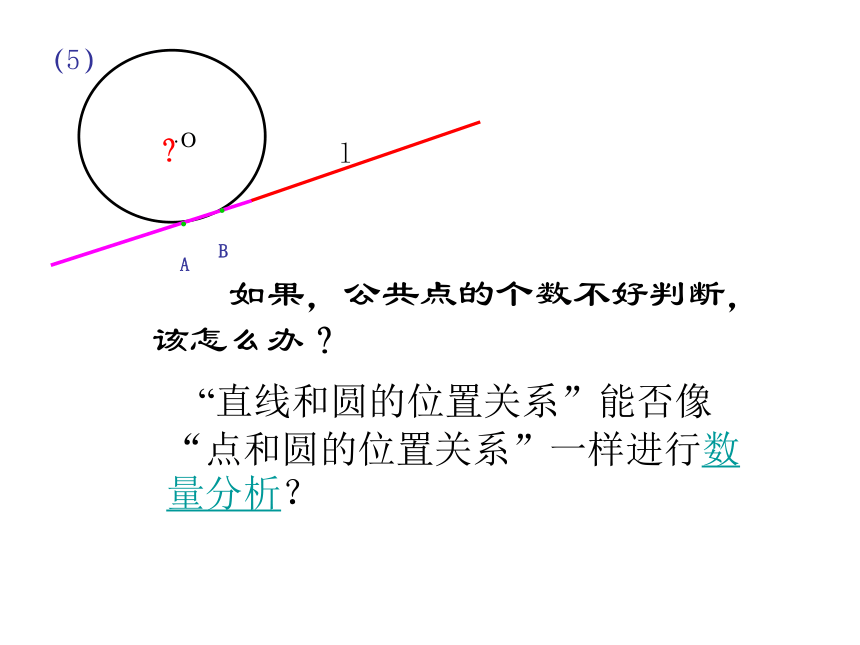
(1)(3)(2)(1)直线和圆没有公共点(2)直线和圆有唯一公共点 (3)直线和圆有两个公共点 直线和圆的位置有下列三种情况: 叫做直线和圆相离 叫做直线和圆相切,这条直线叫圆的切线，这个公共点叫切点叫做直线和圆相交.（根据直线 与圆的公共点的个数来分） 看图判断直线l与 ⊙O的位置关系（1）（2）（3）（4）相离相切相交相交？llll·O·O·O·O（5）l·O（5）？l 如果，公共点的个数不好判断，该怎么办？·O·
A·
B “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析？如图.O为直线l外一点，OT⊥l，且OT=d.请以O为圆心，分别以 r＜d, r=d, r＞d 为半径画圆.所画的圆与直线l有什么位置关系?做一做2、d = r直线和圆相切3、d < r
直线和圆相交dr二、直线和圆的位置关系（用圆心O到直线l的距离d与圆的半径r的关系来区分）1、d > r
直线和圆相离判定直线与圆的位置关系的方法有____种：（1）由________________ 的个数来判断；（2）由___________________________ 的
数量大小关系来判断．两直线与圆的公共点圆心到直线的距离d与半径r
在实际应用中，常采用第二种方法判定。2、d = r直线和圆相切3、d < r
直线和圆相交dr二、直线和圆的位置关系（用圆心O到直线l的距离d与圆的半径r的关系来区分）1、d > r
直线和圆相离二、直线与圆的位置关系的性质和判定
巩固： 1 、 设⊙O的半径为r,圆心O到直线L的距离为d,
根据下列条件判断直线L与⊙O的位置关系:
（1）d=4,r=3∵d＞ r∴直线l与⊙O相离∵d＝r∴直线l与⊙O相切2、⊙O的半径为r ,圆心O到直线l的距离为3,若直线l与⊙O相交，则r为（　）：
　A．r＞3 B．0＜r<3 C．0＜r ≤3 D．r =3A 3、在△ABC 中，∠ACB=90°，AC=3cm，BC=4cm，
设⊙C的半径为r,若⊙C与直线AB相离时，则r
的取值是_______________．
ABC3cm4cm2.4cmr＜2.40⊙P与BC相切.求证： ⊙P与AB相切DE证明：过P作PD⊥AB，PE⊥BC分别交AB、BC于点D、E
设⊙P的半径为r

∵点P在∠ABC的角平分线上
∴PD=PE又∵ ⊙P与BC相切

∴PE=r
∴PD=r∴⊙P与AB相切
船有无触礁的危险 例2：在码头Ａ的北偏东６０°方向有一个海岛，离该岛中心Ｐ点１２海里的范围内是一个暗礁区。货船从码头Ａ由西向东方向航行，行驶了１０海里到达Ｂ点，这时岛中心Ｐ在北偏东４５°方向。
若货船不改变航向，你认为货船会有触礁的危险吗?PABH600450暗礁区例. 在码头A的北偏东60°方向有一个海岛，离该岛中心P的12海里范围内是一个暗礁区。货船从码头A由西向东方向航行，行驶了10海里到达B，这时岛中心P在北偏东45°方向。若货船不改变航向，问货船会不会进入暗礁区？解:如图,作PH⊥AB,垂足为H.则∠PAH=30°∠PBH=45°，∴货船不会进入暗礁区∵AH-BH=AB=10∵13.66＞12PABH600450巩固提升如图，直线AB，CD相交于点O，∠AOC=30o,半径为1cm的⊙P
的圆心在直线AB上，开始时，PO=6cm,如果⊙P以1cm/s的速度
由点A向点B的方向移动，那么当⊙P的运动时间t(s)满足什么条件
时， ⊙P与直线CD相交直线与圆的位置关系dr 2交点1切点0归纳与小结无再见！谢谢指导再见