2.2切线长定理课件
图片预览

文档简介
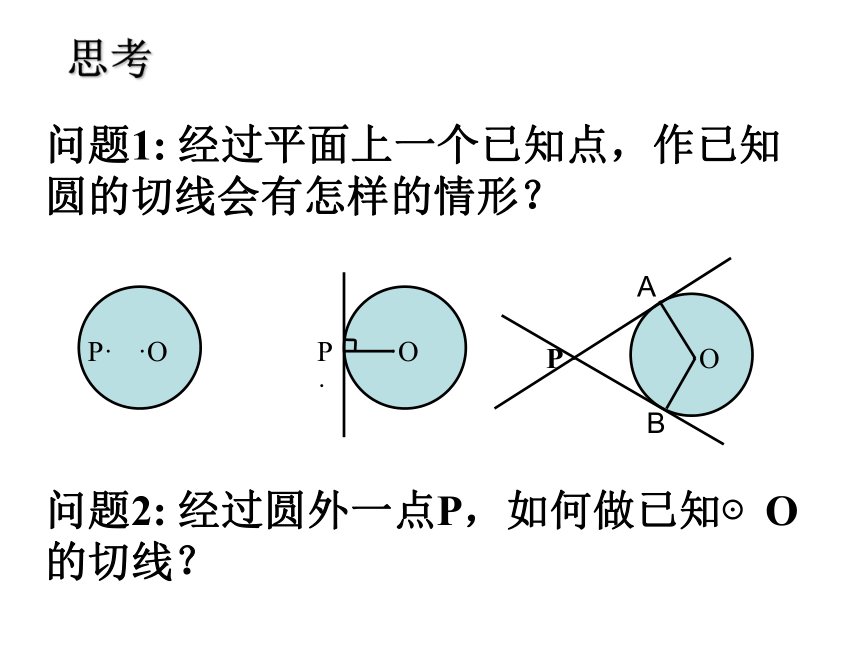
课件19张PPT。2.2切线长定理问题1: 经过平面上一个已知点,作已知圆的切线会有怎样的情形?P ·P·P ·问题2: 经过圆外一点P,如何做已知⊙O的切线?AB思考50° 如何过⊙O外一点P画出⊙O的切线?
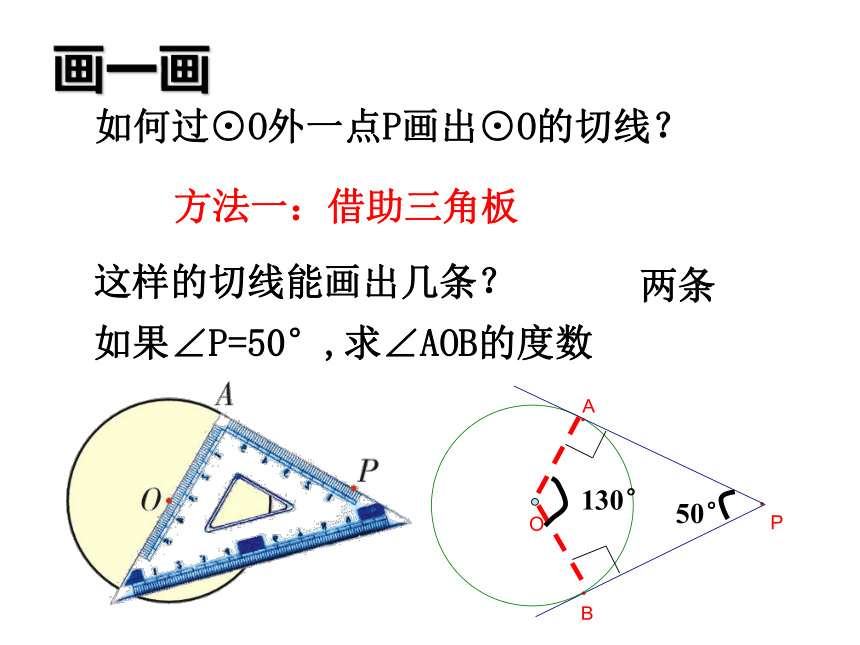
这样的切线能画出几条?如果∠P=50°,求∠AOB的度数130°画一画两条方法一:借助三角板 OABP如何用圆规和直尺作出这两条切线呢?.思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°,
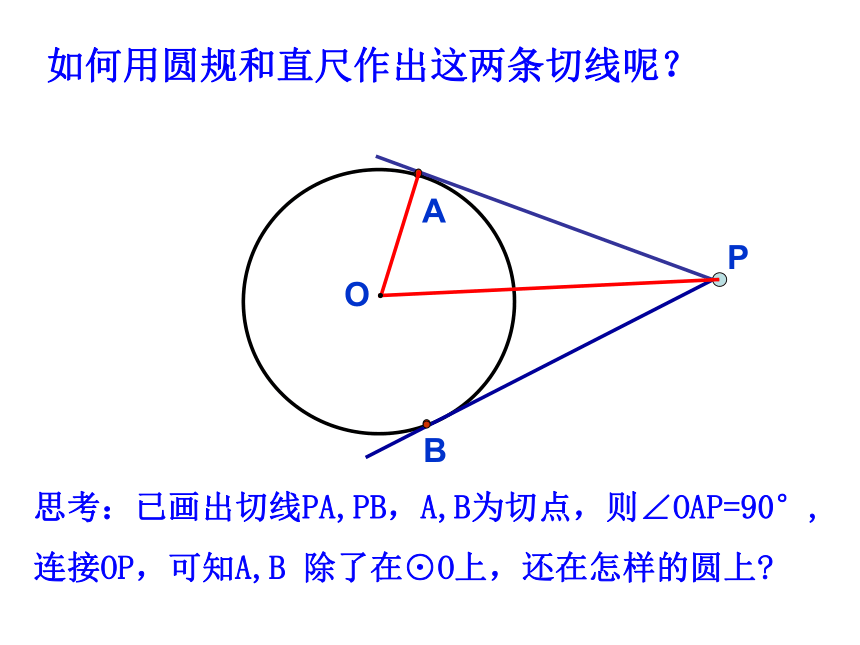
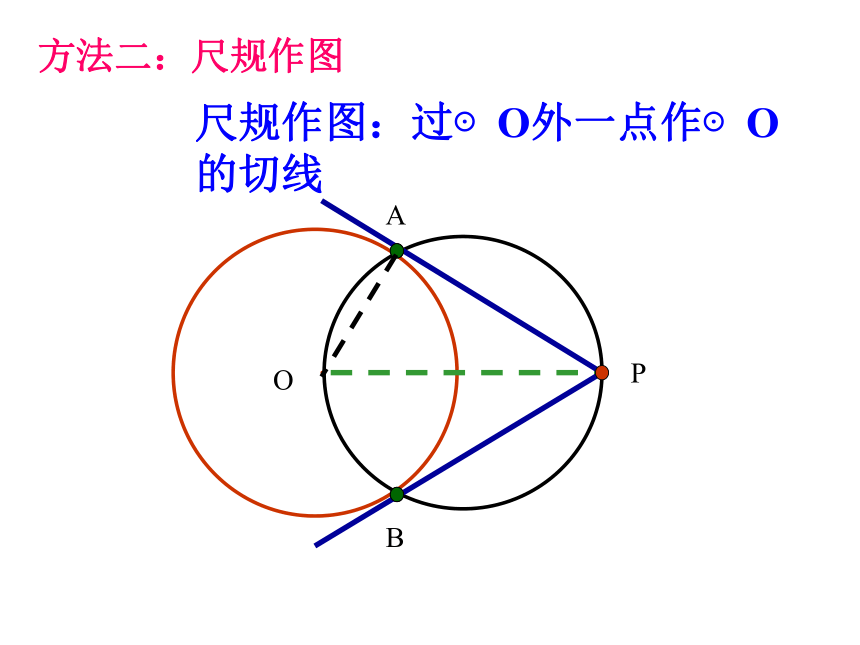
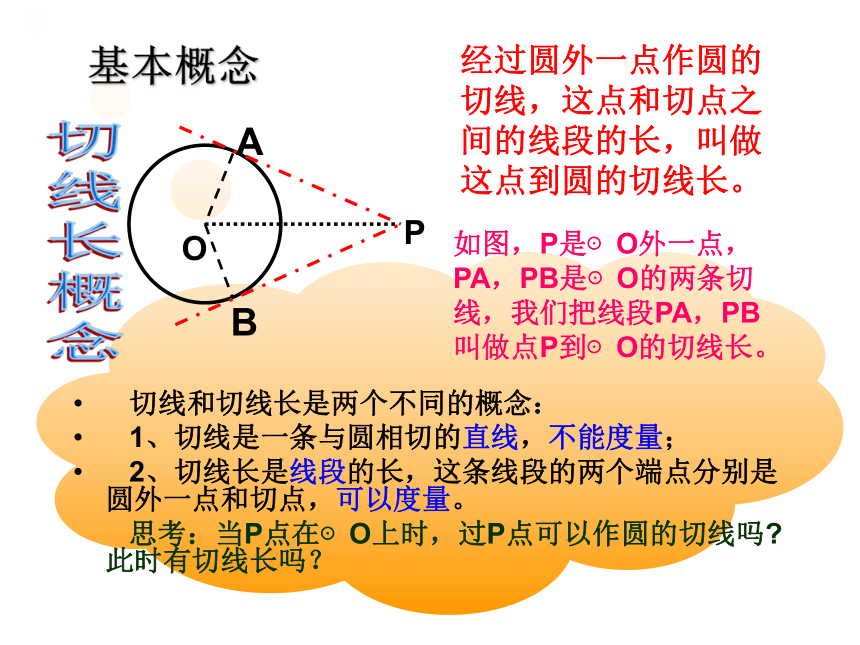
连接OP,可知A,B 除了在⊙O上,还在怎样的圆上?尺规作图:过⊙O外一点作⊙O的切线O ·PABO方法二:尺规作图切线长概念如图,P是⊙O外一点,PA,PB是⊙O的两条切线,我们把线段PA,PB叫做点P到⊙O的切线长。经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长。 切线和切线长是两个不同的概念:
1、切线是一条与圆相切的直线,不能度量;
2、切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。
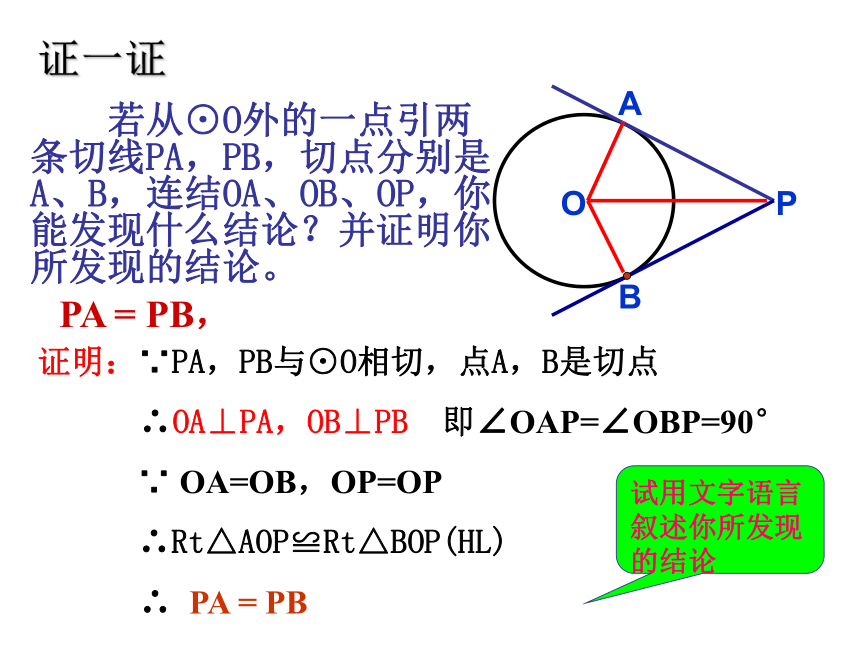
思考:当P点在⊙O上时,过P点可以作圆的切线吗?此时有切线长吗?基本概念 若从⊙O外的一点引两条切线PA,PB,切点分别是A、B,连结OA、OB、OP,你能发现什么结论?并证明你所发现的结论。PA = PB,试用文字语言叙述你所发现的结论
P证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB证一证PA、PB与⊙O分别相切于点A、BPA = PB几何语言:从圆外一点引圆的两条切线,它们的切线长相等,切线长定理 若从⊙O外的一点引两条切线PA,PB,切点分别是A、B,连结OA、OB、OP,你还能发现什么结论?∠OPA=∠OPBP证明:∵PA,PB与⊙O相切,点A,B是切点
∴PA=PB
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(SSS)
∠OPA=∠OPB证一证APOB1.若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB牛刀小试BPO。A2.若延长PO交⊙O于点C,连结AC、BC,你又能得出什么新的结论?并给出证明.AC=BC,证明:连结OA、OB
∵PA,PB与⊙O相切,点A,B是切点
PA=PB
∴△AOP≌△BOP(SSS)
∴ ∠OPA=∠OPB
又∵ PA = PB, PC=PC
∴△PCA ≌ △PCB
∴AC=BC,∠OCA=∠OCBC∠OCA=∠OCB见作业题4牛刀再试 若PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
BAPOCED(3)写出图中所有的垂直关系OA⊥PA,OB ⊥PB,AB ⊥OP(5)写出图中所有的全等三角形△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP(4)写出图中所有的等腰三角形△ABP △AOB(1)写出图中所有相等的线段AO=BO=DO=EO,AP=BP,AC=BC(2)写出图中所有相等的弧AD=BD,AE=BE,DAE=DBE定理拓展。PBAO(3)连结圆心和圆外一点(2)连结两切点(1)分别连结圆心和切点反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形,添加辅助线。归纳反思一、判断:
过任意一点总可以作圆的两条切线( )二、选 择:
如图所示,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )AABPDEOC练 习已知:在⊙O中,AC、BC分别为⊙O的切线,A、B为切点,已知∠ACB=800,OC=100cm,求C到⊙O的切线长。(结果精确到1cm)CBOA例题1如图:⊙O表示皮带转动装置的一个轮子,传动皮带MA、NB分别为⊙O的切线,A、B为切点,延长MA、NB相交于点P,已知∠APB=600,AP=24cm,求两切点间的距离和弧AB的长(结果精确到1cm)MNMNMN例题21、已知⊙O的半径为5,P是⊙O外一点,PO=10,求点P到⊙O的切线长和两切点间的劣弧长。 OABMN2、已知:在⊙O中,弦AB垂直平分半径ON,过点A、B的切线相交于点M,求证△ABM为等边三角形。课内练习1、已知:在⊙O中,PA、PB分别为⊙O的切线,A、B为切点,已知⊙O的半径为1 ,OP=2.4,求切线长。(精确到0.1)和∠APB的度数。PBOA作业题完成作业题2、3、51.切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 ∵PA、PB分别切⊙O于A、B∴PA = PB ,∠OPA=∠OPB切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。BAP课堂小结
这样的切线能画出几条?如果∠P=50°,求∠AOB的度数130°画一画两条方法一:借助三角板 OABP如何用圆规和直尺作出这两条切线呢?.思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°,
连接OP,可知A,B 除了在⊙O上,还在怎样的圆上?尺规作图:过⊙O外一点作⊙O的切线O ·PABO方法二:尺规作图切线长概念如图,P是⊙O外一点,PA,PB是⊙O的两条切线,我们把线段PA,PB叫做点P到⊙O的切线长。经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长。 切线和切线长是两个不同的概念:
1、切线是一条与圆相切的直线,不能度量;
2、切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。
思考:当P点在⊙O上时,过P点可以作圆的切线吗?此时有切线长吗?基本概念 若从⊙O外的一点引两条切线PA,PB,切点分别是A、B,连结OA、OB、OP,你能发现什么结论?并证明你所发现的结论。PA = PB,试用文字语言叙述你所发现的结论
P证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB证一证PA、PB与⊙O分别相切于点A、BPA = PB几何语言:从圆外一点引圆的两条切线,它们的切线长相等,切线长定理 若从⊙O外的一点引两条切线PA,PB,切点分别是A、B,连结OA、OB、OP,你还能发现什么结论?∠OPA=∠OPBP证明:∵PA,PB与⊙O相切,点A,B是切点
∴PA=PB
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(SSS)
∠OPA=∠OPB证一证APOB1.若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB牛刀小试BPO。A2.若延长PO交⊙O于点C,连结AC、BC,你又能得出什么新的结论?并给出证明.AC=BC,证明:连结OA、OB
∵PA,PB与⊙O相切,点A,B是切点
PA=PB
∴△AOP≌△BOP(SSS)
∴ ∠OPA=∠OPB
又∵ PA = PB, PC=PC
∴△PCA ≌ △PCB
∴AC=BC,∠OCA=∠OCBC∠OCA=∠OCB见作业题4牛刀再试 若PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
BAPOCED(3)写出图中所有的垂直关系OA⊥PA,OB ⊥PB,AB ⊥OP(5)写出图中所有的全等三角形△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP(4)写出图中所有的等腰三角形△ABP △AOB(1)写出图中所有相等的线段AO=BO=DO=EO,AP=BP,AC=BC(2)写出图中所有相等的弧AD=BD,AE=BE,DAE=DBE定理拓展。PBAO(3)连结圆心和圆外一点(2)连结两切点(1)分别连结圆心和切点反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形,添加辅助线。归纳反思一、判断:
过任意一点总可以作圆的两条切线( )二、选 择:
如图所示,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )AABPDEOC练 习已知:在⊙O中,AC、BC分别为⊙O的切线,A、B为切点,已知∠ACB=800,OC=100cm,求C到⊙O的切线长。(结果精确到1cm)CBOA例题1如图:⊙O表示皮带转动装置的一个轮子,传动皮带MA、NB分别为⊙O的切线,A、B为切点,延长MA、NB相交于点P,已知∠APB=600,AP=24cm,求两切点间的距离和弧AB的长(结果精确到1cm)MNMNMN例题21、已知⊙O的半径为5,P是⊙O外一点,PO=10,求点P到⊙O的切线长和两切点间的劣弧长。 OABMN2、已知:在⊙O中,弦AB垂直平分半径ON,过点A、B的切线相交于点M,求证△ABM为等边三角形。课内练习1、已知:在⊙O中,PA、PB分别为⊙O的切线,A、B为切点,已知⊙O的半径为1 ,OP=2.4,求切线长。(精确到0.1)和∠APB的度数。PBOA作业题完成作业题2、3、51.切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 ∵PA、PB分别切⊙O于A、B∴PA = PB ,∠OPA=∠OPB切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。BAP课堂小结
