浙教版数学八年级上册 5.2函数2课件(共14张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 5.2函数2课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 20:55:03 | ||
图片预览






文档简介
(共15张PPT)
5.2 函数(2)
1.会列简单实际问题中的函数表达式;
2.会根据函数表达式,已知自变量的值,求相应的函数值,
或根据已知函数值求相应自变量的值;
3.会在简单情况下求求一些函数自变量的取值范围。
阅读书本P146—147例2,完成下列任务:
1.例1中有哪些变量,分别表示什么?如何求函数解析式?
先找函数与自变量之间的等式,然后求函数关于自变量的解析式。
2.自变量X的取值范围从哪几个方面考虑?
①代数式要有意义; ②符合实际。
3.结合例1、例2思考函数包含哪几类的基本问题?
如何解决?
当x取何值时,下列函数有意义。
1、y=
∵x-8≠0
∴x≠8
2、y=
∵2x- 4≥0
∴x ≥2
3、y=(3x+2)0
∵3x+2≠0
∴x≠
4、儿童节的时候,每人发2颗糖果,总人数x与总发的糖果数y的函数关系式为____________,其中人数x的取值范围是___________。
y= 2x
x为正整数
5、y=3x-6
x取一切实数
自变量的取值范围:
①代数式要有意义;
②符合实际
1、求下列函数自变量的取值范围(使函数式有意义):
2、求函数 自变量的取值范围.
(1)y=3x-1; (2) y=2x2+7;
(3) ; (4).
例1等腰三角形ABC的周长为10,底边BC长为y, 腰AB长为x,求:(1) y 关于x 的函数解析式;
(2)自变量的取值范围;
(3)腰长AB=3时,底边的长.
当 = 6时, =10 - 2 的值是多少 对本例有意义吗 当 = 2 呢
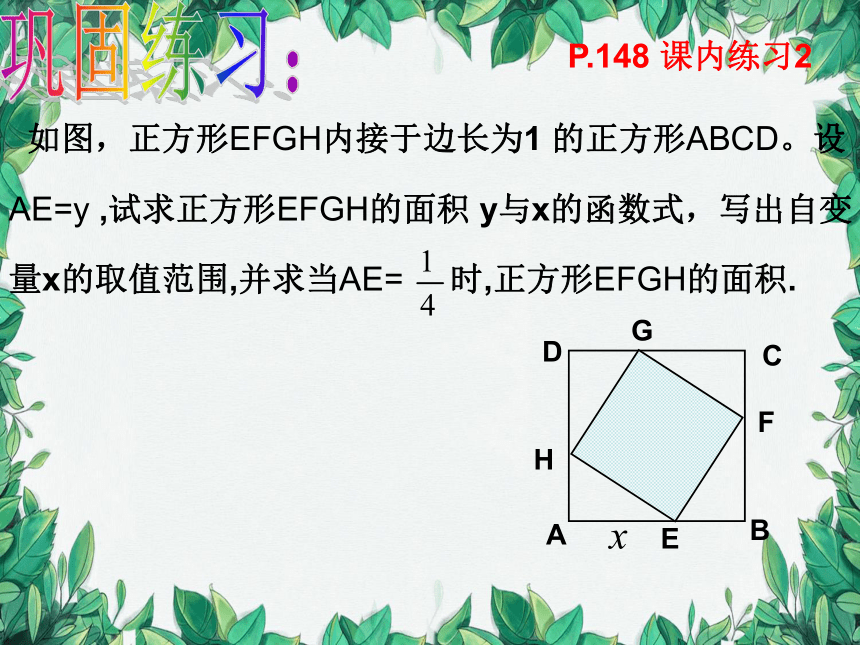
如图,正方形EFGH内接于边长为1 的正方形ABCD。设
AE=y ,试求正方形EFGH的面积 y与x的函数式,写出自变
量x的取值范围,并求当AE= 时,正方形EFGH的面积.
H
G
F
E
D
C
B
A
P.148 课内练习2
(2)放水 2 时20分后,游泳池内还剩水多少立方米
(3)放完游泳池内全部水需要多少时间
(1)求Q关于 t 的函数解析式和自变量 t 的取值范围;
例2 游泳池应定期换水. 某游泳池在一次换水前存水936立方米,换水时打开排水孔, 以每时312立方米的速度将水放出.设放水时间为 t 时,游泳池内的存水量为Q立方米.
三类函数的基本问题:
①求解析式
先得到函数与自变量之间的等式,然后求出函数关于自变量的函数解析式。
②求自变量的取值范围
①代数式要有意义 ②符合实际
③已知自变量的值求相应的函数值----当抄代算
已知函数值求相应的自变量的值----转化为方程
某市出租车起步价是10元(路程小于或等于3千米),超过3千米每增加1千米加收1.5元。
1.你能写出出租车车费y(元)与行程x(千米)之间的 函数关系式吗?
2.李老师乘车8千米,应付多少车费?
3.李老师若应付车费29元,那么他乘车多少千米?
P.148 作业题1、2、3、 4、5
已知一条钢筋长为100cm,把它折弯成长方形(或正方形),其中一条边长记为 x (cm),面积为 S (cm2)。求:
(1) S关于 x 的函数解析式;
(2)自变量 x 的取值范围。
(3)利用所写的解析式计算当 x =20,25,28时,S的值是多少?
x
(50-x)
S= x(50-x)
解:(1)
(3)当x=20时,S=20(50-20)
=20×30
=600 cm2
x>0
50-x>0
∵
∴ 0(2)
当x=55时, S= x(50-x)的值是多少
对本题有意义吗
P.148 作业题5
拓展提高:等腰直角△ABC的直角边长与正方形MNPQ的边长均为10 cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出△ABC运动过程中,重叠部分面积ycm2与MA长度x cm之间的函数关系式,并写出自变量x的取值范围.
如图,每个图形都是由若干个棋子围成的正方形图案的每条边(包括两个顶点)上都有 个棋子,设每个图案的棋子总数为 S.
图中棋子的排列有什么规律 S与 n 之间能用函数解析式表示吗 自变量n的取值范围是什么
合作探究
三类函数的基本问题:
①求解析式
先得到函数与自变量之间的等式,然后求出函数关于自变量的函数解析式。
②求自变量的取值范围
①代数式要有意义 ②符合实际
③已知自变量的值求相应的函数值----当抄代算
已知函数值求相应的自变量的值----转化为解方程
5.2 函数(2)
1.会列简单实际问题中的函数表达式;
2.会根据函数表达式,已知自变量的值,求相应的函数值,
或根据已知函数值求相应自变量的值;
3.会在简单情况下求求一些函数自变量的取值范围。
阅读书本P146—147例2,完成下列任务:
1.例1中有哪些变量,分别表示什么?如何求函数解析式?
先找函数与自变量之间的等式,然后求函数关于自变量的解析式。
2.自变量X的取值范围从哪几个方面考虑?
①代数式要有意义; ②符合实际。
3.结合例1、例2思考函数包含哪几类的基本问题?
如何解决?
当x取何值时,下列函数有意义。
1、y=
∵x-8≠0
∴x≠8
2、y=
∵2x- 4≥0
∴x ≥2
3、y=(3x+2)0
∵3x+2≠0
∴x≠
4、儿童节的时候,每人发2颗糖果,总人数x与总发的糖果数y的函数关系式为____________,其中人数x的取值范围是___________。
y= 2x
x为正整数
5、y=3x-6
x取一切实数
自变量的取值范围:
①代数式要有意义;
②符合实际
1、求下列函数自变量的取值范围(使函数式有意义):
2、求函数 自变量的取值范围.
(1)y=3x-1; (2) y=2x2+7;
(3) ; (4).
例1等腰三角形ABC的周长为10,底边BC长为y, 腰AB长为x,求:(1) y 关于x 的函数解析式;
(2)自变量的取值范围;
(3)腰长AB=3时,底边的长.
当 = 6时, =10 - 2 的值是多少 对本例有意义吗 当 = 2 呢
如图,正方形EFGH内接于边长为1 的正方形ABCD。设
AE=y ,试求正方形EFGH的面积 y与x的函数式,写出自变
量x的取值范围,并求当AE= 时,正方形EFGH的面积.
H
G
F
E
D
C
B
A
P.148 课内练习2
(2)放水 2 时20分后,游泳池内还剩水多少立方米
(3)放完游泳池内全部水需要多少时间
(1)求Q关于 t 的函数解析式和自变量 t 的取值范围;
例2 游泳池应定期换水. 某游泳池在一次换水前存水936立方米,换水时打开排水孔, 以每时312立方米的速度将水放出.设放水时间为 t 时,游泳池内的存水量为Q立方米.
三类函数的基本问题:
①求解析式
先得到函数与自变量之间的等式,然后求出函数关于自变量的函数解析式。
②求自变量的取值范围
①代数式要有意义 ②符合实际
③已知自变量的值求相应的函数值----当抄代算
已知函数值求相应的自变量的值----转化为方程
某市出租车起步价是10元(路程小于或等于3千米),超过3千米每增加1千米加收1.5元。
1.你能写出出租车车费y(元)与行程x(千米)之间的 函数关系式吗?
2.李老师乘车8千米,应付多少车费?
3.李老师若应付车费29元,那么他乘车多少千米?
P.148 作业题1、2、3、 4、5
已知一条钢筋长为100cm,把它折弯成长方形(或正方形),其中一条边长记为 x (cm),面积为 S (cm2)。求:
(1) S关于 x 的函数解析式;
(2)自变量 x 的取值范围。
(3)利用所写的解析式计算当 x =20,25,28时,S的值是多少?
x
(50-x)
S= x(50-x)
解:(1)
(3)当x=20时,S=20(50-20)
=20×30
=600 cm2
x>0
50-x>0
∵
∴ 0
当x=55时, S= x(50-x)的值是多少
对本题有意义吗
P.148 作业题5
拓展提高:等腰直角△ABC的直角边长与正方形MNPQ的边长均为10 cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出△ABC运动过程中,重叠部分面积ycm2与MA长度x cm之间的函数关系式,并写出自变量x的取值范围.
如图,每个图形都是由若干个棋子围成的正方形图案的每条边(包括两个顶点)上都有 个棋子,设每个图案的棋子总数为 S.
图中棋子的排列有什么规律 S与 n 之间能用函数解析式表示吗 自变量n的取值范围是什么
合作探究
三类函数的基本问题:
①求解析式
先得到函数与自变量之间的等式,然后求出函数关于自变量的函数解析式。
②求自变量的取值范围
①代数式要有意义 ②符合实际
③已知自变量的值求相应的函数值----当抄代算
已知函数值求相应的自变量的值----转化为解方程
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
