八上第一章三角形的初步知识专题-专题04 全等三角形基本模型(4大模型)(含解析)
文档属性
| 名称 | 八上第一章三角形的初步知识专题-专题04 全等三角形基本模型(4大模型)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 11:23:46 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专题04 全等三角形基本模型(4大模型)
重难点题型归纳
【模型一:平移型】
【模型二:翻折型】
【模型三:旋转型】
【模型四:一线三垂直型】
【模型一:平移型】
【典例1】如图,已知点E、C在线段BF上, , , .求证: .
【变式1-1】如图,已知Rt△ABC与Rt△DEF中,∠A=∠D=90°,点B、F、C、E在同一直线上,且AB=DE,BF=CE,求证:∠B=∠E.
【变式1-2】已知:如图,点F、C在线段BE上,AB=DE,∠B=∠E,BF=EC.求证:∠A=∠D.
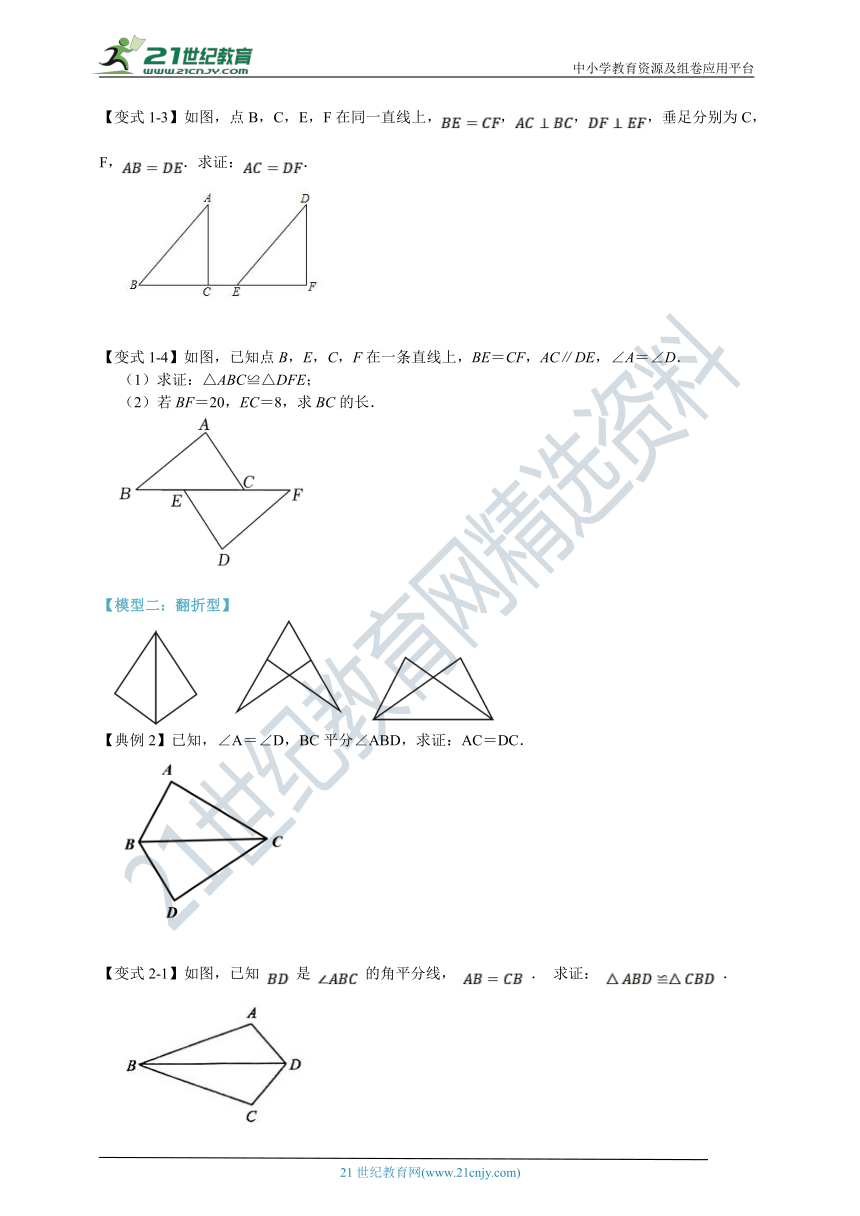
【变式1-3】如图,点B,C,E,F在同一直线上,,,,垂足分别为C,F,.求证:.
【变式1-4】如图,已知点B,E,C,F在一条直线上,BE=CF,AC∥DE,∠A=∠D.
(1)求证:△ABC≌△DFE;
(2)若BF=20,EC=8,求BC的长.
【模型二:翻折型】
【典例2】已知,∠A=∠D,BC平分∠ABD,求证:AC=DC.
【变式2-1】如图,已知 是 的角平分线, . 求证: .
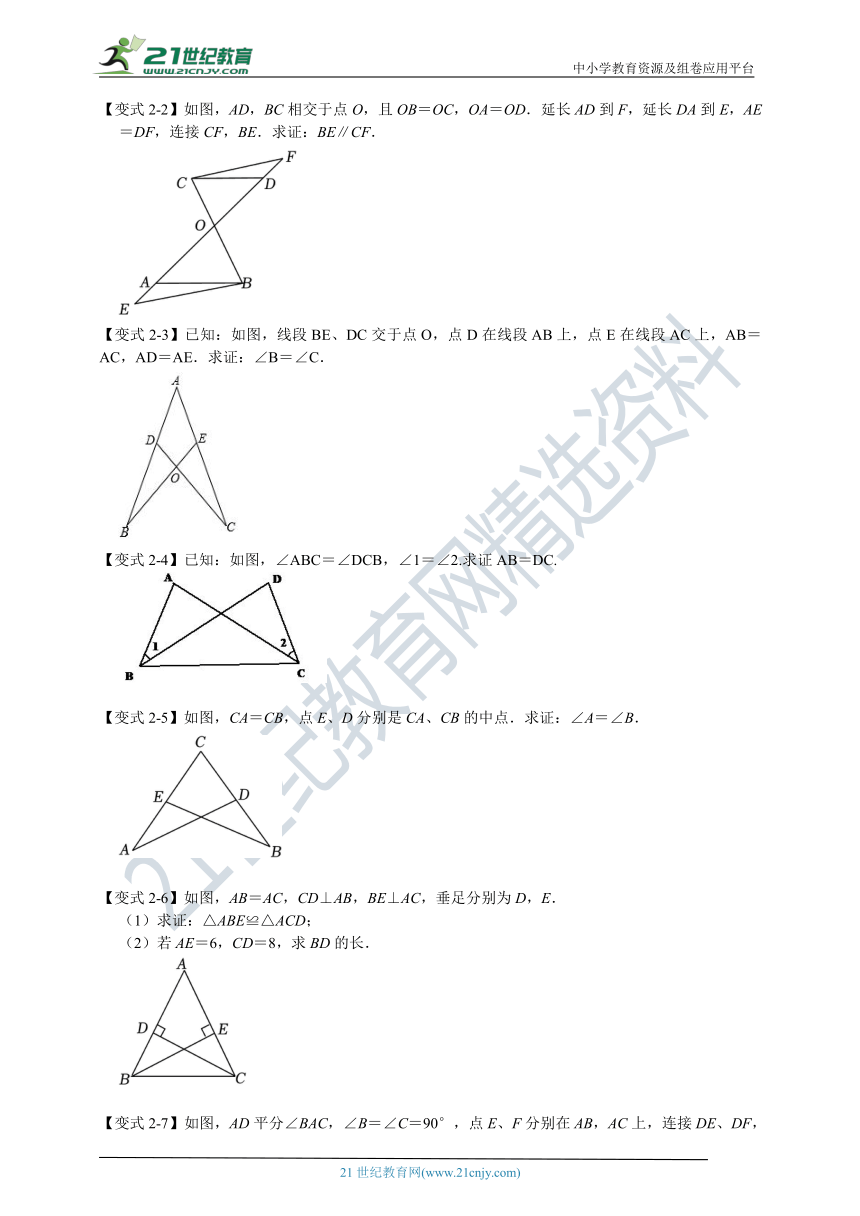
【变式2-2】如图,AD,BC相交于点O,且OB=OC,OA=OD.延长AD到F,延长DA到E,AE=DF,连接CF,BE.求证:BE∥CF.
【变式2-3】已知:如图,线段BE、DC交于点O,点D在线段AB上,点E在线段AC上,AB=AC,AD=AE.求证:∠B=∠C.
【变式2-4】已知:如图,∠ABC=∠DCB,∠1=∠2.求证AB=DC.
【变式2-5】如图,CA=CB,点E、D分别是CA、CB的中点.求证:∠A=∠B.
【变式2-6】如图,AB=AC,CD⊥AB,BE⊥AC,垂足分别为D,E.
(1)求证:△ABE≌△ACD;
(2)若AE=6,CD=8,求BD的长.
【变式2-7】如图,AD平分∠BAC,∠B=∠C=90°,点E、F分别在AB,AC上,连接DE、DF,且DE=DF.求证:AE=AF.
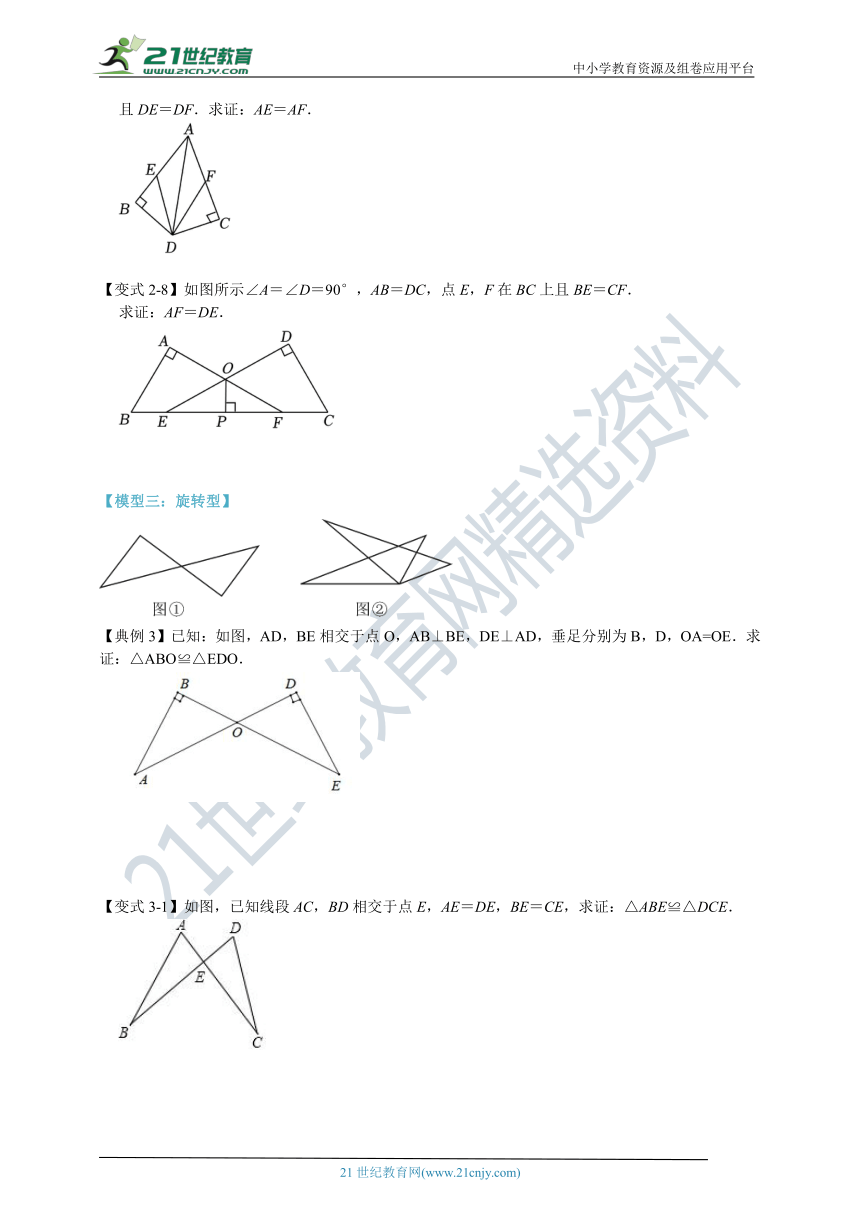
【变式2-8】如图所示∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.
求证:AF=DE.
【模型三:旋转型】
【典例3】已知:如图,AD,BE相交于点O,AB⊥BE,DE⊥AD,垂足分别为B,D,OA=OE.求证:△ABO≌△EDO.
【变式3-1】如图,已知线段AC,BD相交于点E,AE=DE,BE=CE,求证:△ABE≌△DCE.
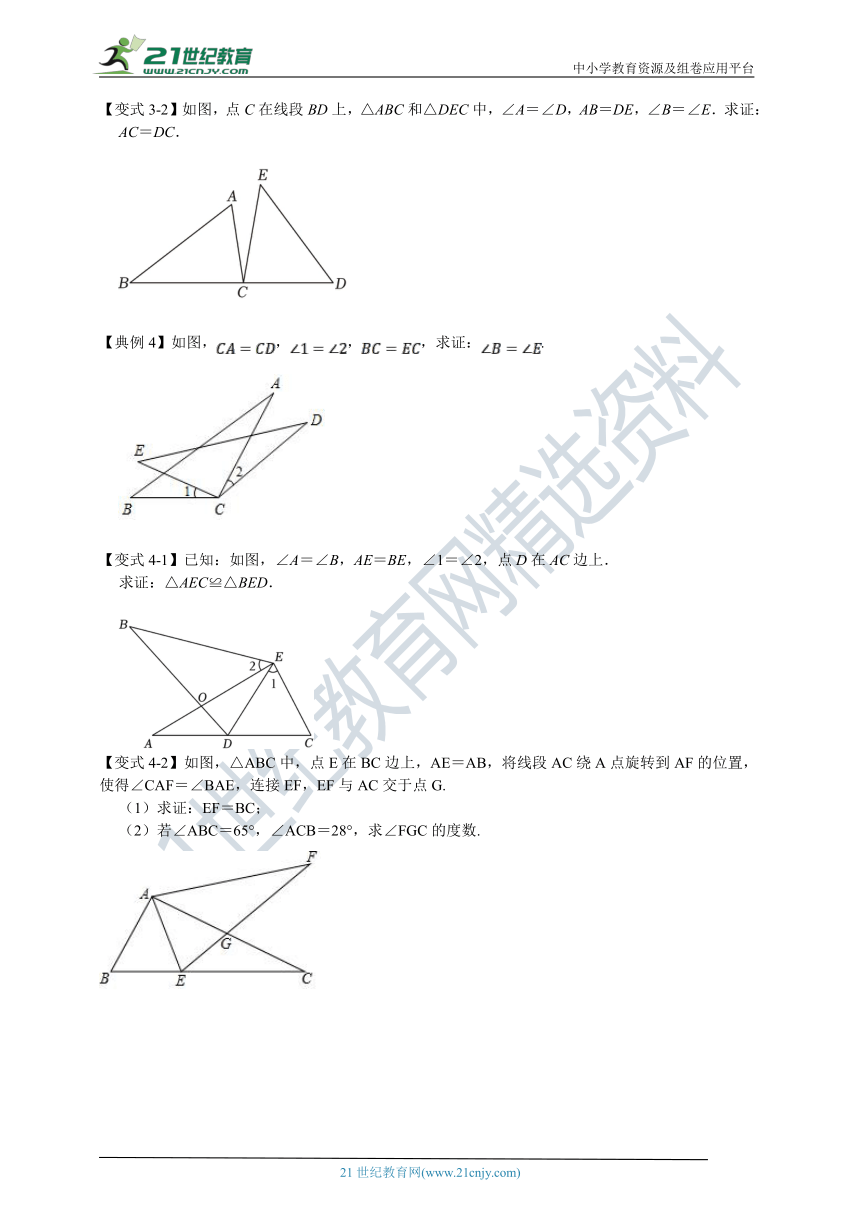
【变式3-2】如图,点C在线段BD上,△ABC和△DEC中,∠A=∠D,AB=DE,∠B=∠E.求证:AC=DC.
【典例4】如图,,,,求证:.
【变式4-1】已知:如图,∠A=∠B,AE=BE,∠1=∠2,点D在AC边上.
求证:△AEC≌△BED.
【变式4-2】如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
【变式4-3】如图,已知AB=AC,AD=AE,∠BAC=∠DAE,且B、D、E三点共线,
(1)证明:△ABD≌△ACE;
(2)证明:∠3=∠1+∠2.
【变式4-4】如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.
(1)求证:△ABD≌△EDC;
(2)若AB=2,BE=3,求CD的长.
【模型四:一线三垂直型】
【典例5】如图,AB=AC,直线l经过点A,BM⊥l,CN⊥l,垂足分别为M、N,BM=AN.
(1)求证:MN=BM+CN;
(2)求证:∠BAC=90°.
【变式5-1】王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合.
(1)求证:△ADC≌△CEB;
(2)求两堵木墙之间的距离.
【变式5-2】如图,在Rt△ABC中,∠C=90°,BE=AC,BD∥AC,DE⊥AB于点E.求证:AB=BD.
【变式5-3】如图,在△ABC中,AD是BC边上的中线,BE⊥AD于点E,CF⊥AD于点F.
(1)求证:BE=CF.
(2)若∠BAC=90°,AD=2DE,求∠BAE的度数.
【变式5-4】在 中, , ,直线 经过点 ,且 于 , 于 .
(1)当直线 绕点 旋转到图1的位置时,
①求证: ≌ ;
②求证: ;
(2)当直线 绕点 旋转到图2的位置时,(1)中的结论②还成立吗?若成立,请给出证明;若不成立,说明理由.
专题04 全等三角形基本模型(4大模型)
重难点题型归纳
【模型一:平移型】
【模型二:翻折型】
【模型三:旋转型】
【模型四:一线三垂直型】
【模型一:平移型】
【典例1】如图,已知点E、C在线段BF上, , , .求证: .
【解答】证明:
,即 .
∴在 和 中,
【变式1-1】如图,已知Rt△ABC与Rt△DEF中,∠A=∠D=90°,点B、F、C、E在同一直线上,且AB=DE,BF=CE,求证:∠B=∠E.
【解答】证明:∵,
∴
在和中
∵
∴
∴.
【变式1-2】已知:如图,点F、C在线段BE上,AB=DE,∠B=∠E,BF=EC.求证:∠A=∠D.
【解答】证明:∵BF=EC,
∴BF+CF=EC+CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠A=∠D
【变式1-3】如图,点B,C,E,F在同一直线上,,,,垂足分别为C,F,.求证:.
【解答】证明:∵,
∴即,
在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF(HL),
∴AC=DF.
【变式1-4】如图,已知点B,E,C,F在一条直线上,BE=CF,AC∥DE,∠A=∠D.
(1)求证:△ABC≌△DFE;
(2)若BF=20,EC=8,求BC的长.
【解答】(1)证明:∵AC∥DE,
∴∠ACB=∠DEF,
∵BE=CF,
∴BE+CE=CF+CE,
即BC=FE,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(AAS).
(2)解:∵BF=20,EC=8,
∴BE+CF=20﹣8=12,
∵BE=CF,
∴BE=CF=6,
∴BC=BE+EC=6+8=14.
【模型二:翻折型】
【典例2】已知,∠A=∠D,BC平分∠ABD,求证:AC=DC.
【解答】解:∵BC平分∠ABD,
∴∠ABC=∠DBC,
在△BAC和△BDC中,
∴△BAC≌△BDC,
∴AC=DC.
【变式2-1】如图,已知 是 的角平分线, .
求证: .
【解答】证明:∵ 是 的角平分线(已知),
∴ (角平分线定义),
在 与 中,
∵
∴ .
【变式2-2】如图,AD,BC相交于点O,且OB=OC,OA=OD.延长AD到F,延长DA到E,AE=DF,连接CF,BE.求证:BE∥CF.
【解答】证明:∵OA=OD,AE=DF,
∴OA+AE=OD+DF,
即OE=OF,
在△OEB与△OFC中,
,
∴△OEB≌△OFC(SAS),
∴∠E=∠F,
∴BE∥CF.
【变式2-3】已知:如图,线段BE、DC交于点O,点D在线段AB上,点E在线段AC上,AB=AC,AD=AE.求证:∠B=∠C.
【解答】解:在△AEB和△ADC中,
,
∴△AEB≌△ADC(SAS),
∴∠B=∠C.
【变式2-4】已知:如图,∠ABC=∠DCB,∠1=∠2.求证AB=DC.
【解答】证明:如图,记的交点为O,
∵∠ABC=∠DCB,∠1=∠2,
又∵∠OBC=∠ABC ∠1,∠OCB=∠DCB ∠2,
∴∠OBC=∠OCB,
∴OB=OC,
在△ABO和△DCO中,,
∴△ABO≌△DCO(ASA),
∴AB=DC.
【变式2-5】如图,CA=CB,点E、D分别是CA、CB的中点.求证:∠A=∠B.
【解答】证明:∵点E、D分别是CA、CB的中点,
∴CE=CA,CD=CB,
∵CA=CB,
∴CE=CD,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠A=∠B.
【变式2-6】如图,AB=AC,CD⊥AB,BE⊥AC,垂足分别为D,E.
(1)求证:△ABE≌△ACD;
(2)若AE=6,CD=8,求BD的长.
【解答】(1)证明:∵CD⊥AB,BE⊥AC,
∴∠AEB=∠ADC=90°,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(AAS);
(2)解:∵△ABE≌△ACD,
∴AD=AE=6,
在Rt△ACD中,AC===10,
∵AB=AC=10,
∴BD=AB﹣AD=10﹣6=4.
【变式2-7】如图,AD平分∠BAC,∠B=∠C=90°,点E、F分别在AB,AC上,连接DE、DF,且DE=DF.求证:AE=AF.
【解答】证明:∵AD平分∠BAC,
∴∠BAD=CAD,
又∵∠B=∠C=90°,AD=AD,
∴△ABD≌△ACD(AAS),
∴BD=CD,AB=AC,
在Rt△BDE与Rt△CDF,
,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF,
∴AE=AF.
【变式2-8】如图所示∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.
求证:AF=DE.
【解答】证明:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在Rt△ABF和Rt△DCE中,
,
∴Rt△ABF≌Rt△DCE(HL),
∴AF=DE.
【模型三:旋转型】
【典例3】已知:如图,AD,BE相交于点O,AB⊥BE,DE⊥AD,垂足分别为B,D,OA=OE.求证:△ABO≌△EDO.
【解答】证明:∵AB⊥BE,DE⊥AD,
∴∠B=∠D=90°.
在△ABO和△EDO中
,
∴△ABO≌△EDO.
【变式3-1】如图,已知线段AC,BD相交于点E,AE=DE,BE=CE,求证:△ABE≌△DCE.
【解答】证明:在△ABE和△DCE中 ,
∴△ABE≌△DCE(SAS)
【变式3-2】如图,点C在线段BD上,△ABC和△DEC中,∠A=∠D,AB=DE,∠B=∠E.求证:AC=DC.
【解答】解:在△ABC和△DEC中,
,
∴△ABC≌△DEC(ASA),
∴AC=DC
【典例4】如图,,,,求证:.
【解答】证明:∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA,即∠ACB=∠DCE,
在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),
∴.
【变式4-1】已知:如图,∠A=∠B,AE=BE,∠1=∠2,点D在AC边上.
求证:△AEC≌△BED.
【解答】证明:∵∠1=∠2,
∴∠AEC=∠BED,
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
【变式4-2】如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
【解答】(1)证明:∵∠CAF=∠BAE,
∴∠CAF+∠CAE=∠BAE+∠CAE,即∠EAF=∠BAC,
∵AE=AB,AC=AF,
∴△EAF≌△BAC,
∴EF=BC;
(2)解:∵△EAF≌△BAC,
∴∠AEF=∠ABC=65°,
∵AB=AE,
∴∠AEB=∠ABC=65°,
∴∠FEC=180°-∠AEB-∠AEF=50°,
∴∠FGC=∠FEC+∠ACB=78°.
【变式4-3】如图,已知AB=AC,AD=AE,∠BAC=∠DAE,且B、D、E三点共线,
(1)证明:△ABD≌△ACE;
(2)证明:∠3=∠1+∠2.
【解答】证明:(1)∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠1,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)由(1)可知,△ABD≌△ACE,
∴∠ABD=∠2,
∴∠3=∠BAD+∠ABD=∠1+∠2.
【变式4-4】如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.
(1)求证:△ABD≌△EDC;
(2)若AB=2,BE=3,求CD的长.
【解答】(1)证明:∵AB∥CD,
∴∠ABD=∠EDC.
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
(2)∵△ABD≌△EDC,
∴AB=DE=2,BD=CD,
∴CD=BD=DE+BE=2+3=5.
【模型四:一线三垂直型】
【典例5】如图,AB=AC,直线l经过点A,BM⊥l,CN⊥l,垂足分别为M、N,BM=AN.
(1)求证:MN=BM+CN;
(2)求证:∠BAC=90°.
【解答】(1)证明:∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°,
在Rt△AMB和Rt△CNA中,
,
∴Rt△AMB≌Rt△CNA(HL),
∴BM=AN,CN=AM,
∴MN=AM+AN=BM+CN;
(2)由(1)得:Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN,
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°,
∴∠BAC=180°﹣90°=90°.
【变式5-1】王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合.
(1)求证:△ADC≌△CEB;
(2)求两堵木墙之间的距离.
【解答】(1)证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS);
(2)解:由题意得:AD=2×3=6(cm),BE=7×2=14(cm),
∵△ADC≌△CEB,
∴EC=AD=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
【变式5-2】如图,在Rt△ABC中,∠C=90°,BE=AC,BD∥AC,DE⊥AB于点E.求证:AB=BD.
【解答】证明:∵∠C=90°,DE⊥AB于点E,
∴∠C=∠BED=90°,
∵BD∥AC,
∴∠A=∠DBE,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(ASA),
∴AB=BD.
【变式5-3】如图,在△ABC中,AD是BC边上的中线,BE⊥AD于点E,CF⊥AD于点F.
(1)求证:BE=CF.
(2)若∠BAC=90°,AD=2DE,求∠BAE的度数.
【解答】(1)证明:∵AD是△ABC的中线,
∴BD=CD,
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(AAS),
∴BE=CF;
(2)解:∵△BDE≌△CDF,
∴DE=DF,
∵AD=2DE,
∴DF=AF,
∵CF⊥AD,
∴AC=DC,
∴BD=DC=AC,
∴BC=2AC,
∵∠BAC=90°,
∴∠ABC=30°,
∵AD=BD,
∴∠BAE=30°.
【变式5-4】在 中, , ,直线 经过点 ,且 于 , 于 .
(1)当直线 绕点 旋转到图1的位置时,
①求证: ≌ ;
②求证: ;
(2)当直线 绕点 旋转到图2的位置时,(1)中的结论②还成立吗?若成立,请给出证明;若不成立,说明理由.
【解答】(1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
又∵AC=BC,
∴ ≌ ;
②∵ ≌ ,
∴CD=BE,AD=CE,
∵DE=CE+CD,
∴DE=AD+BE;
(2)解:DE=AD+BE不成立,此时应有DE=AD-BE,理由如下:
∵BE⊥MN,AD⊥MN,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
又∵AC=BC,
∴ ≌ ,
∴AD=CE,CD=BE,
∵DE=CE-CD,
∴DE=AD-BE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题04 全等三角形基本模型(4大模型)
重难点题型归纳
【模型一:平移型】
【模型二:翻折型】
【模型三:旋转型】
【模型四:一线三垂直型】
【模型一:平移型】
【典例1】如图,已知点E、C在线段BF上, , , .求证: .
【变式1-1】如图,已知Rt△ABC与Rt△DEF中,∠A=∠D=90°,点B、F、C、E在同一直线上,且AB=DE,BF=CE,求证:∠B=∠E.
【变式1-2】已知:如图,点F、C在线段BE上,AB=DE,∠B=∠E,BF=EC.求证:∠A=∠D.
【变式1-3】如图,点B,C,E,F在同一直线上,,,,垂足分别为C,F,.求证:.
【变式1-4】如图,已知点B,E,C,F在一条直线上,BE=CF,AC∥DE,∠A=∠D.
(1)求证:△ABC≌△DFE;
(2)若BF=20,EC=8,求BC的长.
【模型二:翻折型】
【典例2】已知,∠A=∠D,BC平分∠ABD,求证:AC=DC.
【变式2-1】如图,已知 是 的角平分线, . 求证: .
【变式2-2】如图,AD,BC相交于点O,且OB=OC,OA=OD.延长AD到F,延长DA到E,AE=DF,连接CF,BE.求证:BE∥CF.
【变式2-3】已知:如图,线段BE、DC交于点O,点D在线段AB上,点E在线段AC上,AB=AC,AD=AE.求证:∠B=∠C.
【变式2-4】已知:如图,∠ABC=∠DCB,∠1=∠2.求证AB=DC.
【变式2-5】如图,CA=CB,点E、D分别是CA、CB的中点.求证:∠A=∠B.
【变式2-6】如图,AB=AC,CD⊥AB,BE⊥AC,垂足分别为D,E.
(1)求证:△ABE≌△ACD;
(2)若AE=6,CD=8,求BD的长.
【变式2-7】如图,AD平分∠BAC,∠B=∠C=90°,点E、F分别在AB,AC上,连接DE、DF,且DE=DF.求证:AE=AF.
【变式2-8】如图所示∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.
求证:AF=DE.
【模型三:旋转型】
【典例3】已知:如图,AD,BE相交于点O,AB⊥BE,DE⊥AD,垂足分别为B,D,OA=OE.求证:△ABO≌△EDO.
【变式3-1】如图,已知线段AC,BD相交于点E,AE=DE,BE=CE,求证:△ABE≌△DCE.
【变式3-2】如图,点C在线段BD上,△ABC和△DEC中,∠A=∠D,AB=DE,∠B=∠E.求证:AC=DC.
【典例4】如图,,,,求证:.
【变式4-1】已知:如图,∠A=∠B,AE=BE,∠1=∠2,点D在AC边上.
求证:△AEC≌△BED.
【变式4-2】如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
【变式4-3】如图,已知AB=AC,AD=AE,∠BAC=∠DAE,且B、D、E三点共线,
(1)证明:△ABD≌△ACE;
(2)证明:∠3=∠1+∠2.
【变式4-4】如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.
(1)求证:△ABD≌△EDC;
(2)若AB=2,BE=3,求CD的长.
【模型四:一线三垂直型】
【典例5】如图,AB=AC,直线l经过点A,BM⊥l,CN⊥l,垂足分别为M、N,BM=AN.
(1)求证:MN=BM+CN;
(2)求证:∠BAC=90°.
【变式5-1】王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合.
(1)求证:△ADC≌△CEB;
(2)求两堵木墙之间的距离.
【变式5-2】如图,在Rt△ABC中,∠C=90°,BE=AC,BD∥AC,DE⊥AB于点E.求证:AB=BD.
【变式5-3】如图,在△ABC中,AD是BC边上的中线,BE⊥AD于点E,CF⊥AD于点F.
(1)求证:BE=CF.
(2)若∠BAC=90°,AD=2DE,求∠BAE的度数.
【变式5-4】在 中, , ,直线 经过点 ,且 于 , 于 .
(1)当直线 绕点 旋转到图1的位置时,
①求证: ≌ ;
②求证: ;
(2)当直线 绕点 旋转到图2的位置时,(1)中的结论②还成立吗?若成立,请给出证明;若不成立,说明理由.
专题04 全等三角形基本模型(4大模型)
重难点题型归纳
【模型一:平移型】
【模型二:翻折型】
【模型三:旋转型】
【模型四:一线三垂直型】
【模型一:平移型】
【典例1】如图,已知点E、C在线段BF上, , , .求证: .
【解答】证明:
,即 .
∴在 和 中,
【变式1-1】如图,已知Rt△ABC与Rt△DEF中,∠A=∠D=90°,点B、F、C、E在同一直线上,且AB=DE,BF=CE,求证:∠B=∠E.
【解答】证明:∵,
∴
在和中
∵
∴
∴.
【变式1-2】已知:如图,点F、C在线段BE上,AB=DE,∠B=∠E,BF=EC.求证:∠A=∠D.
【解答】证明:∵BF=EC,
∴BF+CF=EC+CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠A=∠D
【变式1-3】如图,点B,C,E,F在同一直线上,,,,垂足分别为C,F,.求证:.
【解答】证明:∵,
∴即,
在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF(HL),
∴AC=DF.
【变式1-4】如图,已知点B,E,C,F在一条直线上,BE=CF,AC∥DE,∠A=∠D.
(1)求证:△ABC≌△DFE;
(2)若BF=20,EC=8,求BC的长.
【解答】(1)证明:∵AC∥DE,
∴∠ACB=∠DEF,
∵BE=CF,
∴BE+CE=CF+CE,
即BC=FE,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(AAS).
(2)解:∵BF=20,EC=8,
∴BE+CF=20﹣8=12,
∵BE=CF,
∴BE=CF=6,
∴BC=BE+EC=6+8=14.
【模型二:翻折型】
【典例2】已知,∠A=∠D,BC平分∠ABD,求证:AC=DC.
【解答】解:∵BC平分∠ABD,
∴∠ABC=∠DBC,
在△BAC和△BDC中,
∴△BAC≌△BDC,
∴AC=DC.
【变式2-1】如图,已知 是 的角平分线, .
求证: .
【解答】证明:∵ 是 的角平分线(已知),
∴ (角平分线定义),
在 与 中,
∵
∴ .
【变式2-2】如图,AD,BC相交于点O,且OB=OC,OA=OD.延长AD到F,延长DA到E,AE=DF,连接CF,BE.求证:BE∥CF.
【解答】证明:∵OA=OD,AE=DF,
∴OA+AE=OD+DF,
即OE=OF,
在△OEB与△OFC中,
,
∴△OEB≌△OFC(SAS),
∴∠E=∠F,
∴BE∥CF.
【变式2-3】已知:如图,线段BE、DC交于点O,点D在线段AB上,点E在线段AC上,AB=AC,AD=AE.求证:∠B=∠C.
【解答】解:在△AEB和△ADC中,
,
∴△AEB≌△ADC(SAS),
∴∠B=∠C.
【变式2-4】已知:如图,∠ABC=∠DCB,∠1=∠2.求证AB=DC.
【解答】证明:如图,记的交点为O,
∵∠ABC=∠DCB,∠1=∠2,
又∵∠OBC=∠ABC ∠1,∠OCB=∠DCB ∠2,
∴∠OBC=∠OCB,
∴OB=OC,
在△ABO和△DCO中,,
∴△ABO≌△DCO(ASA),
∴AB=DC.
【变式2-5】如图,CA=CB,点E、D分别是CA、CB的中点.求证:∠A=∠B.
【解答】证明:∵点E、D分别是CA、CB的中点,
∴CE=CA,CD=CB,
∵CA=CB,
∴CE=CD,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠A=∠B.
【变式2-6】如图,AB=AC,CD⊥AB,BE⊥AC,垂足分别为D,E.
(1)求证:△ABE≌△ACD;
(2)若AE=6,CD=8,求BD的长.
【解答】(1)证明:∵CD⊥AB,BE⊥AC,
∴∠AEB=∠ADC=90°,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(AAS);
(2)解:∵△ABE≌△ACD,
∴AD=AE=6,
在Rt△ACD中,AC===10,
∵AB=AC=10,
∴BD=AB﹣AD=10﹣6=4.
【变式2-7】如图,AD平分∠BAC,∠B=∠C=90°,点E、F分别在AB,AC上,连接DE、DF,且DE=DF.求证:AE=AF.
【解答】证明:∵AD平分∠BAC,
∴∠BAD=CAD,
又∵∠B=∠C=90°,AD=AD,
∴△ABD≌△ACD(AAS),
∴BD=CD,AB=AC,
在Rt△BDE与Rt△CDF,
,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF,
∴AE=AF.
【变式2-8】如图所示∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.
求证:AF=DE.
【解答】证明:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在Rt△ABF和Rt△DCE中,
,
∴Rt△ABF≌Rt△DCE(HL),
∴AF=DE.
【模型三:旋转型】
【典例3】已知:如图,AD,BE相交于点O,AB⊥BE,DE⊥AD,垂足分别为B,D,OA=OE.求证:△ABO≌△EDO.
【解答】证明:∵AB⊥BE,DE⊥AD,
∴∠B=∠D=90°.
在△ABO和△EDO中
,
∴△ABO≌△EDO.
【变式3-1】如图,已知线段AC,BD相交于点E,AE=DE,BE=CE,求证:△ABE≌△DCE.
【解答】证明:在△ABE和△DCE中 ,
∴△ABE≌△DCE(SAS)
【变式3-2】如图,点C在线段BD上,△ABC和△DEC中,∠A=∠D,AB=DE,∠B=∠E.求证:AC=DC.
【解答】解:在△ABC和△DEC中,
,
∴△ABC≌△DEC(ASA),
∴AC=DC
【典例4】如图,,,,求证:.
【解答】证明:∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA,即∠ACB=∠DCE,
在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),
∴.
【变式4-1】已知:如图,∠A=∠B,AE=BE,∠1=∠2,点D在AC边上.
求证:△AEC≌△BED.
【解答】证明:∵∠1=∠2,
∴∠AEC=∠BED,
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
【变式4-2】如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
【解答】(1)证明:∵∠CAF=∠BAE,
∴∠CAF+∠CAE=∠BAE+∠CAE,即∠EAF=∠BAC,
∵AE=AB,AC=AF,
∴△EAF≌△BAC,
∴EF=BC;
(2)解:∵△EAF≌△BAC,
∴∠AEF=∠ABC=65°,
∵AB=AE,
∴∠AEB=∠ABC=65°,
∴∠FEC=180°-∠AEB-∠AEF=50°,
∴∠FGC=∠FEC+∠ACB=78°.
【变式4-3】如图,已知AB=AC,AD=AE,∠BAC=∠DAE,且B、D、E三点共线,
(1)证明:△ABD≌△ACE;
(2)证明:∠3=∠1+∠2.
【解答】证明:(1)∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠1,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)由(1)可知,△ABD≌△ACE,
∴∠ABD=∠2,
∴∠3=∠BAD+∠ABD=∠1+∠2.
【变式4-4】如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.
(1)求证:△ABD≌△EDC;
(2)若AB=2,BE=3,求CD的长.
【解答】(1)证明:∵AB∥CD,
∴∠ABD=∠EDC.
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
(2)∵△ABD≌△EDC,
∴AB=DE=2,BD=CD,
∴CD=BD=DE+BE=2+3=5.
【模型四:一线三垂直型】
【典例5】如图,AB=AC,直线l经过点A,BM⊥l,CN⊥l,垂足分别为M、N,BM=AN.
(1)求证:MN=BM+CN;
(2)求证:∠BAC=90°.
【解答】(1)证明:∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°,
在Rt△AMB和Rt△CNA中,
,
∴Rt△AMB≌Rt△CNA(HL),
∴BM=AN,CN=AM,
∴MN=AM+AN=BM+CN;
(2)由(1)得:Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN,
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°,
∴∠BAC=180°﹣90°=90°.
【变式5-1】王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合.
(1)求证:△ADC≌△CEB;
(2)求两堵木墙之间的距离.
【解答】(1)证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS);
(2)解:由题意得:AD=2×3=6(cm),BE=7×2=14(cm),
∵△ADC≌△CEB,
∴EC=AD=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
【变式5-2】如图,在Rt△ABC中,∠C=90°,BE=AC,BD∥AC,DE⊥AB于点E.求证:AB=BD.
【解答】证明:∵∠C=90°,DE⊥AB于点E,
∴∠C=∠BED=90°,
∵BD∥AC,
∴∠A=∠DBE,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(ASA),
∴AB=BD.
【变式5-3】如图,在△ABC中,AD是BC边上的中线,BE⊥AD于点E,CF⊥AD于点F.
(1)求证:BE=CF.
(2)若∠BAC=90°,AD=2DE,求∠BAE的度数.
【解答】(1)证明:∵AD是△ABC的中线,
∴BD=CD,
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(AAS),
∴BE=CF;
(2)解:∵△BDE≌△CDF,
∴DE=DF,
∵AD=2DE,
∴DF=AF,
∵CF⊥AD,
∴AC=DC,
∴BD=DC=AC,
∴BC=2AC,
∵∠BAC=90°,
∴∠ABC=30°,
∵AD=BD,
∴∠BAE=30°.
【变式5-4】在 中, , ,直线 经过点 ,且 于 , 于 .
(1)当直线 绕点 旋转到图1的位置时,
①求证: ≌ ;
②求证: ;
(2)当直线 绕点 旋转到图2的位置时,(1)中的结论②还成立吗?若成立,请给出证明;若不成立,说明理由.
【解答】(1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
又∵AC=BC,
∴ ≌ ;
②∵ ≌ ,
∴CD=BE,AD=CE,
∵DE=CE+CD,
∴DE=AD+BE;
(2)解:DE=AD+BE不成立,此时应有DE=AD-BE,理由如下:
∵BE⊥MN,AD⊥MN,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
又∵AC=BC,
∴ ≌ ,
∴AD=CE,CD=BE,
∵DE=CE-CD,
∴DE=AD-BE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
