八上第一章三角形的初步知识专题-专题05全等三角形重难点模型(五大模型)(含解析)
文档属性
| 名称 | 八上第一章三角形的初步知识专题-专题05全等三角形重难点模型(五大模型)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 11:23:07 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专题05 全等三角形重难点模型(五大模型)
重难点题型归纳
【模型一:一线三等角型】
【模型二:手拉手模型】
【模型三:半角模型】
【模型四:对角互补模型】
【模型五:平行+线段中点构造全等模型】
【模型一:一线三等角型】
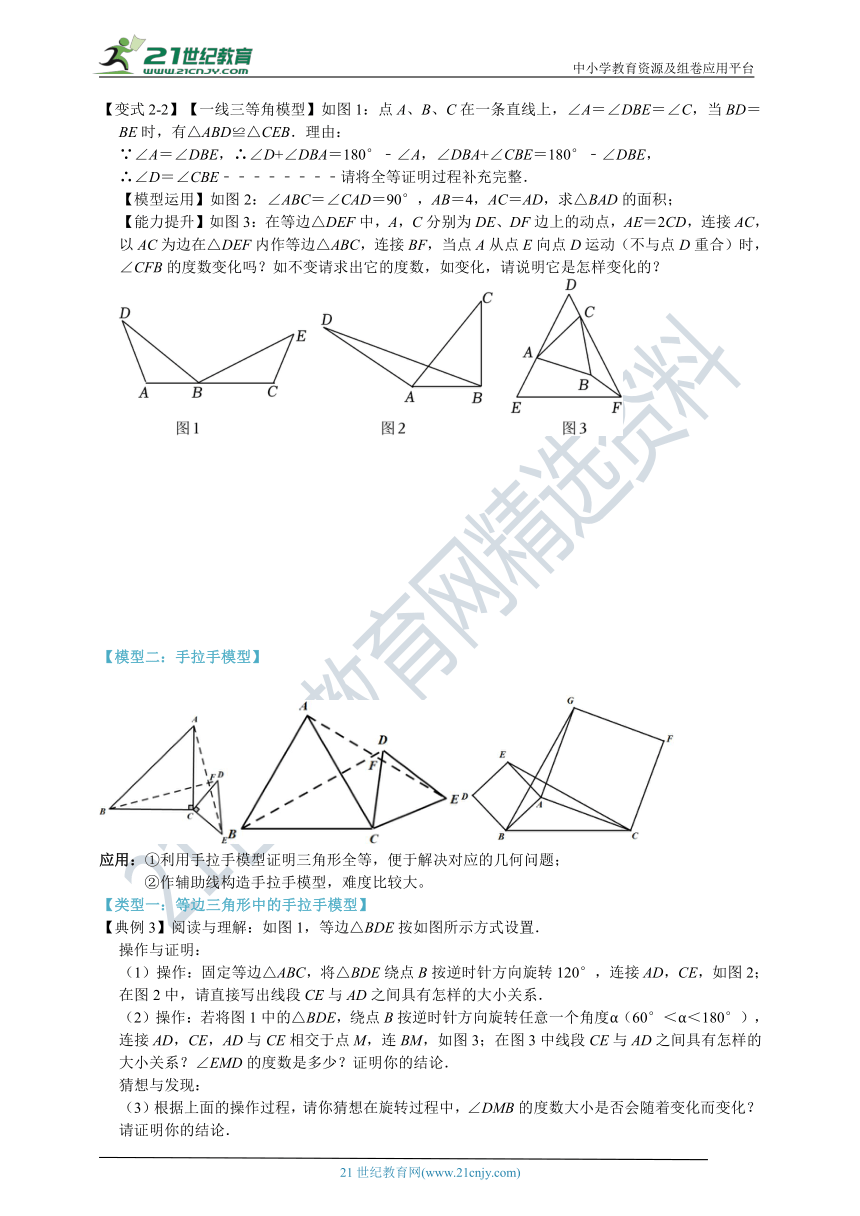
如图一,∠D=∠BCA=∠E=90°,BC=AC。 结论:Rt△BDC≌Rt△CEA
模型二 一线三等角全等模型
如图二,∠D=∠BCA=∠E,BC=AC。 结论:△BEC≌△CDA
图一 图二
应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;
②与函数综合应用中有利于点的坐标的求解。
【典例1】如图,平面直角坐标系中有点A(﹣1,0)和y轴上一动点B(0,a),其中a>0,以B点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).
(1)当a=2时,则C点的坐标为 ;
(2)动点B在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.
【变式1-1】如图,在△PMN中,PM=PN,PM⊥PN,P(0,2),N(2,﹣2),则M的坐标是( )
A.(﹣2,0) B.(﹣2,0) C.(﹣2,0) D.(﹣4,0)
【变式1-2】在学习完“探索全等三角形全等的条件”一节后,一同学总结出很多全等三角形的模型,他设计了以下问题给同桌解决:如图,做一个“U”字形框架PABQ,其中AB=42cm,AP,BQ足够长,PA⊥AB于点A,点M从B出发向A运动,同时点N从B出发向Q运动,点M,N运动的速度之比为3:4,当两点运动到某一瞬间同时停止,此时在射线AP上取点C,使△ACM与△BMN全等,则线段AC的长为 cm.
【变式1-3】阅读理解,自主探究:
“一线三垂直”模型是“一线三等角”模型的特殊情况,即三个等角角度为90°,于是有三组边相互垂直.所以称为“一线三垂直模型”.当模型中有一组对应边长相等时,则模型中必定存在全等三角形.
(1)问题解决:如图1,在等腰直角△ABC中,∠ACB=90°,AC=BC,过点C作直线DE,AD⊥DE于D,BE⊥DE于E,求证:△ADC≌△CEB;
(2)问题探究:如图2,在等腰直角△ABC中,∠ACB=90°,AC=BC,过点C作直线CE,AD⊥CE于D,BE⊥CE于E,AD=2.5cm,DE=1.7cm,求BE的长;
(3)拓展延伸:如图3,在平面直角坐标系中,A(﹣1,0),C(1,3),△ABC为等腰直角三角形,∠ACB=90°,AC=BC,求B点坐标.
【典例2】(1)猜想:如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.试猜想DE、BD、CE有怎样的数量关系,请直接写出;
(2)探究:如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α(其中α为任意锐角或钝角)如果成立,请你给出证明;若不成立,请说明理由;
(3)解决问题:如图3,F是角平分线上的一点,且△ABF和△ACF均为等边三角形,D、E分别是直线m上A点左右两侧的动点,D、E、A互不重合,在运动过程中线段DE的长度始终为n,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并说明理由.
【变式2-1】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
【变式2-2】【一线三等角模型】如图1:点A、B、C在一条直线上,∠A=∠DBE=∠C,当BD=BE时,有△ABD≌△CEB.理由:
∵∠A=∠DBE,∴∠D+∠DBA=180°﹣∠A,∠DBA+∠CBE=180°﹣∠DBE,
∴∠D=∠CBE﹣﹣﹣﹣﹣﹣﹣﹣请将全等证明过程补充完整.
【模型运用】如图2:∠ABC=∠CAD=90°,AB=4,AC=AD,求△BAD的面积;
【能力提升】如图3:在等边△DEF中,A,C分别为DE、DF边上的动点,AE=2CD,连接AC,以AC为边在△DEF内作等边△ABC,连接BF,当点A从点E向点D运动(不与点D重合)时,∠CFB的度数变化吗?如不变请求出它的度数,如变化,请说明它是怎样变化的?
【模型二:手拉手模型】
应用:①利用手拉手模型证明三角形全等,便于解决对应的几何问题;
②作辅助线构造手拉手模型,难度比较大。
【类型一:等边三角形中的手拉手模型】
【典例3】阅读与理解:如图1,等边△BDE按如图所示方式设置.
操作与证明:
(1)操作:固定等边△ABC,将△BDE绕点B按逆时针方向旋转120°,连接AD,CE,如图2;在图2中,请直接写出线段CE与AD之间具有怎样的大小关系.
(2)操作:若将图1中的△BDE,绕点B按逆时针方向旋转任意一个角度α(60°<α<180°),连接AD,CE,AD与CE相交于点M,连BM,如图3;在图3中线段CE与AD之间具有怎样的大小关系?∠EMD的度数是多少?证明你的结论.
猜想与发现:
(3)根据上面的操作过程,请你猜想在旋转过程中,∠DMB的度数大小是否会随着变化而变化?请证明你的结论.
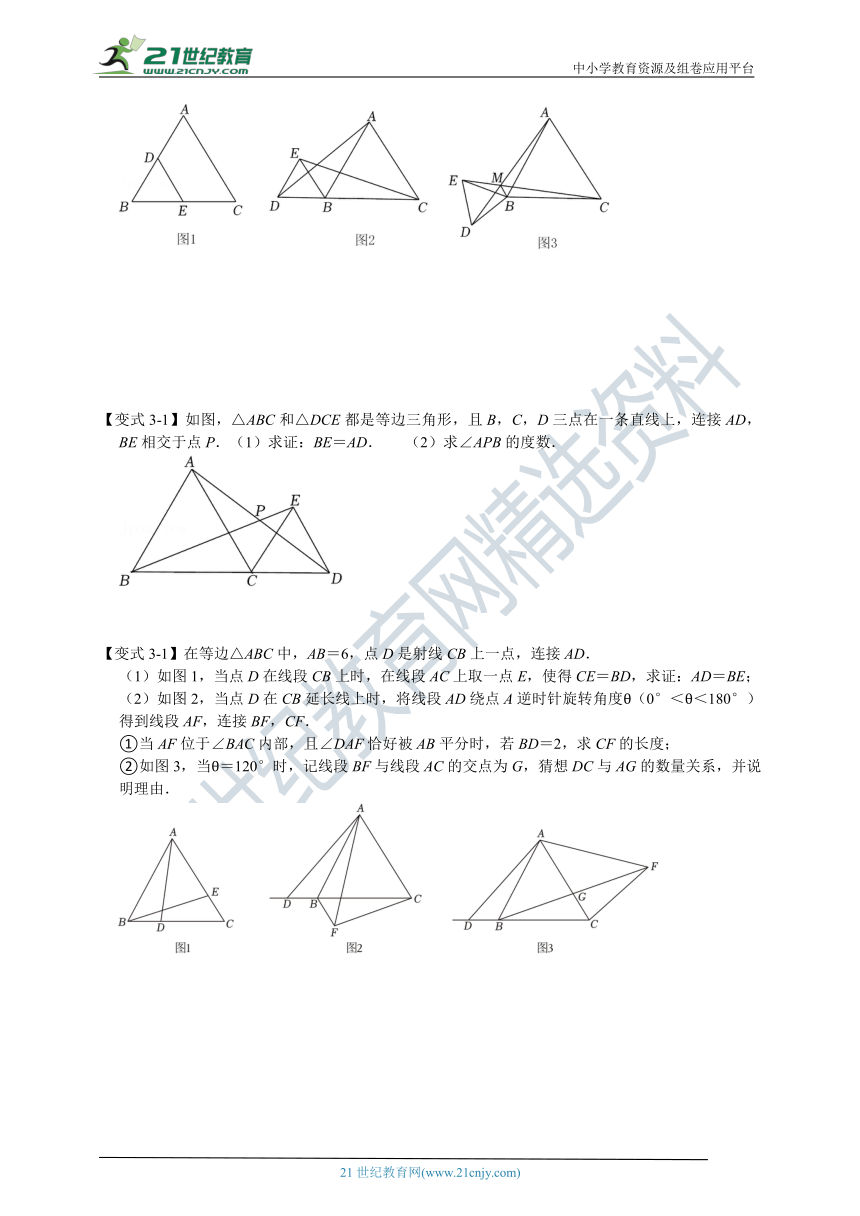
【变式3-1】如图,△ABC和△DCE都是等边三角形,且B,C,D三点在一条直线上,连接AD,BE相交于点P.(1)求证:BE=AD. (2)求∠APB的度数.
【变式3-1】在等边△ABC中,AB=6,点D是射线CB上一点,连接AD.
(1)如图1,当点D在线段CB上时,在线段AC上取一点E,使得CE=BD,求证:AD=BE;
(2)如图2,当点D在CB延长线上时,将线段AD绕点A逆时针旋转角度θ(0°<θ<180°)得到线段AF,连接BF,CF.
①当AF位于∠BAC内部,且∠DAF恰好被AB平分时,若BD=2,求CF的长度;
②如图3,当θ=120°时,记线段BF与线段AC的交点为G,猜想DC与AG的数量关系,并说明理由.
【类型二:等腰三角形的手拉手模型】
【典例4】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上时,∠BAC=90°,
①求证:BD=CE;
②∠BCE= ;
(2)设∠BCE=a,∠BAC=β,
①如图2,当点D在线段BC上移动,求证α+β=180°;
②当点D在射线BC的反向延长线上移动,则a、β之间有怎样的数量关系?请直接写出你的结论.
【变式4-1】如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N.
证明:(1)BD=CE;(2)BD⊥CE.
【变式4-2】如图,在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点,连接AD,以AD为直角边作等腰直角三角形ADF.
(1)如图1,若当点D在线段BC上时(不与点B、C重合),证明:△ACF≌△ABD;
(2)如图2,当点D在线段BC的延长线上时,试猜想CF与BD的数量关系和位置关系,并说明理由.
【变式4-3】(1)如图1,△ABC与△ADE均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:BD=CE;
(2)如图2,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
填空:∠AEB的度数为 ;线段BE与AD之间的数量关系是 .
(3)拓展探究
如图3,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
【模型二:直角三角形中的手拉手模型】
【典例5】△ABC与△BDE均为等腰直角三角形,∠ABC=∠DBE=90°.
(1)如图1,当D,B,C在同一直线时,CE的延长线与AD交于点F.求证:∠CFA=90°;
(2)当△ABC与△BDE的位置如图2时,CE的延长线与AD交于点F,猜想∠CFA的大小并证明你的结论;
(3)如图3,当A,E,D在同一直线时(A,D在点E的异侧),CE与AB交于点G,∠BAD=∠ACE,求证:BG+AB=AC.
【变式5】如图:已知△ABC中,∠BAC=90°,AB=AC,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作△ADE,使∠DAE=90°,AD=AE,连接CE.
发现问题:
如图1,当点D在边BC上时,
(1)请写出BD和CE之间的位置关系为 ,并猜想BC和CE、CD之间的数量关系: .
(2)如图2,当点D在边BC的延长线上且其他条件不变时,(1)中BD和CE之间的位置关系;BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
【模型三:作辅助线构造手拉手模型】
【典例6】在△ABC中,AB=AC,∠ABC=α,点D是直线BC上一点,点C关于射线AD的对称点为点E.作直线BE交射线AD于点F.连接CF.
(1)如图1,点D在线段BC上,补全图形,求∠AFB的大小(用含α的代数式表示);
(2)如果∠α=60°,
①如图2,当点D在线段BC上时,用等式表示线段AF,BF,CF之间的数量关系,并证明;
②如图3,当点D在线段CB的延长线上时,直接写出线段AF、BF、CF之间的数量关系.
【变式6-1】已知,∠MON=90°,点A在边OM上,点P是边ON上一动点,∠OAP=α.以线段AP为边在AP上方作等边△ABP,连接OB、BP,再以线段OB为边作等边△OBC(点C、P在OB的同侧),作CH⊥ON于点H.
(1)如图1,α=60°.①依题意补全图形;②求∠BPH的度数;
(2)如图2,当点P在射线ON上运动时,用等式表示线段OA与CH之间的数量关系,并证明.
【模型三:半角模型】等角=要三角形中得半角模型
【典例7】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.已知,△ABC中,AB=AC,∠BAC=α,点D、E在边BC上,且EF=.
(1)如图a,当α=60°时,将△AEC绕点A顺时针旋转60°到△AFB的位置,连结DF.
①∠DAF= ;②求证:DF=DE;
(2)如图b,当α=90°时,猜想BD、DE、CE的数量关系,并说明理由.
【变式7-1】已知∠MBN=60°,等边△BEF与∠MBN顶点B重合,将等边△BEF绕顶点B顺时针旋转,边EF所在直线与∠MBN的BN边相交于点C,并在BM边上截取AB=BC,连接AE.
(1)将等边△BEF旋转至如图①所示位置时,求证:CE=BE+AE;
(2)将等边△BEF顺时针旋转至如图②、图③位置时,请分别直接写出AE,BE,CE之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若BF=4,AE=1,则CE= .
【变式7-2】如图,△ABC是等边三角形,D是边BC上一点(点D不与点B,C重合),作∠EDF=60°,使角的两边分别交边AB,AC于点E,F,且BD=CF.
(1)如图①,若DE⊥BC,则∠DFC= 度;
(2)如图②,D是边BC上一点(点D不与点B,C重合),求证:BE=CD;
(3)如图③,若D是边BC的中点,且AB=2,则四边形AEDF的周长为 .
【变式7-3】】等边△ABC,D为△ABC外一点,∠BDC=120°,BD=DC,∠MDN=60°,射线DM与直线AB相交于点M,射线DN与直线AC相交于点N,
①当点M、N在边AB、AC上,且DM=DN时,直接写出BM、NC、MN之间的数量关系.
②当点M、N在边AB、AC上,且DM≠DN时,猜想①中的结论还成立吗?若成立,请证明.
③当点M、N在边AB、CA的延长线上时,请画出图形,并写出BM、NC、MN之间的数量关系.
【模型四:对角互补模型】
应用:通过做垂线或者利用旋转构造全等三角形解决问题。
【典例9】(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图(2),在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
【变式9-1】【教材呈现】如图是华师版八年级上册数学教材96页的部分内容.
已知:如图13.5.4,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为点D和点E.求证:PD=PE.分析:图中有两个直角三角形PDO和PEO,只要证明这两个三角形全等便可证得PD=PE.
【问题解决】请根据教材分析,结合图①写出证明PD=PE的过程.
【类比探究】
(1)如图②,OC是∠AOB的平分线,P是OC上任意一点,点M,N分别在OB和OA上,连接PM和PN,若∠PMO+∠PNO=180°,求证:PM=PN;
(2)如图③,△ABC的周长是12,BO、CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若OD=3,则△ABC的面积为 .
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2023/7/13 12:18:00;用户:gaga;邮箱:18376708956;学号:18
【变式9-2】(1)阅读理解:
如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:
延长AD到点E使DE=AD,再连接BE,这样就把AB,AC,2AD集中在△ABE中,利用三角形三边的关系可判断线段AE的取值范围是 ;则中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,此时:BE+CF EF(填“>”或“=”或“<”);
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180,CB=CD,∠BCD=140°,以C为顶点作∠ECF=70°,边CE,CF分别交AB,AD于E,F两点,连接EF,此时:BE+DF EF(填“>”或“=”或“<“);
(4)若在图③的四边形ABCD中,∠ECF=α(0°<α<90°),∠B+∠D=180,CB=CD,且(3)中的结论仍然成立,则∠BCD= (用含α的代数式表示).
【典例10】(1)如图1,四边形ABCD是边长为5 cm的正方形,E,F分别在AD,CD边上,∠EBF=45°.为了求出△DEF的周长.小南同学的探究方法是:
如图2,延长EA到H,使AH=CF,连接BH,先证△ABH≌△CBF,再证△EBH≌△EBF,得EF=EH,从而得到△DEF的周长= cm;
(2)如图3,在四边形ABCD中,AB=AD,∠BAD=100°,∠B=∠ADC=90°.E,F分别是线段BC,CD上的点.且∠EAF=50°.探究图中线段EF,BE,FD之间的数量关系;
(3)如图4,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是线段BC,CD上的点,且2∠EAF=∠BAD,(2)中的结论是否仍然成立,若成立,请证明,若不成立,请说明理由;
(4)若在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别在CB、DC的延长线上,且2∠EAF=∠BAD,请画出图形,并直接写出线段EF、BE、FD之间的数量关系.
【变式10-1】如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,求证:EF=BE+FD.
【变式10-2】“截长补短法”证明线段的和差问题:
先阅读背景材料,猜想结论并填空,然后做问题探究.
背景材料:
(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.探究的方法是,延长FD到点G.使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出的结论是 .
探索问题:
(2)如图2,若四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立?成立的话,请写出推理过程.
【模型五:平行+线段中点构造全等模型】
【结论】如图,AB∥CD,点E、F分别在直线AB、CD上,点O为EF中点,则△POE≌△QOF
口诀:有中点,有平行,轻轻延长就能行
【典例11】已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图③.写出AF、EF与AB的数量关系,并对图②进行证明.
【变式11-1】如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA⊥OC.
(1)求证:CO平分∠ACD;
(2)求证:AB+CD=AC.
【变式11-2】如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,求证AD和BC的关系。
【变式11-3】(2023春 青秀区校级期末)已知平行四边形ABCD,E为BC边上的中点.
(1)如图1,若BC=2CD,求证:DE平分∠ADC;
(2)若F为AB边上一点,连结DF,EF;
①如图2,若S△EFB=1,S△CDE=4,求S△DEF;
②如图3,若∠EFB+∠CDE=90°,请你写出线段AF,BF,DF之间的数量关系,并证明.
专题05 全等三角形重难点模型(五大模型)
重难点题型归纳
【模型一:一线三等角型】
【模型二:手拉手模型】
【模型三:半角模型】
【模型四:对角互补模型】
【模型五:平行+线段中点构造全等模型】
【模型一:一线三等角型】
如图一,∠D=∠BCA=∠E=90°,BC=AC。 结论:Rt△BDC≌Rt△CEA
模型二 一线三等角全等模型
如图二,∠D=∠BCA=∠E,BC=AC。 结论:△BEC≌△CDA
图一 图二
应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;
②与函数综合应用中有利于点的坐标的求解。
【典例1】如图,平面直角坐标系中有点A(﹣1,0)和y轴上一动点B(0,a),其中a>0,以B点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).
(1)当a=2时,则C点的坐标为 ;
(2)动点B在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.
【解答】解:(1)如图1中,过点C作CE⊥y轴于E,则∠CEB=∠AOB.
∵△ABC是等腰直角三角形,
∴BC=BA,∠ABC=90°,
∴∠BCE+∠CBE=90°=∠BAO+∠CBE,
∴∠BCE=∠ABO,
在△BCE和△BAO中,
,
∴△CBE≌△BAO(AAS),
∵A(﹣1,0),B(0,2),
∴AO=BE=1,OB=CE=2,
∴OE=1+2=3,
∴C(﹣2,3),
故答案为:(﹣2,3);
(2)动点A在运动的过程中,c+d的值不变.
理由:过点C作CE⊥y轴于E,则∠CEA=∠AOB,
∵△ABC是等腰直角三角形,
∴BC=BA,∠ABC=90°,
∴∠BCE+∠CBE=90°=∠ABO+∠CBE,
∴∠BCE=∠ABO,
在△BCE和△BAO中,
,
∴△CBE≌△BAO(AAS),
∵B(﹣1,0),A(0,a),
∴BO=AE=1,AO=CE=a,
∴OE=1+a,
∴C(﹣a,1+a),
又∵点C的坐标为(c,d),
∴c+d=﹣a+1+a=1,
即c+d的值不变.
【变式1-1】(2021秋 鼓楼区校级期末)如图,在△PMN中,PM=PN,PM⊥PN,P(0,2),N(2,﹣2),则M的坐标是( )
A.(﹣2,0) B.(﹣2,0) C.(﹣2,0) D.(﹣4,0)
【答案】D
【解答】解:过点N作ND⊥y轴于点D,
∵P(0,2),N(2,﹣2),
∴OP=2,OD=2,DN=2,
∴PD=4,
∵PM⊥PN,
∴∠MPN=90°,
∴∠MPO+∠DPN=90°,
又∵∠DPN+∠PND=90°,
∴∠MPO=∠PND,
又∵∠MOP=∠PDN=90°,
∴△MOP≌△PDN(AAS),
∴OM=PD=4,
∴M(﹣4,0),
故选:D.
【变式1-2】(2022春 金牛区校级期中)在学习完“探索全等三角形全等的条件”一节后,一同学总结出很多全等三角形的模型,他设计了以下问题给同桌解决:如图,做一个“U”字形框架PABQ,其中AB=42cm,AP,BQ足够长,PA⊥AB于点A,点M从B出发向A运动,同时点N从B出发向Q运动,点M,N运动的速度之比为3:4,当两点运动到某一瞬间同时停止,此时在射线AP上取点C,使△ACM与△BMN全等,则线段AC的长为 18或28 cm.
【答案】18或28.
【解答】解:设BM=3tcm,则BN=4tcm,因为∠A=∠B=90°,使△ACM与△BMN全等,可分两种情况:
情况一:当BM=AC,BN=AM时,
∵BN=AM,AB=42cm,
∴4t=42﹣3t,
解得:t=6,
∴AC=BM=3t=3×6=18cm;
情况二:当BM=AM,BN=AC时,
∵BM=AM,AB=42cm,
∴3t=42﹣3t,
解得:t=7,
∴AC=BN=4t=4×7=28cm,
综上所述,AC=18cm或AC=28cm.
【变式1-3】(2022秋 青云谱区期末)阅读理解,自主探究:
“一线三垂直”模型是“一线三等角”模型的特殊情况,即三个等角角度为90°,于是有三组边相互垂直.所以称为“一线三垂直模型”.当模型中有一组对应边长相等时,则模型中必定存在全等三角形.
(1)问题解决:如图1,在等腰直角△ABC中,∠ACB=90°,AC=BC,过点C作直线DE,AD⊥DE于D,BE⊥DE于E,求证:△ADC≌△CEB;
(2)问题探究:如图2,在等腰直角△ABC中,∠ACB=90°,AC=BC,过点C作直线CE,AD⊥CE于D,BE⊥CE于E,AD=2.5cm,DE=1.7cm,求BE的长;
(3)拓展延伸:如图3,在平面直角坐标系中,A(﹣1,0),C(1,3),△ABC为等腰直角三角形,∠ACB=90°,AC=BC,求B点坐标.
【答案】(1)证明见解析;
(2)0.8cm;
(3)(4,1).
【解答】(1)证明:∵AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∵∠ACB=90°,
∴∠ACD+∠ECB=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
(2)解:∵BE⊥CE,AD⊥CE,
∴∠ADC=∠CEB=90°,
∴∠CBE+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACD=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴AD=CE=2.5cm,CD=BE,
∴BE=CD=CE﹣DE=2.5﹣1.7=0.8(cm),
即BE的长为0.8cm;
(3)解:如图3,过点C作直线l∥x轴,交y轴于点G,过A作AE⊥l于点E,过B作BF⊥l于点F,交x轴于点H,
则∠AEC=∠CFB=∠ACB=90°,
∵A(﹣1,0),C(1,3),
∴EG=OA=1,CG=1,FH=AE=OG=3,
∴CE=EG+CG=2,
∵∠ACE+∠EAC=90°,∠ACE+∠FCB=90°,
∴∠EAC=∠FCB,
在△AEC和△CFB中,
,
∴△AEC≌△CFB(AAS),
∴AE=CF=3,BF=CE=2,
∴FG=CG+CF=1+3=4,BH=FH﹣BF=3﹣2=1,
∴B点坐标为(4,1).
【典例2】(1)猜想:如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.试猜想DE、BD、CE有怎样的数量关系,请直接写出;
(2)探究:如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α(其中α为任意锐角或钝角)如果成立,请你给出证明;若不成立,请说明理由;
(3)解决问题:如图3,F是角平分线上的一点,且△ABF和△ACF均为等边三角形,D、E分别是直线m上A点左右两侧的动点,D、E、A互不重合,在运动过程中线段DE的长度始终为n,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并说明理由.
【解答】解:(1)DE=BD+CE,
理由如下:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°,
∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,
∴DE=AD+AE=BD+CE;
(2)结论DE=BD+CE成立,
理由如下:∵∠BAD+∠CAE=180°﹣∠BAC,∠BAD+∠ABD=180°﹣∠ADB,∠ADB=∠BAC,
∴∠ABD=∠CAE,
在△BAD和△ACE中,
,
∴△BAD≌△ACE(AAS),
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE;
(3)△DFE为等边三角形,
理由如下:由(2)得,△BAD≌△ACE,
∴BD=AE,∠ABD=∠CAE,
∴∠ABD+∠FBA=∠CAE+FAC,即∠FBD=∠FAE,
在△FBD和△FAE中,
,
∴△FBD≌△FAE(SAS),
∴FD=FE,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DFE为等边三角形.
【变式2-1】(2022秋 汕尾期中)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
【答案】见试题解答内容
【解答】证明:(1)∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∵DC+CE=DE,
∴AD+BE=DE.
(2)DE=AD﹣BE,
理由:∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC﹣CD=AD﹣BE.
【变式2-2】(2022秋 东台市月考)【一线三等角模型】如图1:点A、B、C在一条直线上,∠A=∠DBE=∠C,当BD=BE时,有△ABD≌△CEB.理由:
∵∠A=∠DBE,∴∠D+∠DBA=180°﹣∠A,∠DBA+∠CBE=180°﹣∠DBE,∴∠D=∠CBE﹣﹣﹣﹣﹣﹣﹣﹣请将全等证明过程补充完整.
【模型运用】如图2:∠ABC=∠CAD=90°,AB=4,AC=AD,求△BAD的面积;
【能力提升】如图3:在等边△DEF中,A,C分别为DE、DF边上的动点,AE=2CD,连接AC,以AC为边在△DEF内作等边△ABC,连接BF,当点A从点E向点D运动(不与点D重合)时,∠CFB的度数变化吗?如不变请求出它的度数,如变化,请说明它是怎样变化的?
【答案】【一线三等角模型】证明见解析部分;
【模型运用】8;
【能力提升】∠CFB=30°.
【解答】【一线三等角模型】证明:如图1:∵∠A=∠DBE,
∴∠D+∠DBA=180°﹣∠A,∠DBA+∠CBE=180°﹣∠DBE,
∴∠D=∠CBE,
在△ABD和△CEB中,
,
∴△ABD≌△CEB(AAS);
【模型运用】解:如图2:过点D作DT⊥BA交BA的延长线于点T.
同法可证△ATD≌△CBA(AAS),
∴DT=AB=4,
∴S△ABD=×AB×DT=×4×4=8;
【能力提升】解:∠CFB=30°不变.
理由:如图3中,在CF上取一点N,使得FN=DC.
∵△ABC,△DEF都是等边三角形,
∴∠D=∠ACB=60°,DA=DF,CA=CB,
∵AE=2CD,CD=FN,
∴DA=CN,
∵∠ACN=∠ACB+∠BCN=∠D+∠CAD,
∴∠BCN=∠DAC,
在△ADC和△CNB中,
,
∴△ADC≌△CNB(SAS),
∴BN=CD,∠D=∠BNC=60°,
∵NF=CD,
∴NB=NF,
∴∠NBF=∠NFB,
∵∠BNC=∠NBF+∠NFB=60°,
∴∠NFB=∠NBF=30°,
∴∠CFB=30°.
【模型二:手拉手模型】
应用:①利用手拉手模型证明三角形全等,便于解决对应的几何问题;
②作辅助线构造手拉手模型,难度比较大。
【类型一:等边三角形中的手拉手模型】
【典例3】阅读与理解:如图1,等边△BDE按如图所示方式设置.
操作与证明:
(1)操作:固定等边△ABC,将△BDE绕点B按逆时针方向旋转120°,连接AD,CE,如图2;在图2中,请直接写出线段CE与AD之间具有怎样的大小关系.
(2)操作:若将图1中的△BDE,绕点B按逆时针方向旋转任意一个角度α(60°<α<180°),连接AD,CE,AD与CE相交于点M,连BM,如图3;在图3中线段CE与AD之间具有怎样的大小关系?∠EMD的度数是多少?证明你的结论.
猜想与发现:
(3)根据上面的操作过程,请你猜想在旋转过程中,∠DMB的度数大小是否会随着变化而变化?请证明你的结论.
【解答】解:(1)EC=AD;
∵将△BDE绕点B按逆时针方向旋转120°,
∴∠ABD=∠CBE,
在△EBC和△DBA中,
,
∴△EBC≌△DBA(SAS),
∴EC=AD;
(2)EC=AD,∠EMD=60°,理由如下:
设AD与BE交于点O,
∵将△BDE绕点B按逆时针方向旋转α度,
∴∠EBC=∠DBA=α,
∵△ABC与△BDE是等边三角形,
∴BC=AB,BD=BE,
∴△EBC≌△DBA(SAS),
∴EC=AD,∠CEB=∠ADB,
∵∠EOM=∠DOB,
∴∠EMD=∠EBD=60°,
(3)不变,理由如下:
过点B作BH⊥AD于点H,BF⊥EC于点F,
∵△EBC≌△DBA,
∴S△EBC=S△DBA,AD=EC,
∴BH=BF,
∴MB平分∠DMC,
∴∠DMB=,
∴∠DMB的度数大小不变
【变式3-1】如图,△ABC和△DCE都是等边三角形,且B,C,D三点在一条直线上,连接AD,BE相交于点P.
(1)求证:BE=AD.
(2)求∠APB的度数.
【解答】(1)证明:∵△ABC和△DCE都是等边三角形,
∴BC=AC,CE=CD,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
即∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)解:由(1)可得△ACD≌△BCE(SAS),
∴∠DAC=∠EBC.
∵∠ACB=∠DAC+∠ADC=60°,
∴∠EBC+∠ADC=∠APB=60°,
即∠APB=60°.
【变式3-1】(2023春 佛山期末)在等边△ABC中,AB=6,点D是射线CB上一点,连接AD.
(1)如图1,当点D在线段CB上时,在线段AC上取一点E,使得CE=BD,求证:AD=BE;
(2)如图2,当点D在CB延长线上时,将线段AD绕点A逆时针旋转角度θ(0°<θ<180°)得到线段AF,连接BF,CF.
①当AF位于∠BAC内部,且∠DAF恰好被AB平分时,若BD=2,求CF的长度;
②如图3,当θ=120°时,记线段BF与线段AC的交点为G,猜想DC与AG的数量关系,并说明理由.
【答案】(1)证明过程见解答;
(2)①;②证明过程见解答.
【解答】(1)证明:∵△ABC是等边三角形,
∴AB=BC=AC,
∠ABC=∠C=∠BAC=60°,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS),
∴AD=BE;
(2)解:①过点F作FH⊥BC于点H,如图2,
在△ABD和△ABF中,
,
∴△ABD≌△ABF(SAS),
∴BF=BD=2,
∠ABF=∠ABD=180°﹣∠ABC=120°,
∴∠FBH=∠ABF﹣∠ABC=60°,
在Rt△BFH中,
∠BFH=90°﹣∠FBH=30°,
∴BH=BF==1,
HF2=BF2﹣BH2=22﹣12=3,
∵CH=BC﹣BH=6﹣1=5,
∴CF2=CH2+HF2=52+3=28,
∴;
②证明:延长AC到点M,使CM等于BD,连接FM,如图3,
∵∠DAF=θ=120°,∠BAC=60°,
∴∠DAB+∠MAF=120°﹣60°=60°,
∵∠ADB+∠DAB=∠ABC=60°,
∴∠ADB=∠MAF,
又∵BC=AC,BD=CM,
∴BC+BD=AC+CM,
即:DC=AM,
在△ADC和△FAM中,
,
∴△ADC≌△FAM(SAS),
∴AC=MF,∠M=∠ACB=60°,
∴MF=AB,∠M=∠BAC,
在△ABG和△MFG中,
,
∴△ABG≌△MFG(AAS),
∴AG=MG,
∴AM=AG+MG=2AG,
∴CD=2AG.
【类型二:等腰三角形的手拉手模型】
【典例4】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上时,∠BAC=90°,
①求证:BD=CE;
②∠BCE= ;
(2)设∠BCE=a,∠BAC=β,
①如图2,当点D在线段BC上移动,求证α+β=180°;
②当点D在射线BC的反向延长线上移动,则a、β之间有怎样的数量关系?请直接写出你的结论.
【解答】(1)①证明:∵AB=AC,AD=AE,∠BAD+∠DAC=∠DAC+∠CAE=90°,
∴∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
②由①知△ABD≌△ACE,
∴∠B=∠ACE,
∴∠BCE=∠ACB+∠ACE=∠ACB+∠B,
又∵∠BAC=90°,
∴∠BCE=90°,
故答案为:90°;
(2)①证明:∵AB=AC,AD=AE,∠BAD+∠DAC=∠DAC+∠CAE,
∴∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE,
∴∠B+∠ACB=α,
∵∠BAC+∠B+∠ACB=180°,
∴α+β=180°;
②α=β.理由如下:如图,由①同理得,△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∴∠BAC+∠ACB=∠ACB+∠BCE,
∴∠BAC=∠BCE,
即α=β.
【变式4-1】如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N.
证明:(1)BD=CE;(2)BD⊥CE.
【解答】证明:(1)∵∠BAC=∠DAE=90°
∴∠BAC+∠CAD=∠DAE+∠CAD
即∠CAE=∠BAD
在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴BD=CE
(2)∵△ABD≌△ACE
∴∠ABN=∠ACE
∵∠ANB=∠CND
∴∠ABN+∠ANB=∠CND+∠NCE=90°
∴∠CMN=90°
即BD⊥CE.
【变式4-2】如图,在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点,连接AD,以AD为直角边作等腰直角三角形ADF.
(1)如图1,若当点D在线段BC上时(不与点B、C重合),证明:△ACF≌△ABD;
(2)如图2,当点D在线段BC的延长线上时,试猜想CF与BD的数量关系和位置关系,并说明理由.
【解答】(1)证明:∵∠BAC=90°,△ADF是等腰直角三角形,
∴∠CAF+∠CAD=90°,∠BAD+∠ACD=90°,
∴∠CAF=∠BAD,
在△ACF和△ABD中,
,
∴△ACF≌△ABD(SAS),
(2)解:CF=BD,CF⊥BD.
理由:∵∠CAB=∠DAF=90°,
∴∠CAB+∠CAD=∠DAF+∠CAD,
即∠CAF=∠BAD,
在△ACF和△ABD中,
,
∴△ACF≌△ABD(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠BCF=∠ACF+∠ACB=45°+45°=90°,
∴CF⊥BD
【变式4-3】(2022秋 惠民县校级期末)(1)如图1,△ABC与△ADE均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:BD=CE;
(2)如图2,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
填空:∠AEB的度数为 60° ;线段BE与AD之间的数量关系是 BE=AD .
(3)拓展探究
如图3,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
【答案】见试题解答内容
【解答】(1)证明:∵∠BAC=∠DAE=40°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△BAD和△CAE中,
∴△BAD≌△CAE,
∴BD=CE.
(2)解:∵△ACB和△DCE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∠CDE=∠CED=60°,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
∴△ACD≌△BCE,
∴BE=AD,∠ADC=∠BEC,
∵点A,D,E在同一直线上,
∴∠ADC=180°﹣60°=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC﹣∠CED=120°﹣60°=60°,
综上,可得
∠AEB的度数为60°;线段BE与AD之间的数量关系是:BE=AD.
故答案为:60°、BE=AD.
(3)解:∵△ACB和△DCE均为等腰直角三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE,
∴BE=AD,∠BEC=∠ADC,
∵点A,D,E在同一直线上,
∴∠ADC=180﹣45=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC﹣∠CED=135﹣45=90°;
∵∠DCE=90°,CD=CE,CM⊥DE,
∴CM=DM=EM,
∴DE=DM+EM=2CM,
∴AE=AD+DE=BE+2CM.
【模型二:直角三角形中的手拉手模型】
【典例5】△ABC与△BDE均为等腰直角三角形,∠ABC=∠DBE=90°.
(1)如图1,当D,B,C在同一直线时,CE的延长线与AD交于点F.求证:∠CFA=90°;
(2)当△ABC与△BDE的位置如图2时,CE的延长线与AD交于点F,猜想∠CFA的大小并证明你的结论;
(3)如图3,当A,E,D在同一直线时(A,D在点E的异侧),CE与AB交于点G,∠BAD=∠ACE,求证:BG+AB=AC.
【解答】(1)证明:∵△ABC和△DBE是等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
在△ABD和△CBE中,
,
∴△ABD≌△CBE(SAS),
∴∠BAD=∠BCE,
∵∠BAD+∠AFE+∠FEA=∠BCE+∠ABC+∠BEC=180°,
又∵∠FEA=∠BEC,
∴∠CFA=∠ABC=90°.
(2)解:∠CFA=90°.
理由如下:
同理可证△ABD≌△CBE(SAS),
∴∠BAD=∠BCE,
∴∠CFA=∠ABC=90°.
(3)过点G作GH⊥AC于点H,同(2)可知∠BAD=∠BCE,
∵∠BAD=∠ACE,
∴∠ACE=∠BCE,
∵AB⊥BC,GH⊥AC,
∴BG=GH,
∵∠BAC=45°,
∴∠BAC=∠AGH=45°,
∴GH=AH,
∴AH=BG,
在Rt△BCG和Rt△HCG中,
,
∴Rt△BCG≌Rt△HCG(HL),
∴BC=CH,
∴AC=AH+CH=BG+BC=BG+AB.
【变式5】如图:已知△ABC中,∠BAC=90°,AB=AC,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作△ADE,使∠DAE=90°,AD=AE,连接CE.
发现问题:
如图1,当点D在边BC上时,
(1)请写出BD和CE之间的位置关系为 BD⊥CE ,并猜想BC和CE、CD之间的数量关系: .
(2)如图2,当点D在边BC的延长线上且其他条件不变时,(1)中BD和CE之间的位置关系;BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
【解答】解:(1)∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ACE=∠ABD=45°,
∴∠BCE=∠ACB+∠ACE=45°+45°=90°,BC=CD+BD=CD+CE,
∴BD⊥CE,
故答案为:BD⊥CE;BC=CD+CE;
(2)BD⊥CE成立,数量关系不成立,关系为BC=CE﹣CD.
理由如下:如图2,∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ACE=∠ABC,
∴BD=BC+CD,∠ACE+∠ACB=90°,
∴BD⊥CE;BC=CE﹣CD
【模型三:作辅助线构造手拉手模型】
【典例6】在△ABC中,AB=AC,∠ABC=α,点D是直线BC上一点,点C关于射线AD的对称点为点E.作直线BE交射线AD于点F.连接CF.
(1)如图1,点D在线段BC上,补全图形,求∠AFB的大小(用含α的代数式表示);
(2)如果∠α=60°,
①如图2,当点D在线段BC上时,用等式表示线段AF,BF,CF之间的数量关系,并证明;
②如图3,当点D在线段CB的延长线上时,直接写出线段AF、BF、CF之间的数量关系.
【解答】解:(1)补全图形如下,
连接AE,
∵点E为点C关于AD的对称点,
∴AE=AC,EF=FC,∠EAD=∠CAD,
设∠EAD=∠CAD=x,
∴∠CAE=2x,
∵AB=AC,
∴∠ACB=∠ABCα.
∴∠BAE=180°﹣2x﹣2α,
∴∠ABE+∠AEB=2x+2α,
∵AE=AB,
∴∠ABE=∠AEB=x+α,
∴∠AFB=∠AEB﹣∠EAD=α;
(2)①AF=BF+CF.
延长FB至点G,使FG=FA,连接AG,
∵AB=AC,
∴∠ABC=α=60°,
∴△ABC为等边三角形,∠BAC=60°,
由(1)知∠AFB=α=60°,
∴△AFG为等边三角形,
∴AG=AF,∠GAF=60°,
∴∠GAB=∠FAC,
在△ABG和△ACF中,
,
∴△ABG≌△ACF(SAS),
∴BG=CF,
∴CF+BF=BG+BF=GF,
∵GF=AF,
∴AF=BF+CF;
②结论为:CF=AF+BF.连接AE.
∵点E为点C关于AD的对称点,
∴AE=AC,EF=FC,∠EAD=∠CAD,
设∠EAD=∠CAD=x,
∴∠CAE=2x,
∵AB=AC=AE,
∴∠ACB=∠ABC=∠BAC=60°.
∴∠DAB=x﹣60°,
∴∠EAB=x+x﹣60°=2x﹣60°,
∵AE=AB,
∴∠ABE=∠AEB==120°﹣x,
∴∠AFE=∠DAB+∠ABE=x﹣60°+120°﹣x=60°,
在BE上取点G,使得FG=FA,连接AG,
∴△AFG为等边三角形,
∴AG=AF,∠GAF=60°,
∴∠GAE=∠FAB=x﹣60°,
在△AGE与△AFB中,
,
∴△AGE≌△AFB(SAS),
∴BF=EG,
∴EF=EG+FG=BF+AF,
∴CF=EF=BF+AF.
【变式6-1】(2022秋 西湖区校级期末)已知,∠MON=90°,点A在边OM上,点P是边ON上一动点,∠OAP=α.以线段AP为边在AP上方作等边△ABP,连接OB、BP,再以线段OB为边作等边△OBC(点C、P在OB的同侧),作CH⊥ON于点H.
(1)如图1,α=60°.①依题意补全图形;②求∠BPH的度数;
(2)如图2,当点P在射线ON上运动时,用等式表示线段OA与CH之间的数量关系,并证明.
【答案】(1)①见解析;②90°;(2)OA=2CH.
【解答】解:(1)①如图所示,即为所求;
②∵△ABP是等边三角形,
∴∠BPA=60°,
∵∠OAP=α=60°,
∴∠OPA=30°,
∴∠BPH=180°﹣∠OPA﹣∠BPA=90°;
(2)OA=2CH,证明如下:
如图,连接BC,PC,
由(2)可知,△ABP是等边三角形,
∴BA=BP,∠ABP=∠BPA=60°,
∵△BOC是等边三角形,
∴BO=BC,∠BOC=60°,
∴∠ABO=60°﹣∠OBP=∠PBC,
∴△ABO≌△PBC(SAS),
∴AO=PC,∠BPC=∠BAO,
∵∠OAP=α,
∴∠BAO=∠BAP+∠OAP=60°+α,
∴∠BPC=60°+α,
∵∠BPN=180°﹣∠APO﹣∠BPA=120°﹣(90°﹣α)=30°+α,
∴∠HPC=∠BPC﹣∠BPN=30°,
∵CH⊥ON,
∴∠CHO=90°,
在Rt△CHP中,PC=2CH,
∴OA=2CH
【模型三:半角模型】等角=要三角形中得半角模型
【典例7】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.已知,△ABC中,AB=AC,∠BAC=α,点D、E在边BC上,且.
(1)如图a,当α=60°时,将△AEC绕点A顺时针旋转60°到△AFB的位置,连结DF.
①∠DAF= ;②求证:DF=DE;
(2)如图b,当α=90°时,猜想BD、DE、CE的数量关系,并说明理由.
【解答】(1)①解:由旋转知,AF=AE,∠BAF=∠CAE,∠EAF=60°,
∵∠DAE=α,∠BAC=α=60°,
∴∠DAE=×60°=30°,
∴∠CAE+∠BAD=∠BAC﹣∠DAE=30°,
∴∠DAF=∠BAD+∠BAF=∠BAD+∠CAE=30°,
故答案为:30°;
②证明:由①知,AF=AE,∠DAF=∠DAE=30°,
∵AB=AC,
∴△DAF≌△DAE(SAS),
∴DF=DE;
(2)解:DE2=BD2+CE2,理由如下:
如图,
将△AEC绕点A顺时针旋转90°到△AFB的位置,连结DF,
∴AF=AE,∠EAF=90°=∠BAC,
∴∠BAF=∠CAE,
∴△BAF≌△CAE(SAS),
∴BF=CE,∠ABF=∠ACE,
在Rt△ABC中,∠C=∠ABC=45°,
∴∠ABF=45°,
∴∠DBF=90°,根据勾股定理得,DF2=BD2+BF2,
∴DF2=BD2+CE2,
同(1)②的方法得,DF=DE,
∴DE2=BD2+CE2.
【变式7】已知∠MBN=60°,等边△BEF与∠MBN顶点B重合,将等边△BEF绕顶点B顺时针旋转,边EF所在直线与∠MBN的BN边相交于点C,并在BM边上截取AB=BC,连接AE.
(1)将等边△BEF旋转至如图①所示位置时,求证:CE=BE+AE;
(2)将等边△BEF顺时针旋转至如图②、图③位置时,请分别直接写出AE,BE,CE之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若BF=4,AE=1,则CE= 3或5 .
【解答】(1)证明:∵△BEF为等边三角形,
∴BE=EF=BF,∠EBF=60°,
∴∠EBA+∠ABF=60°,
∵∠MBN=60°,
∴∠CBF+∠ABF=60°,
∴∠EBA=∠CBF,
在△ABE与△CBF中,
,
∴△ABE≌△CBF(SAS),
∴AE=CF,
∵CE=EF+CF,
∴CE=BE+AE;
(2)解:图②结论为CE=BE﹣AE,图③结论为CE=AE﹣BE,
图②的理由如下:
∵△BEF为等边三角形,
∴BE=EF=BF,∠EBF=60°,
∴∠EBA+∠ABF=60°,
∵∠MBN=60°,
∴∠CBF+∠ABF=60°,
∴∠EBA=∠CBF,
在△ABE与△CBF中,
,
∴△ABE≌△CBF(SAS),
∴AE=CF,
∵CE=EF﹣CF,
∴CE=BE﹣AE,
图③的利用如下:
∵△BEF为等边三角形,
∴BE=EF=BF,∠EBF=60°,
∴∠EBA+∠ABF=60°,
∵∠MBN=60°,
∴∠CBF+∠ABF=60°,
∴∠EBA=∠CBF,
在△ABE与△CBF中,
,
∴△ABE≌△CBF(SAS),
∴AE=CF,
∵CE=CF﹣EF,
∴CE=AE﹣BE;
(3)解:在(1)条件下,CE=BE+AE=BF+AE=4+1=5;
在(2)条件下,CE=BE﹣AE=BF﹣AE=4﹣1=3,
综上所述,CE=3或5,
故答案为:3或5.
【变式7-2】(2021秋 桦甸市期末)如图,△ABC是等边三角形,D是边BC上一点(点D不与点B,C重合),作∠EDF=60°,使角的两边分别交边AB,AC于点E,F,且BD=CF.
(1)如图①,若DE⊥BC,则∠DFC= 90 度;
(2)如图②,D是边BC上一点(点D不与点B,C重合),求证:BE=CD;
(3)如图③,若D是边BC的中点,且AB=2,则四边形AEDF的周长为 4 .
【答案】(1)90;
(2)证明见解析;
(3)4.
【解答】解:(1)∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵DE⊥BC,即∠BDE=90°,∠EDF=60°,
∴∠BED=∠CDF=30°,
∴∠DFC=90°,
故答案为:90;
(2)∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠EDF+∠CDF=∠B+∠BED,且∠EDF=60°,
∴∠CDF=∠BED,
在△BDE和△CFD中,
,
∴△BDE≌△CFD(AAS),
∴BE=CD;
(3)∵△ABC是等边三角形,AB=2,
∴∠B=∠C=60°,AB=BC=AC=2,
∵D为BC中点,且BD=CF,
∴BD=CD=CF=AF=1,
由(2)知△BDE≌△CFD,
∴BE=CD=1,DE=DF,
∵∠B=60°,
∴△BDE是等边三角形,
∴DE=DF=1,
则四边形AEDF的周长为AE+DE+DF+AF=4,
故答案为:4.
【变式7-3】】等边△ABC,D为△ABC外一点,∠BDC=120°,BD=DC,∠MDN=60°,射线DM与直线AB相交于点M,射线DN与直线AC相交于点N,
①当点M、N在边AB、AC上,且DM=DN时,直接写出BM、NC、MN之间的数量关系.
②当点M、N在边AB、AC上,且DM≠DN时,猜想①中的结论还成立吗?若成立,请证明.
③当点M、N在边AB、CA的延长线上时,请画出图形,并写出BM、NC、MN之间的数量关系.
【解答】解①BM、NC、MN之间的数量关系 BM+NC=MN.
②猜想:结论仍然成立.
证明:在CN的反向延长线上截取CM1=BM,连接DM1.
∵∠MBD=∠M1CD=90°,BD=CD,
∴△DBM≌△DCM1,
∴DM=DM1,∠MBD=∠M1CD,M1C=BM,
∵∠MDN=60°,∠BDC=120°,
∴∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N=M1C+NC=BM+NC,
③证明:在CN上截取CM1=BM,连接DM1.
可证△DBM≌△DCM1,
∴DM=DM1,
可证∠CDN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N,
∴NC﹣BM=MN.
【模型四:对角互补模型】
应用:通过做垂线或者利用旋转构造全等三角形解决问题。
【典例9】(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图(2),在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
【解答】证明:(1)EF2=BE2+CF2,
理由如下:如图(1)延长ED到G,使DG=ED,连接CG,FG,
在△DCG与△DBE中,
,
∴△DCG≌△DBE(SAS),
∴DG=DE,CG=BE,∠B=∠DCG,
又∵DE⊥DF,
∴FD垂直平分线段EG,
∴FG=FE,
∵∠A=90°,
∴∠B+∠ACB=90°,
∴∠FCG=90°,
在△CFG中,CG2+CF2=FG2,
∴EF2=BE2+CF2;
(2)如图(2),结论:EF=EB+FC,
理由如下:延长AB到M,使BM=CF,
∵∠ABD+∠C=180°,又∠ABD+∠MBD=180°,
∴∠MBD=∠C,
在△BDM和△CDF中,
,
∴△BDM≌△CDF(SAS),
∴DM=DF,∠BDM=∠CDF,
∴∠EDM=∠EDB+∠BDM=∠EDB+∠CDF=∠CDB﹣∠EDF=120°﹣60°=60°=∠EDF,
在△DEM和△DEF中,
,
∴△DEM≌△DEF(SAS),
∴EF=EM,
∴EF=EM=BE+BM=EB+CF.
【变式9-1】(九台区期末)【教材呈现】如图是华师版八年级上册数学教材96页的部分内容.
已知:如图13.5.4,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为点D和点E.求证:PD=PE.分析:图中有两个直角三角形PDO和PEO,只要证明这两个三角形全等便可证得PD=PE.
【问题解决】请根据教材分析,结合图①写出证明PD=PE的过程.
【类比探究】
(1)如图②,OC是∠AOB的平分线,P是OC上任意一点,点M,N分别在OB和OA上,连接PM和PN,若∠PMO+∠PNO=180°,求证:PM=PN;
(2)如图③,△ABC的周长是12,BO、CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若OD=3,则△ABC的面积为 18 .
【答案】【问题解决】证明过程见解析.
【类比探究】(1)证明过程见解析.
(2)18.
【解答】【问题解决】证明:在△OPE和△OPD中,
,
∴△OPE≌△OPD(AAS),
∴PD=PE;
【类比探究】(1)证明:如图②,过点P作PE⊥OB于E,PF⊥OA于F,
∵OC是∠AOB的平分线,PE⊥OB,PF⊥OA,
∴PE=PF,
∵∠PMO+∠PME=180°,∠PMO+∠PNO=180°,
∴∠PME=∠PNO,
在△PME和△PNF中,
,
∴△PME≌△PNF(AAS),
∴PM=PN;
(2)解:过O作OE⊥AB与E,OF⊥AC于F,
∵BO、CO分别平分∠ABC和∠ACB,
∴EO=DO,OF=DO,
∵OD=3,
∴EO=FO=3,
∵△ABC的周长是12,
∴AB+BC+AC=12,
∴△ABC的面积:AB EO+AC FO+CB DO=(AB+AC+BC)=×12=18,
故答案为:18.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2023/7/13 12:18:00;用户:gaga;邮箱:18376708956;学号:18
【变式9-2】(1)阅读理解:
如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:
延长AD到点E使DE=AD,再连接BE,这样就把AB,AC,2AD集中在△ABE中,利用三角形三边的关系可判断线段AE的取值范围是 ;则中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,此时:BE+CF EF(填“>”或“=”或“<”);
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180,CB=CD,∠BCD=140°,以C为顶点作∠ECF=70°,边CE,CF分别交AB,AD于E,F两点,连接EF,此时:BE+DF EF(填“>”或“=”或“<“);
(4)若在图③的四边形ABCD中,∠ECF=α(0°<α<90°),∠B+∠D=180,CB=CD,且(3)中的结论仍然成立,则∠BCD= (用含α的代数式表示).
【解答】解:(1)在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴BE=AC=3,
在△ABE中,AB﹣BE<AE<AB+BE,
即2<AE<8,
∴2<2AD<8,
∴1<AD<4,
故答案为:2<AE<8;1<AD<4;
(2)如图,延长FD至点G,使DG=DF,连接BG,EG,
∵点D是BC的中点,
∴DB=DC,
∵∠BDG=∠CDF,DG=DF,
∴△BDG≌△CDF(SAS),
∴BG=CF,
∵ED⊥FD,FD=GD,
∴EF=EG,
在△BEG中,BE+BG>EG,
∴BE+CF>EF,
故答案为:>;
(3)BE+DF=EF,
如图,延长AB至点G,使BG=DF,连接CG,
∵∠ABC+∠D=180°,∠ABC+∠CBG=180°,
∴∠CBG=∠D,
又∵CB=CD,BG=DF,
∴△CBG≌△CDF(SAS),
∴CG=CF,∠BCG=∠DCF,
∵∠BCD=140°,∠ECF=70°,
∴∠DCF+∠BCE=70°,
∴∠BCE+∠BCG=70°,
∴∠ECG=∠ECF=70°,
又∵CE=CE,CG=CF,
∴△ECG≌△ECF(SAS),
∴EG=EF,
∵BE+BG=EG,
∴BE+DF=EF,
故答案为:=;
(4)由(3)同理可得△CBG≌△CDF,
∴CG=CF,∠BCG=∠DCF,
若BE+DF=EF,
则EG=EF,
∴△ECF≌△ECG(SSS),
∴∠ECG=∠ECF,
∴∠BCD=2∠ECF=2α,
故答案为:2α.
【典例10】(1)如图1,四边形ABCD是边长为5 cm的正方形,E,F分别在AD,CD边上,∠EBF=45°.为了求出△DEF的周长.小南同学的探究方法是:
如图2,延长EA到H,使AH=CF,连接BH,先证△ABH≌△CBF,再证△EBH≌△EBF,得EF=EH,从而得到△DEF的周长= cm;
(2)如图3,在四边形ABCD中,AB=AD,∠BAD=100°,∠B=∠ADC=90°.E,F分别是线段BC,CD上的点.且∠EAF=50°.探究图中线段EF,BE,FD之间的数量关系;
(3)如图4,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是线段BC,CD上的点,且2∠EAF=∠BAD,(2)中的结论是否仍然成立,若成立,请证明,若不成立,请说明理由;
(4)若在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别在CB、DC的延长线上,且2∠EAF=∠BAD,请画出图形,并直接写出线段EF、BE、FD之间的数量关系.
【解答】解:(1)如图1,延长EA到H,使AH=CF,连接BH,
∵四边形ABCD是正方形,
∴AB=BC=AD=CD=5cm,∠BAD=∠BCD=90°,
∴∠BAH=∠BCF=90°,
又∵AH=CF,AB=BC,
∴△ABH≌△CBF(SAS),
∴BH=BF,∠ABH=∠CBF,
∵∠EBF=45°,
∴∠CBF+∠ABE=45°=∠HBA+∠ABE=∠EBF,
∴∠EBH=∠EBF,
又∵BH=BF,BE=BE,
∴△EBH≌△EBF(SAS),
∴EF=EH,
∴EF=EH=AE+CF,
∴△DEF的周长=DE+DF+EF=DE+DF+AE+CF=AD+CD=10(cm).
故答案为:10.
(2)EF=BE+DF.
证明:如图2所示,延长FD到点G.使DG=BE.连接AG,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠BAD=100°,∠EAF=50°,
∴∠BAE+∠FAD=∠DAG+∠FAD=50°,
∴∠EAF=∠FAG=50°,
在△EAF和△GAF中,
,
∴△EAF≌△GAF(SAS),
∴EF=FG=DF+DG,
∴EF=BE+DF;
(3)成立.
证明:如图3,延长EB到G,使BG=DF,连接AG.
∵∠ABC+∠D=180°,∠ABG+∠ABC=180°,
∴∠ABG=∠D,
∵在△ABG与△ADF中,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠BAG=∠DAF,
∵2∠EAF=∠BAD,
∴∠DAF+∠BAE=∠BAG+∠BAE=∠BAD=∠EAF,
∴∠GAE=∠EAF,
又AE=AE,
∴△AEG≌△AEF(SAS),
∴EG=EF,
∵EG=BE+BG,
∴EF=BE+FD;
(4)EF=DF﹣BE,
理由如下:在DF上截取DH,使DH=BE,
∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,
∴∠ABE=∠ADH,且AB=AD,DH=BE,
∴△ABE≌△ADH(SAS),
∴∠BAE=∠DAH,AH=AE,
∵∠EAF=∠BAD,
∴∠DAH+∠BAF=∠BAD,
∴∠HAF=∠BAD=∠EAF,且AF=AF,AE=AH,
∴△FAH≌△FAE(SAS),
∴HF=EF,
∴EF=HF=DF﹣DH=DF﹣BE
【变式10-1】如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,求证:EF=BE+FD.
【解答】证明:延长CB至M,使BM=FD,连接AM,如图所示:
∵∠ABC+∠D=180°,∠ABM+∠ABC=180°,
∴∠ABM=∠D,
在△ABM与△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AF=AM,∠BAM=∠DAF,
∵∠EAF=∠BAD,
∴∠DAF+∠BAE=∠BAD=∠FAE,
∴∠BAM+∠BAE=∠EAF,
即∠MAE=∠EAF,
在△AME与△AFE中,
,
∴△AME≌△AFE(SAS),
∴EF=ME,
∵ME=BE+BM,
∴EF=BE+FD.
【变式10-2】“截长补短法”证明线段的和差问题:
先阅读背景材料,猜想结论并填空,然后做问题探究.
背景材料:
(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.探究的方法是,延长FD到点G.使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出的结论是 .
探索问题:
(2)如图2,若四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立?成立的话,请写出推理过程.
【解答】证明:(1)在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为:EF=BE+DF.
(2)解:结论EF=BE+DF仍然成立;
理由:延长FD到点G.使DG=BE.连接AG,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF.
【模型五:平行+线段中点构造全等模型】
【结论】如图,AB∥CD,点E、F分别在直线AB、CD上,点O为EF中点,则△POE≌△QOF
口诀:有中点,有平行,轻轻延长就能行
【典例11】已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图③.写出AF、EF与AB的数量关系,并对图②进行证明.
【解答】(1)证明:如图①,延长AD、EF交于点G,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠G=∠BAD,
∴∠G=∠CAD,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(AAS),
∴AB=GE,
∵GE=FG+EF=AF+EF,
∴AF+EF=AB;
(2)结论:AF﹣EF=AB.
证明:如图②,延长AD、EF交于点G,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠G=∠BAD,
∴∠G=∠CAD,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(AAS),
∴AB=GE,
∵GE=FG﹣EF=AF﹣EF,
∴AF﹣EF=AB;
(3)结论:EF﹣AF=AB.
证明:如图③,延长AD交EF于点G,
∵AD平分∠PAC,
∴∠PAD=∠CAD,
∵EF∥AB,
∴∠AGF=∠PAD,
∴∠AGF=∠CAD,∠ABD=∠GED,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(ASA),
∴AB=GE,
∵EF﹣FG=GE,
∴EF﹣AF=AB;
【变式11-1】如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA⊥OC.
(1)求证:CO平分∠ACD;
(2)求证:AB+CD=AC.
【解答】解:
(1)如图,延长AO交CD的延长线于点E,
∵O为BD的中点,
∴BO=DO,
在△AOB与△EOD中,
∴△AOB≌△EOD,(ASA)
∴AO=AE,
又∵OA⊥OC,
∴AC=CE
∴CO平分∠ACD;(三线合一)
(2)由△AOB≌△EOD
可得AB=DE
∴AB+CD=CD+DE=CE
∵AC=CE
∴AB+CD=AC
【变式11-2】如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,求证AD和BC的关系。
【解答】解:如图,延长AE交BC于F.
∵AB⊥BC,AB⊥AD,
∴AD∥BC
∴∠D=∠C,∠DAE=∠CFE,
又∵点E是CD的中点,
∴DE=CE.
∵在△AED与△FEC中,
,
∴△AED≌△FEC(AAS),
∴AE=FE,AD=FC.
∵AD=5,BC=10.
∴BF=5
∴AD=
19.(2023春 青秀区校级期末)已知平行四边形ABCD,E为BC边上的中点.
(1)如图1,若BC=2CD,求证:DE平分∠ADC;
(2)若F为AB边上一点,连结DF,EF;
①如图2,若S△EFB=1,S△CDE=4,求S△DEF;
②如图3,若∠EFB+∠CDE=90°,请你写出线段AF,BF,DF之间的数量关系,并证明.
【答案】(1)见解析;
(2)①S△DEF=5;
②DF=AF+2BF,证明见解析.
【解答】(1)证明:∵E为BC的中点,
∴BC=2BE=2CE,
∵BC=2CD,
∴CD=CD,
∴∠CDE=∠CED,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠ADE=∠CED,
∴∠ADE=∠CDE,
∴DE平分∠ADC;
(2)①解:延长FE,交DC延长线于点G,如图,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠FBE=∠GCE,∠BFE=∠CGE,
∵E为BC的中点,
∴BE=CE,
在△BEF和△CEG中,
,
∴△BEF≌△CEG(AAS),
∴EF=EG,S△BEF=S△CEG,
∵S△EFB=1,S△CDE=4,
∴S△CEG=1,
S△DEG=S△CDE+S△CEG=4+1=5,
∵EF=EG,
∴S△DEF=S△DEG=5;
②DF=AF+2BF,证明如下:
延长FE,交DC延长线于点G,如图,
由①可知,△BEF≌△CEG,
∴EF=EG,BF=CG,∠EFB=∠EGC,
∵∠EFB+∠CDE=90°,
∴∠EGD+∠GDE=90°,即DE⊥FG,
∴△DFG为等腰三角形,DF=DG,
∴DF=DG=CD+CG=AB+BF=AF+BF+BF=AF+2BF,
即DF=AF+2BF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题05 全等三角形重难点模型(五大模型)
重难点题型归纳
【模型一:一线三等角型】
【模型二:手拉手模型】
【模型三:半角模型】
【模型四:对角互补模型】
【模型五:平行+线段中点构造全等模型】
【模型一:一线三等角型】
如图一,∠D=∠BCA=∠E=90°,BC=AC。 结论:Rt△BDC≌Rt△CEA
模型二 一线三等角全等模型
如图二,∠D=∠BCA=∠E,BC=AC。 结论:△BEC≌△CDA
图一 图二
应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;
②与函数综合应用中有利于点的坐标的求解。
【典例1】如图,平面直角坐标系中有点A(﹣1,0)和y轴上一动点B(0,a),其中a>0,以B点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).
(1)当a=2时,则C点的坐标为 ;
(2)动点B在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.
【变式1-1】如图,在△PMN中,PM=PN,PM⊥PN,P(0,2),N(2,﹣2),则M的坐标是( )
A.(﹣2,0) B.(﹣2,0) C.(﹣2,0) D.(﹣4,0)
【变式1-2】在学习完“探索全等三角形全等的条件”一节后,一同学总结出很多全等三角形的模型,他设计了以下问题给同桌解决:如图,做一个“U”字形框架PABQ,其中AB=42cm,AP,BQ足够长,PA⊥AB于点A,点M从B出发向A运动,同时点N从B出发向Q运动,点M,N运动的速度之比为3:4,当两点运动到某一瞬间同时停止,此时在射线AP上取点C,使△ACM与△BMN全等,则线段AC的长为 cm.
【变式1-3】阅读理解,自主探究:
“一线三垂直”模型是“一线三等角”模型的特殊情况,即三个等角角度为90°,于是有三组边相互垂直.所以称为“一线三垂直模型”.当模型中有一组对应边长相等时,则模型中必定存在全等三角形.
(1)问题解决:如图1,在等腰直角△ABC中,∠ACB=90°,AC=BC,过点C作直线DE,AD⊥DE于D,BE⊥DE于E,求证:△ADC≌△CEB;
(2)问题探究:如图2,在等腰直角△ABC中,∠ACB=90°,AC=BC,过点C作直线CE,AD⊥CE于D,BE⊥CE于E,AD=2.5cm,DE=1.7cm,求BE的长;
(3)拓展延伸:如图3,在平面直角坐标系中,A(﹣1,0),C(1,3),△ABC为等腰直角三角形,∠ACB=90°,AC=BC,求B点坐标.
【典例2】(1)猜想:如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.试猜想DE、BD、CE有怎样的数量关系,请直接写出;
(2)探究:如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α(其中α为任意锐角或钝角)如果成立,请你给出证明;若不成立,请说明理由;
(3)解决问题:如图3,F是角平分线上的一点,且△ABF和△ACF均为等边三角形,D、E分别是直线m上A点左右两侧的动点,D、E、A互不重合,在运动过程中线段DE的长度始终为n,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并说明理由.
【变式2-1】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
【变式2-2】【一线三等角模型】如图1:点A、B、C在一条直线上,∠A=∠DBE=∠C,当BD=BE时,有△ABD≌△CEB.理由:
∵∠A=∠DBE,∴∠D+∠DBA=180°﹣∠A,∠DBA+∠CBE=180°﹣∠DBE,
∴∠D=∠CBE﹣﹣﹣﹣﹣﹣﹣﹣请将全等证明过程补充完整.
【模型运用】如图2:∠ABC=∠CAD=90°,AB=4,AC=AD,求△BAD的面积;
【能力提升】如图3:在等边△DEF中,A,C分别为DE、DF边上的动点,AE=2CD,连接AC,以AC为边在△DEF内作等边△ABC,连接BF,当点A从点E向点D运动(不与点D重合)时,∠CFB的度数变化吗?如不变请求出它的度数,如变化,请说明它是怎样变化的?
【模型二:手拉手模型】
应用:①利用手拉手模型证明三角形全等,便于解决对应的几何问题;
②作辅助线构造手拉手模型,难度比较大。
【类型一:等边三角形中的手拉手模型】
【典例3】阅读与理解:如图1,等边△BDE按如图所示方式设置.
操作与证明:
(1)操作:固定等边△ABC,将△BDE绕点B按逆时针方向旋转120°,连接AD,CE,如图2;在图2中,请直接写出线段CE与AD之间具有怎样的大小关系.
(2)操作:若将图1中的△BDE,绕点B按逆时针方向旋转任意一个角度α(60°<α<180°),连接AD,CE,AD与CE相交于点M,连BM,如图3;在图3中线段CE与AD之间具有怎样的大小关系?∠EMD的度数是多少?证明你的结论.
猜想与发现:
(3)根据上面的操作过程,请你猜想在旋转过程中,∠DMB的度数大小是否会随着变化而变化?请证明你的结论.
【变式3-1】如图,△ABC和△DCE都是等边三角形,且B,C,D三点在一条直线上,连接AD,BE相交于点P.(1)求证:BE=AD. (2)求∠APB的度数.
【变式3-1】在等边△ABC中,AB=6,点D是射线CB上一点,连接AD.
(1)如图1,当点D在线段CB上时,在线段AC上取一点E,使得CE=BD,求证:AD=BE;
(2)如图2,当点D在CB延长线上时,将线段AD绕点A逆时针旋转角度θ(0°<θ<180°)得到线段AF,连接BF,CF.
①当AF位于∠BAC内部,且∠DAF恰好被AB平分时,若BD=2,求CF的长度;
②如图3,当θ=120°时,记线段BF与线段AC的交点为G,猜想DC与AG的数量关系,并说明理由.
【类型二:等腰三角形的手拉手模型】
【典例4】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上时,∠BAC=90°,
①求证:BD=CE;
②∠BCE= ;
(2)设∠BCE=a,∠BAC=β,
①如图2,当点D在线段BC上移动,求证α+β=180°;
②当点D在射线BC的反向延长线上移动,则a、β之间有怎样的数量关系?请直接写出你的结论.
【变式4-1】如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N.
证明:(1)BD=CE;(2)BD⊥CE.
【变式4-2】如图,在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点,连接AD,以AD为直角边作等腰直角三角形ADF.
(1)如图1,若当点D在线段BC上时(不与点B、C重合),证明:△ACF≌△ABD;
(2)如图2,当点D在线段BC的延长线上时,试猜想CF与BD的数量关系和位置关系,并说明理由.
【变式4-3】(1)如图1,△ABC与△ADE均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:BD=CE;
(2)如图2,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
填空:∠AEB的度数为 ;线段BE与AD之间的数量关系是 .
(3)拓展探究
如图3,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
【模型二:直角三角形中的手拉手模型】
【典例5】△ABC与△BDE均为等腰直角三角形,∠ABC=∠DBE=90°.
(1)如图1,当D,B,C在同一直线时,CE的延长线与AD交于点F.求证:∠CFA=90°;
(2)当△ABC与△BDE的位置如图2时,CE的延长线与AD交于点F,猜想∠CFA的大小并证明你的结论;
(3)如图3,当A,E,D在同一直线时(A,D在点E的异侧),CE与AB交于点G,∠BAD=∠ACE,求证:BG+AB=AC.
【变式5】如图:已知△ABC中,∠BAC=90°,AB=AC,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作△ADE,使∠DAE=90°,AD=AE,连接CE.
发现问题:
如图1,当点D在边BC上时,
(1)请写出BD和CE之间的位置关系为 ,并猜想BC和CE、CD之间的数量关系: .
(2)如图2,当点D在边BC的延长线上且其他条件不变时,(1)中BD和CE之间的位置关系;BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
【模型三:作辅助线构造手拉手模型】
【典例6】在△ABC中,AB=AC,∠ABC=α,点D是直线BC上一点,点C关于射线AD的对称点为点E.作直线BE交射线AD于点F.连接CF.
(1)如图1,点D在线段BC上,补全图形,求∠AFB的大小(用含α的代数式表示);
(2)如果∠α=60°,
①如图2,当点D在线段BC上时,用等式表示线段AF,BF,CF之间的数量关系,并证明;
②如图3,当点D在线段CB的延长线上时,直接写出线段AF、BF、CF之间的数量关系.
【变式6-1】已知,∠MON=90°,点A在边OM上,点P是边ON上一动点,∠OAP=α.以线段AP为边在AP上方作等边△ABP,连接OB、BP,再以线段OB为边作等边△OBC(点C、P在OB的同侧),作CH⊥ON于点H.
(1)如图1,α=60°.①依题意补全图形;②求∠BPH的度数;
(2)如图2,当点P在射线ON上运动时,用等式表示线段OA与CH之间的数量关系,并证明.
【模型三:半角模型】等角=要三角形中得半角模型
【典例7】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.已知,△ABC中,AB=AC,∠BAC=α,点D、E在边BC上,且EF=.
(1)如图a,当α=60°时,将△AEC绕点A顺时针旋转60°到△AFB的位置,连结DF.
①∠DAF= ;②求证:DF=DE;
(2)如图b,当α=90°时,猜想BD、DE、CE的数量关系,并说明理由.
【变式7-1】已知∠MBN=60°,等边△BEF与∠MBN顶点B重合,将等边△BEF绕顶点B顺时针旋转,边EF所在直线与∠MBN的BN边相交于点C,并在BM边上截取AB=BC,连接AE.
(1)将等边△BEF旋转至如图①所示位置时,求证:CE=BE+AE;
(2)将等边△BEF顺时针旋转至如图②、图③位置时,请分别直接写出AE,BE,CE之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若BF=4,AE=1,则CE= .
【变式7-2】如图,△ABC是等边三角形,D是边BC上一点(点D不与点B,C重合),作∠EDF=60°,使角的两边分别交边AB,AC于点E,F,且BD=CF.
(1)如图①,若DE⊥BC,则∠DFC= 度;
(2)如图②,D是边BC上一点(点D不与点B,C重合),求证:BE=CD;
(3)如图③,若D是边BC的中点,且AB=2,则四边形AEDF的周长为 .
【变式7-3】】等边△ABC,D为△ABC外一点,∠BDC=120°,BD=DC,∠MDN=60°,射线DM与直线AB相交于点M,射线DN与直线AC相交于点N,
①当点M、N在边AB、AC上,且DM=DN时,直接写出BM、NC、MN之间的数量关系.
②当点M、N在边AB、AC上,且DM≠DN时,猜想①中的结论还成立吗?若成立,请证明.
③当点M、N在边AB、CA的延长线上时,请画出图形,并写出BM、NC、MN之间的数量关系.
【模型四:对角互补模型】
应用:通过做垂线或者利用旋转构造全等三角形解决问题。
【典例9】(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图(2),在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
【变式9-1】【教材呈现】如图是华师版八年级上册数学教材96页的部分内容.
已知:如图13.5.4,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为点D和点E.求证:PD=PE.分析:图中有两个直角三角形PDO和PEO,只要证明这两个三角形全等便可证得PD=PE.
【问题解决】请根据教材分析,结合图①写出证明PD=PE的过程.
【类比探究】
(1)如图②,OC是∠AOB的平分线,P是OC上任意一点,点M,N分别在OB和OA上,连接PM和PN,若∠PMO+∠PNO=180°,求证:PM=PN;
(2)如图③,△ABC的周长是12,BO、CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若OD=3,则△ABC的面积为 .
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2023/7/13 12:18:00;用户:gaga;邮箱:18376708956;学号:18
【变式9-2】(1)阅读理解:
如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:
延长AD到点E使DE=AD,再连接BE,这样就把AB,AC,2AD集中在△ABE中,利用三角形三边的关系可判断线段AE的取值范围是 ;则中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,此时:BE+CF EF(填“>”或“=”或“<”);
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180,CB=CD,∠BCD=140°,以C为顶点作∠ECF=70°,边CE,CF分别交AB,AD于E,F两点,连接EF,此时:BE+DF EF(填“>”或“=”或“<“);
(4)若在图③的四边形ABCD中,∠ECF=α(0°<α<90°),∠B+∠D=180,CB=CD,且(3)中的结论仍然成立,则∠BCD= (用含α的代数式表示).
【典例10】(1)如图1,四边形ABCD是边长为5 cm的正方形,E,F分别在AD,CD边上,∠EBF=45°.为了求出△DEF的周长.小南同学的探究方法是:
如图2,延长EA到H,使AH=CF,连接BH,先证△ABH≌△CBF,再证△EBH≌△EBF,得EF=EH,从而得到△DEF的周长= cm;
(2)如图3,在四边形ABCD中,AB=AD,∠BAD=100°,∠B=∠ADC=90°.E,F分别是线段BC,CD上的点.且∠EAF=50°.探究图中线段EF,BE,FD之间的数量关系;
(3)如图4,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是线段BC,CD上的点,且2∠EAF=∠BAD,(2)中的结论是否仍然成立,若成立,请证明,若不成立,请说明理由;
(4)若在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别在CB、DC的延长线上,且2∠EAF=∠BAD,请画出图形,并直接写出线段EF、BE、FD之间的数量关系.
【变式10-1】如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,求证:EF=BE+FD.
【变式10-2】“截长补短法”证明线段的和差问题:
先阅读背景材料,猜想结论并填空,然后做问题探究.
背景材料:
(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.探究的方法是,延长FD到点G.使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出的结论是 .
探索问题:
(2)如图2,若四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立?成立的话,请写出推理过程.
【模型五:平行+线段中点构造全等模型】
【结论】如图,AB∥CD,点E、F分别在直线AB、CD上,点O为EF中点,则△POE≌△QOF
口诀:有中点,有平行,轻轻延长就能行
【典例11】已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图③.写出AF、EF与AB的数量关系,并对图②进行证明.
【变式11-1】如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA⊥OC.
(1)求证:CO平分∠ACD;
(2)求证:AB+CD=AC.
【变式11-2】如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,求证AD和BC的关系。
【变式11-3】(2023春 青秀区校级期末)已知平行四边形ABCD,E为BC边上的中点.
(1)如图1,若BC=2CD,求证:DE平分∠ADC;
(2)若F为AB边上一点,连结DF,EF;
①如图2,若S△EFB=1,S△CDE=4,求S△DEF;
②如图3,若∠EFB+∠CDE=90°,请你写出线段AF,BF,DF之间的数量关系,并证明.
专题05 全等三角形重难点模型(五大模型)
重难点题型归纳
【模型一:一线三等角型】
【模型二:手拉手模型】
【模型三:半角模型】
【模型四:对角互补模型】
【模型五:平行+线段中点构造全等模型】
【模型一:一线三等角型】
如图一,∠D=∠BCA=∠E=90°,BC=AC。 结论:Rt△BDC≌Rt△CEA
模型二 一线三等角全等模型
如图二,∠D=∠BCA=∠E,BC=AC。 结论:△BEC≌△CDA
图一 图二
应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;
②与函数综合应用中有利于点的坐标的求解。
【典例1】如图,平面直角坐标系中有点A(﹣1,0)和y轴上一动点B(0,a),其中a>0,以B点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).
(1)当a=2时,则C点的坐标为 ;
(2)动点B在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.
【解答】解:(1)如图1中,过点C作CE⊥y轴于E,则∠CEB=∠AOB.
∵△ABC是等腰直角三角形,
∴BC=BA,∠ABC=90°,
∴∠BCE+∠CBE=90°=∠BAO+∠CBE,
∴∠BCE=∠ABO,
在△BCE和△BAO中,
,
∴△CBE≌△BAO(AAS),
∵A(﹣1,0),B(0,2),
∴AO=BE=1,OB=CE=2,
∴OE=1+2=3,
∴C(﹣2,3),
故答案为:(﹣2,3);
(2)动点A在运动的过程中,c+d的值不变.
理由:过点C作CE⊥y轴于E,则∠CEA=∠AOB,
∵△ABC是等腰直角三角形,
∴BC=BA,∠ABC=90°,
∴∠BCE+∠CBE=90°=∠ABO+∠CBE,
∴∠BCE=∠ABO,
在△BCE和△BAO中,
,
∴△CBE≌△BAO(AAS),
∵B(﹣1,0),A(0,a),
∴BO=AE=1,AO=CE=a,
∴OE=1+a,
∴C(﹣a,1+a),
又∵点C的坐标为(c,d),
∴c+d=﹣a+1+a=1,
即c+d的值不变.
【变式1-1】(2021秋 鼓楼区校级期末)如图,在△PMN中,PM=PN,PM⊥PN,P(0,2),N(2,﹣2),则M的坐标是( )
A.(﹣2,0) B.(﹣2,0) C.(﹣2,0) D.(﹣4,0)
【答案】D
【解答】解:过点N作ND⊥y轴于点D,
∵P(0,2),N(2,﹣2),
∴OP=2,OD=2,DN=2,
∴PD=4,
∵PM⊥PN,
∴∠MPN=90°,
∴∠MPO+∠DPN=90°,
又∵∠DPN+∠PND=90°,
∴∠MPO=∠PND,
又∵∠MOP=∠PDN=90°,
∴△MOP≌△PDN(AAS),
∴OM=PD=4,
∴M(﹣4,0),
故选:D.
【变式1-2】(2022春 金牛区校级期中)在学习完“探索全等三角形全等的条件”一节后,一同学总结出很多全等三角形的模型,他设计了以下问题给同桌解决:如图,做一个“U”字形框架PABQ,其中AB=42cm,AP,BQ足够长,PA⊥AB于点A,点M从B出发向A运动,同时点N从B出发向Q运动,点M,N运动的速度之比为3:4,当两点运动到某一瞬间同时停止,此时在射线AP上取点C,使△ACM与△BMN全等,则线段AC的长为 18或28 cm.
【答案】18或28.
【解答】解:设BM=3tcm,则BN=4tcm,因为∠A=∠B=90°,使△ACM与△BMN全等,可分两种情况:
情况一:当BM=AC,BN=AM时,
∵BN=AM,AB=42cm,
∴4t=42﹣3t,
解得:t=6,
∴AC=BM=3t=3×6=18cm;
情况二:当BM=AM,BN=AC时,
∵BM=AM,AB=42cm,
∴3t=42﹣3t,
解得:t=7,
∴AC=BN=4t=4×7=28cm,
综上所述,AC=18cm或AC=28cm.
【变式1-3】(2022秋 青云谱区期末)阅读理解,自主探究:
“一线三垂直”模型是“一线三等角”模型的特殊情况,即三个等角角度为90°,于是有三组边相互垂直.所以称为“一线三垂直模型”.当模型中有一组对应边长相等时,则模型中必定存在全等三角形.
(1)问题解决:如图1,在等腰直角△ABC中,∠ACB=90°,AC=BC,过点C作直线DE,AD⊥DE于D,BE⊥DE于E,求证:△ADC≌△CEB;
(2)问题探究:如图2,在等腰直角△ABC中,∠ACB=90°,AC=BC,过点C作直线CE,AD⊥CE于D,BE⊥CE于E,AD=2.5cm,DE=1.7cm,求BE的长;
(3)拓展延伸:如图3,在平面直角坐标系中,A(﹣1,0),C(1,3),△ABC为等腰直角三角形,∠ACB=90°,AC=BC,求B点坐标.
【答案】(1)证明见解析;
(2)0.8cm;
(3)(4,1).
【解答】(1)证明:∵AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∵∠ACB=90°,
∴∠ACD+∠ECB=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
(2)解:∵BE⊥CE,AD⊥CE,
∴∠ADC=∠CEB=90°,
∴∠CBE+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACD=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴AD=CE=2.5cm,CD=BE,
∴BE=CD=CE﹣DE=2.5﹣1.7=0.8(cm),
即BE的长为0.8cm;
(3)解:如图3,过点C作直线l∥x轴,交y轴于点G,过A作AE⊥l于点E,过B作BF⊥l于点F,交x轴于点H,
则∠AEC=∠CFB=∠ACB=90°,
∵A(﹣1,0),C(1,3),
∴EG=OA=1,CG=1,FH=AE=OG=3,
∴CE=EG+CG=2,
∵∠ACE+∠EAC=90°,∠ACE+∠FCB=90°,
∴∠EAC=∠FCB,
在△AEC和△CFB中,
,
∴△AEC≌△CFB(AAS),
∴AE=CF=3,BF=CE=2,
∴FG=CG+CF=1+3=4,BH=FH﹣BF=3﹣2=1,
∴B点坐标为(4,1).
【典例2】(1)猜想:如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.试猜想DE、BD、CE有怎样的数量关系,请直接写出;
(2)探究:如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α(其中α为任意锐角或钝角)如果成立,请你给出证明;若不成立,请说明理由;
(3)解决问题:如图3,F是角平分线上的一点,且△ABF和△ACF均为等边三角形,D、E分别是直线m上A点左右两侧的动点,D、E、A互不重合,在运动过程中线段DE的长度始终为n,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并说明理由.
【解答】解:(1)DE=BD+CE,
理由如下:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°,
∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,
∴DE=AD+AE=BD+CE;
(2)结论DE=BD+CE成立,
理由如下:∵∠BAD+∠CAE=180°﹣∠BAC,∠BAD+∠ABD=180°﹣∠ADB,∠ADB=∠BAC,
∴∠ABD=∠CAE,
在△BAD和△ACE中,
,
∴△BAD≌△ACE(AAS),
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE;
(3)△DFE为等边三角形,
理由如下:由(2)得,△BAD≌△ACE,
∴BD=AE,∠ABD=∠CAE,
∴∠ABD+∠FBA=∠CAE+FAC,即∠FBD=∠FAE,
在△FBD和△FAE中,
,
∴△FBD≌△FAE(SAS),
∴FD=FE,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DFE为等边三角形.
【变式2-1】(2022秋 汕尾期中)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
【答案】见试题解答内容
【解答】证明:(1)∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∵DC+CE=DE,
∴AD+BE=DE.
(2)DE=AD﹣BE,
理由:∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC﹣CD=AD﹣BE.
【变式2-2】(2022秋 东台市月考)【一线三等角模型】如图1:点A、B、C在一条直线上,∠A=∠DBE=∠C,当BD=BE时,有△ABD≌△CEB.理由:
∵∠A=∠DBE,∴∠D+∠DBA=180°﹣∠A,∠DBA+∠CBE=180°﹣∠DBE,∴∠D=∠CBE﹣﹣﹣﹣﹣﹣﹣﹣请将全等证明过程补充完整.
【模型运用】如图2:∠ABC=∠CAD=90°,AB=4,AC=AD,求△BAD的面积;
【能力提升】如图3:在等边△DEF中,A,C分别为DE、DF边上的动点,AE=2CD,连接AC,以AC为边在△DEF内作等边△ABC,连接BF,当点A从点E向点D运动(不与点D重合)时,∠CFB的度数变化吗?如不变请求出它的度数,如变化,请说明它是怎样变化的?
【答案】【一线三等角模型】证明见解析部分;
【模型运用】8;
【能力提升】∠CFB=30°.
【解答】【一线三等角模型】证明:如图1:∵∠A=∠DBE,
∴∠D+∠DBA=180°﹣∠A,∠DBA+∠CBE=180°﹣∠DBE,
∴∠D=∠CBE,
在△ABD和△CEB中,
,
∴△ABD≌△CEB(AAS);
【模型运用】解:如图2:过点D作DT⊥BA交BA的延长线于点T.
同法可证△ATD≌△CBA(AAS),
∴DT=AB=4,
∴S△ABD=×AB×DT=×4×4=8;
【能力提升】解:∠CFB=30°不变.
理由:如图3中,在CF上取一点N,使得FN=DC.
∵△ABC,△DEF都是等边三角形,
∴∠D=∠ACB=60°,DA=DF,CA=CB,
∵AE=2CD,CD=FN,
∴DA=CN,
∵∠ACN=∠ACB+∠BCN=∠D+∠CAD,
∴∠BCN=∠DAC,
在△ADC和△CNB中,
,
∴△ADC≌△CNB(SAS),
∴BN=CD,∠D=∠BNC=60°,
∵NF=CD,
∴NB=NF,
∴∠NBF=∠NFB,
∵∠BNC=∠NBF+∠NFB=60°,
∴∠NFB=∠NBF=30°,
∴∠CFB=30°.
【模型二:手拉手模型】
应用:①利用手拉手模型证明三角形全等,便于解决对应的几何问题;
②作辅助线构造手拉手模型,难度比较大。
【类型一:等边三角形中的手拉手模型】
【典例3】阅读与理解:如图1,等边△BDE按如图所示方式设置.
操作与证明:
(1)操作:固定等边△ABC,将△BDE绕点B按逆时针方向旋转120°,连接AD,CE,如图2;在图2中,请直接写出线段CE与AD之间具有怎样的大小关系.
(2)操作:若将图1中的△BDE,绕点B按逆时针方向旋转任意一个角度α(60°<α<180°),连接AD,CE,AD与CE相交于点M,连BM,如图3;在图3中线段CE与AD之间具有怎样的大小关系?∠EMD的度数是多少?证明你的结论.
猜想与发现:
(3)根据上面的操作过程,请你猜想在旋转过程中,∠DMB的度数大小是否会随着变化而变化?请证明你的结论.
【解答】解:(1)EC=AD;
∵将△BDE绕点B按逆时针方向旋转120°,
∴∠ABD=∠CBE,
在△EBC和△DBA中,
,
∴△EBC≌△DBA(SAS),
∴EC=AD;
(2)EC=AD,∠EMD=60°,理由如下:
设AD与BE交于点O,
∵将△BDE绕点B按逆时针方向旋转α度,
∴∠EBC=∠DBA=α,
∵△ABC与△BDE是等边三角形,
∴BC=AB,BD=BE,
∴△EBC≌△DBA(SAS),
∴EC=AD,∠CEB=∠ADB,
∵∠EOM=∠DOB,
∴∠EMD=∠EBD=60°,
(3)不变,理由如下:
过点B作BH⊥AD于点H,BF⊥EC于点F,
∵△EBC≌△DBA,
∴S△EBC=S△DBA,AD=EC,
∴BH=BF,
∴MB平分∠DMC,
∴∠DMB=,
∴∠DMB的度数大小不变
【变式3-1】如图,△ABC和△DCE都是等边三角形,且B,C,D三点在一条直线上,连接AD,BE相交于点P.
(1)求证:BE=AD.
(2)求∠APB的度数.
【解答】(1)证明:∵△ABC和△DCE都是等边三角形,
∴BC=AC,CE=CD,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
即∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)解:由(1)可得△ACD≌△BCE(SAS),
∴∠DAC=∠EBC.
∵∠ACB=∠DAC+∠ADC=60°,
∴∠EBC+∠ADC=∠APB=60°,
即∠APB=60°.
【变式3-1】(2023春 佛山期末)在等边△ABC中,AB=6,点D是射线CB上一点,连接AD.
(1)如图1,当点D在线段CB上时,在线段AC上取一点E,使得CE=BD,求证:AD=BE;
(2)如图2,当点D在CB延长线上时,将线段AD绕点A逆时针旋转角度θ(0°<θ<180°)得到线段AF,连接BF,CF.
①当AF位于∠BAC内部,且∠DAF恰好被AB平分时,若BD=2,求CF的长度;
②如图3,当θ=120°时,记线段BF与线段AC的交点为G,猜想DC与AG的数量关系,并说明理由.
【答案】(1)证明过程见解答;
(2)①;②证明过程见解答.
【解答】(1)证明:∵△ABC是等边三角形,
∴AB=BC=AC,
∠ABC=∠C=∠BAC=60°,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS),
∴AD=BE;
(2)解:①过点F作FH⊥BC于点H,如图2,
在△ABD和△ABF中,
,
∴△ABD≌△ABF(SAS),
∴BF=BD=2,
∠ABF=∠ABD=180°﹣∠ABC=120°,
∴∠FBH=∠ABF﹣∠ABC=60°,
在Rt△BFH中,
∠BFH=90°﹣∠FBH=30°,
∴BH=BF==1,
HF2=BF2﹣BH2=22﹣12=3,
∵CH=BC﹣BH=6﹣1=5,
∴CF2=CH2+HF2=52+3=28,
∴;
②证明:延长AC到点M,使CM等于BD,连接FM,如图3,
∵∠DAF=θ=120°,∠BAC=60°,
∴∠DAB+∠MAF=120°﹣60°=60°,
∵∠ADB+∠DAB=∠ABC=60°,
∴∠ADB=∠MAF,
又∵BC=AC,BD=CM,
∴BC+BD=AC+CM,
即:DC=AM,
在△ADC和△FAM中,
,
∴△ADC≌△FAM(SAS),
∴AC=MF,∠M=∠ACB=60°,
∴MF=AB,∠M=∠BAC,
在△ABG和△MFG中,
,
∴△ABG≌△MFG(AAS),
∴AG=MG,
∴AM=AG+MG=2AG,
∴CD=2AG.
【类型二:等腰三角形的手拉手模型】
【典例4】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上时,∠BAC=90°,
①求证:BD=CE;
②∠BCE= ;
(2)设∠BCE=a,∠BAC=β,
①如图2,当点D在线段BC上移动,求证α+β=180°;
②当点D在射线BC的反向延长线上移动,则a、β之间有怎样的数量关系?请直接写出你的结论.
【解答】(1)①证明:∵AB=AC,AD=AE,∠BAD+∠DAC=∠DAC+∠CAE=90°,
∴∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
②由①知△ABD≌△ACE,
∴∠B=∠ACE,
∴∠BCE=∠ACB+∠ACE=∠ACB+∠B,
又∵∠BAC=90°,
∴∠BCE=90°,
故答案为:90°;
(2)①证明:∵AB=AC,AD=AE,∠BAD+∠DAC=∠DAC+∠CAE,
∴∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE,
∴∠B+∠ACB=α,
∵∠BAC+∠B+∠ACB=180°,
∴α+β=180°;
②α=β.理由如下:如图,由①同理得,△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∴∠BAC+∠ACB=∠ACB+∠BCE,
∴∠BAC=∠BCE,
即α=β.
【变式4-1】如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N.
证明:(1)BD=CE;(2)BD⊥CE.
【解答】证明:(1)∵∠BAC=∠DAE=90°
∴∠BAC+∠CAD=∠DAE+∠CAD
即∠CAE=∠BAD
在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴BD=CE
(2)∵△ABD≌△ACE
∴∠ABN=∠ACE
∵∠ANB=∠CND
∴∠ABN+∠ANB=∠CND+∠NCE=90°
∴∠CMN=90°
即BD⊥CE.
【变式4-2】如图,在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点,连接AD,以AD为直角边作等腰直角三角形ADF.
(1)如图1,若当点D在线段BC上时(不与点B、C重合),证明:△ACF≌△ABD;
(2)如图2,当点D在线段BC的延长线上时,试猜想CF与BD的数量关系和位置关系,并说明理由.
【解答】(1)证明:∵∠BAC=90°,△ADF是等腰直角三角形,
∴∠CAF+∠CAD=90°,∠BAD+∠ACD=90°,
∴∠CAF=∠BAD,
在△ACF和△ABD中,
,
∴△ACF≌△ABD(SAS),
(2)解:CF=BD,CF⊥BD.
理由:∵∠CAB=∠DAF=90°,
∴∠CAB+∠CAD=∠DAF+∠CAD,
即∠CAF=∠BAD,
在△ACF和△ABD中,
,
∴△ACF≌△ABD(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠BCF=∠ACF+∠ACB=45°+45°=90°,
∴CF⊥BD
【变式4-3】(2022秋 惠民县校级期末)(1)如图1,△ABC与△ADE均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:BD=CE;
(2)如图2,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
填空:∠AEB的度数为 60° ;线段BE与AD之间的数量关系是 BE=AD .
(3)拓展探究
如图3,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
【答案】见试题解答内容
【解答】(1)证明:∵∠BAC=∠DAE=40°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△BAD和△CAE中,
∴△BAD≌△CAE,
∴BD=CE.
(2)解:∵△ACB和△DCE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∠CDE=∠CED=60°,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
∴△ACD≌△BCE,
∴BE=AD,∠ADC=∠BEC,
∵点A,D,E在同一直线上,
∴∠ADC=180°﹣60°=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC﹣∠CED=120°﹣60°=60°,
综上,可得
∠AEB的度数为60°;线段BE与AD之间的数量关系是:BE=AD.
故答案为:60°、BE=AD.
(3)解:∵△ACB和△DCE均为等腰直角三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE,
∴BE=AD,∠BEC=∠ADC,
∵点A,D,E在同一直线上,
∴∠ADC=180﹣45=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC﹣∠CED=135﹣45=90°;
∵∠DCE=90°,CD=CE,CM⊥DE,
∴CM=DM=EM,
∴DE=DM+EM=2CM,
∴AE=AD+DE=BE+2CM.
【模型二:直角三角形中的手拉手模型】
【典例5】△ABC与△BDE均为等腰直角三角形,∠ABC=∠DBE=90°.
(1)如图1,当D,B,C在同一直线时,CE的延长线与AD交于点F.求证:∠CFA=90°;
(2)当△ABC与△BDE的位置如图2时,CE的延长线与AD交于点F,猜想∠CFA的大小并证明你的结论;
(3)如图3,当A,E,D在同一直线时(A,D在点E的异侧),CE与AB交于点G,∠BAD=∠ACE,求证:BG+AB=AC.
【解答】(1)证明:∵△ABC和△DBE是等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
在△ABD和△CBE中,
,
∴△ABD≌△CBE(SAS),
∴∠BAD=∠BCE,
∵∠BAD+∠AFE+∠FEA=∠BCE+∠ABC+∠BEC=180°,
又∵∠FEA=∠BEC,
∴∠CFA=∠ABC=90°.
(2)解:∠CFA=90°.
理由如下:
同理可证△ABD≌△CBE(SAS),
∴∠BAD=∠BCE,
∴∠CFA=∠ABC=90°.
(3)过点G作GH⊥AC于点H,同(2)可知∠BAD=∠BCE,
∵∠BAD=∠ACE,
∴∠ACE=∠BCE,
∵AB⊥BC,GH⊥AC,
∴BG=GH,
∵∠BAC=45°,
∴∠BAC=∠AGH=45°,
∴GH=AH,
∴AH=BG,
在Rt△BCG和Rt△HCG中,
,
∴Rt△BCG≌Rt△HCG(HL),
∴BC=CH,
∴AC=AH+CH=BG+BC=BG+AB.
【变式5】如图:已知△ABC中,∠BAC=90°,AB=AC,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作△ADE,使∠DAE=90°,AD=AE,连接CE.
发现问题:
如图1,当点D在边BC上时,
(1)请写出BD和CE之间的位置关系为 BD⊥CE ,并猜想BC和CE、CD之间的数量关系: .
(2)如图2,当点D在边BC的延长线上且其他条件不变时,(1)中BD和CE之间的位置关系;BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
【解答】解:(1)∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ACE=∠ABD=45°,
∴∠BCE=∠ACB+∠ACE=45°+45°=90°,BC=CD+BD=CD+CE,
∴BD⊥CE,
故答案为:BD⊥CE;BC=CD+CE;
(2)BD⊥CE成立,数量关系不成立,关系为BC=CE﹣CD.
理由如下:如图2,∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ACE=∠ABC,
∴BD=BC+CD,∠ACE+∠ACB=90°,
∴BD⊥CE;BC=CE﹣CD
【模型三:作辅助线构造手拉手模型】
【典例6】在△ABC中,AB=AC,∠ABC=α,点D是直线BC上一点,点C关于射线AD的对称点为点E.作直线BE交射线AD于点F.连接CF.
(1)如图1,点D在线段BC上,补全图形,求∠AFB的大小(用含α的代数式表示);
(2)如果∠α=60°,
①如图2,当点D在线段BC上时,用等式表示线段AF,BF,CF之间的数量关系,并证明;
②如图3,当点D在线段CB的延长线上时,直接写出线段AF、BF、CF之间的数量关系.
【解答】解:(1)补全图形如下,
连接AE,
∵点E为点C关于AD的对称点,
∴AE=AC,EF=FC,∠EAD=∠CAD,
设∠EAD=∠CAD=x,
∴∠CAE=2x,
∵AB=AC,
∴∠ACB=∠ABCα.
∴∠BAE=180°﹣2x﹣2α,
∴∠ABE+∠AEB=2x+2α,
∵AE=AB,
∴∠ABE=∠AEB=x+α,
∴∠AFB=∠AEB﹣∠EAD=α;
(2)①AF=BF+CF.
延长FB至点G,使FG=FA,连接AG,
∵AB=AC,
∴∠ABC=α=60°,
∴△ABC为等边三角形,∠BAC=60°,
由(1)知∠AFB=α=60°,
∴△AFG为等边三角形,
∴AG=AF,∠GAF=60°,
∴∠GAB=∠FAC,
在△ABG和△ACF中,
,
∴△ABG≌△ACF(SAS),
∴BG=CF,
∴CF+BF=BG+BF=GF,
∵GF=AF,
∴AF=BF+CF;
②结论为:CF=AF+BF.连接AE.
∵点E为点C关于AD的对称点,
∴AE=AC,EF=FC,∠EAD=∠CAD,
设∠EAD=∠CAD=x,
∴∠CAE=2x,
∵AB=AC=AE,
∴∠ACB=∠ABC=∠BAC=60°.
∴∠DAB=x﹣60°,
∴∠EAB=x+x﹣60°=2x﹣60°,
∵AE=AB,
∴∠ABE=∠AEB==120°﹣x,
∴∠AFE=∠DAB+∠ABE=x﹣60°+120°﹣x=60°,
在BE上取点G,使得FG=FA,连接AG,
∴△AFG为等边三角形,
∴AG=AF,∠GAF=60°,
∴∠GAE=∠FAB=x﹣60°,
在△AGE与△AFB中,
,
∴△AGE≌△AFB(SAS),
∴BF=EG,
∴EF=EG+FG=BF+AF,
∴CF=EF=BF+AF.
【变式6-1】(2022秋 西湖区校级期末)已知,∠MON=90°,点A在边OM上,点P是边ON上一动点,∠OAP=α.以线段AP为边在AP上方作等边△ABP,连接OB、BP,再以线段OB为边作等边△OBC(点C、P在OB的同侧),作CH⊥ON于点H.
(1)如图1,α=60°.①依题意补全图形;②求∠BPH的度数;
(2)如图2,当点P在射线ON上运动时,用等式表示线段OA与CH之间的数量关系,并证明.
【答案】(1)①见解析;②90°;(2)OA=2CH.
【解答】解:(1)①如图所示,即为所求;
②∵△ABP是等边三角形,
∴∠BPA=60°,
∵∠OAP=α=60°,
∴∠OPA=30°,
∴∠BPH=180°﹣∠OPA﹣∠BPA=90°;
(2)OA=2CH,证明如下:
如图,连接BC,PC,
由(2)可知,△ABP是等边三角形,
∴BA=BP,∠ABP=∠BPA=60°,
∵△BOC是等边三角形,
∴BO=BC,∠BOC=60°,
∴∠ABO=60°﹣∠OBP=∠PBC,
∴△ABO≌△PBC(SAS),
∴AO=PC,∠BPC=∠BAO,
∵∠OAP=α,
∴∠BAO=∠BAP+∠OAP=60°+α,
∴∠BPC=60°+α,
∵∠BPN=180°﹣∠APO﹣∠BPA=120°﹣(90°﹣α)=30°+α,
∴∠HPC=∠BPC﹣∠BPN=30°,
∵CH⊥ON,
∴∠CHO=90°,
在Rt△CHP中,PC=2CH,
∴OA=2CH
【模型三:半角模型】等角=要三角形中得半角模型
【典例7】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.已知,△ABC中,AB=AC,∠BAC=α,点D、E在边BC上,且.
(1)如图a,当α=60°时,将△AEC绕点A顺时针旋转60°到△AFB的位置,连结DF.
①∠DAF= ;②求证:DF=DE;
(2)如图b,当α=90°时,猜想BD、DE、CE的数量关系,并说明理由.
【解答】(1)①解:由旋转知,AF=AE,∠BAF=∠CAE,∠EAF=60°,
∵∠DAE=α,∠BAC=α=60°,
∴∠DAE=×60°=30°,
∴∠CAE+∠BAD=∠BAC﹣∠DAE=30°,
∴∠DAF=∠BAD+∠BAF=∠BAD+∠CAE=30°,
故答案为:30°;
②证明:由①知,AF=AE,∠DAF=∠DAE=30°,
∵AB=AC,
∴△DAF≌△DAE(SAS),
∴DF=DE;
(2)解:DE2=BD2+CE2,理由如下:
如图,
将△AEC绕点A顺时针旋转90°到△AFB的位置,连结DF,
∴AF=AE,∠EAF=90°=∠BAC,
∴∠BAF=∠CAE,
∴△BAF≌△CAE(SAS),
∴BF=CE,∠ABF=∠ACE,
在Rt△ABC中,∠C=∠ABC=45°,
∴∠ABF=45°,
∴∠DBF=90°,根据勾股定理得,DF2=BD2+BF2,
∴DF2=BD2+CE2,
同(1)②的方法得,DF=DE,
∴DE2=BD2+CE2.
【变式7】已知∠MBN=60°,等边△BEF与∠MBN顶点B重合,将等边△BEF绕顶点B顺时针旋转,边EF所在直线与∠MBN的BN边相交于点C,并在BM边上截取AB=BC,连接AE.
(1)将等边△BEF旋转至如图①所示位置时,求证:CE=BE+AE;
(2)将等边△BEF顺时针旋转至如图②、图③位置时,请分别直接写出AE,BE,CE之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若BF=4,AE=1,则CE= 3或5 .
【解答】(1)证明:∵△BEF为等边三角形,
∴BE=EF=BF,∠EBF=60°,
∴∠EBA+∠ABF=60°,
∵∠MBN=60°,
∴∠CBF+∠ABF=60°,
∴∠EBA=∠CBF,
在△ABE与△CBF中,
,
∴△ABE≌△CBF(SAS),
∴AE=CF,
∵CE=EF+CF,
∴CE=BE+AE;
(2)解:图②结论为CE=BE﹣AE,图③结论为CE=AE﹣BE,
图②的理由如下:
∵△BEF为等边三角形,
∴BE=EF=BF,∠EBF=60°,
∴∠EBA+∠ABF=60°,
∵∠MBN=60°,
∴∠CBF+∠ABF=60°,
∴∠EBA=∠CBF,
在△ABE与△CBF中,
,
∴△ABE≌△CBF(SAS),
∴AE=CF,
∵CE=EF﹣CF,
∴CE=BE﹣AE,
图③的利用如下:
∵△BEF为等边三角形,
∴BE=EF=BF,∠EBF=60°,
∴∠EBA+∠ABF=60°,
∵∠MBN=60°,
∴∠CBF+∠ABF=60°,
∴∠EBA=∠CBF,
在△ABE与△CBF中,
,
∴△ABE≌△CBF(SAS),
∴AE=CF,
∵CE=CF﹣EF,
∴CE=AE﹣BE;
(3)解:在(1)条件下,CE=BE+AE=BF+AE=4+1=5;
在(2)条件下,CE=BE﹣AE=BF﹣AE=4﹣1=3,
综上所述,CE=3或5,
故答案为:3或5.
【变式7-2】(2021秋 桦甸市期末)如图,△ABC是等边三角形,D是边BC上一点(点D不与点B,C重合),作∠EDF=60°,使角的两边分别交边AB,AC于点E,F,且BD=CF.
(1)如图①,若DE⊥BC,则∠DFC= 90 度;
(2)如图②,D是边BC上一点(点D不与点B,C重合),求证:BE=CD;
(3)如图③,若D是边BC的中点,且AB=2,则四边形AEDF的周长为 4 .
【答案】(1)90;
(2)证明见解析;
(3)4.
【解答】解:(1)∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵DE⊥BC,即∠BDE=90°,∠EDF=60°,
∴∠BED=∠CDF=30°,
∴∠DFC=90°,
故答案为:90;
(2)∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠EDF+∠CDF=∠B+∠BED,且∠EDF=60°,
∴∠CDF=∠BED,
在△BDE和△CFD中,
,
∴△BDE≌△CFD(AAS),
∴BE=CD;
(3)∵△ABC是等边三角形,AB=2,
∴∠B=∠C=60°,AB=BC=AC=2,
∵D为BC中点,且BD=CF,
∴BD=CD=CF=AF=1,
由(2)知△BDE≌△CFD,
∴BE=CD=1,DE=DF,
∵∠B=60°,
∴△BDE是等边三角形,
∴DE=DF=1,
则四边形AEDF的周长为AE+DE+DF+AF=4,
故答案为:4.
【变式7-3】】等边△ABC,D为△ABC外一点,∠BDC=120°,BD=DC,∠MDN=60°,射线DM与直线AB相交于点M,射线DN与直线AC相交于点N,
①当点M、N在边AB、AC上,且DM=DN时,直接写出BM、NC、MN之间的数量关系.
②当点M、N在边AB、AC上,且DM≠DN时,猜想①中的结论还成立吗?若成立,请证明.
③当点M、N在边AB、CA的延长线上时,请画出图形,并写出BM、NC、MN之间的数量关系.
【解答】解①BM、NC、MN之间的数量关系 BM+NC=MN.
②猜想:结论仍然成立.
证明:在CN的反向延长线上截取CM1=BM,连接DM1.
∵∠MBD=∠M1CD=90°,BD=CD,
∴△DBM≌△DCM1,
∴DM=DM1,∠MBD=∠M1CD,M1C=BM,
∵∠MDN=60°,∠BDC=120°,
∴∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N=M1C+NC=BM+NC,
③证明:在CN上截取CM1=BM,连接DM1.
可证△DBM≌△DCM1,
∴DM=DM1,
可证∠CDN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N,
∴NC﹣BM=MN.
【模型四:对角互补模型】
应用:通过做垂线或者利用旋转构造全等三角形解决问题。
【典例9】(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图(2),在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
【解答】证明:(1)EF2=BE2+CF2,
理由如下:如图(1)延长ED到G,使DG=ED,连接CG,FG,
在△DCG与△DBE中,
,
∴△DCG≌△DBE(SAS),
∴DG=DE,CG=BE,∠B=∠DCG,
又∵DE⊥DF,
∴FD垂直平分线段EG,
∴FG=FE,
∵∠A=90°,
∴∠B+∠ACB=90°,
∴∠FCG=90°,
在△CFG中,CG2+CF2=FG2,
∴EF2=BE2+CF2;
(2)如图(2),结论:EF=EB+FC,
理由如下:延长AB到M,使BM=CF,
∵∠ABD+∠C=180°,又∠ABD+∠MBD=180°,
∴∠MBD=∠C,
在△BDM和△CDF中,
,
∴△BDM≌△CDF(SAS),
∴DM=DF,∠BDM=∠CDF,
∴∠EDM=∠EDB+∠BDM=∠EDB+∠CDF=∠CDB﹣∠EDF=120°﹣60°=60°=∠EDF,
在△DEM和△DEF中,
,
∴△DEM≌△DEF(SAS),
∴EF=EM,
∴EF=EM=BE+BM=EB+CF.
【变式9-1】(九台区期末)【教材呈现】如图是华师版八年级上册数学教材96页的部分内容.
已知:如图13.5.4,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为点D和点E.求证:PD=PE.分析:图中有两个直角三角形PDO和PEO,只要证明这两个三角形全等便可证得PD=PE.
【问题解决】请根据教材分析,结合图①写出证明PD=PE的过程.
【类比探究】
(1)如图②,OC是∠AOB的平分线,P是OC上任意一点,点M,N分别在OB和OA上,连接PM和PN,若∠PMO+∠PNO=180°,求证:PM=PN;
(2)如图③,△ABC的周长是12,BO、CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若OD=3,则△ABC的面积为 18 .
【答案】【问题解决】证明过程见解析.
【类比探究】(1)证明过程见解析.
(2)18.
【解答】【问题解决】证明:在△OPE和△OPD中,
,
∴△OPE≌△OPD(AAS),
∴PD=PE;
【类比探究】(1)证明:如图②,过点P作PE⊥OB于E,PF⊥OA于F,
∵OC是∠AOB的平分线,PE⊥OB,PF⊥OA,
∴PE=PF,
∵∠PMO+∠PME=180°,∠PMO+∠PNO=180°,
∴∠PME=∠PNO,
在△PME和△PNF中,
,
∴△PME≌△PNF(AAS),
∴PM=PN;
(2)解:过O作OE⊥AB与E,OF⊥AC于F,
∵BO、CO分别平分∠ABC和∠ACB,
∴EO=DO,OF=DO,
∵OD=3,
∴EO=FO=3,
∵△ABC的周长是12,
∴AB+BC+AC=12,
∴△ABC的面积:AB EO+AC FO+CB DO=(AB+AC+BC)=×12=18,
故答案为:18.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2023/7/13 12:18:00;用户:gaga;邮箱:18376708956;学号:18
【变式9-2】(1)阅读理解:
如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:
延长AD到点E使DE=AD,再连接BE,这样就把AB,AC,2AD集中在△ABE中,利用三角形三边的关系可判断线段AE的取值范围是 ;则中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,此时:BE+CF EF(填“>”或“=”或“<”);
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180,CB=CD,∠BCD=140°,以C为顶点作∠ECF=70°,边CE,CF分别交AB,AD于E,F两点,连接EF,此时:BE+DF EF(填“>”或“=”或“<“);
(4)若在图③的四边形ABCD中,∠ECF=α(0°<α<90°),∠B+∠D=180,CB=CD,且(3)中的结论仍然成立,则∠BCD= (用含α的代数式表示).
【解答】解:(1)在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴BE=AC=3,
在△ABE中,AB﹣BE<AE<AB+BE,
即2<AE<8,
∴2<2AD<8,
∴1<AD<4,
故答案为:2<AE<8;1<AD<4;
(2)如图,延长FD至点G,使DG=DF,连接BG,EG,
∵点D是BC的中点,
∴DB=DC,
∵∠BDG=∠CDF,DG=DF,
∴△BDG≌△CDF(SAS),
∴BG=CF,
∵ED⊥FD,FD=GD,
∴EF=EG,
在△BEG中,BE+BG>EG,
∴BE+CF>EF,
故答案为:>;
(3)BE+DF=EF,
如图,延长AB至点G,使BG=DF,连接CG,
∵∠ABC+∠D=180°,∠ABC+∠CBG=180°,
∴∠CBG=∠D,
又∵CB=CD,BG=DF,
∴△CBG≌△CDF(SAS),
∴CG=CF,∠BCG=∠DCF,
∵∠BCD=140°,∠ECF=70°,
∴∠DCF+∠BCE=70°,
∴∠BCE+∠BCG=70°,
∴∠ECG=∠ECF=70°,
又∵CE=CE,CG=CF,
∴△ECG≌△ECF(SAS),
∴EG=EF,
∵BE+BG=EG,
∴BE+DF=EF,
故答案为:=;
(4)由(3)同理可得△CBG≌△CDF,
∴CG=CF,∠BCG=∠DCF,
若BE+DF=EF,
则EG=EF,
∴△ECF≌△ECG(SSS),
∴∠ECG=∠ECF,
∴∠BCD=2∠ECF=2α,
故答案为:2α.
【典例10】(1)如图1,四边形ABCD是边长为5 cm的正方形,E,F分别在AD,CD边上,∠EBF=45°.为了求出△DEF的周长.小南同学的探究方法是:
如图2,延长EA到H,使AH=CF,连接BH,先证△ABH≌△CBF,再证△EBH≌△EBF,得EF=EH,从而得到△DEF的周长= cm;
(2)如图3,在四边形ABCD中,AB=AD,∠BAD=100°,∠B=∠ADC=90°.E,F分别是线段BC,CD上的点.且∠EAF=50°.探究图中线段EF,BE,FD之间的数量关系;
(3)如图4,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是线段BC,CD上的点,且2∠EAF=∠BAD,(2)中的结论是否仍然成立,若成立,请证明,若不成立,请说明理由;
(4)若在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别在CB、DC的延长线上,且2∠EAF=∠BAD,请画出图形,并直接写出线段EF、BE、FD之间的数量关系.
【解答】解:(1)如图1,延长EA到H,使AH=CF,连接BH,
∵四边形ABCD是正方形,
∴AB=BC=AD=CD=5cm,∠BAD=∠BCD=90°,
∴∠BAH=∠BCF=90°,
又∵AH=CF,AB=BC,
∴△ABH≌△CBF(SAS),
∴BH=BF,∠ABH=∠CBF,
∵∠EBF=45°,
∴∠CBF+∠ABE=45°=∠HBA+∠ABE=∠EBF,
∴∠EBH=∠EBF,
又∵BH=BF,BE=BE,
∴△EBH≌△EBF(SAS),
∴EF=EH,
∴EF=EH=AE+CF,
∴△DEF的周长=DE+DF+EF=DE+DF+AE+CF=AD+CD=10(cm).
故答案为:10.
(2)EF=BE+DF.
证明:如图2所示,延长FD到点G.使DG=BE.连接AG,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠BAD=100°,∠EAF=50°,
∴∠BAE+∠FAD=∠DAG+∠FAD=50°,
∴∠EAF=∠FAG=50°,
在△EAF和△GAF中,
,
∴△EAF≌△GAF(SAS),
∴EF=FG=DF+DG,
∴EF=BE+DF;
(3)成立.
证明:如图3,延长EB到G,使BG=DF,连接AG.
∵∠ABC+∠D=180°,∠ABG+∠ABC=180°,
∴∠ABG=∠D,
∵在△ABG与△ADF中,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠BAG=∠DAF,
∵2∠EAF=∠BAD,
∴∠DAF+∠BAE=∠BAG+∠BAE=∠BAD=∠EAF,
∴∠GAE=∠EAF,
又AE=AE,
∴△AEG≌△AEF(SAS),
∴EG=EF,
∵EG=BE+BG,
∴EF=BE+FD;
(4)EF=DF﹣BE,
理由如下:在DF上截取DH,使DH=BE,
∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,
∴∠ABE=∠ADH,且AB=AD,DH=BE,
∴△ABE≌△ADH(SAS),
∴∠BAE=∠DAH,AH=AE,
∵∠EAF=∠BAD,
∴∠DAH+∠BAF=∠BAD,
∴∠HAF=∠BAD=∠EAF,且AF=AF,AE=AH,
∴△FAH≌△FAE(SAS),
∴HF=EF,
∴EF=HF=DF﹣DH=DF﹣BE
【变式10-1】如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,求证:EF=BE+FD.
【解答】证明:延长CB至M,使BM=FD,连接AM,如图所示:
∵∠ABC+∠D=180°,∠ABM+∠ABC=180°,
∴∠ABM=∠D,
在△ABM与△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AF=AM,∠BAM=∠DAF,
∵∠EAF=∠BAD,
∴∠DAF+∠BAE=∠BAD=∠FAE,
∴∠BAM+∠BAE=∠EAF,
即∠MAE=∠EAF,
在△AME与△AFE中,
,
∴△AME≌△AFE(SAS),
∴EF=ME,
∵ME=BE+BM,
∴EF=BE+FD.
【变式10-2】“截长补短法”证明线段的和差问题:
先阅读背景材料,猜想结论并填空,然后做问题探究.
背景材料:
(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.探究的方法是,延长FD到点G.使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出的结论是 .
探索问题:
(2)如图2,若四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立?成立的话,请写出推理过程.
【解答】证明:(1)在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为:EF=BE+DF.
(2)解:结论EF=BE+DF仍然成立;
理由:延长FD到点G.使DG=BE.连接AG,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF.
【模型五:平行+线段中点构造全等模型】
【结论】如图,AB∥CD,点E、F分别在直线AB、CD上,点O为EF中点,则△POE≌△QOF
口诀:有中点,有平行,轻轻延长就能行
【典例11】已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图③.写出AF、EF与AB的数量关系,并对图②进行证明.
【解答】(1)证明:如图①,延长AD、EF交于点G,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠G=∠BAD,
∴∠G=∠CAD,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(AAS),
∴AB=GE,
∵GE=FG+EF=AF+EF,
∴AF+EF=AB;
(2)结论:AF﹣EF=AB.
证明:如图②,延长AD、EF交于点G,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠G=∠BAD,
∴∠G=∠CAD,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(AAS),
∴AB=GE,
∵GE=FG﹣EF=AF﹣EF,
∴AF﹣EF=AB;
(3)结论:EF﹣AF=AB.
证明:如图③,延长AD交EF于点G,
∵AD平分∠PAC,
∴∠PAD=∠CAD,
∵EF∥AB,
∴∠AGF=∠PAD,
∴∠AGF=∠CAD,∠ABD=∠GED,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(ASA),
∴AB=GE,
∵EF﹣FG=GE,
∴EF﹣AF=AB;
【变式11-1】如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA⊥OC.
(1)求证:CO平分∠ACD;
(2)求证:AB+CD=AC.
【解答】解:
(1)如图,延长AO交CD的延长线于点E,
∵O为BD的中点,
∴BO=DO,
在△AOB与△EOD中,
∴△AOB≌△EOD,(ASA)
∴AO=AE,
又∵OA⊥OC,
∴AC=CE
∴CO平分∠ACD;(三线合一)
(2)由△AOB≌△EOD
可得AB=DE
∴AB+CD=CD+DE=CE
∵AC=CE
∴AB+CD=AC
【变式11-2】如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,求证AD和BC的关系。
【解答】解:如图,延长AE交BC于F.
∵AB⊥BC,AB⊥AD,
∴AD∥BC
∴∠D=∠C,∠DAE=∠CFE,
又∵点E是CD的中点,
∴DE=CE.
∵在△AED与△FEC中,
,
∴△AED≌△FEC(AAS),
∴AE=FE,AD=FC.
∵AD=5,BC=10.
∴BF=5
∴AD=
19.(2023春 青秀区校级期末)已知平行四边形ABCD,E为BC边上的中点.
(1)如图1,若BC=2CD,求证:DE平分∠ADC;
(2)若F为AB边上一点,连结DF,EF;
①如图2,若S△EFB=1,S△CDE=4,求S△DEF;
②如图3,若∠EFB+∠CDE=90°,请你写出线段AF,BF,DF之间的数量关系,并证明.
【答案】(1)见解析;
(2)①S△DEF=5;
②DF=AF+2BF,证明见解析.
【解答】(1)证明:∵E为BC的中点,
∴BC=2BE=2CE,
∵BC=2CD,
∴CD=CD,
∴∠CDE=∠CED,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠ADE=∠CED,
∴∠ADE=∠CDE,
∴DE平分∠ADC;
(2)①解:延长FE,交DC延长线于点G,如图,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠FBE=∠GCE,∠BFE=∠CGE,
∵E为BC的中点,
∴BE=CE,
在△BEF和△CEG中,
,
∴△BEF≌△CEG(AAS),
∴EF=EG,S△BEF=S△CEG,
∵S△EFB=1,S△CDE=4,
∴S△CEG=1,
S△DEG=S△CDE+S△CEG=4+1=5,
∵EF=EG,
∴S△DEF=S△DEG=5;
②DF=AF+2BF,证明如下:
延长FE,交DC延长线于点G,如图,
由①可知,△BEF≌△CEG,
∴EF=EG,BF=CG,∠EFB=∠EGC,
∵∠EFB+∠CDE=90°,
∴∠EGD+∠GDE=90°,即DE⊥FG,
∴△DFG为等腰三角形,DF=DG,
∴DF=DG=CD+CG=AB+BF=AF+BF+BF=AF+2BF,
即DF=AF+2BF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
