八上第一章三角形的初步知识专题-专题06 倍长中线法与截长补短法构造全等三形(两大类型)(含解析)
文档属性
| 名称 | 八上第一章三角形的初步知识专题-专题06 倍长中线法与截长补短法构造全等三形(两大类型)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 11:13:16 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题06 倍长中线法与截长补短法构造全等三形(两大类型)
重难点题型归纳
【题型一:倍长中线法构造全等三角形】
【题型二:截长补短法构造全等三角形】
【题型一:倍长中线法构造全等三角形】
△ABC中 , AD是BC边中线
方式1:直接倍长 延长AD到E,使DE=AD,连接BE
方式2:间接倍长
(1)作CF⊥AD于F,作BE⊥AD的延长线于E (2)延长MD到N,使DN=MD,连接CN
倍长中线法原理:
延长边上(不一定是底边)的中线,使所延长部分与中线相等,然后往往需要连接相应的顶点,则 对应角 对应边都对应相等。 此法常用于构造 全等三角形 ,利用中线的性质、 辅助线 、 对顶角 一般用“ SAS ”证明对应边之间的关系。(在一定范围中)
边上(不一定是底边)的中线,使所延长部分与中线相等,然后往往需要连接相
【典例1】为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小丽在组内做了如下尝试:如图1,在△ABC中,AD是BC边上的中线,延长AD到M,使DM=AD,连接BM.
【探究发现】:(1)图1中AC与BM的数量关系是 ,位置关系是 ;
【初步应用】:(2)如图2,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.(提示:不等式的两边都乘或除以同一个正数,不等号的方向不变.例如:若3x<6,则x<2.)
【探究提升】:(3)如图3,AD是△ABC的中线,过点A分别向外作AE⊥AB、AF⊥AC,使得AE=AB,AF=AC,延长DA交EF于点P,判断线段EF与AD的数量关系和位置关系,请说明理由.
【变式1-1】如图,已知AD是△ABC中BC边上的中线,AB=5,AC=3,则AD的取值范围是( )
A.2<AD<8 B.1<AD<4 C.2<AD<5 D.4≤AD≤8
【变式1-3】如图所示,AD为△ABC中线,D为BC中点,AE=AB,AF=AC,连接EF,EF=2AD.若△AEF的面积为3,则△ADC的面积为 .
【变式1-4】如图所示,D是△ABC边BC的中点,E是AD上一点,满足AE=BD=DC,FA=FE.求∠ADC的度数.
【变式1-6】已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE.
【变式1-5】(1)在△ABC中,AB=5,AC=3,求BC边上的中线AD的取值范围.
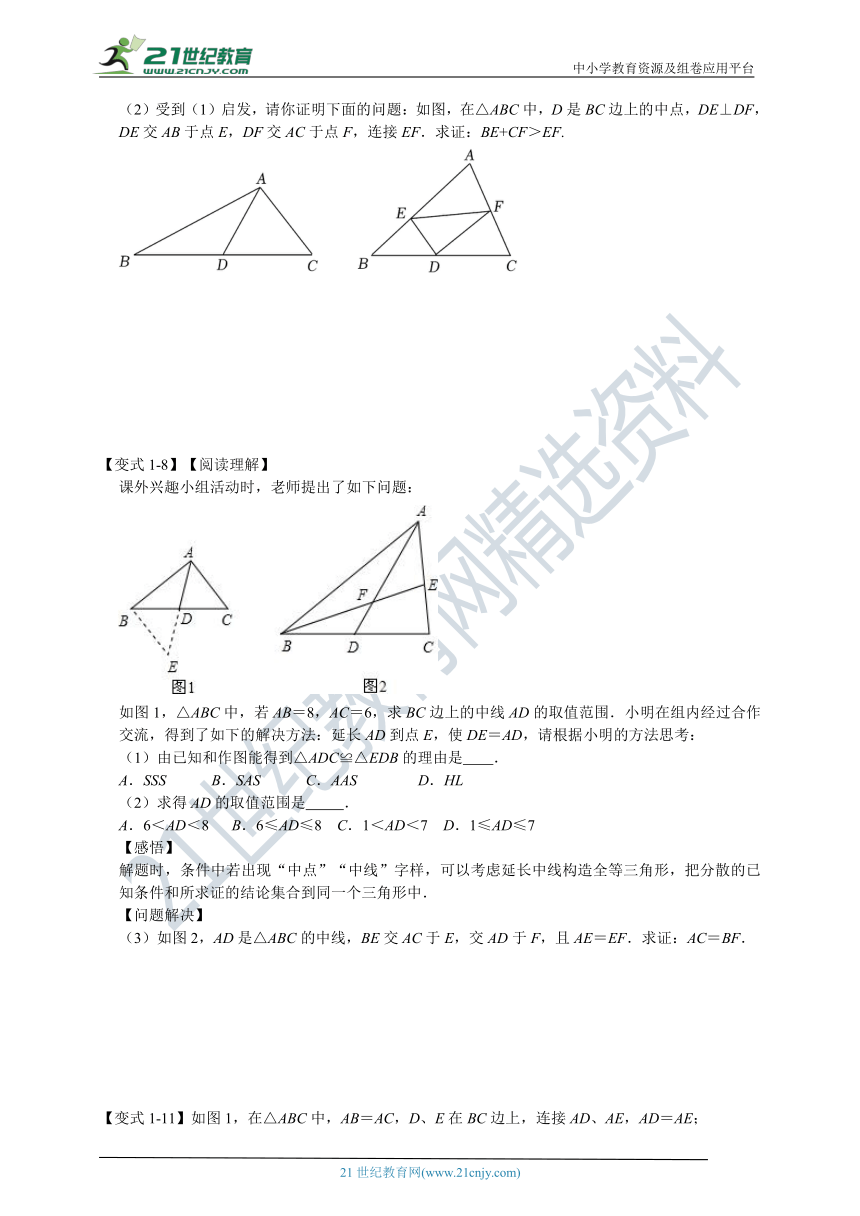
(2)受到(1)启发,请你证明下面的问题:如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.求证:BE+CF>EF.
【变式1-8】【阅读理解】
课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB的理由是 .
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是 .
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
【感悟】
解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
(3)如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC=BF.
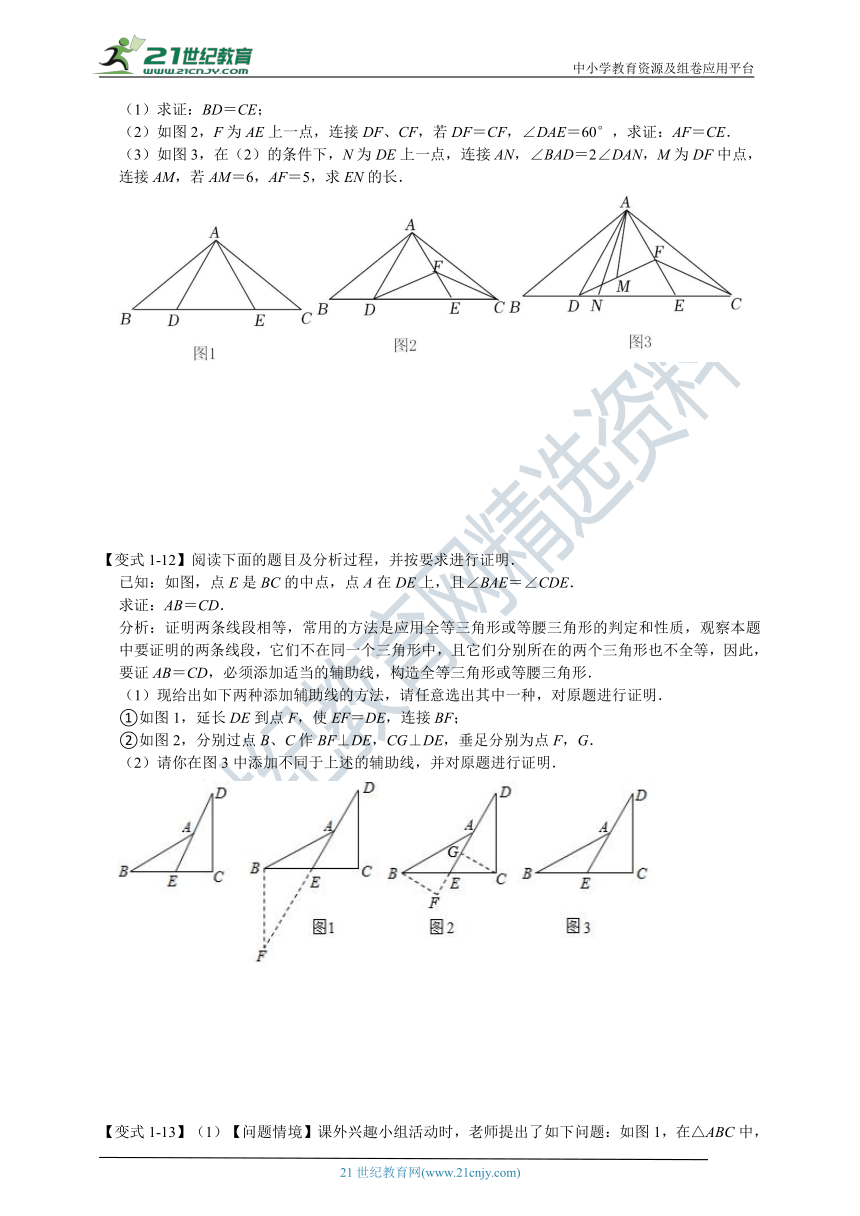
【变式1-11】如图1,在△ABC中,AB=AC,D、E在BC边上,连接AD、AE,AD=AE;
(1)求证:BD=CE;
(2)如图2,F为AE上一点,连接DF、CF,若DF=CF,∠DAE=60°,求证:AF=CE.
(3)如图3,在(2)的条件下,N为DE上一点,连接AN,∠BAD=2∠DAN,M为DF中点,连接AM,若AM=6,AF=5,求EN的长.
【变式1-12】阅读下面的题目及分析过程,并按要求进行证明.
已知:如图,点E是BC的中点,点A在DE上,且∠BAE=∠CDE.
求证:AB=CD.
分析:证明两条线段相等,常用的方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等,因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.
(1)现给出如下两种添加辅助线的方法,请任意选出其中一种,对原题进行证明.
①如图1,延长DE到点F,使EF=DE,连接BF;
②如图2,分别过点B、C作BF⊥DE,CG⊥DE,垂足分别为点F,G.
(2)请你在图3中添加不同于上述的辅助线,并对原题进行证明.
【变式1-13】(1)【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,在△ABC中,若AB=13,AC=9,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法,延长AD至点E,使DE=AD,连接BE,容易证得△ADC≌△EDB,再由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
(2)【初步运用】如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且∠FAE=∠AFE.若AE=4,EC=3,求线段BF的长.
(3)【拓展提升】如图3,在△ABC中,D为BC的中点,DE⊥DF分别交AB,AC于点E,F.求证:BE+CF>EF.
【变式1-16】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.其中一定成立是 (填序号).
【变式1-19】(1)阅读理解:
如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 ;
(2)问题解决:如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,以C为顶点作∠ECF,使得角的两边分别交AB,AD于E、F两点,连接EF,且EF=BE+DF,试探索∠ECF与∠A之间的数量关系,并加以证明.
【模型二:截长补短法构造全等三角形】
截长:1.过某一点作长边的垂线;2.在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等。
补短:1.延长短边;2.通过旋转等方式使两短边拼合到一起
【典例2】阅读下面材料:
小明遇到这样一个问题:
如图1,在△ABC中,AD平分∠BAC,∠ABC=2∠C.求证:AC=AB+BD;
小明通过思考发现,可以通过“截长、补短”两种方法解决问题:
方法一:如图2,在AC上截取AE,使得AE=AB,连接DE,可以得到全等三角形,进而解决问题.
方法二:如图3,延长AB到点E,使得BE=BD,连接DE,可以得到等腰三角形,进而解决问题.
(1)根据阅读材料,任选一种方法证明AC=AB+BD,根据自己的解题经验或参考小明的方法,解决下面的问题;
(2)如图4,四边形ABCD中,E是BC上一点,EA=ED,∠DCB=2∠B,∠DAE+∠B=90°,探究DC、CE、BE之间的数量关系,并证明.
【变式2-1】阅读:探究线段的和.差.倍.分关系是几何中常见的问题,解决此类问题通常会用截长法或补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明.
(1)请完成下题的证明过程:如图1,在△ABC中,∠B=2∠C,AD平分∠BAC.求证:AB+BD=AC.证明:在AC上截取AE=AB,连接DE
(2)如图2,AD∥BC,EA,EB分别平分∠DAB,∠CBA,CD过点E,求证:AB=AD+BC.
【变式2-2】在“教、学、练、评一体化”学习活动手册中,全等三角形专题复习课,学习过七种作辅助线的方法,其中有“截长补短”作辅助线的方法.
截长法:在较长的线段上截取一条线段等于较短线段;
补短法:延长较短线段和较长线段相等.
这两种方法统称截长补短法.
请用这两种方法分别解决下列问题:
已知,如图,在△ABC中,AB>AC,∠1=∠2,P为AD上任一点,
求证:AB﹣AC>PB﹣PC.
【变式2-3如图1,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)直接写出∠AFC的度数: ;
(2)请你判断并写出FE与FD之间的数量关系;
(3)如图2,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,试判断线段AE、CD与AC之间的数量关系并说明理由.
专题06 倍长中线法与截长补短法构造全等三形(两大类型)
重难点题型归纳
【题型一:倍长中线法构造全等三角形】
【题型二:截长补短法构造全等三角形】
【题型一:倍长中线法构造全等三角形】
△ABC中 , AD是BC边中线
方式1:直接倍长 延长AD到E,使DE=AD,连接BE
方式2:间接倍长
(1)作CF⊥AD于F,作BE⊥AD的延长线于E (2)延长MD到N,使DN=MD,连接CN
倍长中线法原理:
延长边上(不一定是底边)的中线,使所延长部分与中线相等,然后往往需要连接相
【典例1】为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小丽在组内做了如下尝试:如图1,在△ABC中,AD是BC边上的中线,延长AD到M,使DM=AD,连接BM.
【探究发现】:(1)图1中AC与BM的数量关系是 AC=BM ,位置关系是 AC∥BM ;
【初步应用】:(2)如图2,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.(提示:不等式的两边都乘或除以同一个正数,不等号的方向不变.例如:若3x<6,则x<2.)
【探究提升】:(3)如图3,AD是△ABC的中线,过点A分别向外作AE⊥AB、AF⊥AC,使得AE=AB,AF=AC,延长DA交EF于点P,判断线段EF与AD的数量关系和位置关系,请说明理由.
【答案】(1)AC=BM,AC∥BM;
(2)2<AD<10;
(3)EF=2AD,EF⊥AD,理由见解析.
【解答】解:(1)∵AD是△ABC的中线,
∴BD=CD,
在△ADC和△MDB中,
,
∴△ADC≌△MDB(SAS),
∴AC=BM,∠CAD=∠M,
∴AC∥BM,
故答案为:AC=BM,AC∥BM;
(2)如图2,延长AD到M,使DM=AD,连接BM,
由(1)可知,△MDB≌△ADC(SAS),
∴BM=AC=8,
在△ABM中,AB﹣BM<AM<AB+BM,
∴12﹣8<AM<12+8,
即4<2AD<20,
∴2<AD<10,
即BC边上的中线AD的取值范围为2<AD<10;
(3)EF=2AD,EF⊥AD,理由如下:
如图3,延长AD到M,使得DM=AD,连接BM,
由(1)可知,△BDM≌△CDA(SAS),
∴BM=AC,
∵AC=AF,
∴BM=AF,
由(2)可知,AC∥BM,
∴∠BAC+∠ABM=180°,
∵AE⊥AB、AF⊥AC,
∴∠BAE=∠FAC=90°,
∴∠BAC+∠EAF=180°,
∴∠ABM=∠EAF,
在△ABM和△EAF中,
,
∴△ABM≌△EAF(SAS),
∴AM=EF,∠BAM=∠E,
∵AD=DM,
∴AM=2AD,
∴EF=2AD,
∵∠EAM=∠BAM+∠BAE=∠E+∠APE,
∴∠APE=∠BAE=90°,
∴EF⊥AD.
【变式1-1】如图,已知AD是△ABC中BC边上的中线,AB=5,AC=3,则AD的取值范围是( )
A.2<AD<8 B.1<AD<4 C.2<AD<5 D.4≤AD≤8
【答案】B
【解答】解:如图,延长AD到E,使DE=AD,连接CE,
∵AD是BC边上的中线,
∴BD=CD,
在△ABD和△ECD中,
,
∴△ABD≌△ECD(SAS),
∴CE=AB=5,
在△ACE中,由三角形的三边关系得:CE﹣AC<AE<CE+AC,
∴5﹣3<AE<5+3,
即2<2AD<8,
∴1<AD<4,
故选:B.
【变式1-3】如图所示,AD为△ABC中线,D为BC中点,AE=AB,AF=AC,连接EF,EF=2AD.若△AEF的面积为3,则△ADC的面积为 1.5 .
【答案】1.5.
【解答】解:延长AD到点G,使DG=AD,连接BG,
∵D为BC中点,
∴△ADC的面积=△ADB的面积,BD=DC,
∵∠ADC=∠GDB,
∴△ADC≌△GDB(SAS),
∴△ADC的面积=△BDG的面积,BG=AC,
∵AC=AF,
∴BG=AF,
∵EF=2AD,AG=2AD,
∴EF=AG,
∵AE=AB,
∴△AEF≌△BGA(SSS),
∴△AEF的面积=△ABG的面积=3,
∴△ADC的面积=△BDG的面积=△ABD的面积=△ABG的面积=1.5,
故答案为:1.5.
【变式1-4】如图所示,D是△ABC边BC的中点,E是AD上一点,满足AE=BD=DC,FA=FE.求∠ADC的度数.
【答案】60°.
【解答】解:延长AD至G,使AD=DG,连接BG,在DG上截取DH=DC,
在△ADC和△GDB中,,
∴△ADC≌△GDB(SAS),
∴AC=BG,∠G=∠CAD,
∵FA=FE,
∴∠CAD=∠AEF,
∴∠G=∠CAD=∠AEF=∠BED,
∴BG=BE=AC,
∵AE=DC=BD,
∴AE+ED=DH+ED,
∴AD=EH,
在△DAC和△HEB中,
,
∴△DAC≌△HEB(SAS),
∴CD=BH,
∴BD=BH=DH,
∴△BDH为等边三角形,
∴∠C=∠BDH=60°=∠ADC.
故答案为:60°.
【变式1-6】已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE.
【答案】证明见解析.
【解答】证明:延长AE到F,使EF=AE,连接DF,
∵AE是△ABD的中线,
∴BE=ED,
在△ABE与△FDE中
,
∴△ABE≌△FDE(SAS),
∴AB=DF,∠BAE=∠EFD,
∵∠ADB是△ADC的外角,
∴∠DAC+∠ACD=∠ADB=∠BAD,
∴∠BAE+∠EAD=∠BAD,∠BAE=∠EFD,
∴∠EFD+∠EAD=∠DAC+∠ACD,
∴∠ADF=∠ADC,
∵AB=DC,∴DF=DC,
在△ADF与△ADC中
,
∴△ADF≌△ADC(SAS)
∴∠C=∠AFD=∠BAE.
【变式1-5】(1)在△ABC中,AB=5,AC=3,求BC边上的中线AD的取值范围.
(2)受到(1)启发,请你证明下面的问题:如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.求证:BE+CF>EF.
【答案】(1)1<AD<4;
(2)证明过程见解答.
【解答】解:(1)延长AD到点E,使DE=AD,连接BE,
∵AD是BC边的中线,
∴BD=DC,
∵∠ADC=∠BDE,
∴△ADC≌△EDB(SAS),
∴BE=AC=3,
在△ABC中,AB=5,
∴5﹣3<AE<5+3,
∴2<AE<8,
∴2<2AD<8,
∴1<AD<4;
(2)延长FD到点G,使GD=DF,连接BG,EG,
∵D是BC边上的中点,
∴BD=DC,
∵∠BDG=∠CDF,
∴△BDG≌△CDF(SAS),
∴BG=CF,
∵DE⊥DF,
∴ED是GF的垂直平分线,
∴EG=EF,
在△BEG中,BE+BG>EG,
∴BE+CF>EF.
【变式1-8】【阅读理解】
课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB的理由是 B .
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是 C .
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
【感悟】
解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
(3)如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC=BF.
【答案】见试题解答内容
【解答】(1)解:∵在△ADC和△EDB中
,
∴△ADC≌△EDB(SAS),
故选B;
(2)解:∵由(1)知:△ADC≌△EDB,
∴BE=AC=6,AE=2AD,
∵在△ABE中,AB=8,由三角形三边关系定理得:8﹣6<2AD<8+6,
∴1<AD<7,
故选C.
(3)证明:
延长AD到M,使AD=DM,连接BM,
∵AD是△ABC中线,
∴CD=BD,
∵在△ADC和△MDB中
∴△ADC≌△MDB,
∴BM=AC,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC,
即AC=BF.
【变式1-11】如图1,在△ABC中,AB=AC,D、E在BC边上,连接AD、AE,AD=AE;
(1)求证:BD=CE;
(2)如图2,F为AE上一点,连接DF、CF,若DF=CF,∠DAE=60°,求证:AF=CE.
(3)如图3,在(2)的条件下,N为DE上一点,连接AN,∠BAD=2∠DAN,M为DF中点,连接AM,若AM=6,AF=5,求EN的长.
【答案】(1)(2)证明见解析部分.
(3)7.
【解答】(1)证明:如图1中,过点A作AH⊥BC于点H.
∵AB=AC,AD=AE,AH⊥BC,
∴BH=CH,DH=EH,
∴BD=CE,
∴BD+DE=EC+DE,即BE=CD;
(2)证明:过点F作FT∥DE交AD于点T.
∵AD=AE,∠DAE=60°,
∴△ADE是等边三角形,
∴∠ADE=∠AED=60°,
∵FT∥DE,
∴∠ATF=∠ADE=60°,∠AFT=∠AED=60°,
∴△AFT是等边三角形,
∴AT=AF=FT,
∵AD=AE,
∴DT=EF,
∵FD=FC,
∴∠FDC=∠FCD=∠DFT,
∵∠DTF=∠CEF=120°,
∴△FTD≌△CEF(AAS),
∴FT=CE,
∴AF=EC;
(3)解:如图3中,延长AM到Q,使得MQ=AM,则AQ=2AM=12,设∠DAN=α,则∠BAD=∠CAE=2α.
∴∠B=60°﹣2α,
∴∠CNA=∠B+∠BAN=60°﹣2α+3α=60°+α,∠CAN=∠CAE+∠EAN=2α+60°﹣α=60°+α,
∴∠CNA=∠CAN,
∴CN=CA,
∵MA=MQ,∠AMF=∠QMD,MF=MD,
∴△MAF≌△MQD(SAS),
∴AF=DQ,∠MAF=∠Q,
∴DQ∥AE,
∴∠ADQ=180°﹣∠DAE=120°,
∵∠ADE=60°,
∴∠ADB=180°﹣∠ADE=120°,
∴∠ADB=∠ADQ=120°,
∵BD=EC=AF=5,
∴DB=DQ,
∵AD=AD,
∴△ADB≌△ADQ(SAS),
∴AB=AQ=12,
∴AC=AB=CN=12,
∴EN=12﹣5=7.
【变式1-12】阅读下面的题目及分析过程,并按要求进行证明.
已知:如图,点E是BC的中点,点A在DE上,且∠BAE=∠CDE.
求证:AB=CD.
分析:证明两条线段相等,常用的方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等,因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.
(1)现给出如下两种添加辅助线的方法,请任意选出其中一种,对原题进行证明.
①如图1,延长DE到点F,使EF=DE,连接BF;
②如图2,分别过点B、C作BF⊥DE,CG⊥DE,垂足分别为点F,G.
(2)请你在图3中添加不同于上述的辅助线,并对原题进行证明.
【答案】(1)(2)(3)证明见解答.
【解答】证明:(1)①如图1,延长DE到点F,使EF=DE,连接BF,
∵点E是BC的中点,
∴BE=CE,
在△BEF和△CED中,
,
∴△BEF≌△CED(SAS),
∴BF=CD,∠F=∠CDE,
∵∠BAE=∠CDE,
∴∠BAE=∠F,
∴AB=BF,
∴AB=CD;
②如图2,分别过点B、C作BF⊥DE,CG⊥DE,垂足分别为点F,G,
∴∠F=∠CGE=∠CGD=90°,
∵点E是BC的中点,
∴BE=CE,
在△BEF和△CEG中,
,
∴△BEF≌△CEG(AAS),
∴BF=CG,
在△BAF和△CDG中,
,
∴△BAF≌△CDG(AAS),
∴AB=CD;
(2)如图3,
过C点作CM∥AB,交DE的延长线于点M,
则∠BAE=∠EMC,
∵E是BC中点,
∴BE=CE,
在△BAE和△CME中,
,
∴△BAE≌△CME(AAS),
∴CM=AB,∠BAE=∠M,
∵∠BAE=∠EDC,
∴∠M=∠EDC,
∴CM=CD,
∴AB=CD.
【变式1-13】(1)【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,在△ABC中,若AB=13,AC=9,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法,延长AD至点E,使DE=AD,连接BE,容易证得△ADC≌△EDB,再由“三角形的三边关系”可求得AD的取值范围是 2<AD<11 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
(2)【初步运用】如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且∠FAE=∠AFE.若AE=4,EC=3,求线段BF的长.
(3)【拓展提升】如图3,在△ABC中,D为BC的中点,DE⊥DF分别交AB,AC于点E,F.求证:BE+CF>EF.
【答案】(1)2<AD<11;(2)7;(3)证明见解答.
【解答】(1)解:延长AD至点E,使DE=AD,连接BE,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
∴BE=AC=9,
∵AB﹣BE<AE<AB+BE,
∴4<AE<22
∴2<AD<11,
故答案为:2<AD<11.
(2)延长AD到M,使AD=DM,连接BM,如图2,
∵AD是△ABC中线,
∴BD=DC,
在△ADC和△MDB中,
,
∴△ADC≌△MDB(SAS),
∴BM=AC,∠CAD=∠M,
∵∠AFE=∠AEF,
∴AE=EF=4,
∴AC=AE+CE=7,
∴BM=AC=7,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC,
即AC=BF=7;
(3)证明:如图3,延长ED到点G,使GD=ED,连接CG、GF,
∵D是BC边上的中点,
∴CD=BD,
在△CDG和△BDE中,
,
∴△CDG≌△BDE(SAS),
∴CG=BE,
∵CG+CF>GF,
∴BE+CF>GF,
∵DE⊥DF,GD=ED,
∴DF垂直平分EG,
∴GF=EF,
∴BE+CF>EF.
【变式1-16】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.其中一定成立是 ①②④ (填序号).
【答案】见试题解答内容
【解答】解:(1)①延长FD到G,使得DG=DF,连接BG、EG.(或把△CFD绕点D逆时针旋转180°得到△BGD),
∴CF=BG,DF=DG,
∵DE⊥DF,
∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF.
②若∠A=90°,则∠EBC+∠FCB=90°,
由①知∠FCD=∠DBG,EF=EG,
∴∠EBC+∠DBG=90°,即∠EBG=90°,
∴在Rt△EBG中,BE2+BG2=EG2,
∴BE2+CF2=EF2;
(2):①∵F是AD的中点,
∴AF=FD,
∵在 ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF=∠BCD,故此选项正确;
②延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=EF=FM,故②正确;
③∵EF=FM,
∴S△EFC=S△CFM,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误;
④设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°﹣x,
∴∠EFC=180°﹣2x,
∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x,
∵∠AEF=90°﹣x,
∴∠DFE=3∠AEF,故此选项正确.
故答案为①②④.
【变式1-19】(1)阅读理解:
如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 1<AD<4 ;
(2)问题解决:如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,以C为顶点作∠ECF,使得角的两边分别交AB,AD于E、F两点,连接EF,且EF=BE+DF,试探索∠ECF与∠A之间的数量关系,并加以证明.
【答案】见试题解答内容
【解答】解:(1)阅读理解:
∵AD=DE,CD=BD,∠ADC=∠BDE,
∴△ADC≌△EDB(SAS)
∴AC=BE=3,
∵在△ABE中,AB﹣BE<AE<AB+BE
∴2<2AD<8,
∴1<AD<4,
故答案为:1<AD<4;
(2)问题解决:
解:(1)延长FD到G,使得DG=DF,连接BG、EG.
∵CD=DB,DF=DG,∠CDF=∠BDG,
∴△CDF≌△BDG(SAS)
∴CF=BG,
∵DE⊥DF,
∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF;
(3)问题拓展:∴∠A+2∠ECF=180°,
理由如下:延长AB至点N,使BN=DF,连接CN,
∵∠ABC+∠D=180°,∠ABC+∠CBN=180°,
∴∠D=∠CBN,且CD=CB,DF=BN,
∴△CDF≌△CBN(SAS)
∴CF=CN,
∵EF=BE+DF,
∴EF=BE+BN=EN,
在△CEF和△CEN中,
,
∴△CEF≌△CEN(SSS)
∴∠FCE=∠NCE=∠FCN=∠DCB,
∵∠ABC+∠D=180°,
∴∠A+2∠ECF=180°.
【模型二:截长补短法构造全等三角形】
【典例2】阅读下面材料:
小明遇到这样一个问题:
如图1,在△ABC中,AD平分∠BAC,∠ABC=2∠C.求证:AC=AB+BD;
小明通过思考发现,可以通过“截长、补短”两种方法解决问题:
方法一:如图2,在AC上截取AE,使得AE=AB,连接DE,可以得到全等三角形,进而解决问题.
方法二:如图3,延长AB到点E,使得BE=BD,连接DE,可以得到等腰三角形,进而解决问题.
(1)根据阅读材料,任选一种方法证明AC=AB+BD,根据自己的解题经验或参考小明的方法,解决下面的问题;
(2)如图4,四边形ABCD中,E是BC上一点,EA=ED,∠DCB=2∠B,∠DAE+∠B=90°,探究DC、CE、BE之间的数量关系,并证明.
【答案】见试题解答内容
【解答】(1)证明:方法一:∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△BAD和△EAD中
∴△ABD≌△AED(SAS)
∴BD=ED,∠AED=∠B=2∠C,
∵∠AED=∠C+∠EDC,
∴∠EDC=∠C,
∴ED=EC,
∴BD=EC,
∴AC=AB+BD;
(2)DC、CE、BE之间的数量关系是BE=DC+CE,
证明:在EB上截取EF,使得EF=DC,连接AF,
∵EA=ED,
∴∠EAD=∠EDA,
∴2∠DAE=180°﹣∠AED,
∵∠DAE+∠B=90°,
∴2∠DAE+2∠B=180°,
∴∠AED=2∠B=∠C,
∵∠BED=∠CDE+∠DAE,
∴∠AEB=∠CDE,
在△AEF和△EDC中
∴△AEF≌△EDC(SAS),
∴EC=AF∠AFE=∠C=2∠B,
∵∠AFE=∠B+∠BAF,
∴∠ABF=∠BAF,
∴BF=AF,
∴BF=CE,
∴BE=DC+CE.
【变式2-1】阅读:探究线段的和.差.倍.分关系是几何中常见的问题,解决此类问题通常会用截长法或补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明.
(1)请完成下题的证明过程:如图1,在△ABC中,∠B=2∠C,AD平分∠BAC.求证:AB+BD=AC.证明:在AC上截取AE=AB,连接DE
(2)如图2,AD∥BC,EA,EB分别平分∠DAB,∠CBA,CD过点E,求证:AB=AD+BC.
【答案】见试题解答内容
【解答】证明:在AC上截取AE=AB,连接DE,如图1:
∵AD平分∠BAC,
∴∠BAD=∠DAC,
在△ABD和△AED中,
,
∴△ABD≌△AED(SAS),
∴∠B=∠AED,BD=DE,又∠B=2∠C,
∴∠AED=2∠C,
而∠AED=∠C+∠EDC=2∠C,
∴∠C=∠EDC,
∴DE=CE,
∴AB+BD=AE+CE=AC;
(2)延长AE、BC交于F,
∵AB=BF,BE平分∠ABF,
∴AE=EF,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(ASA),
∴AD=CF,
∴AB=BF=BC+CF=BC+AD.
【变式2-2】在“教、学、练、评一体化”学习活动手册中,全等三角形专题复习课,学习过七种作辅助线的方法,其中有“截长补短”作辅助线的方法.
截长法:在较长的线段上截取一条线段等于较短线段;
补短法:延长较短线段和较长线段相等.
这两种方法统称截长补短法.
请用这两种方法分别解决下列问题:
已知,如图,在△ABC中,AB>AC,∠1=∠2,P为AD上任一点,
求证:AB﹣AC>PB﹣PC.
【答案】证明见解答过程.
【解答】解:解法一:如图,在AB上截取AE,使AE=AC,连接PE,
在△AEP和△ACP中,
,
∴△AEP≌△ACP(SAS),
∴PE=PC,
在△PBE中,BE>PB﹣PE,
即AB﹣AC>PB﹣PC;
解法二:如图,延长AC到D,使AD=AB,连接PD,
在△ADP和△ABP中,
,
∴△ADP≌△ABP(SAS),
∴PD=PB,
在△PCD中,CD>PD﹣PC,
即AB﹣AC>PB﹣PC.
【变式2-3如图1,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)直接写出∠AFC的度数: 120° ;
(2)请你判断并写出FE与FD之间的数量关系;
(3)如图2,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,试判断线段AE、CD与AC之间的数量关系并说明理由.
【答案】见试题解答内容
【解答】(1)解:∵∠ACB=90°,∠B=60°,
∴∠BAC=90°﹣60°=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=15°,∠FCA=45°,
∴∠AFC=180°﹣(∠FAC+∠ACF)=120°
故答案为:120°;
(2)解:FE与FD之间的数量关系为:DF=EF.
理由:如图2,在AC上截取CG=CD,
∵CE是∠BCA的平分线,
∴∠DCF=∠GCF,
在△CFG和△CFD中,
,
∴△CFG≌△CFD(SAS),
∴DF=GF.
∵∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=∠BAC,∠FCA=∠ACB,且∠EAF=∠GAF,
∴∠FAC+∠FCA=(∠BAC+∠ACB)=(180°﹣∠B)=60°,
∴∠AFC=120°,
∴∠CFD=60°=∠CFG,
∴∠AFG=60°,
又∵∠AFE=∠CFD=60°,
∴∠AFE=∠AFG,
在△AFG和△AFE中,
,
∴△AFG≌△AFE(ASA),
∴EF=GF,
∴DF=EF;
(3)结论:AC=AE+CD.
理由:如图3,在AC上截取AG=AE,
同(2)可得,△EAF≌△GAF(SAS),
∴∠EFA=∠GFA.
又由题可知,∠FAC=∠BAC,∠FCA=∠ACB,
∴∠FAC+∠FCA=(∠BAC+∠ACB)=(180°﹣∠B)=60°,
∴∠AFC=180°﹣(∠FAC+∠FCA)=120°,
∴∠EFA=∠GFA=180°﹣120°=60°=∠DFC,
∴∠CFG=∠CFD=60°,
同(2)可得,△FDC≌△FGC(ASA),
∴CD=CG,
∴AC=AG+CG=AE+CD.
延长边上(不一定是底边)的中线,使所延长部分与中线相等,然后往往需要连接相应的顶点,则 对应角 对应边都对应相等。 此法常用于构造 全等三角形 ,利用中线的性质、 辅助线 、 对顶角 一般用“ SAS ”证明对应边之间的关系。 (在一定范围中)
截长:1.过某一点作长边的垂线;2.在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等。
补短:1.延长短边;2.通过旋转等方式使两短边拼合到一起
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题06 倍长中线法与截长补短法构造全等三形(两大类型)
重难点题型归纳
【题型一:倍长中线法构造全等三角形】
【题型二:截长补短法构造全等三角形】
【题型一:倍长中线法构造全等三角形】
△ABC中 , AD是BC边中线
方式1:直接倍长 延长AD到E,使DE=AD,连接BE
方式2:间接倍长
(1)作CF⊥AD于F,作BE⊥AD的延长线于E (2)延长MD到N,使DN=MD,连接CN
倍长中线法原理:
延长边上(不一定是底边)的中线,使所延长部分与中线相等,然后往往需要连接相应的顶点,则 对应角 对应边都对应相等。 此法常用于构造 全等三角形 ,利用中线的性质、 辅助线 、 对顶角 一般用“ SAS ”证明对应边之间的关系。(在一定范围中)
边上(不一定是底边)的中线,使所延长部分与中线相等,然后往往需要连接相
【典例1】为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小丽在组内做了如下尝试:如图1,在△ABC中,AD是BC边上的中线,延长AD到M,使DM=AD,连接BM.
【探究发现】:(1)图1中AC与BM的数量关系是 ,位置关系是 ;
【初步应用】:(2)如图2,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.(提示:不等式的两边都乘或除以同一个正数,不等号的方向不变.例如:若3x<6,则x<2.)
【探究提升】:(3)如图3,AD是△ABC的中线,过点A分别向外作AE⊥AB、AF⊥AC,使得AE=AB,AF=AC,延长DA交EF于点P,判断线段EF与AD的数量关系和位置关系,请说明理由.
【变式1-1】如图,已知AD是△ABC中BC边上的中线,AB=5,AC=3,则AD的取值范围是( )
A.2<AD<8 B.1<AD<4 C.2<AD<5 D.4≤AD≤8
【变式1-3】如图所示,AD为△ABC中线,D为BC中点,AE=AB,AF=AC,连接EF,EF=2AD.若△AEF的面积为3,则△ADC的面积为 .
【变式1-4】如图所示,D是△ABC边BC的中点,E是AD上一点,满足AE=BD=DC,FA=FE.求∠ADC的度数.
【变式1-6】已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE.
【变式1-5】(1)在△ABC中,AB=5,AC=3,求BC边上的中线AD的取值范围.
(2)受到(1)启发,请你证明下面的问题:如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.求证:BE+CF>EF.
【变式1-8】【阅读理解】
课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB的理由是 .
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是 .
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
【感悟】
解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
(3)如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC=BF.
【变式1-11】如图1,在△ABC中,AB=AC,D、E在BC边上,连接AD、AE,AD=AE;
(1)求证:BD=CE;
(2)如图2,F为AE上一点,连接DF、CF,若DF=CF,∠DAE=60°,求证:AF=CE.
(3)如图3,在(2)的条件下,N为DE上一点,连接AN,∠BAD=2∠DAN,M为DF中点,连接AM,若AM=6,AF=5,求EN的长.
【变式1-12】阅读下面的题目及分析过程,并按要求进行证明.
已知:如图,点E是BC的中点,点A在DE上,且∠BAE=∠CDE.
求证:AB=CD.
分析:证明两条线段相等,常用的方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等,因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.
(1)现给出如下两种添加辅助线的方法,请任意选出其中一种,对原题进行证明.
①如图1,延长DE到点F,使EF=DE,连接BF;
②如图2,分别过点B、C作BF⊥DE,CG⊥DE,垂足分别为点F,G.
(2)请你在图3中添加不同于上述的辅助线,并对原题进行证明.
【变式1-13】(1)【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,在△ABC中,若AB=13,AC=9,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法,延长AD至点E,使DE=AD,连接BE,容易证得△ADC≌△EDB,再由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
(2)【初步运用】如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且∠FAE=∠AFE.若AE=4,EC=3,求线段BF的长.
(3)【拓展提升】如图3,在△ABC中,D为BC的中点,DE⊥DF分别交AB,AC于点E,F.求证:BE+CF>EF.
【变式1-16】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.其中一定成立是 (填序号).
【变式1-19】(1)阅读理解:
如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 ;
(2)问题解决:如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,以C为顶点作∠ECF,使得角的两边分别交AB,AD于E、F两点,连接EF,且EF=BE+DF,试探索∠ECF与∠A之间的数量关系,并加以证明.
【模型二:截长补短法构造全等三角形】
截长:1.过某一点作长边的垂线;2.在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等。
补短:1.延长短边;2.通过旋转等方式使两短边拼合到一起
【典例2】阅读下面材料:
小明遇到这样一个问题:
如图1,在△ABC中,AD平分∠BAC,∠ABC=2∠C.求证:AC=AB+BD;
小明通过思考发现,可以通过“截长、补短”两种方法解决问题:
方法一:如图2,在AC上截取AE,使得AE=AB,连接DE,可以得到全等三角形,进而解决问题.
方法二:如图3,延长AB到点E,使得BE=BD,连接DE,可以得到等腰三角形,进而解决问题.
(1)根据阅读材料,任选一种方法证明AC=AB+BD,根据自己的解题经验或参考小明的方法,解决下面的问题;
(2)如图4,四边形ABCD中,E是BC上一点,EA=ED,∠DCB=2∠B,∠DAE+∠B=90°,探究DC、CE、BE之间的数量关系,并证明.
【变式2-1】阅读:探究线段的和.差.倍.分关系是几何中常见的问题,解决此类问题通常会用截长法或补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明.
(1)请完成下题的证明过程:如图1,在△ABC中,∠B=2∠C,AD平分∠BAC.求证:AB+BD=AC.证明:在AC上截取AE=AB,连接DE
(2)如图2,AD∥BC,EA,EB分别平分∠DAB,∠CBA,CD过点E,求证:AB=AD+BC.
【变式2-2】在“教、学、练、评一体化”学习活动手册中,全等三角形专题复习课,学习过七种作辅助线的方法,其中有“截长补短”作辅助线的方法.
截长法:在较长的线段上截取一条线段等于较短线段;
补短法:延长较短线段和较长线段相等.
这两种方法统称截长补短法.
请用这两种方法分别解决下列问题:
已知,如图,在△ABC中,AB>AC,∠1=∠2,P为AD上任一点,
求证:AB﹣AC>PB﹣PC.
【变式2-3如图1,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)直接写出∠AFC的度数: ;
(2)请你判断并写出FE与FD之间的数量关系;
(3)如图2,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,试判断线段AE、CD与AC之间的数量关系并说明理由.
专题06 倍长中线法与截长补短法构造全等三形(两大类型)
重难点题型归纳
【题型一:倍长中线法构造全等三角形】
【题型二:截长补短法构造全等三角形】
【题型一:倍长中线法构造全等三角形】
△ABC中 , AD是BC边中线
方式1:直接倍长 延长AD到E,使DE=AD,连接BE
方式2:间接倍长
(1)作CF⊥AD于F,作BE⊥AD的延长线于E (2)延长MD到N,使DN=MD,连接CN
倍长中线法原理:
延长边上(不一定是底边)的中线,使所延长部分与中线相等,然后往往需要连接相
【典例1】为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小丽在组内做了如下尝试:如图1,在△ABC中,AD是BC边上的中线,延长AD到M,使DM=AD,连接BM.
【探究发现】:(1)图1中AC与BM的数量关系是 AC=BM ,位置关系是 AC∥BM ;
【初步应用】:(2)如图2,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.(提示:不等式的两边都乘或除以同一个正数,不等号的方向不变.例如:若3x<6,则x<2.)
【探究提升】:(3)如图3,AD是△ABC的中线,过点A分别向外作AE⊥AB、AF⊥AC,使得AE=AB,AF=AC,延长DA交EF于点P,判断线段EF与AD的数量关系和位置关系,请说明理由.
【答案】(1)AC=BM,AC∥BM;
(2)2<AD<10;
(3)EF=2AD,EF⊥AD,理由见解析.
【解答】解:(1)∵AD是△ABC的中线,
∴BD=CD,
在△ADC和△MDB中,
,
∴△ADC≌△MDB(SAS),
∴AC=BM,∠CAD=∠M,
∴AC∥BM,
故答案为:AC=BM,AC∥BM;
(2)如图2,延长AD到M,使DM=AD,连接BM,
由(1)可知,△MDB≌△ADC(SAS),
∴BM=AC=8,
在△ABM中,AB﹣BM<AM<AB+BM,
∴12﹣8<AM<12+8,
即4<2AD<20,
∴2<AD<10,
即BC边上的中线AD的取值范围为2<AD<10;
(3)EF=2AD,EF⊥AD,理由如下:
如图3,延长AD到M,使得DM=AD,连接BM,
由(1)可知,△BDM≌△CDA(SAS),
∴BM=AC,
∵AC=AF,
∴BM=AF,
由(2)可知,AC∥BM,
∴∠BAC+∠ABM=180°,
∵AE⊥AB、AF⊥AC,
∴∠BAE=∠FAC=90°,
∴∠BAC+∠EAF=180°,
∴∠ABM=∠EAF,
在△ABM和△EAF中,
,
∴△ABM≌△EAF(SAS),
∴AM=EF,∠BAM=∠E,
∵AD=DM,
∴AM=2AD,
∴EF=2AD,
∵∠EAM=∠BAM+∠BAE=∠E+∠APE,
∴∠APE=∠BAE=90°,
∴EF⊥AD.
【变式1-1】如图,已知AD是△ABC中BC边上的中线,AB=5,AC=3,则AD的取值范围是( )
A.2<AD<8 B.1<AD<4 C.2<AD<5 D.4≤AD≤8
【答案】B
【解答】解:如图,延长AD到E,使DE=AD,连接CE,
∵AD是BC边上的中线,
∴BD=CD,
在△ABD和△ECD中,
,
∴△ABD≌△ECD(SAS),
∴CE=AB=5,
在△ACE中,由三角形的三边关系得:CE﹣AC<AE<CE+AC,
∴5﹣3<AE<5+3,
即2<2AD<8,
∴1<AD<4,
故选:B.
【变式1-3】如图所示,AD为△ABC中线,D为BC中点,AE=AB,AF=AC,连接EF,EF=2AD.若△AEF的面积为3,则△ADC的面积为 1.5 .
【答案】1.5.
【解答】解:延长AD到点G,使DG=AD,连接BG,
∵D为BC中点,
∴△ADC的面积=△ADB的面积,BD=DC,
∵∠ADC=∠GDB,
∴△ADC≌△GDB(SAS),
∴△ADC的面积=△BDG的面积,BG=AC,
∵AC=AF,
∴BG=AF,
∵EF=2AD,AG=2AD,
∴EF=AG,
∵AE=AB,
∴△AEF≌△BGA(SSS),
∴△AEF的面积=△ABG的面积=3,
∴△ADC的面积=△BDG的面积=△ABD的面积=△ABG的面积=1.5,
故答案为:1.5.
【变式1-4】如图所示,D是△ABC边BC的中点,E是AD上一点,满足AE=BD=DC,FA=FE.求∠ADC的度数.
【答案】60°.
【解答】解:延长AD至G,使AD=DG,连接BG,在DG上截取DH=DC,
在△ADC和△GDB中,,
∴△ADC≌△GDB(SAS),
∴AC=BG,∠G=∠CAD,
∵FA=FE,
∴∠CAD=∠AEF,
∴∠G=∠CAD=∠AEF=∠BED,
∴BG=BE=AC,
∵AE=DC=BD,
∴AE+ED=DH+ED,
∴AD=EH,
在△DAC和△HEB中,
,
∴△DAC≌△HEB(SAS),
∴CD=BH,
∴BD=BH=DH,
∴△BDH为等边三角形,
∴∠C=∠BDH=60°=∠ADC.
故答案为:60°.
【变式1-6】已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE.
【答案】证明见解析.
【解答】证明:延长AE到F,使EF=AE,连接DF,
∵AE是△ABD的中线,
∴BE=ED,
在△ABE与△FDE中
,
∴△ABE≌△FDE(SAS),
∴AB=DF,∠BAE=∠EFD,
∵∠ADB是△ADC的外角,
∴∠DAC+∠ACD=∠ADB=∠BAD,
∴∠BAE+∠EAD=∠BAD,∠BAE=∠EFD,
∴∠EFD+∠EAD=∠DAC+∠ACD,
∴∠ADF=∠ADC,
∵AB=DC,∴DF=DC,
在△ADF与△ADC中
,
∴△ADF≌△ADC(SAS)
∴∠C=∠AFD=∠BAE.
【变式1-5】(1)在△ABC中,AB=5,AC=3,求BC边上的中线AD的取值范围.
(2)受到(1)启发,请你证明下面的问题:如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.求证:BE+CF>EF.
【答案】(1)1<AD<4;
(2)证明过程见解答.
【解答】解:(1)延长AD到点E,使DE=AD,连接BE,
∵AD是BC边的中线,
∴BD=DC,
∵∠ADC=∠BDE,
∴△ADC≌△EDB(SAS),
∴BE=AC=3,
在△ABC中,AB=5,
∴5﹣3<AE<5+3,
∴2<AE<8,
∴2<2AD<8,
∴1<AD<4;
(2)延长FD到点G,使GD=DF,连接BG,EG,
∵D是BC边上的中点,
∴BD=DC,
∵∠BDG=∠CDF,
∴△BDG≌△CDF(SAS),
∴BG=CF,
∵DE⊥DF,
∴ED是GF的垂直平分线,
∴EG=EF,
在△BEG中,BE+BG>EG,
∴BE+CF>EF.
【变式1-8】【阅读理解】
课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB的理由是 B .
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是 C .
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
【感悟】
解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
(3)如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC=BF.
【答案】见试题解答内容
【解答】(1)解:∵在△ADC和△EDB中
,
∴△ADC≌△EDB(SAS),
故选B;
(2)解:∵由(1)知:△ADC≌△EDB,
∴BE=AC=6,AE=2AD,
∵在△ABE中,AB=8,由三角形三边关系定理得:8﹣6<2AD<8+6,
∴1<AD<7,
故选C.
(3)证明:
延长AD到M,使AD=DM,连接BM,
∵AD是△ABC中线,
∴CD=BD,
∵在△ADC和△MDB中
∴△ADC≌△MDB,
∴BM=AC,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC,
即AC=BF.
【变式1-11】如图1,在△ABC中,AB=AC,D、E在BC边上,连接AD、AE,AD=AE;
(1)求证:BD=CE;
(2)如图2,F为AE上一点,连接DF、CF,若DF=CF,∠DAE=60°,求证:AF=CE.
(3)如图3,在(2)的条件下,N为DE上一点,连接AN,∠BAD=2∠DAN,M为DF中点,连接AM,若AM=6,AF=5,求EN的长.
【答案】(1)(2)证明见解析部分.
(3)7.
【解答】(1)证明:如图1中,过点A作AH⊥BC于点H.
∵AB=AC,AD=AE,AH⊥BC,
∴BH=CH,DH=EH,
∴BD=CE,
∴BD+DE=EC+DE,即BE=CD;
(2)证明:过点F作FT∥DE交AD于点T.
∵AD=AE,∠DAE=60°,
∴△ADE是等边三角形,
∴∠ADE=∠AED=60°,
∵FT∥DE,
∴∠ATF=∠ADE=60°,∠AFT=∠AED=60°,
∴△AFT是等边三角形,
∴AT=AF=FT,
∵AD=AE,
∴DT=EF,
∵FD=FC,
∴∠FDC=∠FCD=∠DFT,
∵∠DTF=∠CEF=120°,
∴△FTD≌△CEF(AAS),
∴FT=CE,
∴AF=EC;
(3)解:如图3中,延长AM到Q,使得MQ=AM,则AQ=2AM=12,设∠DAN=α,则∠BAD=∠CAE=2α.
∴∠B=60°﹣2α,
∴∠CNA=∠B+∠BAN=60°﹣2α+3α=60°+α,∠CAN=∠CAE+∠EAN=2α+60°﹣α=60°+α,
∴∠CNA=∠CAN,
∴CN=CA,
∵MA=MQ,∠AMF=∠QMD,MF=MD,
∴△MAF≌△MQD(SAS),
∴AF=DQ,∠MAF=∠Q,
∴DQ∥AE,
∴∠ADQ=180°﹣∠DAE=120°,
∵∠ADE=60°,
∴∠ADB=180°﹣∠ADE=120°,
∴∠ADB=∠ADQ=120°,
∵BD=EC=AF=5,
∴DB=DQ,
∵AD=AD,
∴△ADB≌△ADQ(SAS),
∴AB=AQ=12,
∴AC=AB=CN=12,
∴EN=12﹣5=7.
【变式1-12】阅读下面的题目及分析过程,并按要求进行证明.
已知:如图,点E是BC的中点,点A在DE上,且∠BAE=∠CDE.
求证:AB=CD.
分析:证明两条线段相等,常用的方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等,因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.
(1)现给出如下两种添加辅助线的方法,请任意选出其中一种,对原题进行证明.
①如图1,延长DE到点F,使EF=DE,连接BF;
②如图2,分别过点B、C作BF⊥DE,CG⊥DE,垂足分别为点F,G.
(2)请你在图3中添加不同于上述的辅助线,并对原题进行证明.
【答案】(1)(2)(3)证明见解答.
【解答】证明:(1)①如图1,延长DE到点F,使EF=DE,连接BF,
∵点E是BC的中点,
∴BE=CE,
在△BEF和△CED中,
,
∴△BEF≌△CED(SAS),
∴BF=CD,∠F=∠CDE,
∵∠BAE=∠CDE,
∴∠BAE=∠F,
∴AB=BF,
∴AB=CD;
②如图2,分别过点B、C作BF⊥DE,CG⊥DE,垂足分别为点F,G,
∴∠F=∠CGE=∠CGD=90°,
∵点E是BC的中点,
∴BE=CE,
在△BEF和△CEG中,
,
∴△BEF≌△CEG(AAS),
∴BF=CG,
在△BAF和△CDG中,
,
∴△BAF≌△CDG(AAS),
∴AB=CD;
(2)如图3,
过C点作CM∥AB,交DE的延长线于点M,
则∠BAE=∠EMC,
∵E是BC中点,
∴BE=CE,
在△BAE和△CME中,
,
∴△BAE≌△CME(AAS),
∴CM=AB,∠BAE=∠M,
∵∠BAE=∠EDC,
∴∠M=∠EDC,
∴CM=CD,
∴AB=CD.
【变式1-13】(1)【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,在△ABC中,若AB=13,AC=9,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法,延长AD至点E,使DE=AD,连接BE,容易证得△ADC≌△EDB,再由“三角形的三边关系”可求得AD的取值范围是 2<AD<11 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
(2)【初步运用】如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且∠FAE=∠AFE.若AE=4,EC=3,求线段BF的长.
(3)【拓展提升】如图3,在△ABC中,D为BC的中点,DE⊥DF分别交AB,AC于点E,F.求证:BE+CF>EF.
【答案】(1)2<AD<11;(2)7;(3)证明见解答.
【解答】(1)解:延长AD至点E,使DE=AD,连接BE,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
∴BE=AC=9,
∵AB﹣BE<AE<AB+BE,
∴4<AE<22
∴2<AD<11,
故答案为:2<AD<11.
(2)延长AD到M,使AD=DM,连接BM,如图2,
∵AD是△ABC中线,
∴BD=DC,
在△ADC和△MDB中,
,
∴△ADC≌△MDB(SAS),
∴BM=AC,∠CAD=∠M,
∵∠AFE=∠AEF,
∴AE=EF=4,
∴AC=AE+CE=7,
∴BM=AC=7,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC,
即AC=BF=7;
(3)证明:如图3,延长ED到点G,使GD=ED,连接CG、GF,
∵D是BC边上的中点,
∴CD=BD,
在△CDG和△BDE中,
,
∴△CDG≌△BDE(SAS),
∴CG=BE,
∵CG+CF>GF,
∴BE+CF>GF,
∵DE⊥DF,GD=ED,
∴DF垂直平分EG,
∴GF=EF,
∴BE+CF>EF.
【变式1-16】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.其中一定成立是 ①②④ (填序号).
【答案】见试题解答内容
【解答】解:(1)①延长FD到G,使得DG=DF,连接BG、EG.(或把△CFD绕点D逆时针旋转180°得到△BGD),
∴CF=BG,DF=DG,
∵DE⊥DF,
∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF.
②若∠A=90°,则∠EBC+∠FCB=90°,
由①知∠FCD=∠DBG,EF=EG,
∴∠EBC+∠DBG=90°,即∠EBG=90°,
∴在Rt△EBG中,BE2+BG2=EG2,
∴BE2+CF2=EF2;
(2):①∵F是AD的中点,
∴AF=FD,
∵在 ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF=∠BCD,故此选项正确;
②延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=EF=FM,故②正确;
③∵EF=FM,
∴S△EFC=S△CFM,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误;
④设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°﹣x,
∴∠EFC=180°﹣2x,
∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x,
∵∠AEF=90°﹣x,
∴∠DFE=3∠AEF,故此选项正确.
故答案为①②④.
【变式1-19】(1)阅读理解:
如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 1<AD<4 ;
(2)问题解决:如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,以C为顶点作∠ECF,使得角的两边分别交AB,AD于E、F两点,连接EF,且EF=BE+DF,试探索∠ECF与∠A之间的数量关系,并加以证明.
【答案】见试题解答内容
【解答】解:(1)阅读理解:
∵AD=DE,CD=BD,∠ADC=∠BDE,
∴△ADC≌△EDB(SAS)
∴AC=BE=3,
∵在△ABE中,AB﹣BE<AE<AB+BE
∴2<2AD<8,
∴1<AD<4,
故答案为:1<AD<4;
(2)问题解决:
解:(1)延长FD到G,使得DG=DF,连接BG、EG.
∵CD=DB,DF=DG,∠CDF=∠BDG,
∴△CDF≌△BDG(SAS)
∴CF=BG,
∵DE⊥DF,
∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF;
(3)问题拓展:∴∠A+2∠ECF=180°,
理由如下:延长AB至点N,使BN=DF,连接CN,
∵∠ABC+∠D=180°,∠ABC+∠CBN=180°,
∴∠D=∠CBN,且CD=CB,DF=BN,
∴△CDF≌△CBN(SAS)
∴CF=CN,
∵EF=BE+DF,
∴EF=BE+BN=EN,
在△CEF和△CEN中,
,
∴△CEF≌△CEN(SSS)
∴∠FCE=∠NCE=∠FCN=∠DCB,
∵∠ABC+∠D=180°,
∴∠A+2∠ECF=180°.
【模型二:截长补短法构造全等三角形】
【典例2】阅读下面材料:
小明遇到这样一个问题:
如图1,在△ABC中,AD平分∠BAC,∠ABC=2∠C.求证:AC=AB+BD;
小明通过思考发现,可以通过“截长、补短”两种方法解决问题:
方法一:如图2,在AC上截取AE,使得AE=AB,连接DE,可以得到全等三角形,进而解决问题.
方法二:如图3,延长AB到点E,使得BE=BD,连接DE,可以得到等腰三角形,进而解决问题.
(1)根据阅读材料,任选一种方法证明AC=AB+BD,根据自己的解题经验或参考小明的方法,解决下面的问题;
(2)如图4,四边形ABCD中,E是BC上一点,EA=ED,∠DCB=2∠B,∠DAE+∠B=90°,探究DC、CE、BE之间的数量关系,并证明.
【答案】见试题解答内容
【解答】(1)证明:方法一:∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△BAD和△EAD中
∴△ABD≌△AED(SAS)
∴BD=ED,∠AED=∠B=2∠C,
∵∠AED=∠C+∠EDC,
∴∠EDC=∠C,
∴ED=EC,
∴BD=EC,
∴AC=AB+BD;
(2)DC、CE、BE之间的数量关系是BE=DC+CE,
证明:在EB上截取EF,使得EF=DC,连接AF,
∵EA=ED,
∴∠EAD=∠EDA,
∴2∠DAE=180°﹣∠AED,
∵∠DAE+∠B=90°,
∴2∠DAE+2∠B=180°,
∴∠AED=2∠B=∠C,
∵∠BED=∠CDE+∠DAE,
∴∠AEB=∠CDE,
在△AEF和△EDC中
∴△AEF≌△EDC(SAS),
∴EC=AF∠AFE=∠C=2∠B,
∵∠AFE=∠B+∠BAF,
∴∠ABF=∠BAF,
∴BF=AF,
∴BF=CE,
∴BE=DC+CE.
【变式2-1】阅读:探究线段的和.差.倍.分关系是几何中常见的问题,解决此类问题通常会用截长法或补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明.
(1)请完成下题的证明过程:如图1,在△ABC中,∠B=2∠C,AD平分∠BAC.求证:AB+BD=AC.证明:在AC上截取AE=AB,连接DE
(2)如图2,AD∥BC,EA,EB分别平分∠DAB,∠CBA,CD过点E,求证:AB=AD+BC.
【答案】见试题解答内容
【解答】证明:在AC上截取AE=AB,连接DE,如图1:
∵AD平分∠BAC,
∴∠BAD=∠DAC,
在△ABD和△AED中,
,
∴△ABD≌△AED(SAS),
∴∠B=∠AED,BD=DE,又∠B=2∠C,
∴∠AED=2∠C,
而∠AED=∠C+∠EDC=2∠C,
∴∠C=∠EDC,
∴DE=CE,
∴AB+BD=AE+CE=AC;
(2)延长AE、BC交于F,
∵AB=BF,BE平分∠ABF,
∴AE=EF,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(ASA),
∴AD=CF,
∴AB=BF=BC+CF=BC+AD.
【变式2-2】在“教、学、练、评一体化”学习活动手册中,全等三角形专题复习课,学习过七种作辅助线的方法,其中有“截长补短”作辅助线的方法.
截长法:在较长的线段上截取一条线段等于较短线段;
补短法:延长较短线段和较长线段相等.
这两种方法统称截长补短法.
请用这两种方法分别解决下列问题:
已知,如图,在△ABC中,AB>AC,∠1=∠2,P为AD上任一点,
求证:AB﹣AC>PB﹣PC.
【答案】证明见解答过程.
【解答】解:解法一:如图,在AB上截取AE,使AE=AC,连接PE,
在△AEP和△ACP中,
,
∴△AEP≌△ACP(SAS),
∴PE=PC,
在△PBE中,BE>PB﹣PE,
即AB﹣AC>PB﹣PC;
解法二:如图,延长AC到D,使AD=AB,连接PD,
在△ADP和△ABP中,
,
∴△ADP≌△ABP(SAS),
∴PD=PB,
在△PCD中,CD>PD﹣PC,
即AB﹣AC>PB﹣PC.
【变式2-3如图1,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)直接写出∠AFC的度数: 120° ;
(2)请你判断并写出FE与FD之间的数量关系;
(3)如图2,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,试判断线段AE、CD与AC之间的数量关系并说明理由.
【答案】见试题解答内容
【解答】(1)解:∵∠ACB=90°,∠B=60°,
∴∠BAC=90°﹣60°=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=15°,∠FCA=45°,
∴∠AFC=180°﹣(∠FAC+∠ACF)=120°
故答案为:120°;
(2)解:FE与FD之间的数量关系为:DF=EF.
理由:如图2,在AC上截取CG=CD,
∵CE是∠BCA的平分线,
∴∠DCF=∠GCF,
在△CFG和△CFD中,
,
∴△CFG≌△CFD(SAS),
∴DF=GF.
∵∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=∠BAC,∠FCA=∠ACB,且∠EAF=∠GAF,
∴∠FAC+∠FCA=(∠BAC+∠ACB)=(180°﹣∠B)=60°,
∴∠AFC=120°,
∴∠CFD=60°=∠CFG,
∴∠AFG=60°,
又∵∠AFE=∠CFD=60°,
∴∠AFE=∠AFG,
在△AFG和△AFE中,
,
∴△AFG≌△AFE(ASA),
∴EF=GF,
∴DF=EF;
(3)结论:AC=AE+CD.
理由:如图3,在AC上截取AG=AE,
同(2)可得,△EAF≌△GAF(SAS),
∴∠EFA=∠GFA.
又由题可知,∠FAC=∠BAC,∠FCA=∠ACB,
∴∠FAC+∠FCA=(∠BAC+∠ACB)=(180°﹣∠B)=60°,
∴∠AFC=180°﹣(∠FAC+∠FCA)=120°,
∴∠EFA=∠GFA=180°﹣120°=60°=∠DFC,
∴∠CFG=∠CFD=60°,
同(2)可得,△FDC≌△FGC(ASA),
∴CD=CG,
∴AC=AG+CG=AE+CD.
延长边上(不一定是底边)的中线,使所延长部分与中线相等,然后往往需要连接相应的顶点,则 对应角 对应边都对应相等。 此法常用于构造 全等三角形 ,利用中线的性质、 辅助线 、 对顶角 一般用“ SAS ”证明对应边之间的关系。 (在一定范围中)
截长:1.过某一点作长边的垂线;2.在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等。
补短:1.延长短边;2.通过旋转等方式使两短边拼合到一起
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
