1.5.3 全等三角形的判定ASA、AAS 课件(21张PPT)
文档属性
| 名称 | 1.5.3 全等三角形的判定ASA、AAS 课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 20.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 09:04:51 | ||
图片预览




文档简介
(共21张PPT)
2023年秋季
三角形全等的判定
浙教版 八年级上
目录
第一:全等三角形的判定ASA
第二:全等三角形的判定AAS
第三:角平分线的性质定理
知识回顾
到目前为止,我们已学过哪些方法判定两三角形全等?
1. 全等三角形的定义
能够完全重合的两个三角形全等
三边对应相等的两个三角形全等
2.边边边公理(SSS)
3.边角边公理(SAS)
两边及其夹角对应相等的两个三角形全等
新课导入
思考:已知一个三角形的两个角和一条边,那么两个角与这条边的位置上有几种可能性呢?
A
B
C
A
B
C
图1
图2
在图1中, 边AB是∠A与∠B的夹边, 我们称这种位置关系为两角夹边
在图2中, 边BC是∠A的对边, 我们称这种位置关系为两角及其中一角的对边。
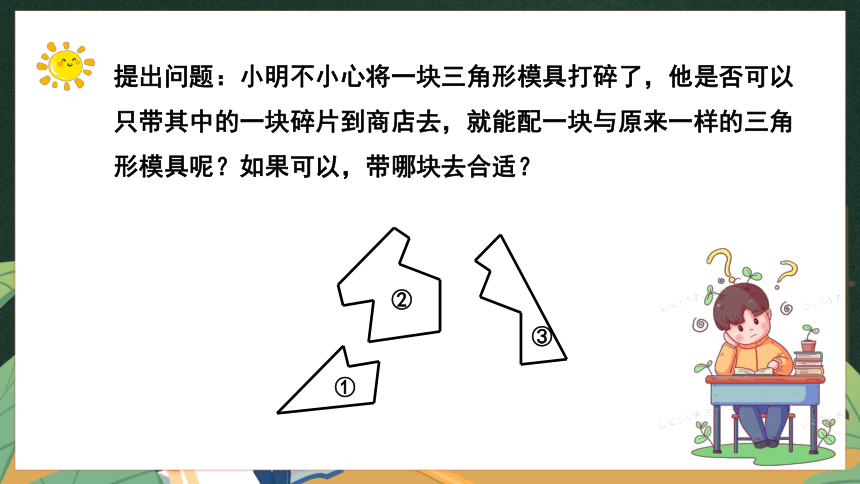
提出问题:小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?
①
②
③
C
B
A
600
400
3cm
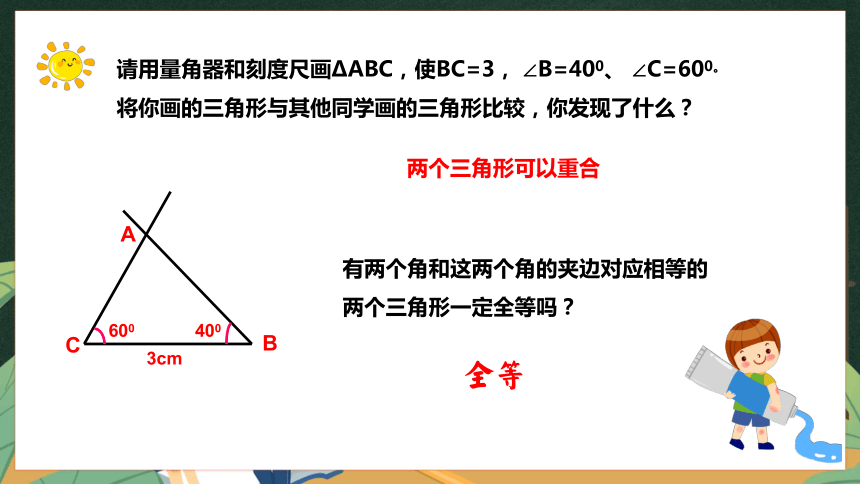
请用量角器和刻度尺画ΔABC,使BC=3, ∠B=400、 ∠C=600。 将你画的三角形与其他同学画的三角形比较,你发现了什么?
有两个角和这两个角的夹边对应相等的两个三角形一定全等吗?
两个三角形可以重合
全等
∴ΔABC≌ΔA B C (ASA)
在△ABC和△A B C 中
∠B=∠B
BC= B C
∠C=∠C
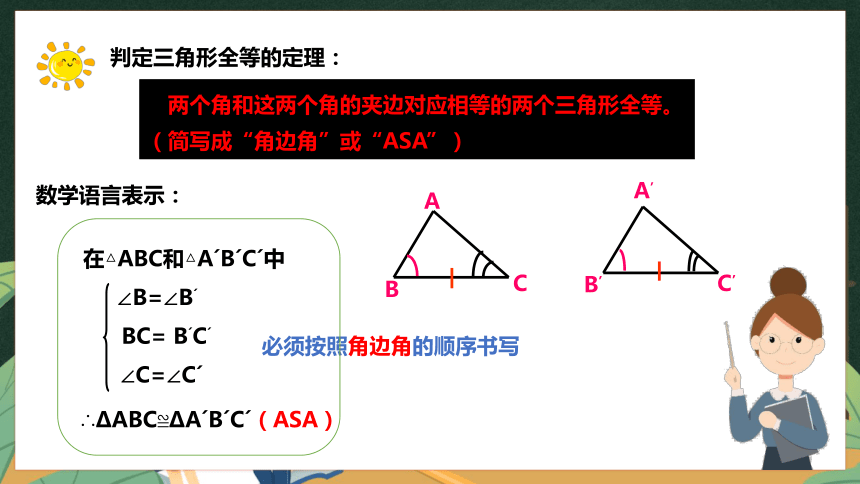
有两个角和这两个角的夹边对应相等的两个三角形全等。
(简写成“角边角”或“ASA”)
数学语言表示:
A
B
C
A’
B’
C’
必须按照角边角的顺序书写
判定三角形全等的定理:
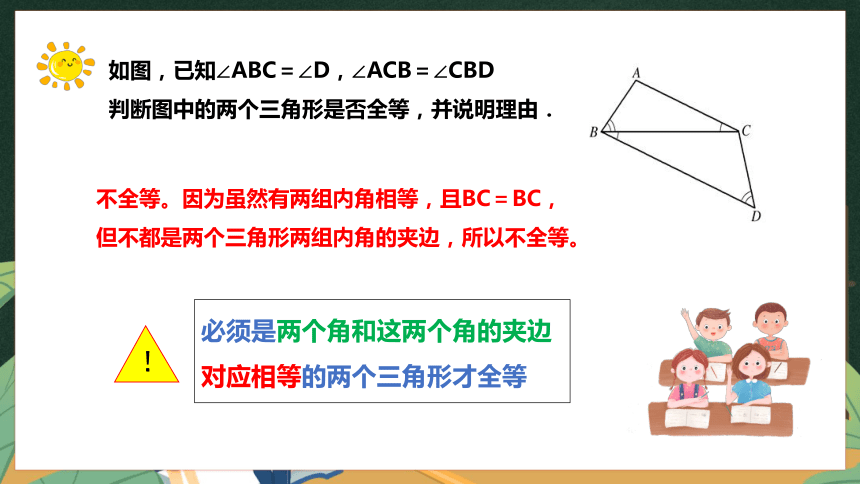
如图,已知∠ABC=∠D,∠ACB=∠CBD
判断图中的两个三角形是否全等,并说明理由.
不全等。因为虽然有两组内角相等,且BC=BC,但不都是两个三角形两组内角的夹边,所以不全等。
必须是两个角和这两个角的夹边对应相等的两个三角形才全等
!
例题讲解
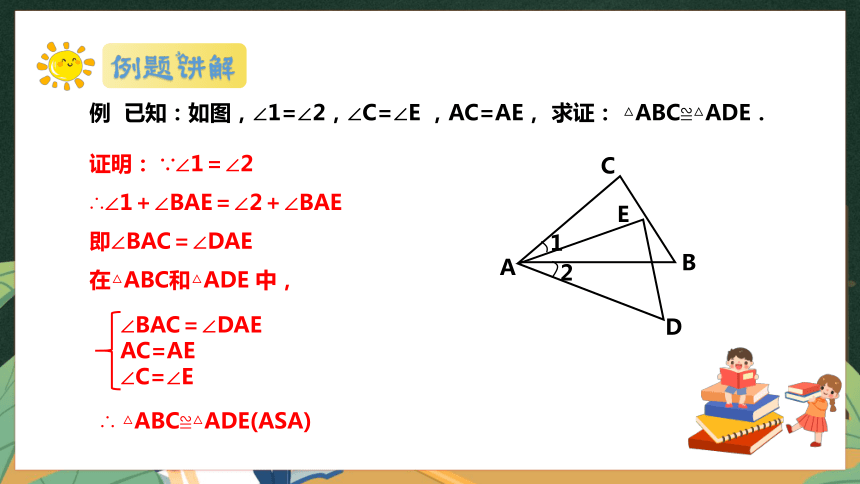
例 已知:如图,∠1=∠2,∠C=∠E ,AC=AE, 求证: △ABC≌△ADE.
证明: ∵∠1=∠2
∴∠1+∠BAE=∠2+∠BAE
即∠BAC=∠DAE
在△ABC和△ADE 中,
∴ △ABC≌△ADE(ASA)
A
C
B
E
D
1
2
∠BAC=∠DAE
AC=AE
∠C=∠E
提出问题:小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?
①
②
③
利用“角边角定理”可知,带③ 块去,可以配到一个与原来全等的三角形玻璃。
例 已知:如图,点B , F , E, C 在同一条直线上,AB∥CD,AB=CD,∠A= ∠ D.求证:AE=DF.
证明:∵ AB∥CD
∴ ∠B=∠C
在△ABE与△DCF中
∠A=∠D (已知)
AB=DC (已知)
∠B=∠C
∴ △ABE≌△DCF(ASA)
∴ AE=DF(全等三角形的对应边相等)
A
C
B
E
D
F
已知: 如图,点D,E分别在AC,AB上,∠B=∠C, AB=AC.
求证:AE=AD
A
B
D
E
C
证明:在△ABE与△ACD中,
∵ ∠A=∠A
AB=AC
∠B=∠C
∴△ACD≌△ABE(ASA),
∴AD=AE(全等三角形的对应边相等).
在△ABC和△DEF中, ∠A=∠D, ∠B=∠E,BC=EF, △ABC和△DEF全等吗?为什么?
A
C
B
E
D
F
分析:能否转化为ASA
证明:∵ ∠A=∠D, ∠B=∠E(已知)
∴∠C=∠F(三角形内角和定理)
∠B=∠E
在△ABC和△DEF中
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
你能从上题中得到什么结论?
两角及一角的对边对应相等的两个三角形全等
有两角及一角的对边对应相等的两个三角形全等 (简写成“角角边”或“AAS”)
判定三角形全等的定理:
A
B
C
D
E
F
数学语言表示:
在△ABC和△DEF中,
∵ ∠C=∠F
∠A=∠D,
AB=DE ,
∴ △ABC≌△DEF(AAS)
必须按照角角边的顺序书写
例题讲解
∴ △ APB ≌△APC(AAS)
∴ PB=PC(___________________________)
证明:
P
∵PB⊥AB,PC⊥AC(已知)
∴∠ABP=∠ACP=Rt∠(__________________)
在△APB与△APC中,
A
B
C
例.点P是∠BAC的平分线上的一点,PB⊥AB,PC⊥AC,求证:PB=PC
∠PAB=∠PAC(__________________)
∠ABP=∠ACP
AP=AP((公共边)
∵
全等三角形对应边相等
垂线的定义
角平分线的定义
角平分线上的点到角两边的距离相等。
角平分线的性质定理:
A
B
C
P
∵点P是∠BAC的平分线上的一点,
且PB⊥AB,PC⊥AC,
∴PB=PC(全等三角形对应边相等)
几何语言
例 如图,AB//CD,PB和PC平分∠ABC∠DCB,AD过点 P,且与 AB垂直。求证: PA=PD
证明:如图,作PE⊥BC于点E
∵ AB∥CD(已知)
∴∠BAD+∠CDA=180°(_____________________________)
∵AD⊥AB
∴∠BAD=90°
∴∠CDA=180°-∠BAD=180°-90°=90°
∴AD⊥CD(_____________________________________)
∵PB平分∠ABC
∴PA=PE ∴PA=PE=PD
两直线平行,同旁内角互补
角平分线上的点到角两边的距离相等
D
B
C
P
A
E
课堂练习
1. 通过学习我们已经知道三角形的三条内角平分线是交于一点的.如图,P是△ABC的内角平分线的交点,已知P点到AB边的距离为1,△ABC的周长为10,则△ABC的面积为______.
解: ∵P是△ABC的内角平分线的交点,
∴P到三边的距离相等,即到三边的距离都是1,
∴S△ABC=S△APC+S△APB+S△BPC
=×1×AC+×1×BC+×1×AB
=×1×(AC+BC+AB)
=×1×10=5.
所以△ABC的面积是5.
故填空答案:5.
5
2. 已知:如图,AD垂直平分BC , D为垂足. DM⊥AC, DN⊥AB, M,N分别为垂足. 求证:DM=DN.
A
B
C
D
M
N
解: ∵AD垂直平分BC,
∴AC=AB,CD=BD
∴∠C=∠B
∵DM⊥AC, DN⊥AB∴∠DMC=∠DNB=90°
∠DMC=∠DNB
∠C=∠B
CD=BD
∴ △DMC ≌△DNB(AAS)
∴ DM=DN
在△DMC与△DNB中,
总结归纳
SSS
SAS
ASA
AAS
两个三角形全等
的判定定理
谢谢观看
2023年秋季
三角形全等的判定
浙教版 八年级上
目录
第一:全等三角形的判定ASA
第二:全等三角形的判定AAS
第三:角平分线的性质定理
知识回顾
到目前为止,我们已学过哪些方法判定两三角形全等?
1. 全等三角形的定义
能够完全重合的两个三角形全等
三边对应相等的两个三角形全等
2.边边边公理(SSS)
3.边角边公理(SAS)
两边及其夹角对应相等的两个三角形全等
新课导入
思考:已知一个三角形的两个角和一条边,那么两个角与这条边的位置上有几种可能性呢?
A
B
C
A
B
C
图1
图2
在图1中, 边AB是∠A与∠B的夹边, 我们称这种位置关系为两角夹边
在图2中, 边BC是∠A的对边, 我们称这种位置关系为两角及其中一角的对边。
提出问题:小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?
①
②
③
C
B
A
600
400
3cm
请用量角器和刻度尺画ΔABC,使BC=3, ∠B=400、 ∠C=600。 将你画的三角形与其他同学画的三角形比较,你发现了什么?
有两个角和这两个角的夹边对应相等的两个三角形一定全等吗?
两个三角形可以重合
全等
∴ΔABC≌ΔA B C (ASA)
在△ABC和△A B C 中
∠B=∠B
BC= B C
∠C=∠C
有两个角和这两个角的夹边对应相等的两个三角形全等。
(简写成“角边角”或“ASA”)
数学语言表示:
A
B
C
A’
B’
C’
必须按照角边角的顺序书写
判定三角形全等的定理:
如图,已知∠ABC=∠D,∠ACB=∠CBD
判断图中的两个三角形是否全等,并说明理由.
不全等。因为虽然有两组内角相等,且BC=BC,但不都是两个三角形两组内角的夹边,所以不全等。
必须是两个角和这两个角的夹边对应相等的两个三角形才全等
!
例题讲解
例 已知:如图,∠1=∠2,∠C=∠E ,AC=AE, 求证: △ABC≌△ADE.
证明: ∵∠1=∠2
∴∠1+∠BAE=∠2+∠BAE
即∠BAC=∠DAE
在△ABC和△ADE 中,
∴ △ABC≌△ADE(ASA)
A
C
B
E
D
1
2
∠BAC=∠DAE
AC=AE
∠C=∠E
提出问题:小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?
①
②
③
利用“角边角定理”可知,带③ 块去,可以配到一个与原来全等的三角形玻璃。
例 已知:如图,点B , F , E, C 在同一条直线上,AB∥CD,AB=CD,∠A= ∠ D.求证:AE=DF.
证明:∵ AB∥CD
∴ ∠B=∠C
在△ABE与△DCF中
∠A=∠D (已知)
AB=DC (已知)
∠B=∠C
∴ △ABE≌△DCF(ASA)
∴ AE=DF(全等三角形的对应边相等)
A
C
B
E
D
F
已知: 如图,点D,E分别在AC,AB上,∠B=∠C, AB=AC.
求证:AE=AD
A
B
D
E
C
证明:在△ABE与△ACD中,
∵ ∠A=∠A
AB=AC
∠B=∠C
∴△ACD≌△ABE(ASA),
∴AD=AE(全等三角形的对应边相等).
在△ABC和△DEF中, ∠A=∠D, ∠B=∠E,BC=EF, △ABC和△DEF全等吗?为什么?
A
C
B
E
D
F
分析:能否转化为ASA
证明:∵ ∠A=∠D, ∠B=∠E(已知)
∴∠C=∠F(三角形内角和定理)
∠B=∠E
在△ABC和△DEF中
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
你能从上题中得到什么结论?
两角及一角的对边对应相等的两个三角形全等
有两角及一角的对边对应相等的两个三角形全等 (简写成“角角边”或“AAS”)
判定三角形全等的定理:
A
B
C
D
E
F
数学语言表示:
在△ABC和△DEF中,
∵ ∠C=∠F
∠A=∠D,
AB=DE ,
∴ △ABC≌△DEF(AAS)
必须按照角角边的顺序书写
例题讲解
∴ △ APB ≌△APC(AAS)
∴ PB=PC(___________________________)
证明:
P
∵PB⊥AB,PC⊥AC(已知)
∴∠ABP=∠ACP=Rt∠(__________________)
在△APB与△APC中,
A
B
C
例.点P是∠BAC的平分线上的一点,PB⊥AB,PC⊥AC,求证:PB=PC
∠PAB=∠PAC(__________________)
∠ABP=∠ACP
AP=AP((公共边)
∵
全等三角形对应边相等
垂线的定义
角平分线的定义
角平分线上的点到角两边的距离相等。
角平分线的性质定理:
A
B
C
P
∵点P是∠BAC的平分线上的一点,
且PB⊥AB,PC⊥AC,
∴PB=PC(全等三角形对应边相等)
几何语言
例 如图,AB//CD,PB和PC平分∠ABC∠DCB,AD过点 P,且与 AB垂直。求证: PA=PD
证明:如图,作PE⊥BC于点E
∵ AB∥CD(已知)
∴∠BAD+∠CDA=180°(_____________________________)
∵AD⊥AB
∴∠BAD=90°
∴∠CDA=180°-∠BAD=180°-90°=90°
∴AD⊥CD(_____________________________________)
∵PB平分∠ABC
∴PA=PE ∴PA=PE=PD
两直线平行,同旁内角互补
角平分线上的点到角两边的距离相等
D
B
C
P
A
E
课堂练习
1. 通过学习我们已经知道三角形的三条内角平分线是交于一点的.如图,P是△ABC的内角平分线的交点,已知P点到AB边的距离为1,△ABC的周长为10,则△ABC的面积为______.
解: ∵P是△ABC的内角平分线的交点,
∴P到三边的距离相等,即到三边的距离都是1,
∴S△ABC=S△APC+S△APB+S△BPC
=×1×AC+×1×BC+×1×AB
=×1×(AC+BC+AB)
=×1×10=5.
所以△ABC的面积是5.
故填空答案:5.
5
2. 已知:如图,AD垂直平分BC , D为垂足. DM⊥AC, DN⊥AB, M,N分别为垂足. 求证:DM=DN.
A
B
C
D
M
N
解: ∵AD垂直平分BC,
∴AC=AB,CD=BD
∴∠C=∠B
∵DM⊥AC, DN⊥AB∴∠DMC=∠DNB=90°
∠DMC=∠DNB
∠C=∠B
CD=BD
∴ △DMC ≌△DNB(AAS)
∴ DM=DN
在△DMC与△DNB中,
总结归纳
SSS
SAS
ASA
AAS
两个三角形全等
的判定定理
谢谢观看
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
