1.5.2 全等三角形的判定SAS 课件(21张PPT)
文档属性
| 名称 | 1.5.2 全等三角形的判定SAS 课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 20.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 09:07:33 | ||
图片预览




文档简介
(共21张PPT)
2023年秋季
三角形全等的判定
浙教版 八年级上
目录
第一:全等三角形的判定SAS
第二:全等三角形判定SAS的应用
第三:垂直平分线的定义
第四:垂直平分线的性质
知识回顾
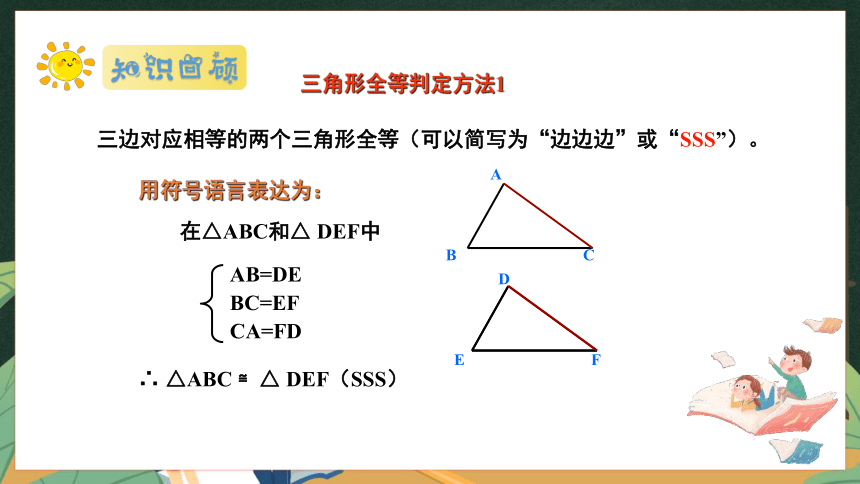
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
新课导入
如果满足三个条件画三角形,你能说出有哪几种可能的情况?
①三边;
②三角;
③两边一角;
④两角一边。
③两边一角;
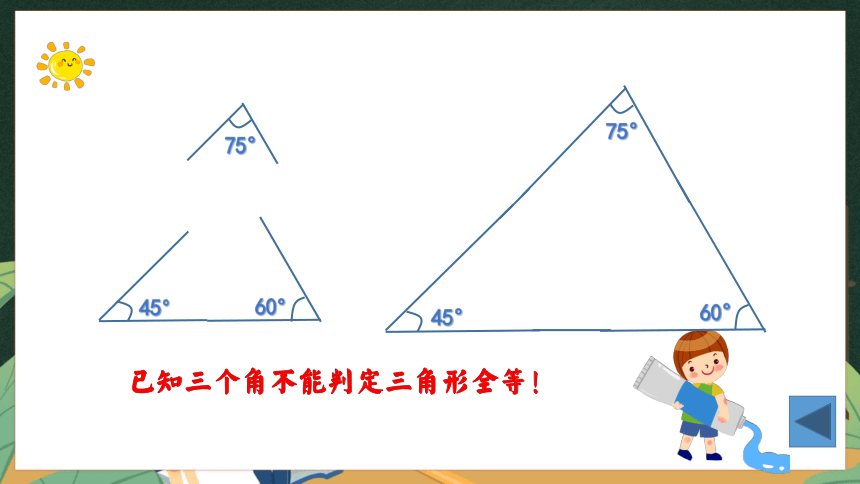
已知三个角不能判定三角形全等!
45°
45°
60°
60°
75°
75°
继续探讨三角形全等的条件:
两边一角
思考:已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
图一
图二
在图一中, ∠A是AB和AC的夹角,
符合图一的条件,它可称为“两边夹角”。
符合图二的条件, 通常说成“两边和其中一边的对角”
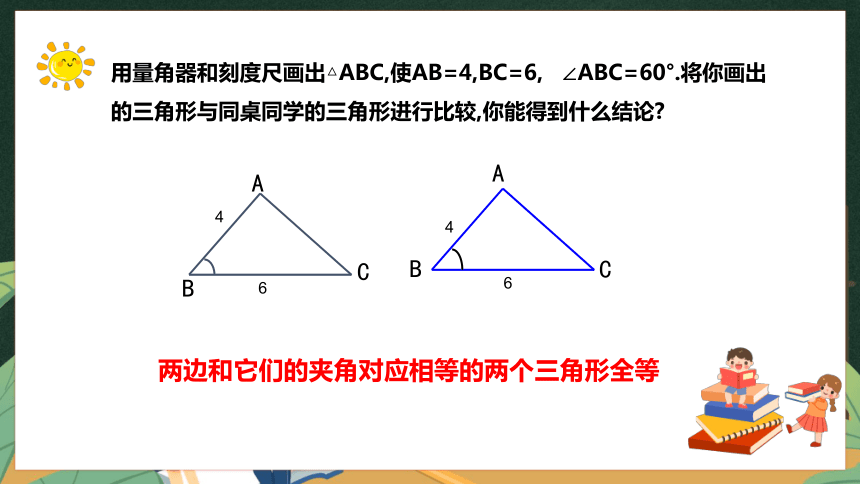
用量角器和刻度尺画出△ABC,使AB=4,BC=6, ∠ABC=60°.将你画出的三角形与同桌同学的三角形进行比较,你能得到什么结论
两边和它们的夹角对应相等的两个三角形全等
4
6
A
C
B
4
6
B
A
C
A
B
C
〃
\
A’
B’
C’
〃
\
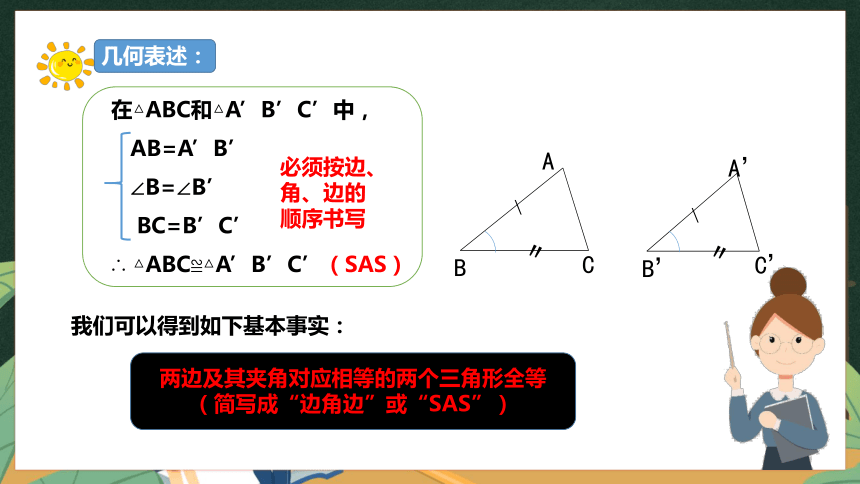
我们可以得到如下基本事实:
两边及其夹角对应相等的两个三角形全等
(简写成“边角边”或“SAS”)
在△ABC和△A’B’C’中,
AB=A’B’
∠B=∠B’
BC=B’C’
∴ △ABC≌△A’B’C’(SAS)
必须按边、角、边的顺序书写
几何表述:
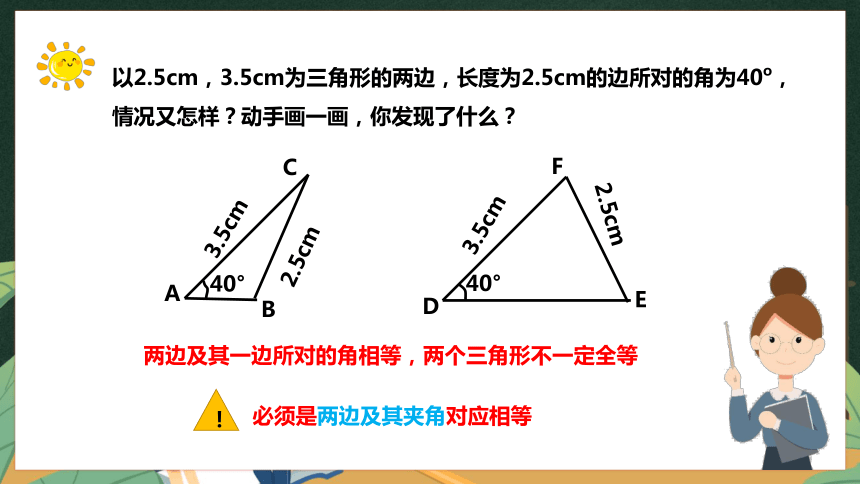
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40o,情况又怎样?动手画一画,你发现了什么?
A
B
C
2.5cm
3.5cm
40°
D
E
F
40°
3.5cm
2.5cm
两边及其一边所对的角相等,两个三角形不一定全等
!
必须是两边及其夹角对应相等
例题讲解
例 已知:如图,AC与BD相交于点O,且OA=OC,OB=OD
求证:△AOB≌△COD
A
B
O
D
C
证明:
在△AOB和△COD中,
OA=OC( )
∠AOB= ∠ COD ( )
OB=OD ( )
∴ △AOB≌△COD ( )
已知
已知
对顶角相等
SAS
∵
如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。说明卡钳的工作原理。
A
B
A′
B′
O
此工具是根据三角形全等制作而成的.
∵O是AA′,BB′的中点,∴AO=A′O,BO=B′O,
∴∠AOB=∠A′OB′(对顶角相等)
在△AOB和△A′OB′中,
∵ AO=A′O,
∠AOB=∠A′OB′,
BO=B′O,
∴△AOB≌△A′OB′(SAS),
∴A′B′=AB,
∴只要量出A′B′的长度,就可以测量工件内槽宽的卡钳
如图线段AB是一个池塘的长度,现在想测量这个池塘的长度,在水上测量不方便,你有什么好的方法较方便地把池塘的长度测量出来吗?想想看。
设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。
AC=DC
∠ACB=∠DCE
BC=EC
∴ △ACB≌△DCE(SAS)
∴ AB=DE
E
C
B
A
D
∵ 在△ACB和△DCE中,
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线。
A
B
D
l
∵ l⊥AB
AD=BD
∴ l是线段AB的垂直平分线
几何语言表述:
如图,直线l⊥AB于点D,且AD=BD,直线l 就是线段AB的垂直平分线。
在直线l上任意取一点C,用圆规比较点C到点A,B的距离,你发现了什么?
线段垂直平分线上的点到线段两端的距离相等
中垂线的性质:
∵ C是线段AB中垂线上一点
∴ CA=CB
A
B
O
l
C
证明“线段垂直平分线上的点到线段两端的距离相等”
已知:如图,直线l⊥AB于点O,且OA=OB。C是直线l上的任意一点。
求证:CA=CB
证明 已知OA=OB,当点C与点O为同一点,即重合时,显然CA=CB.
当点C与点O不重合时,∵直线l⊥AB(已知)
∴∠COA=∠COB=90°(垂直的定义)
A
B
O
l
C
在△CAO与△CBO中,
OA=OB(已知)
∠COA=∠COB,
OC=OC(公共边)
∴ △CAO≌△CBO(SAS)
∴ CA=CB(全等三角形的对应边相等)
课堂练习
①如图,点D、E分别在AC、AB上。已知AB=AC,AD=AE,求证:BD=CE。
证明:在ΔABD和 中,
AD = (已知)
= ( )
AB = AC( )
∴ ≌ ( )
∴ BD = CE( )
ΔACE
AE
∠A
∠A
已知
ΔABD
ΔACE
SAS
全等三角形的对应边相等
A
E
D
B
C
公共角
②. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.
A
B
C
D
E
③ 如图(2), △ABC中,DE垂直平分AC,AE=2cm, △ABD的周长是9cm,则△ABC的周长是_______.
A
B
C
D
E
13cm
10cm
④已知:如图,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED.求证:AC=CD.
A
B
C
D
E
解:证明:∵AB∥ED,
∴∠B=∠E.
在△ABC和△CED中,
AB=CE,
∠B=∠E,
BC=ED
∴△ABC≌△CED.
∴AC=CD.
如图,在△ABC中,∠ACB=90°,AC=BC,BD⊥CE,AE⊥CE,垂足分别为D、E,猜想图中线段DE、AE、DB之间的关系,并说明理由.
A
E
D
B
C
解:DE+AE=DB
∵∠ACB=90°,BD⊥CE
∴∠ACE+∠ECB=90°,
∠ECB+∠CBD=90°
∴∠ACE=∠CBD
又∵AE⊥CE
∴∠AEC=90°
在Rt△AEC和Rt△CDB中
AC=BC,∠AEC=∠CDB=90°,∠ACE=∠CBD
∴Rt△AEC≌Rt△CDB
∴AE=CD,EC=DB
又∵DE+DC=EC
∴DE+AE=DB.
总结归纳
(1)本节课学习了哪些主要内容?
(2)我们是怎么探究出“SAS”判定方法的?用
“SAS”判定三角形全等应注意什么问题?
(3)垂直平分线的性质是什么?
(4)到现在为止,你学到了几种证明两个三角形
全等的方法?
谢谢观看
2023年秋季
三角形全等的判定
浙教版 八年级上
目录
第一:全等三角形的判定SAS
第二:全等三角形判定SAS的应用
第三:垂直平分线的定义
第四:垂直平分线的性质
知识回顾
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
新课导入
如果满足三个条件画三角形,你能说出有哪几种可能的情况?
①三边;
②三角;
③两边一角;
④两角一边。
③两边一角;
已知三个角不能判定三角形全等!
45°
45°
60°
60°
75°
75°
继续探讨三角形全等的条件:
两边一角
思考:已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
图一
图二
在图一中, ∠A是AB和AC的夹角,
符合图一的条件,它可称为“两边夹角”。
符合图二的条件, 通常说成“两边和其中一边的对角”
用量角器和刻度尺画出△ABC,使AB=4,BC=6, ∠ABC=60°.将你画出的三角形与同桌同学的三角形进行比较,你能得到什么结论
两边和它们的夹角对应相等的两个三角形全等
4
6
A
C
B
4
6
B
A
C
A
B
C
〃
\
A’
B’
C’
〃
\
我们可以得到如下基本事实:
两边及其夹角对应相等的两个三角形全等
(简写成“边角边”或“SAS”)
在△ABC和△A’B’C’中,
AB=A’B’
∠B=∠B’
BC=B’C’
∴ △ABC≌△A’B’C’(SAS)
必须按边、角、边的顺序书写
几何表述:
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40o,情况又怎样?动手画一画,你发现了什么?
A
B
C
2.5cm
3.5cm
40°
D
E
F
40°
3.5cm
2.5cm
两边及其一边所对的角相等,两个三角形不一定全等
!
必须是两边及其夹角对应相等
例题讲解
例 已知:如图,AC与BD相交于点O,且OA=OC,OB=OD
求证:△AOB≌△COD
A
B
O
D
C
证明:
在△AOB和△COD中,
OA=OC( )
∠AOB= ∠ COD ( )
OB=OD ( )
∴ △AOB≌△COD ( )
已知
已知
对顶角相等
SAS
∵
如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。说明卡钳的工作原理。
A
B
A′
B′
O
此工具是根据三角形全等制作而成的.
∵O是AA′,BB′的中点,∴AO=A′O,BO=B′O,
∴∠AOB=∠A′OB′(对顶角相等)
在△AOB和△A′OB′中,
∵ AO=A′O,
∠AOB=∠A′OB′,
BO=B′O,
∴△AOB≌△A′OB′(SAS),
∴A′B′=AB,
∴只要量出A′B′的长度,就可以测量工件内槽宽的卡钳
如图线段AB是一个池塘的长度,现在想测量这个池塘的长度,在水上测量不方便,你有什么好的方法较方便地把池塘的长度测量出来吗?想想看。
设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。
AC=DC
∠ACB=∠DCE
BC=EC
∴ △ACB≌△DCE(SAS)
∴ AB=DE
E
C
B
A
D
∵ 在△ACB和△DCE中,
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线。
A
B
D
l
∵ l⊥AB
AD=BD
∴ l是线段AB的垂直平分线
几何语言表述:
如图,直线l⊥AB于点D,且AD=BD,直线l 就是线段AB的垂直平分线。
在直线l上任意取一点C,用圆规比较点C到点A,B的距离,你发现了什么?
线段垂直平分线上的点到线段两端的距离相等
中垂线的性质:
∵ C是线段AB中垂线上一点
∴ CA=CB
A
B
O
l
C
证明“线段垂直平分线上的点到线段两端的距离相等”
已知:如图,直线l⊥AB于点O,且OA=OB。C是直线l上的任意一点。
求证:CA=CB
证明 已知OA=OB,当点C与点O为同一点,即重合时,显然CA=CB.
当点C与点O不重合时,∵直线l⊥AB(已知)
∴∠COA=∠COB=90°(垂直的定义)
A
B
O
l
C
在△CAO与△CBO中,
OA=OB(已知)
∠COA=∠COB,
OC=OC(公共边)
∴ △CAO≌△CBO(SAS)
∴ CA=CB(全等三角形的对应边相等)
课堂练习
①如图,点D、E分别在AC、AB上。已知AB=AC,AD=AE,求证:BD=CE。
证明:在ΔABD和 中,
AD = (已知)
= ( )
AB = AC( )
∴ ≌ ( )
∴ BD = CE( )
ΔACE
AE
∠A
∠A
已知
ΔABD
ΔACE
SAS
全等三角形的对应边相等
A
E
D
B
C
公共角
②. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.
A
B
C
D
E
③ 如图(2), △ABC中,DE垂直平分AC,AE=2cm, △ABD的周长是9cm,则△ABC的周长是_______.
A
B
C
D
E
13cm
10cm
④已知:如图,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED.求证:AC=CD.
A
B
C
D
E
解:证明:∵AB∥ED,
∴∠B=∠E.
在△ABC和△CED中,
AB=CE,
∠B=∠E,
BC=ED
∴△ABC≌△CED.
∴AC=CD.
如图,在△ABC中,∠ACB=90°,AC=BC,BD⊥CE,AE⊥CE,垂足分别为D、E,猜想图中线段DE、AE、DB之间的关系,并说明理由.
A
E
D
B
C
解:DE+AE=DB
∵∠ACB=90°,BD⊥CE
∴∠ACE+∠ECB=90°,
∠ECB+∠CBD=90°
∴∠ACE=∠CBD
又∵AE⊥CE
∴∠AEC=90°
在Rt△AEC和Rt△CDB中
AC=BC,∠AEC=∠CDB=90°,∠ACE=∠CBD
∴Rt△AEC≌Rt△CDB
∴AE=CD,EC=DB
又∵DE+DC=EC
∴DE+AE=DB.
总结归纳
(1)本节课学习了哪些主要内容?
(2)我们是怎么探究出“SAS”判定方法的?用
“SAS”判定三角形全等应注意什么问题?
(3)垂直平分线的性质是什么?
(4)到现在为止,你学到了几种证明两个三角形
全等的方法?
谢谢观看
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
